Mrinal K Pal. Power system stability
Подождите немного. Документ загружается.


SMALL DISTURBANCE STABILITY
8-13
From (8.44), (8.46), (8.43) and (8.48) the state equation can be written as
∆
∆
∆
∆
=
∆
∆
∆
∆
exex
d
ex
x
Ψ
ω
δ
KGH
RBC
FK
I
x
Ψ
ω
δ
&
&
&
&
(8.49)
Note that most of the matrices and submatrices involved are block diagonal and sparse and this
can be taken advantage of in the computations.
The state model (8.49) is not unique. The state variables can be ordered in many other ways by
reordering the coefficient (
A) matrix accordingly.
State model for machine model 2
From (8.25) and (8.28)
[
]
δNYTMeTYTeZEZ ∆++∆=∆−∆
−−−
NNMM
111
from which
[]
[
]
[
]
δNYTMTTZTYTEZTTZTYTe ∆++−∆+=∆
−
−
−−−−
−
−−
NMNMMN
1
1
1111
1
11
(8.50)
Substituting (8.50) in (8.28)
δBEAi
∆
+
∆
=∆ (8.51)
where
[
]
11
1
1111 −−
−
−−−−
+−=
MMNMM
ZTTZTYTZZA
[]
[
]
NYTMTTZTYTZB
NMNM
++=
−
−
−−− 1
1
111
The linearized differential equations for the machine internal voltages, (8.10) and (8.11), can be
written in matrix form as
∆
∆
′
+
∆
∆
′
′
−
−
′
′
−
+
′
∆
′
∆
′
−
′
−
=
′
∆
′
∆
2
1
1
1
x
E
T
i
i
T
xx
T
xx
e
e
T
T
e
e
fd
do
q
d
do
dd
qo
qq
q
d
do
qo
q
d
&
&
As before, for
n machines the above can be written as
ex
xQiXEPE ∆+∆+∆=∆
&
which, using (8.51), becomes
ex
xQEDδCE ∆+∆+∆=∆
&
(8.52)
where
C = XB, D = P + XA
From (8.13) and (8.14), the linearized equations of motion for n machines can be written in
matrix form as
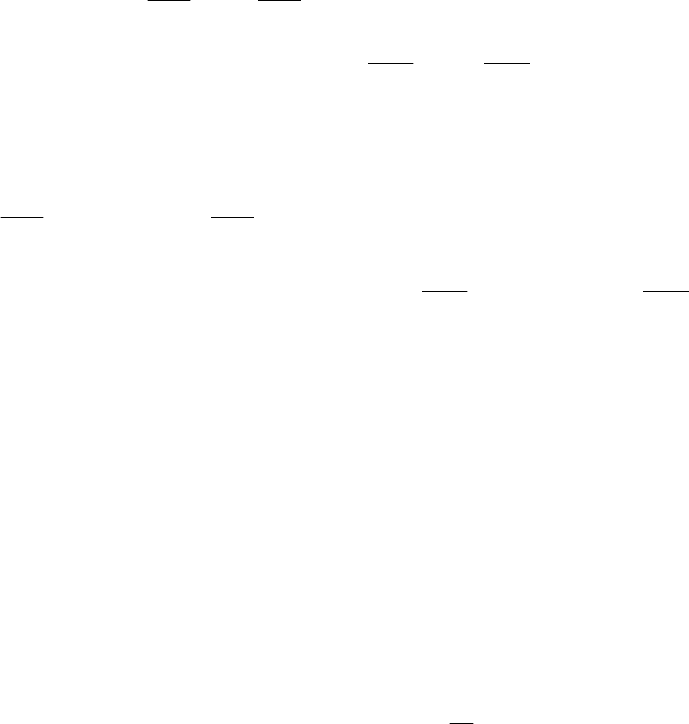
SMALL DISTURBANCE STABILITY
8-14
ωδ ∆=∆
&
(8.53)
ωKieEiω
∆
+
∆
+
∆
=∆
d
&
(8.54)
where
−−
−−
=
O
2
2
o
2
2
o
1
1
o
1
1
o
2H2H
2H2H
qd
qd
ii
ii
ωω
ωω
i
′
−
′
+
′
−
′
−
′
+
′
−
′
−
′
+
′
−
′
−
′
+
′
−
=
O
22
222
2
o
22
222
2
o
11
111
1
o
11
111
1
o
2H2H
2H2H
dd
dqq
qd
qqd
dd
dqq
qd
qqd
ix
ixe
ix
ixe
ix
ixe
ix
ixe
ωω
ωω
e
Using (8.51), (8.54) becomes
ωKδJEFω
∆
+
∆
+
∆
=∆
d
&
(8.55)
where
F = i + eA, J = eB
Excitation control equations (8.47) can be written as, using (8.50),
δHEGxKx
∆
+
∆
+
∆
=∆
exexex
&
(8.56)
where
[]
11
1
11 −−
−
−−
+=
MMN
ZTTZTYLTG
[]
[
]
NYTMTTZTYLTH
NMN
++−=
−
−
−− 1
1
11
From (8.53), (8.55), (8.52) and (8.56) the state model follows
∆
∆
∆
∆
=
∆
∆
∆
∆
exex
d
ex
x
E
ω
δ
KGH
QDC
FKJ
I
x
E
ω
δ
&
&
&
&
(8.57)
Mixed machine models
In multi-machine studies it is often desirable to employ different machine models to represent the
various machines in the system. For example, if one or several portions of the system are
represented by equivalent machines they may be represented by constant voltages behind
transient reactances, the so-called classical model, while the more detailed representations are

SMALL DISTURBANCE STABILITY
8-15
reserved only for the machines whose dynamic characteristics are desired to be accurately
evaluated. Also, in a system there may be a number of large induction motors which may greatly
affect the dynamic characteristics of the system and hence a detailed representation of these may
be desirable.
For the purpose of illustration the formation of the coefficient matrix for a system where some of
the synchronous machines are represented by model 2 and the rest by classical model will be
considered. It will however be clear that any combination of machine and control system
representation can similarly be handled.
The equations for the classical model can be written in the 2-axis representation as
ddqqq
qddd
ixiree
ixire
′
−−
′
=
′
+
−
=
where
q
e
′
is the constant voltage behind transient reactance
d
x
′
. This voltage being constant there
will be no differential equation to represent variation of flux linkages.
After linearization, the voltage equations can be written in matrix form, for
n machines, as
eiZE
∆
+
∆
=∆
M
(8.58)
where
E∆ is a null vector.
For the complete system (8.28) and (8.58) are written as one matrix equation before forming
(8.51).
The expression for the electrical torque is
qqe
ieT
′
=
which after linearization becomes
qqe
ieT
∆
′
=
∆
Therefore the linearized equation of motion for the machines employing the classical model, in
matrix form
ωKieω
∆
+
∆
=
∆
d
&
(8.59)
where
′
−
′
−
=
O
2
2
o
1
1
o
2
0
2
0
q
q
e
H
e
H
ω
ω
e
For the complete system, equations (8.54) and (8.59) are written as one matrix equation of the
form of (8.54), the matrix
i being augmented with the appropriate number of zeros, while the
new
e matrix is given by
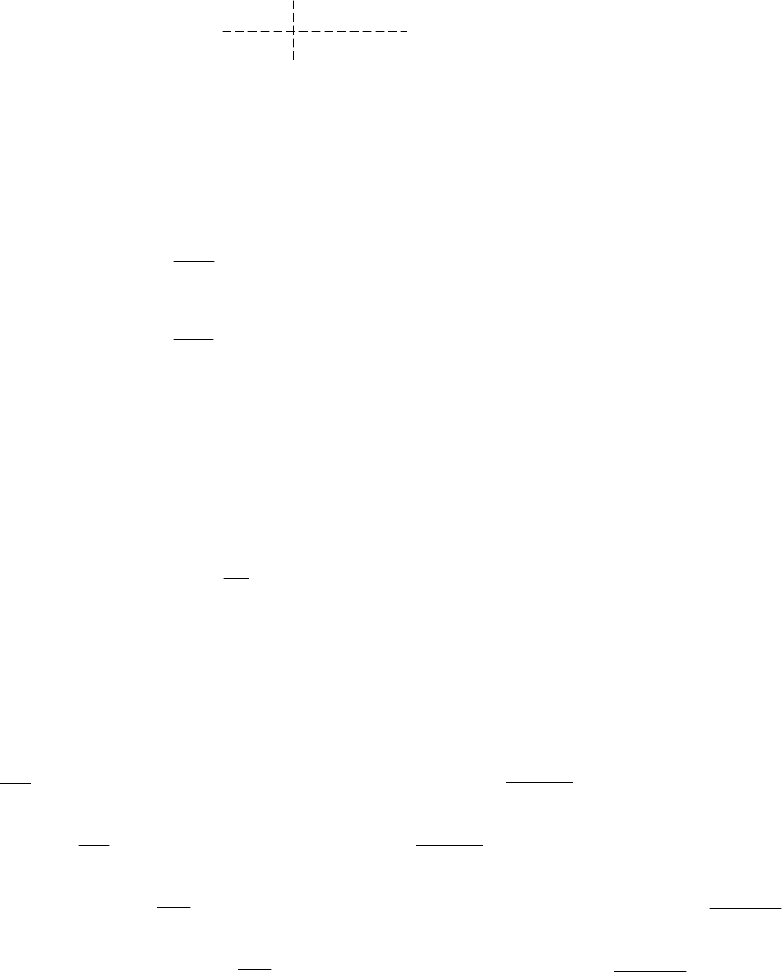
SMALL DISTURBANCE STABILITY
8-16
=
model classical
2 model
e
e
e
As before, by eliminating ∆
i the equation reduces to that given by (8.55).
State model for systems containing induction motor loads
The equations for the induction motor are given in Chapter 7 and reproduced here for
convenience.
QoQD
D
o
esTixxe
dt
ed
T
′′
+
′
−+
′
−=
′
′
o
)(
ω
(8.60)
DoDQ
Q
o
esTixxe
dt
ed
T
′′
−
′
−−
′
−=
′
′
o
)(
ω
(8.61)
QDQQ
DQDD
irixee
irixee
−
′
−
′
=
−
′
+
′
=
(8.62)
QQDDe
ieieT
′
+
′
= (8.63)
The equation of motion is
)(2
em
TT
dt
ds
H −−= (8.64)
The differential equations, for
n machines, can be linearized and written in matrix form as
sRiXEPE ∆+∆+∆=∆
&
(8.65)
where
′
−−
′
−
′
−−
′
−
=
O
2
2o
2o
2
1
1o
1o
1
1
1
1
1
o
o
o
o
T
s
s
T
T
s
s
T
ω
ω
ω
ω
P ,
′
′
−
−
′
′
−
′
′
−
−
′
′
−
=
O
2
22
2
22
1
11
1
11
o
o
o
o
T
xx
T
xx
T
xx
T
xx
X
′
−
′
′
−
′
=
O
2o
2o
1o
1o
D
Q
D
Q
e
e
e
e
ω
ω
ω
ω
R ,
∆
∆
=∆
M
2
1
s
s
s
The linearized equation of motion, assuming ∆
T
m
= 0, for n machines, in matrix form, is

SMALL DISTURBANCE STABILITY
8-17
Eiies
∆
+
∆
=∆
&
(8.66)
where
′
′
′
′
=
O
2
2
2
2
1
1
1
1
22
22
H
e
H
e
H
e
H
e
Q
D
Q
D
e ,
=
O
2
2
2
2
1
1
1
1
22
22
H
i
H
i
H
i
H
i
Q
D
Q
D
i
As before, the voltage equations in linearized form can be written as
eiZE
∆
+
∆
=
∆
M
(8.67)
where
′
′
−
′
′
−
=
O
22
22
11
11
rx
xr
rx
xr
M
Z
In the induction machine equations the axis voltages and currents are referred to a set of
synchronously rotating axes which can be assumed to coincide with the network reference axes.
Therefore, for the induction machines the transformation matrix
T will be a unit matrix, and the
vector
δ∆
will be a null vector.
For the complete system (8.28), (8.58) and (8.67) are written as one matrix equation before
forming (8.51).
The differential equations for the internal voltages of all the synchronous and induction machines
can be collected and written in matrix form as
ex
xQsRiXEPE ∆+∆+∆+∆=∆
&
(8.68)
The new
P and X matrices for the mixed machine model will be given by
=
machines induction
machines ssynchronou
P
P
P
,
=
machines induction
machines ssynchronou
X
X
X
The matrix
R is augmented with appropriate number of zeros.
Substituting the expression for ∆
i from (8.51) and rearranging, (8.68) reduces to
ex
xQsREDδCE ∆+∆+∆+∆=∆
&
(8.69)
where
C = XA and D = P + XB

SMALL DISTURBANCE STABILITY
8-18
The equations of motion for all the synchronous and induction machines can be written as one
matrix equation of the form of equation (8.54) with appropriate modifications to the vectors and
matrices. The new
i and e matrices will be given by
=
machine induction
2 model machine syn.
model classical
for elements zero
i
i
i
=
machineinduction
classical machine syn.
2 model machine syn.
e
e
e
e
By eliminating ∆
i the desired equation of the form of (8.55) will be obtained. The coefficient
matrix can then be formed as shown in (8.57).
Singularity of the coefficient matrix
The coefficient matrix of a multimachine system is singular in the absence of an infinite bus and
when absolute values of the machine angles are considered -- the columns corresponding to the
∆
δ
’s will add up to zero -- resulting in a zero eigenvalue. This is because the system is actually
of order (
m × n − 1) and not m × n, where m is the number of state variables per machine,
assuming all the machines are represented similarly. The singularity can be avoided, if desired,
by expressing the angles of the machines with reference to a particular machine taken as a
reference, thus reducing the number of variables by one. This calls for a few minor changes in
the coefficient matrix. For example, taking the
nth machine as reference, the required changes
can be achieved by deleting the row and column corresponding to
∆
δ
n
and placing −1 in the
intersection of the rows corresponding to
∆
δ
i
’s (i = 1, 2, … , n−1) and the column corresponding
to
∆
ω
n
. Apart from eliminating the zero eigenvalue the nonzero eigenvalues will remain
unchanged regardless of which machine is taken as reference. This can be demonstrated by
applying the fundamental properties of determinants.
When an infinite bus is present and the machine angles are measured with reference to that bus,
the system will be of order
m × n and the original coefficient matrix will be non-singular.
Procedure for Small-Disturbance Stability Studies
In the state space method of small-disturbance stability analysis, one or more operating
conditions whose stability properties need to be investigated would be selected and the state
model would be derived following the method(s) discussed earlier. The eigenvalues and
eigenvectors would then be computed using a standard eigenvalue computing package. For
efficiency, these two steps could be combined into one computer program. Conclusion about
stability and system response can then be drawn from an analysis of the eigenvalues and
eigenvectors. The program can be readily adapted to evaluate small-disturbance stability limits
under given sets of assumptions, impact on small-disturbance performance in response to
changes in system and control parameters and network flow, and also to meet various other
objectives.
SMALL DISTURBANCE STABILITY
8-19
In the state space approach of small-disturbance stability analysis the whole power system is
represented by one linear vector matrix equation and hence the eigenvalues contain information
on the dynamic response of the whole set of system variables rather than a few in which we are
usually interested. Any change in the system dynamic performance due to a change in the system
parameter can only be assessed by a proper interpretation of the eigenvalues. A change in the
control parameter of a particular machine may have effects on other machines which may be
quite remote and this will be reflected in the eigenvalues. The method is thus invaluable in
identifying the unstable modes not apparent in time domain simulations, their sources and
possible fixes of the problem.
From the solution of the vector differential equation Axx
=
&
, as given in Chapter 2, it is clear
that for a stable system a real eigenvalue will give rise to an exponentially decaying non-
oscillatory term, the decay time constant being the reciprocal of the eigenvalue, whereas a pair of
complex conjugate eigenvalues will give rise to an oscillatory term having an angular frequency
equal to the imaginary part, the oscillation decaying exponentially with a time constant which is
the reciprocal of the real part. Thus in a linear dynamic system the eigenvalues correspond to the
natural modes of response. An eigenvalue with a small negative real part will indicate the
presence of a transient term which is slow to die out. However, the relative magnitude of that
term in a particular variable will depend on the particular element of the associated eigenvector.
In multi-machine systems, in general, some of the eigenvalues are more sensitive to variations of
control parameters and operating conditions than others. Since in the output the eigenvalues are
printed in descending order of magnitude, it is sometimes difficult to follow the locus of any
particular eigenvalue with these changes. However, the sensitivity of a particular eigenvalue with
respect to a parameter may be calculated, if desired.
Eigen-sensitivity Analysis
Eigenvalue sensitivity information can be useful in determining the impact of changes of system
and control parameters on system modes and, therefore, parameters that have the most influence
on system damping can be identified. The expressions of sensitivities of eigenvalue
λ
i
and
eigenvector
x
i
of the coefficient matrix A with respect to a system parameter
α
have been
derived in Appendix A, and are given by
ii
ii
i
xy
x
A
y
′
∂
∂
′
=
∂
∂
α
α
λ
and
∑
≠
=
=
∂
∂
n
ij
j
jij
i
1
x
x
µ
α
,
respectively, where
jjji
ij
ij
xy
x
A
y
′
−
∂
∂
′
=
)(
λλ
α
µ
and
y
i
is the ith eigenvector of the transpose of A.

SMALL DISTURBANCE STABILITY
8-20
An important advantage of the method of deriving the state model as described previously is that,
in the coefficient matrix the elements involving any particular system parameter can be easily
located. The partial derivatives of the coefficient matrix with respect to a system parameter as
required in the calculation of eigen-sensitivities can therefore be readily formed. For example, if
the sensitivity of the eigenvalue
λ
i
with respect to a parameter of the excitation control system,
say the excitation gain constant of the
ith machine, K
Ai
, is desired, it is easily seen that only the
matrices
K
ex
, G and H contain this parameter. The partial derivatives with respect to K
Ai
of all
the other submatrices forming the final
A matrix will be null matrices. The derivative of K
ex
can
be easily formed by inspection. The derivatives of
G and H for the machine model 2 can be seen
to be
[
]
11
1
11 −−
−
−−
+
∂
∂
=
∂
∂
MMN
AiAi
KK
ZTTZTYT
LG
and
[
]
[
]
NYTMTTZTYT
LH
NMN
AiAi
KK
++
∂
∂
−=
∂
∂
−
−
−− 1
1
11
Since of the submatrices of which
G and H are formed only L contains K
Ai
.
System Performance
One advantage of formulating the power system small-disturbance problem in terms of state
variables is that many of the results from control theory can be applied. The general form of the
state space model consists of the pair of equations (see Chapter 2)
BuAxx
+
=
&
(8.70)
DuCxy
+
=
(8.71)
Note: In the discussion of small-disturbance stability through a state space approach presented
earlier in the chapter, the second term of the right hand side of equation (8.70) was absent. This
was due to the fact that the control vector was either constant or expressed beforehand in terms
of the state variables in which case the two terms on the right hand side of equation (8.70) were
combined together.
If the system is unstable or the eigenvalues are such that satisfactory performance is not
expected, the system can be stabilized and the performance improved by employing feedback.
The input
u(t) can be chosen to be function of the state variables, so that u = −hx, where h is the
feedback matrix. The state equation (8.70) then becomes
[
]
xAxBhABhxAxx
1
=−=−=
&
(8.72)
By appropriate selection of the elements of
h, the system can be stabilized and performance
improved.
Most of the results available from control theory are, however, impractical for large systems
such as a realistically sized power system. These are therefore of academic interest only,
although interesting applications are possible in small systems. Two of these are briefly
discussed here.
The first one uses the concepts of optimal control. The linearized equations, after dropping the
prefix
∆, are written in the form of (8.70). A quadratic performance index of the form
SMALL DISTURBANCE STABILITY
8-21
()
dtJ
T
∫
′
+
′
=
0
RuuQxx (8.73)
is then chosen and minimized. The elements of the positive definite matrices
Q and R are
selected after appropriate weighting which is usually guided by experience. The object of
minimizing
J is to minimize the sum of the error response and the control effort. It may be noted
that taking
Q as a unit matrix,
∫
′
T
dt
0
Qxx constitutes the familiar integral squared error criterion.
The methods as followed in deriving state models of the form of (8.3) can be used in deriving
equation (8.70) from a set of differential and algebraic equations. For example, equation (8.2)
will first be expressed as
u
B
B
y
x
AA
AA
0
x
+
=
2
1
43
21
&
(8.74)
where
u is the control vector.
From (8.74) (8.70) follows where
3
1
421
AAAAA
−
−= and
2
1
421
BAABB
−
−=
It is shown in standard texts on control theory that for optimal control (minimum
J) u is given by
KxBRu
′
−=
−1
(8.75)
where
K is a positive definite symmetric matrix satisfying the Riccati equation
0QKBKBRKAKA =−
′
+−
′
−
−1
(8.76)
Therefore the system (8.70) with optimal control reduces to
xAx
1
=
&
where
KBBRAA
′
−=
−11
Although the method is attractive it has to be limited to low order systems because of the
necessity of solving equations (8.76) to obtain the matrix
K.
Also, it can be seen from equation (8.75) that the optimal control is given by a linear
combination of all the state variables not all of which are directly measurable and available and
thus the real advantage of a rigorous theory may not be realized. This is so in a multi-machine
system where the optimal control law will suggest feedbacks of variables of one machine into
another. These, along with a less important fact that the optimal control law depends on the
choice of the matrices
Q and R in the expression for the performance index, do not render the
optimal control theory particularly useful in the design of the controls in a multi-machine system
in which power system engineers are more interested. As it stands it can be helpful only in the
design of controls in the relatively simple single machine-infinite bus systems.
A useful alternative, which is more suitable for small multi-machine systems, will be not to
establish the optimal control law in the way as described above, but to preselect the controls as
combinations of some of the measurable and available state variables which are likely to produce
SMALL DISTURBANCE STABILITY
8-22
improved dynamic response, then obtain an estimate of
∫
∞
′
0
dtQxx through the use of Liapunov
function and adjust the control parameters so as to reduce the numerical value of the integral.
Thus once again we start with equation
Axx
=
&
. To calculate the performance index given by
J =
∫
∞
′
0
dtQxx (8.77)
where
Q is a positive definite or semidefinite symmetric matrix, we make use of Liapunov’s
theorem on linear time-invariant systems.
Choosing a Liapunov function and its time derivative as
Pxxx
′
=
)(V (8.78)
Qxxx
′
−=)(V
&
(8.79)
where the positive definite symmetric matrix
P is determined from the equation
QPAPA
−
=
+
′
(8.80)
we have
∫∫
∞∞
−=
′
00
)(xQxx dVdt
For an asymptotically stable system
x(∝) = 0, and noting that V(0) = 0, we have
ooo
0
)( PxxxQxx
′
==
′
∫
∞
Vdt (8.81)
Thus the performance index is equal to the value of the Liapunov function
Pxx
′
at t = 0.
Solution of the equation QPAPA
−
=
+
′
Equation (8.80) has a unique solution for
P if 0
≠
+
ji
λ
λ
for all i, j, where
i
λ
are the
eigenvalues of the coefficient matrix
A. This condition will obviously be satisfied for an
asymptotically stable system. It is assumed that before trying to optimize a system performance
its stability has been properly checked.
To solve for the matrix
P we need to find the elements on and above (or below) the leading
diagonal of the matrix, which are given by the solution of the
n(n+1)/2 equations arising out of
the matrix equation (8.80). Although a direct solution is straightforward, the computation time
goes up considerably with the size of the system. For anything but the very small systems a
direct solution is not economical.
The computational burden can be reduced somewhat by first diagonalizing the matrix
A using
the relationship
ΛAMM =
−1
(see Appendix A), where Λ is a diagonal matrix composed of the
eigenvalues of
A (assuming the eigenvalues are distinct) and M is a square matrix whose
columns are the corresponding eigenvectors. Thus, we have
A = MΛM
−1
and MΛMA
′′
=
′
−
][
1
Using these relationships (8.80) reduces to
QPMΛMPMΛM −=+
′′
−− 11
][
