Mrinal K Pal. Power system stability
Подождите немного. Документ загружается.

SMALL DISTURBANCE STABILITY
8-23
Pre-multiplying and post-multiplying both sides by M′ and M, respectively, the above reduces to
SVΛΛV
−
=
+
(8.82)
where
QMMSPMMV
′
=
′
=
and
Equation (8.82) can be written in expanded form as
−=
++
++
++
MMM
L
L
L
MMM
L
L
L
332313
232212
131211
33323321331
23322221221
13311221111
2)()(
)(2)(
)()(2
sss
sss
sss
vvv
vvv
vvv
λλλλλ
λλλλλ
λλλλλ
The elements of
V can thus be easily calculated by equating the corresponding elements. Once V
is found,
P is calculated from
11
][
−−
′
= VMMP
Thus the performance index for various combinations of parameter values can be computed and
a selection of the parameter values for acceptable performance can be made. If desired, the
performance index can be minimized using a suitable function minimization technique.
Note that in the expression for the performance index (8.77) not all the state variables need to be
included. Also, the procedure can be readily adapted when the variables in the performance
index are chosen to be output (non-state) variables. For example, if we wish to estimate or
minimize
dtV
n
i
ti
∫
∑
∞
=
∆
0
1
2
, we note that from (8.17) eVV
∆
=
∆
t
and from (8.50) (assuming
machine model 2)
∆e = C∆x. Therefore the performance index becomes
∫∫∫∫
∑
∞∞∞∞
=
∆
′
∆=∆
′′′
∆=∆
′
∆=∆
0000
1
2
][][ dtdtdtdtV
tt
n
i
ti
xQxxVCVCxVV
which is of the same form as (8.77).
References
1. K. Ogata, State Space Analysis of Control Systems, Prentice-Hall, Inc. Englewood Cliffs, N.J. 1967.
2. M. Athans and P.L. Falb, Optimal Control, McGraw-Hill, N.Y. 1966.
3. R.C. Dorf, Modern Control Systems, Addison-Wesley Publishing Co. 1967.
4. M.K. Pal, “State Space Representation of Multi-Machine power Systems,” IEEE PES Summer Meeting &
Energy Resources Conf. Anaheim, CA, Paper C74 396-8, July 1974.
5. M.K. Pal, “Mathematical Methods in Power System Stability Studies,” Ph.D. Thesis, University of Aston in
Birmingham, 1972.

9-1
CHAPTER 9
TURBINE-GENERATOR SHAFT TORSIONALS
Most system disturbances, ranging from transmission line switching to electrical faults and
subsequent circuit breaker operations, produce transient oscillatory torques as well as step
changes in the torque level at the generator rotor air gap. These torques, whose magnitudes can
sometimes be several times the steady state level under full load condition, induce torsional
response in the turbine-generator shaft system. The resulting oscillations in the shaft system can
subject it to strain-cycles causing a loss of fatigue life. Since the shaft system generally has a
very low damping, oscillations once started can continue for a long time. At relatively high
oscillation amplitudes fatigue life expenditure can be considerable.
Under abnormal operating conditions the amount of stress the shaft system is subjected to would
depend on the nature of the disturbance, network parameters, system configuration, etc. Turbine-
generators are generally designed to withstand the effects of short circuits as required by industry
standards. Adequate margins are provided for carrying the steady state shaft torque at full load.
The highly oscillatory components of the transient electrical torque usually die out rapidly.
Occasionally, however, for example, when there is series capacitor in the transmission line, these
torques can be negatively damped due to self-excitation. There can also be resonance, when the
oscillation frequency coincides with one of the shaft system natural frequencies. Under these
conditions the shaft torque can build up and serious damage to the shaft system may result.
The generator electrical torque or the output power calculated in a conventional large scale
stability program does not contain the high frequency component. Computation of the high
frequency components requires a detailed machine representation which makes the computation
extremely time consuming. Also, the effect of the oscillations on the overall movement of the
rotor with respect to the system is not usually appreciable. For this reason, for conventional
stability calculations, it is adequate to employ a machine model (for example, one of the models
discussed in Chapter 5) that provides only the average torque. As an example, the electrical
torque or power following a three-phase terminal short circuit at no load, that would be obtained
from one of the synchronous machine models normally used in a conventional stability program,
is zero. The actual torque at the instant of short circuit is given by
t
x
V
T
d
t
e o
2
sin
ω
′′
≈
(9.1)
The above expression is arrived at by neglecting all resistances (stator and rotor), and assuming
qd
xx
′′
≈
′′
.
The fundamental frequency torque is caused by the dc offset of the transient current. It decays
rapidly -- approximately with the armature time constant. However, its initial value can be
several times the normal full load torque. The effect of stator and rotor resistances is to modify
the above expression somewhat and add additional terms which form the unidirectional
components. All these components decay at various stator and rotor time constants. For a
detailed discussion of the short circuit torques see Reference 3.
TURBINE-GENERATOR SHAFT TORSIONALS
9-2
Electrical torques generated due to other disturbances and switching operations are of a similar
nature. Under certain conditions the torques generated are in excess of that for a three-phase
terminal short circuit.
Problem
Show that the electrical torque due to synchronizing an unloaded generator, out of phase, against
an infinite bus, neglecting all resistances, subtransient saliency, voltage regulator and governor
actions, and assuming constant rotor speed and unity terminal and infinite bus voltage, is given
by
eded
e
xx
t
xx
T
+
′′
+
−
+
′′
≈
)
2
(cos
2
sin2
sin
o
δ
ω
δ
δ
(9.2)
where
δ
= angle by which the generator rotor leads the infinite bus
d
x
′′
= generator direct axis subtransient reactance
x
e
= reactance between generator terminal and infinite bus.
Note that the maximum value of the torque occurs when
δ
= 120°.
A Basic Analysis of the Shaft Torque Problem
In order to understand the effect of electrical system disturbances on the turbine-generator shaft
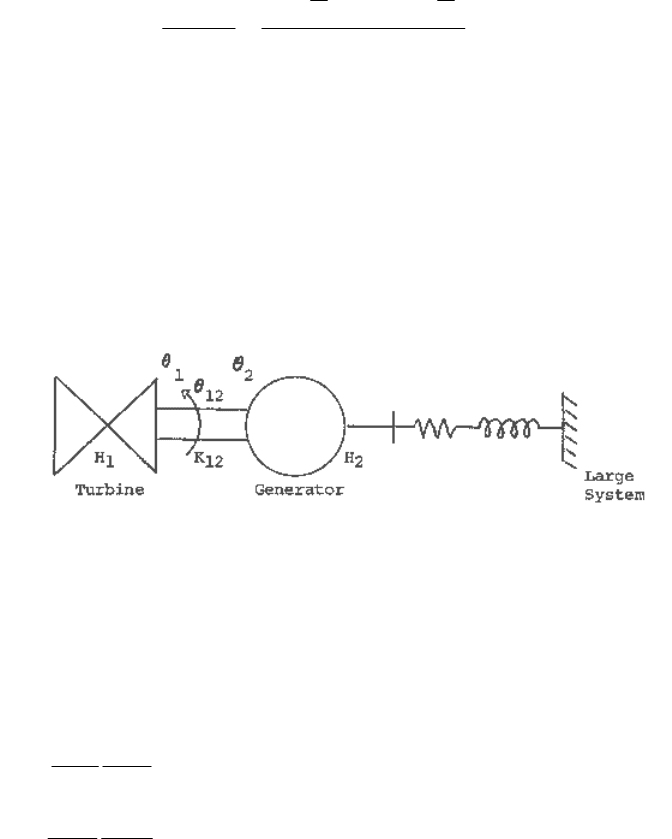
system consider the simple example shown in Figure 9.1
Fig.9.1 A simple turbine-generator torsional system.
In the absence of any interaction between the mechanical and the electrical system, the effect of
an electrical system disturbance can be analyzed by applying the change in the electrical torque
as a driving function to the equations of the mechanical system. The effect of interaction between
the mechanical and electrical system will be considered later.
The equations of motion of the turbine-generator shaft system can be written as
m
TKDD
dt
dH
=−++−+ )()(
2
2112112112
2
1
2
o
1
θθθθθ
θ
ω
&&&
(9.3)
)()(
2
2112221212
2
2
2
o
2
θθθθθ
θ
ω
−=++−+ KTDD
dt
dH
e
&&&
(9.4)
where
H
1
and H
2
are the inertias of the turbine and the generator rotor, respectively, T
m
is the
applied mechanical torque,
T
e
is the generator electrical torque, K
12
is the torsional stiffness of
the shaft,
D
1
and D
2
are the damping coefficients applicable to the turbine and the generator
TURBINE-GENERATOR SHAFT TORSIONALS
9-3
rotor, and D
12
is the damping coefficient to account for the damping arising within the shaft
material.
ω
o
= 2πf
o
, where f
o
is the electrical system frequency (60 Hz).
Assuming a constant applied mechanical torque, and
1221
DHDH
=
, for simplicity, (9.3) and
(9.4) can be linearized and combined as
e
T
HH
H
K
dt
d
D
dt
d
HH
HH
∆
+
=∆+∆+∆
+
21
1
1212121212
2
2
21o
21
)(
2
θθθ
ω
(9.5)
Assuming the disturbance torque
∆T
e
to be of the form )cos(
φωε
α
+
−
tT
t
, equation (9.5) can be
written as, writing
θ
for ∆
θ
12
for brevity,
)cos(2
2
2
2
φωεθω
θ
σ
θ
α
+=++
−
tA
dt
d
dt
d
t
n
(9.6)
where
21
21o12
2
21
21o12
2
)(
,
4
)(
HH
HHK
HH
HHD
n
+
=
+
=
ω
ω
ω
σ
and
2
o
2 H
T
A
ω
=
ω
n
corresponds to the natural frequency of the turbine-generator shaft system.
The general solution to equation (9.6) is of the form
[]
)cos(sincos
22
2
22
1
βφωεεσωσωθ
ασ
+++−+−=
−−
t
R
A
tCtC
tt
nn
(9.7)
where
222222
)(4)2(
σαωασαωω
−+−+−=
n
R (9.8)
and
ασαωω
σ
α
ω
β
2
)(2
tan
222
1
−+−
−
=
−
n
(9.9)
C
1
and C
2
are the two constants to be determined from the given initial conditions.
For example, for given initial values
o
θ
and
o
θ
&
, C
1
and C
2
are calculated as
)cos(
o1
βφθ
+−=
R
A
C
[]
+−+−−+
−
=
)sin()cos()(
1
oo
22
2
βφωβφασθσθ
σω
R
A
C
n
&
Therefore the complete solution can be written as

TURBINE-GENERATOR SHAFT TORSIONALS
9-4
[]
)cos(
sin)sin()cos()(
1
cos)cos(
sincos
22
22
22
22
22
oo
22
o
βφωε
εσωβφωβφασ
σω
σωβϕ
εσω
σω
θθσ
σωθθ
α
σ
σ
+++
−+−+−
−
+−+−
−
−
+
+−=
−
−
−
t
R
A
tt
R
A
tt
t
t
n
n
n
t
n
n
n
&
(9.10)
Note that the torque that the shaft will be subjected to is obtained by multiplying
θ
by the spring
constant
K
12
.
Equation (9.10) tells a great deal about the amount and type of stress the shaft system will be
subjected to under various electrical system disturbances.
The first two terms represent the free motion at shaft system natural frequency (
≈
ω
n
). These die
out at a rate determined by
σ
which is usually very small. The first term is due to the finite initial
values of
θ
and
θ
&
. For zero initial values, i.e., starting with no initial perturbation, this term will
be absent. Note that, depending on the initial perturbation, this term can greatly influence the
shaft movement and hence the stress level.
The third term represents the forced vibration due to the applied torque. It is at the same
frequency as that of the applied torque but displaced in phase. The initial magnitude of this (as
well as the second term) is dependent on the amplitude of the applied torque and the magnitude
of R given by (9.8).
Note that for a given shaft system the magnitude of
R depends largely on the frequency of the
applied torque. Depending on the nature of the disturbance, the applied torque may be composed
of one or more unidirectional and/or oscillatory components. For example, in a unit trip from full
load (full load rejection), the air-gap torque suddenly changes from full load value,
T
eo
, to zero.
Therefore, initially
∆T
e
= −T
eo
. In the case of other disturbances, ∆T
e
, in general, will have both
unidirectional and oscillatory components. The frequency of oscillation can range from inter-
machine swing frequency (1/2 - 2 Hz) to power frequency (60 Hz) and its second harmonic. All
these components generally decay rapidly with various time constants. Occasionally, however,
the decay rate can be very small and even negative.
Assuming
ω
n
to be in the 20 - 40 Hz range and assuming nominal decay rates for the applied
torques, approximate values of
R corresponding to the frequencies of interest can be estimated
from equation (9.8). It can be seen that
2
ω
≈R when the applied torque is at power frequency or
higher.
2
n
R
ω
≈ when the applied torque is unidirectional or at a low frequency, such as the inter-
machine swing frequency. When the frequency of the applied torque is close to
α
ω
ω
nn
R 2, ≈ .
Since
2
o
2
2
ωωαω
<<<<
nn
, we can conclude that the impact of an applied torque of a given
amplitude is greatest when its frequency is close to the shaft natural frequency (forming
resonance). Also, for low frequency or unidirectional applied torques, the impact is considerably
worse than that for torques at power frequency or higher.
TURBINE-GENERATOR SHAFT TORSIONALS
9-5
For most network disturbances
α
is large (which corresponds to short time-constants) and
therefore the third term of equation (9.10) decays very rapidly, although the initial peak can be
high if the applied torque has a high enough initial amplitude. However, the impact of the motion
imparted to the shaft system by the applied torque, as depicted by the second term of equation
(9.10), can be considerable, since it decays at a very slow rate due to the small value of
σ
.
The significance of the first term of equation (9.10) lies in fault clearing and high-speed
reclosing sometimes practiced as a means of improving stability limit. Any switching operation
is accompanied by transient oscillatory torque at the generator rotor air-gap. A system fault will
set the shaft system in motion, given by equation (9.10). If the system was in a steady state
before the fault, the first term in equation (9.10) will be absent. If the fault is cleared too soon,
before the forced vibration had sufficient time to decay, the initial perturbation for the transients
generated by fault clearance can be considerable. As a result the shaft system will be subjected to
a much higher stress level. The effect can be cumulative depending on the phase relationships of
the various terms, as can be seen from equation (9.10).
From the point of view of synchronous stability a fault clearing time faster than 3 cycles is
hardly worthwhile. During the first cycle or two, the unidirectional components of the electrical
torque due to the stator and rotor losses caused by the transient induced currents can be
substantial. The net accelerating torque immediately following a fault is therefore very small. It
can even be negative, causing the rotor to retard momentarily. Due to the modeling restriction,
the unidirectional component of the electrical torque is not fully accounted for in a conventional
large scale stability program. During the first three cycles into the fault the actual forward
movement of the rotor will therefore be very little. A faster clearing is therefore not likely to
improve system stability perceptively. However, as explained above, it can increase the stress on
the shaft system considerably.
A delayed clearing can also result in increased shaft torque and therefore should be avoided,
even if it is acceptable from system stability point of view. This is because, with delayed
clearing, the generator rotor would have advanced substantially by the time the fault is cleared.
The transient torque following fault clearing will therefore have a slowly varying component
with relatively high amplitude, and this will impart considerable shaft movement.
From equation (9.10), it can be seen that the actual torsional movement of the shaft depends on
various factors. At any instant of time, the deviation from the steady state position is determined
by the shaft system natural frequency, the frequency of the applied torque, various phase
relationships and damping. Most of these quantities will vary from one machine to another. Since
the shaft position and speed at the instant of fault clearing will serve as the initial conditions for
the transients following the fault clearing, the severity of these transients and the resulting shaft
stress would depend on the point on the transient wave at which the fault clearance takes place.
Since the actual wave shapes would be different for different machines, and cannot be predicted
exactly in advance, the best instant of fault clearing from shaft torsional point of view cannot be
determined. All things considered, the present practice of 3 - 3.5 cycles clearing appears to be the
most desirable.
Equation (9.10) also suggests the possibility of the shaft system being subjected to high stresses
following a fast reclosure. The third term in the equation will probably disappear by the time
reclosure takes place. However, the first two terms may still be significant due to the very low
damping within the shaft system. This, combined with the fact that there may be considerable
TURBINE-GENERATOR SHAFT TORSIONALS
9-6
angle difference between the generator rotor and the electrical system at the instant of reclosure
(c.f. the problem on synchronizing out of phase), could have the potential of causing even greater
stress on the shaft system. It may therefore be advisable to avoid fast reclosure unless it is really
necessary for maintaining stability. In those rare situations where fast reclosure is required, a
thorough analysis of the shaft system stresses should be performed.
Note that the possibility of closing into a fault (unsuccessful reclosure) presents a special hazard
in the practice of fast reclosure, especially if the fault is a three-phase short circuit close to the
machine terminal, since the transients following such unsuccessful reclosure and subsequent
clearing will be much more severe than normally encountered.
A great majority of system faults involve only one phase. Single phase clearing and reclosing in
such situations will not only improve system stability but also reduce shaft stresses considerably.
The cost of providing effective compensation for arc suppression, where required, has been
shown to be moderate. Therefore, a preferred alternative to three phase clearing and high speed
reclosing would be single pole switching. On those rare occasions when the fault is a close-in
three phase short circuit, fast reclosing can be blocked and alternative means of maintaining
system integrity can be resorted to.
Under certain circumstances the applied torque may be lightly damped or the damping may even
be negative, as a result of self-excitation due to the presence of series capacitors in the system.
The applied torque and consequently the shaft motion will then build up, as seen from equation
(9.10), when
α
is negative. Self-excitation will be considered in more detail later. Even when the
damping is positive, it could be small and the transient torque developed following a system
disturbance could have a frequency close to the torsional natural frequency of the shaft system.
The amplitude of the forced vibration can then reach a very high level, since
0→R at
n
ω
ω
=
for small values of
α
and
σ
as seen from equation (9.8). This is the familiar phenomenon of
resonance in forced vibration.
There can also be interaction between the shaft torsional system and the electrical system in the
presence of series capacitors, which could cause instability under conditions of resonance or near
resonance. Interaction between the shaft system and certain excitation and governor control
systems through the electrical system is also possible. This occurs when the speed signal utilized
in the control (in the case of excitation control, speed signal is used for power system
stabilization purposes) is derived at a shaft location which contains significant levels of torsional
natural frequency components. A method of simultaneously analyzing the effect of all these
interactions will be discussed later.
In the discussion of the torsional oscillation of the simple system shown in Figure 9.1, an
equation describing the relative motion of the turbine with respect to the generator rotor was
developed and solved. All the twisting was assumed to take place in the shaft. For analyses of
shaft stresses and torsional interactions with the electrical system this is permissible. The relative
motion of the turbine with respect to the generator, i.e., the twisting of the shaft is referred to as
the torsional mode. In conventional stability study the motion of the complete turbine-generator
system with respect to the electrical system (or other generators) is of interest. This is the
electrical system mode. Since the relative movement of the turbine with respect to the generator
rotor is small compared with the movement of the rotor with respect to the system, the torsional
mode can be neglected and the turbine-generator shaft system can be treated as a single rotating
mass in conventional stability studies.
TURBINE-GENERATOR SHAFT TORSIONALS
9-7
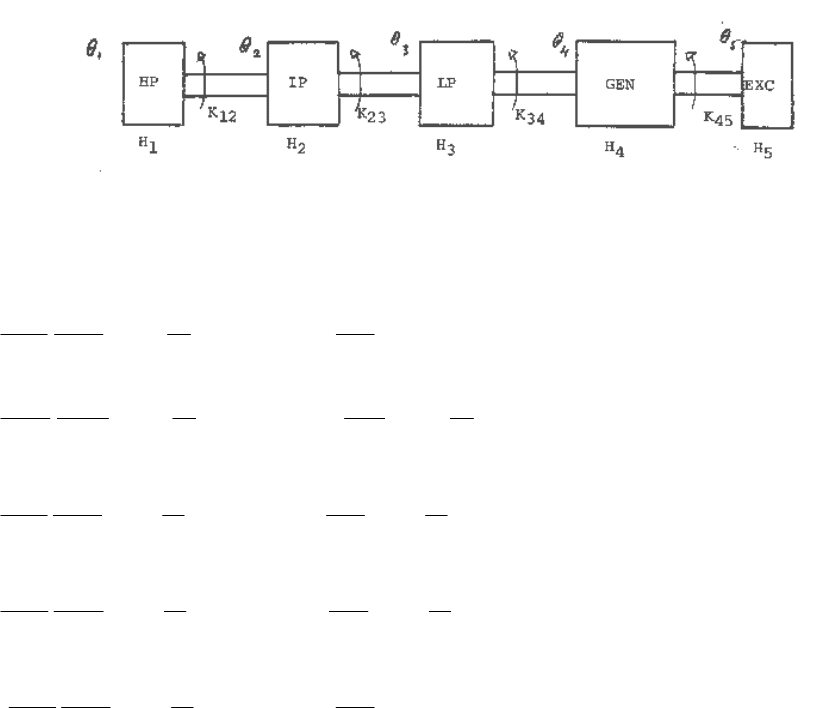
In the system of Figure 9.1 there is only one torsional mode. Generally, there will be more than
one turbine element, and there may also be a rotating exciter. The number of torsional modes in
such cases will be one less than the number of rotating elements.
Modes and Mode Shapes in a Turbine-Generator Shaft Torsional System
In the simple example considered so far there was only one torsional mode (or degree of
freedom), since there were only two rotating masses connected by a shaft. In a practical system
there will usually be more than one turbine section (such as high pressure, intermediate pressure,
low pressure, etc.), as well as the exciter connected to the generator rotor by a shaft. For analyses
of shaft torsional stresses at or below synchronous frequency (60 Hz), the turbine-generator
system can be represented by a spring-mass system, similar to that in the simple system, by
treating the various elements as point masses, assuming negligible twisting within the elements.
For example, a turbine generator with three turbine elements and an exciter can be represented as
in Figure 9.2.
Fig. 9.2 A turbine-generator shaft torsional model.
The equations of motion of the above system can be written, similar to those of the simple
system, as
12112
1
112112
2
1
2
o
1
)()(
2
m
TK
dt
d
D
dt
d
D
dt
dH
=−++−+
θθ
θ
θθ
θ
ω
(9.11)
2322312123223
2
221212
2
2
2
o
2
)()()()(
2
m
TKK
dt
d
D
dt
d
D
dt
d
D
dt
dH
=−+−+−++−+
θθθθθθ
θ
θθ
θ
ω
(9.12)
3433423234334
3
332323
2
3
2
o
3
)()()()(
2
m
TKK
dt
d
D
dt
d
D
dt
d
D
dt
dH
=−+−+−++−+
θθθθθθ
θ
θθ
θ
ω
(9.13)
e
TKK
dt
d
D
dt
d
D
dt
d
D
dt
dH
−=−+−+−++−+ )()()()(
2
544534345445
4
443434
2
4
2
o
4
θθθθθθ
θ
θθ
θ
ω
(9.14)
ex
TK
dt
d
D
dt
d
D
dt
dH
−=−++−+ )()(
2
4545
5
554545
2
5
2
o
5
θθ
θ
θθ
θ
ω
(9.15)
Since the shaft spring constants,
K
12
, etc., are large, )(
21
θ
θ
−
, etc. are small and can be assumed
to be zero, i.e.,
L
321
θ
θ
θ
≈≈ , when the motion of the whole turbine-generator shaft system
with respect to the electrical system or other generators is of interest, as in a conventional
stability study. With
L
321
θ
θ
θ
≈≈ , the above equations can be combined into

TURBINE-GENERATOR SHAFT TORSIONALS
9-8
me
TT
dt
d
D
dt
d
H
=++
δδ
ω
2
2
o
2
(9.16)
where
L
L
L
++=
++=
+
++=
2211
21
521
DDD
TTT
HHHH
mmm
)(
21
L≈≈≈
θ
θ
δ
is the angle with respect to the electrical system. T
ex
is small and can either be
neglected or included with
T
m
.
Equation (9.16) is the familiar swing equation used in convention stability studies.
Assuming constant mechanical torque and
T
ex
, equations (9.11) through (9.15) can be linearized
and written in matrix form as
TθK
θ
D
θ
H ∆=∆+
∆
+
∆
dt
d
dt
d
2
2
(9.17)
where
=
LLL
o
2
o
1
22
diag
ωω
HH
H
−++−
−++−
−+
=
LL
LLL
3434332323
2323221212
121211
DDDDD
DDDDD
DDD
D
−+−
−+−
−
=
LL
LLL
34342323
23231212
1212
KKKK
KKKK
KK
K
[]
′
∆∆∆=∆
521
θθθ
LLθ and
[]
′
∆=∆ 0000
e
TT
e
T∆ could be positive or negative; here it is assumed positive.
For an analysis of the torsional modes the damping terms can be neglected, since these are small.
Equation (9.17) can then be rearranged as
TAx
x
+=
2
2
dt
d
(9.18)
where
