Мостовской А.П. Информационные технологии в математике

Подождите немного. Документ загружается.

2.1 Примеры программирования в Математике 81

28. Do[Print[”x[”, i, ”] = ”, x[i]], {i, 1, ld, 1}]};

Пример. Введем в рабочем поле Математики три программы, при-

веденные в примерах 1,2 и 3 и запустим их в порядке следования. Пусть

m = {{1, 2, 1, 4}, {3, 4, 5, 6}, {5, 6, 7, 8}}

- матрица из коэффициентов и свободных членов линейной системы

трех уравнений относительно трех неизвестных. Решаем систему - вво-

дим команду common[m]. В результате получим две промежуточные

матрицы, треугольную матрицу системы и ответ.

2.1.5 Вычисление обратной матрицы методом Жордана

Следующая команда (вместе с r[w,i,j]) вычисляет обратную матрицу

методом Жордана с выводом на экран промежуточных результатов

вычисления.

common1[w

] := {w2 = w;

ld = Length[w2];

If[Det[w] == 0,

Print[”Нет обратной матрицы”]; Abort[],

Print[””]];

w1 = Transpose[Join[Transpose[w2], IdentityMatrix[ld]]];

Do[

Do[If[w1[[i + d − 1, d]]! = 0,

w1 = r[w1, d, i + d − 1];

w1 = w1/.w1[[d]]−> w1[[d]]/w1[[d, d]];

Do[If[kk! = d,

w1 = w1/.w1[[kk]]−> (w1[[kk]] − w1[[d]]w1[[kk, d]]), kk + +],

{kk, 1, ld}];

Print[d, ”Шаг : ”, w1//TraditionalForm], i + +],

{i, 1, ld − d + 1}],

{d, 1, ld}];

w3 = Transpose[Drop[Transpose[w1], ld]];

Print[” Ответ : ”,

N[w3, 5]//TraditionalForm]}[[1]];

Пример. Запустим программы 1 и 4 примеров. Введем, к примеру,

матрицу

m={{3,2,0,1},{2,-3,0,1},{3,4,-1,0},{-4,1,3,2}}

и выполним команду common1[m].

82 ГЛАВА 2. ПРОГРАММИРОВАНИЕ В МАТЕМАТИКЕ

2.1.6 Построение поверхности, заданной таблично

Построение поверхности, заданной таблично - своими значениями в

узлах прямоугольной решетки, может выполнить командой ListPlot3D.

Если решетка имеет другую форму, например, окружности, то можно

применить функцию непосредственного построения поверхности по уз-

лам

. Приведем пример построение поверхности, заданной таблично

над круговой решеткой.

Решетку можно задать командой вида

q = Union[Flatten[Table[{10t Sin[u], 10t Cos[u], 0},

{t, 0, 5}, {u, 0, 2π,

}], 1]]//N;

Команда Flatten[expr,1] убирает лишние скобки, а команда Union

- убирает дублирующие координаты. Выполните эти команды по от -

дельности для данного списка, чтобы убедится в правильности их ра-

боты.

Построим решетку.

qw = Graphics3D[Point/@q]

Show[qw, ViewPoint− > {2.819, 1.731, 0.713}]

Функцию в узлах такой решетки можно задать массивом точек ее

графика, расположенных над точками решетки. Рассмотрим для опре-

деленности следующую поверхность:

p = Table[{10tSin[u], 10tCos[u], 15 + t

+ u

{t, 0, 5}, {u, 0, 2π,

}]//N;

Построим точки графика этой поверхности. Выполним следующие

команды:

pq = Union[Flatten[Table[{10tSin[u], 10tCos[u],

15 + t

+ u

}, {t, 0, 5}, {u, 0, 2π,

}], 1]]//N;

qu = Graphics3D[Point/@pq]

Show[qw, qu, ViewPoint− > {2.865, 1.759, 0.379},

Boxed− > False]

Элемент списка p есть список координат точек лежащих над од-

ной окружностью или над центром окружности. Данный список надо

преобразовать в список вершин многоугольников (polygons), которые и

Функция взята из примера Tube в Help’е Mathematica 2.2.

2.1 Примеры программирования в Математике 83

порождают поверхность. Каждый такой многоугольник будет построен

командой Polygon. Поясним преобразование списка на простом приме-

ре.

Допустим, что список p имеет следующий простой вид

l = {{1, 2, 3}, {4, 5, 6}}

Здесь для простоты взята поверхность, заданная

всего шестью точками, причем, каждая тройка ко-

ординат одной точки графика обозначена цифрой.

Каждый элемент списка подвергнем циклическо-

му сдвигу влево

l1 = Map[RotateLeft, l] ⇒ {{2, 3, 1}, {5, 6, 4}}

и образуем список

num = {l, RotateLeft[l], RotateLeft[l1], l1} ⇒

{{{1, 2, 3}, {4, 5, 6}}, {{4, 5, 6}, {1, 2, 3}}, {{5, 6, 4}, {2, 3, 1}}, {{2, 3, 1}, {5, 6, 4}}}

Удалим в каждом элементе списка num последний элемент

num = Map[Drop[#, −1]&, num, {1}] ⇒

{{{1, 2, 3}}, {{4, 5, 6}}, {{5, 6, 4}}, {{2, 3, 1}}}

Удалим в каждом элементе второго уровня последний элемент

num = Map[Drop[#, −1]&, num, {2}] ⇒

{{{1, 2}}, {{4, 5}}, {{5, 6}}, {{2, 3}}}

Уберем лишние скобки

ee = Flatten[#, 1]&/@num ⇒

{{1, 2}, {4, 5}, {5, 6}, {2, 3}}

и полученный список-матрицу транспонируем

Transpose[ee] ⇒

{{1, 4, 5, 2}, {2, 5, 6, 3}}

Последние две команды можно объединить в одну

Transpose[Map[Flatten[#, 1]&, num]] ⇒

84 ГЛАВА 2. ПРОГРАММИРОВАНИЕ В МАТЕМАТИКЕ

{{1, 4, 5, 2}, {2, 5, 6, 3}}

Получился список вершин многоугольников из которых можно со-

ставить поверхность ”заданную ” списком l.

Объединим эти коман ды в одну функцию MakePolygon[vl_List]:

MakePolygon[vl List] :=

Block[{l = vl, l1 = Map[RotateLeft, vl], num},

num = {l, RotateLeft[l], RotateLeft[l1], l1};

num = Map[Drop[#, −1]&, num, {1}];

num = Map[Drop[#, −1]&, num, {2}];

{Polygon/@Transpose[Map[Flatten[#, 1]&, num]]}]

и построим поверхность следующей командой

Show[Graphics3D[MakePolygon[p]],

ViewPoint− > −2.710, 1.052, 1.732, Boxed− > False]

2.1.7 Симплекс-метод

Решим стандартную задачу линейного программирования, приме-

няя симплекс-метод. Такие задачи можно решить командами Minimize,

Maximize. Эти команды и им аналогичные приводят только ответ, не

выводя на экран промежуточные вычисления. Для вывода на экран

промежуточных этапов решения необходимо программирование, кото-

рое позволяет создать нужную команду. В этом параграфе создана ко-

манда simplex[a, b, c], которая выводит на экран все таблицы, возни-

кающие при решении задачи линейного программирования симплекс-

методом.

2.1 Примеры программирования в Математике 85

Надо найти максимум функции L(X) = c

+ c

+ ... + c

при

условии, что











+ a

+ ... + a

= b

+ a

+ ... + a

= b

· · ·

+ a

+ ... + a

= b

≥ 0, x

≥ 0, ..., x

≥ 0.

Будем рассматривать частный случай такой задачи, пусть матрица

коэффициентов системы имеет вид

a = {{3, 1, 5}, {4, 2, 5}, {6, 8, 2}};

столбец свободных членов

b = {60, 70, 41};

а коэффициенты при неизвестных в функции цели L(X)

c = {18, 17, 15};

Следующая вспомогательная функция выводит матрицу d в виде

прямоугольной таблицы, столбцы и строки которой разделены прямы-

ми линиями

hf[d

] := FrameBox[GridBox[d, RowLines− > {True},

ColumnLines− > True]]//DisplayForm

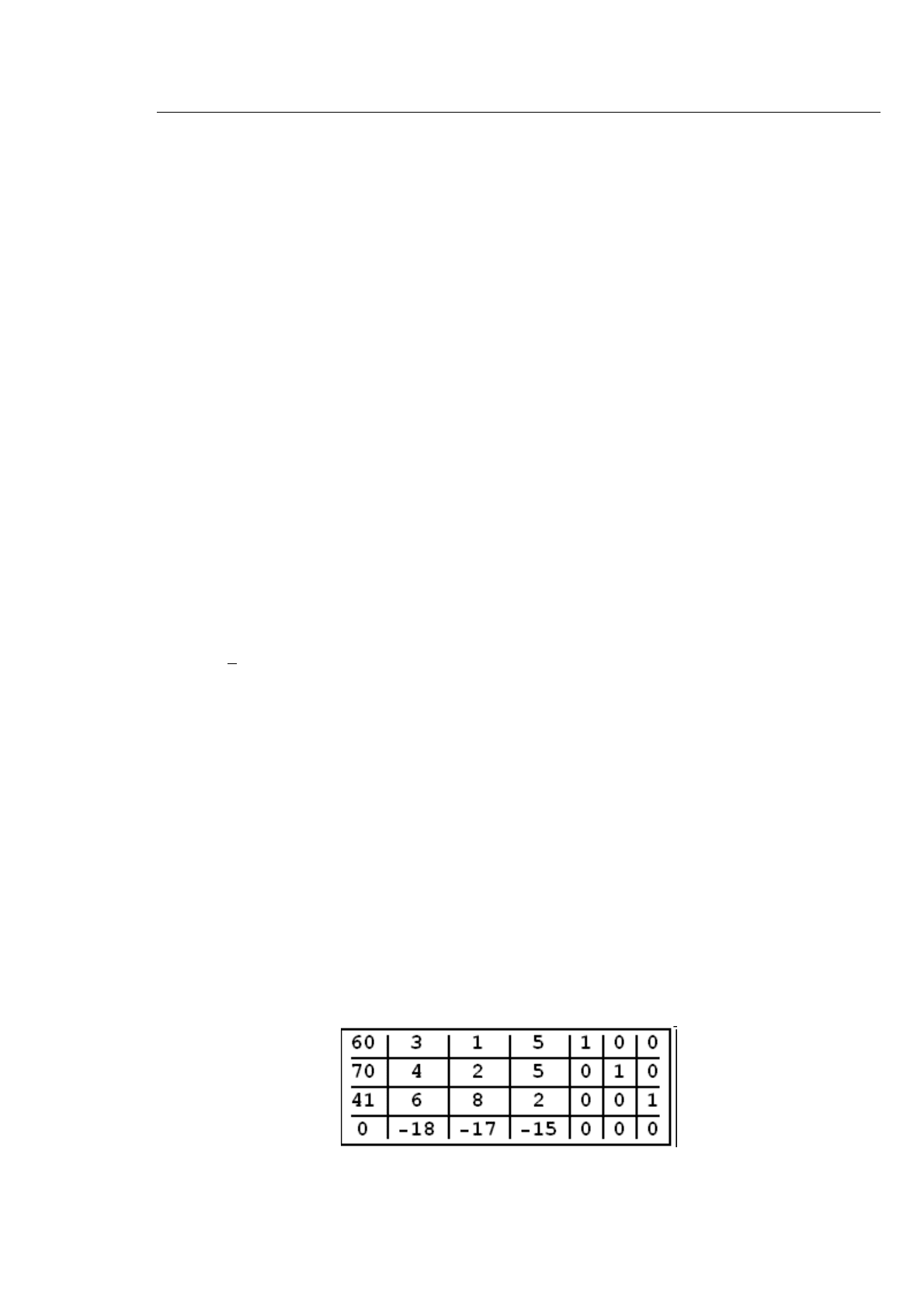
Сформируем первую таблицу симплекс-метода. Для этого к матрице

a добавим нулевые элемент

nl = Table[0, n];

к последней строке справа и единичную матрицу

nm = IdentityMatrix[n];

также справа, вектор (−c) в последнюю строку и столбец b слева. В

результате получим матрицу

d = Join[Table[{b[[i]], a[[i]], nm[[i]]}//Flatten, {i, 1, n}],

{Join[{0}, −c, nl]}];

Для просмотра результата в этом месте можно выполнить команду

hf[d] :

Введем счетчик итераций

86 ГЛАВА 2. ПРОГРАММИРОВАНИЕ В МАТЕМАТИКЕ

op = 1;

Создадим первую строку таблицы и первый столбец базисных пере-

менных

dg = Join[{”Баз.пер.”, ”Св.чл.”}, Table[”x” <> ToString[i],

{i, 1, 2n}], {θ}];

dl = Append[Table[”x” <> ToString[i], {i, n + 1, 2n}], L[

]];

Эти элементы таблицы будут присоеденены к матрицы a перед са-

мым выводом таблицы на экран.

Вводим пустой список res :

res = {};

Следующая команда является первой командой в команде While и

проверяет наличие отрицательных элементов в индексной строке та-

блицы

MemberQ[Table[d[[n + 1, i]] < 0, {i, 2, 2n + 1}], True]

Если эта команда возвращает значение ”True,” то присоединяем к

таблице a последний столбец с элементами ”-”. Далее, элементы это-

го столбца будут заменены отношениями соответствующих элементов

столбца свободных членов на положительные элементы направляюще-

го столбца:

d1 = Transpose[Append[Transpose[d], Table[” − ”, {i, 1, n + 1}]]])

Находим минимальный элемент индексной строки

m = Min[Table[d[[n + 1, i]], {i, 2, 2n + 1}]]

Определяем позицию минимального элемента в индексной строке и,

тем самым, определяем направляющий столбец

in = Position[d[[n + 1]], m][[1, 1]]

Создаем столбец θ отношений элементов свободных членов на поло-

жительные элементы направляющего столбца

t = Table[If[d[[i, in]] > 0, d[[i, 1]]/d[[i, in]], Inﬁnity], {i, 1, n}]

В столбце θ находим минимальный элемент

mt = Min[Table[t[[i]], {i, 1, n}]]

и находим его позицию в этом столбце (тем самым определена напра-

вляющая строка и разрешающий элемент, стоящий на пересечении на-

правляющих строки и столбца):

int = Position[t, mt][[1, 1]];

Следующие команды начинают преобразование таблицы по схеме

Гаусса. Делим элементы направляющей строки на разрешающий эле-

мент и полученную строку заносим в новую таблицу

d = d/.d[[int]]− > d[[int]]/d[[int, in]]

2.1 Примеры программирования в Математике 87

и преобразовываем остальные строки так, чтобы над единицей напра-

вляющей строки в новой таблице стояли нулевые элементы

Do[If[k 6= int, d[[k]] = d[[k]] − d[[int]]d[[k, in]]], {k, 1, n + 1}]

Вводим номер итерации в обозначении функции, тем самым заменя-

ем первый столбец на столбец

dll = dl/.u− > op

К столбцу θ добавим снизу одно тире:

d1[[All, 2n + 2]] = Append[t, ” − ”];

Выделим цветом минимальный элемент индексной строки, мини-

мальный элемент столбца θ (красным) и разрешающий элемент синим

цветом. Для этого запомним эти элементы:

pom = d1[[int, in]];

pX = d1[[n + 1, in]];

pY = d1[[int, 2n + 2]];

и изменим их цвет, размер и начертание

d1[[int, in]] = StyleForm[d1[[int, in]],

FontColor− > RGBColor[0, .1, 1], FontFamily− > ”Times”];

d1[[n + 1, in]] = StyleForm[d1[[n + 1, in]],

FontColor− > RGBColor[1, .1, .1], FontFamily− > ”Times”];

d1[[int, 2n + 2]] = StyleForm[d1[[int, 2n + 2]],

FontColor− > RGBColor[1, .1, .1], FontFamily− > ”Times”];

Полученную таблицу дополняем заголовком (первой строкой) и пер-

вым столбцом и вносим в массив вывода

res = Append[res,

Prepend[Transpose[Prepend[Transpose[d1], dll]], dg]];

Возвращаем первоначальный облик измененным элементам

d1[[int, in]] = pom;

d1[[n + 1, in]] = pX;

d1[[int, 2n + 2]] = pY;

Заменяем базисную переменную на переменную направляющего столб-

ца

dl[[int]] = dg[[in + 1]]

и увеличиваем номер итерации на единицу

op = op + 1;

На этой команде заканчивает набор команд, входящих в команда

While. Последняя команда перестает работать, если элементы индекс-

ной строки на некоторой итерации становятся неотрицательными. Сфор -

мированный список таблиц res требует вывода на экран. Добавляем к

88 ГЛАВА 2. ПРОГРАММИРОВАНИЕ В МАТЕМАТИКЕ

этому списку в качестве последнего элемента таблицу ответ с выре -

занным последним вспомогательным столбцом

res = Append[res,

Prepend[Transpose[Prepend[Transpose[d], dll]], Drop[dg, −1]]];

и выводим все таблицы на экран

Print[hf[#]]&/@res;

Следующие строки формирую ответ. Сначала выводим на экран

максимальное значение целевой функции, которое хранится в (n + 1, 1)

месте таблицы d, то есть является значением переменной d[[n + 1, 1]].

Print[”Ответ : максим .значениефункции”, ”L[

X”

, ”]”, ” = ”,

d[[n + 1, 1]], ”при”];

Для вывода на экран значений x-ов, дающих максимум целевой функ-

ции, необходимо выяснить, какие переменные входят в первый столбец

таблицы ответа. Команда MemberQ[dl, ”x” <> ToString[i]] проверя-

ет, входит ли элемент xi в первый столбец, и, если входит (значение

команды есть True), то определяется его позиция в этом столбце, кото-

рая позволяет найти значение найденной переменной во втором столбце

таблицы. Переменной, не входящей в первый столбец, присваивается

нулевое значение.

Do[Print[”x” <> ToString[i] <> ” = ”,

If[MemberQ[dl, ”x” <> ToString[i]],

p = Position[dl, ”x” <> ToString[i]][[1, 1]]; d[[p, 1]], 0]], {i, 1, n}]

Объединяя рассмотренные команды в единый блок, составим новую

команду, решающую поставленную задачу:

simplex[a1 , b1 , c1 ] := Block[{n}, a = a1; b = b1; c = c1;

n = Length[a];

nl = Table[0, {n}];

nm = IdentityMatrix[n];

d = Join[Table[Flatten[{b[[i]], a[[i]], nm[[i]]}, {i, 1, n}],

{Join[{0}, −c, nl]}];

op = 1;

dg = Join[{”Баз.пер.”, ”Св.чл.”},

Table[”x” <> ToString[i], {i, 1, 2n}], {θ}];

dl = Append[Table[”x” <> ToString[i], {i, n + 1, 2n}], L[

]];

dll = dl/.u− > op;

res = {};

While[MemberQ[Table[d[[n + 1, i]] < 0, {i, 2, 2n + 1}], True],

d1 = Transpose[Append[Transpose[d],

2.1 Примеры программирования в Математике 89

Table[” − ”, {i, 1, n + 1}]]];

m = Min[Table[d[[n + 1, i]], {i, 2, 2n + 1}]];

in = Position[d[[n + 1]], m][[1, 1]];

t = Table[If[d[[i, in]] > 0, d[[i, 1]]/d[[i, in]], Inﬁnity], {i, 1, n}];

mt = Min[[t[[i]], {i, 1, n}]];

int = Position[t, mt][[1, 1]];

d = d/.d[[int]]− > d[[int]]/d[[int, in]];

Do[If[k 6= int, d[[k]] = d[[k]] − d[[int]] d[[k, in]]], {k, 1, n + 1}];

dll = dl/.u− > op;

d1[[All, 2n + 2]] = Append[t, ” − ”];

pom = d1[[int, in]];

pX = d1[[n + 1, in]];

pY = d1[[int, 2n + 2]];

d1[[int, in]] = StyleForm[d1[[int, in]],

FontColor− > RGBColor[0, .1, 1], FontFamily− > ”Times”];

d1[[n + 1, in]] = StyleForm[d1[[n + 1, in]],

FontColor− > RGBColor[1, .1, .1], FontFamily− > ”Times”];

d1[[int, 2n + 2]] = StyleForm[d1[[int, 2n + 2]],

FontColor− > RGBColor[1, .1, .1], FontFamily− > ”Times”];

res = Append[res,

Prepend[Transpose[Prepend[Transpose[d1], dll]], dg]];

d1[[int, in]] = pom;

d1[[n + 1, in]] = pX;

d1[[int, 2n + 2]] = pY;

dl[[int]] = dg[[in + 1]];

op = op + 1; ];

dl[[int]] = dg[[in + 1]];

dll = dl/.u− > op;

res = Append[res,

Prepend[Transpose[Prepend[Transpose[d], dll]], Drop[dg, −1]]];

Print[hf[#]]&/@res;

Print[”Ответ : максим .значениефункции”,

”L[

X”

, ”]”, ” = ”, d[[n + 1, 1]], ”при”];

Do[Print[”x” <> ToString[i] <> ” = ”,

If[MemberQ[dl, ”x” <> ToString[i]],

p = Position[dl, ”x” <> ToString[i]][[1, 1]]; d[[p, 1]], 0]], {i, 1, n}]

]

Если команды hf[d] и simplex[a, b, c] введены, то ими можно поль-

90 ГЛАВА 2. ПРОГРАММИРОВАНИЕ В МАТЕМАТИКЕ

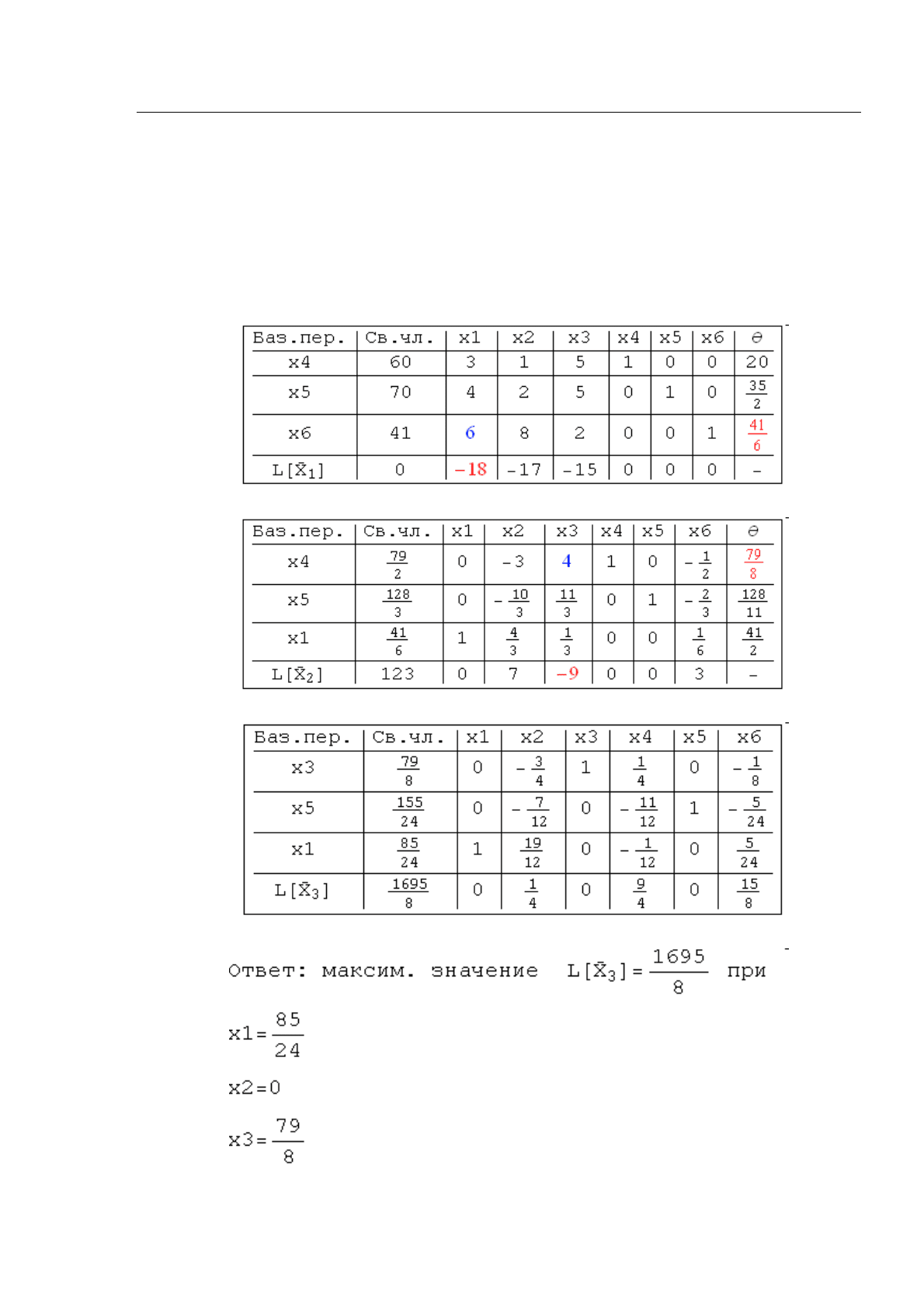
зоваться следующим образом. Допустим, что введены матрица a и

столбцы b и c Выполним теперь команду

simplex[a, b, c]

и получим результат ее действия: