Morris & Fan. Reservoir Sedimentation Handbook
Подождите немного. Документ загружается.

HYDRAULICS OF SEDIMENT TRANSPORT 9.14
action of the vegetation itself. Vegetative roughness can change both seasonally and over
the long term as vegetation grows.
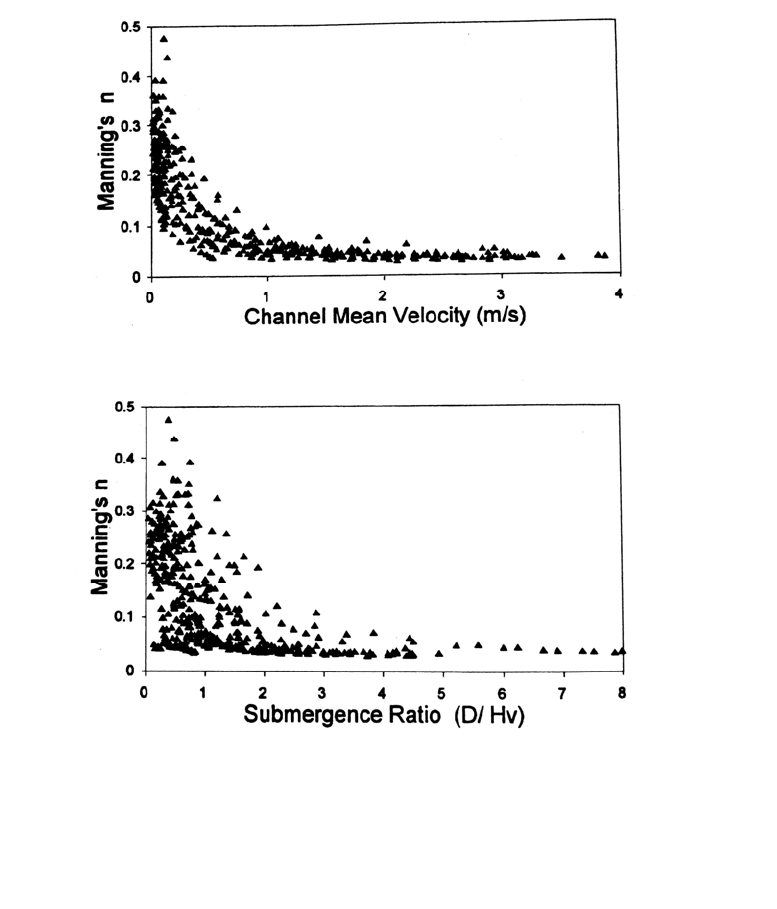
FIGURE 9.2 Variation in Manning's n value for grass channels (Torres, 1997).
The roughness value can change dramatically during flow events as vegetation is
inclined or flattened by the flow. Tones (1997) compiled data from 452 experiments in
grassed channels with flow depths from 0.018 to 0.81 m, and vegetation height ranging
from 0.05 to 0.9
,
m. As shown in Fig. 9.2, Manning's n value in vegetated channels is
initially high but subsequently drops to a range of about 0.03 to 0.07 for all types of
grasses analyzed when flow velocity exceeds about 1 m/s or the water depth D attains
about 3 times the vegetation height 1-4. The n value for areas with trees and shrubs which
are not flattened by flowing water can be affected seasonally by the presence or absence
of leaves, which create more drag than bare branches. In problems involving vegetation,
HYDRAULICS OF SEDIMENT TRANSPORT 9.15
the n value should be determined for the flow conditions and seasons of the year being
analyzed.
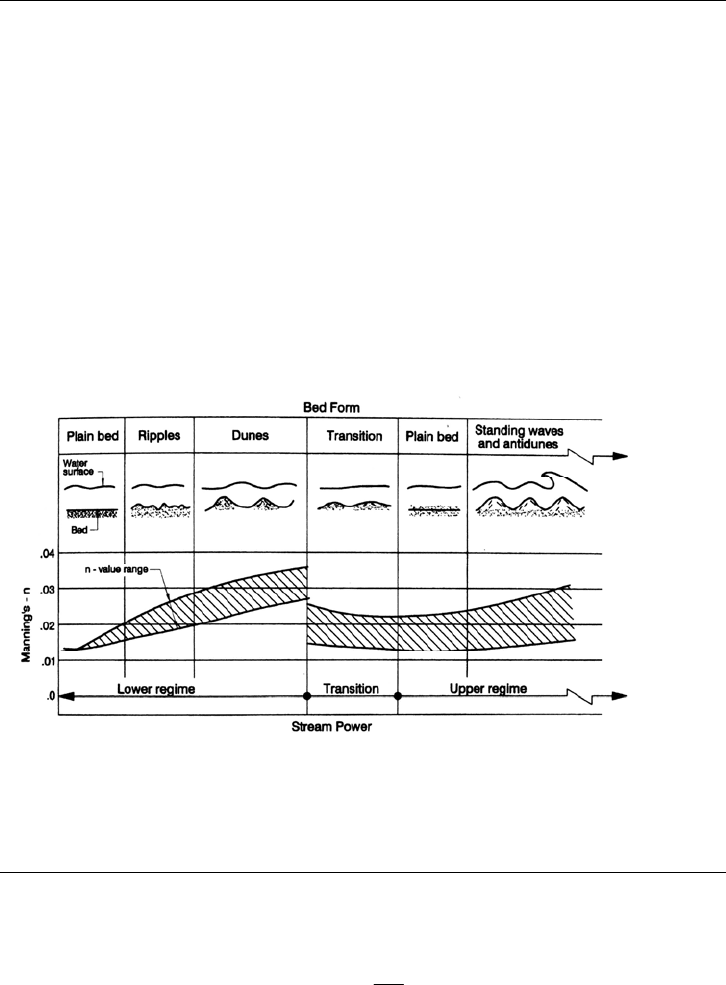
9.4 BED FORMS IN SAND-BED CHANNELS
Sand-bed channels are deformed by flow and the hydraulic roughness will vary greatly
depending on the bed configuration, as illustrated in Fig. 9.3. As flow velocity increases,
an initially flat sand bed develops first ripples and then dunes. With additional velocity,
the stream subsequently transitions into a plain bed form, and finally forms antidunes
with standing (stationary) waves which may or may not crest and break. Transition from
the lower flow regime, where bed forms dominate roughness, to the upper regime
produces a dramatic drop in roughness and will produce a discontinuous discharge rating
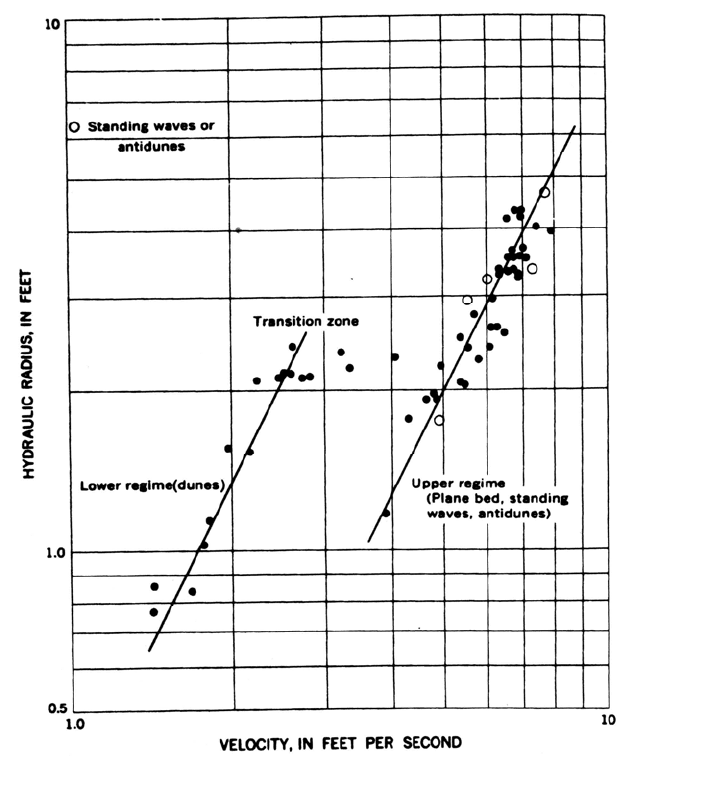
curve. For example, Nordin (1964) documented a threefold increase in flow velocity in
the Rio Grande near Bemalillo, New Mexico, with no increase in water level, because of
changing bed forms (Fig. 9.4). In gravel-bed rivers, bed forms tend to be poorly
developed and do not contribute significantly to flow resistance (Chang, 1988).
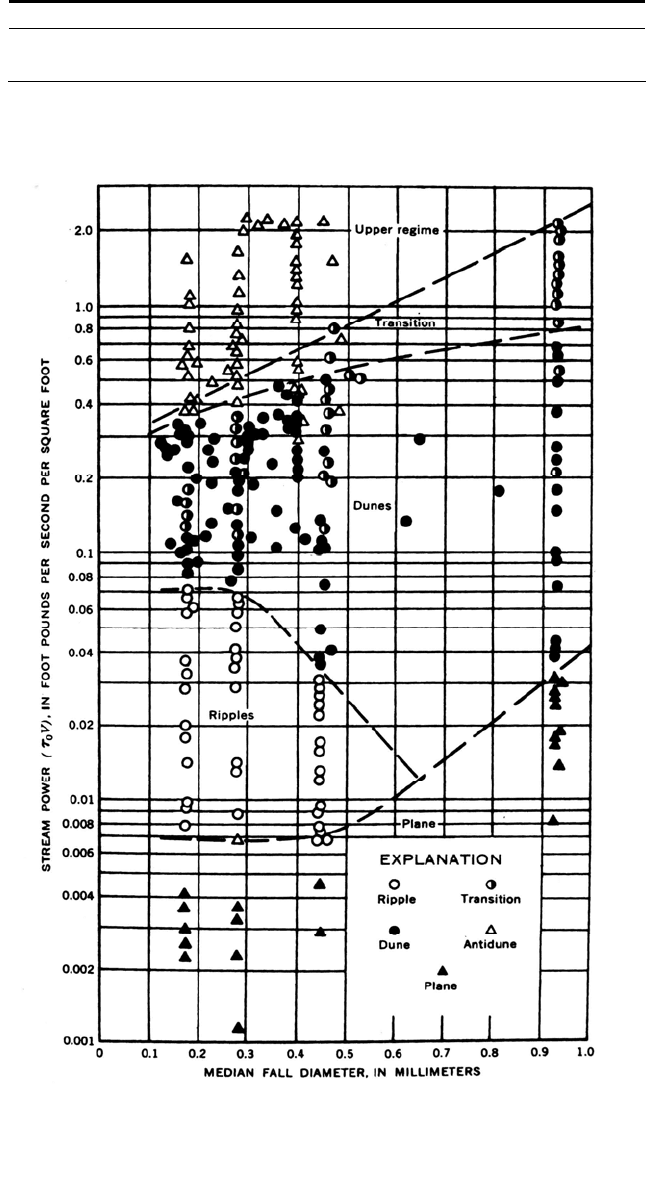
The relationship between bed form and stream power developed by Simons and
Richardson (1966) shown in Fig. 9.5 can be used to determine the flow regime. Because
of the nonuniform conditions in natural channels, different flow regimes and bed forms
can coexist in different areas of the same channel.
FIGURE 9.3 Bed forms encountered in movable bed streams.
9.5 VELOCITY DISTRIBUTION
9.5.1 Reynolds Number
The relation of viscous to inertial forces is expressed by the Reynolds number:
Re
VL
v
(9.8)
HYDRAULICS OF SEDIMENT TRANSPORT 9.16
FIGURE 9.4 Discontinuous rating curve on a sand-bed river (Nordin, 1964).
whe
re V = mean velocity, v = kinematic viscosity, and L = a characteristic length which
depends on the geometric properties of the cross section. Transmission of shear forces at
the boundary into the fluid creates a velocity profile in the fluid. When viscous forces
predominate, flow is said to be laminar and the fluid velocity varies linearly as the
function of distance from the boundary. When inertial forces predominate, the flow
regime is said to be turbulent and velocity varies logarithmically as a function of distance
from the boundary. Most civil engineering problems deal with turbulent flow.
The characteristic length is defined as a function of the cross-section geometry. The
characteristic lengths are L = flow depth for an open channel and L = roughness height or
grain diameter for the boundary Reynolds number. Therefore, the absolute values of the
Reynolds number which denote the transition from laminar to turbulent flow will depend
on the cross-section shape. A transition zone separates the laminar and fully developed
turbulent flow regimes. Reynolds number values relevant to open-channel and boundary
layer hydraulics are given in Table 9.6.
HYDRAULICS OF SEDIMENT TRANSPORT 9.17
TABLE 9.6 Reynolds Number
Flow regime Open channel Boundary
Laminar <500 <4
Turbulent >2000 >70
FIGURE 9.5 Prediction of bed form type based on stream power (Simons an
d
R
ichardson, 1966).
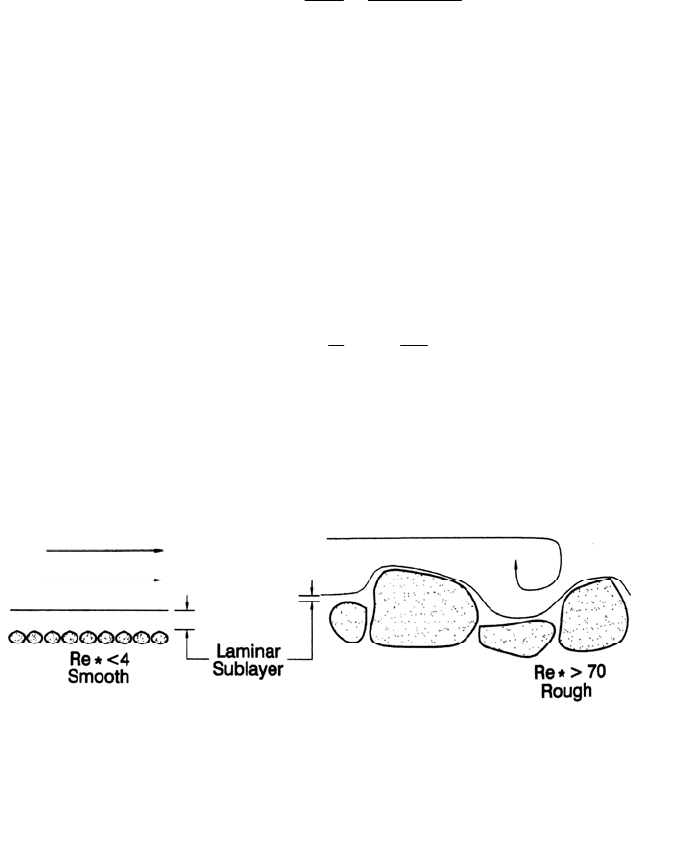
HYDRAULICS OF SEDIMENT TRANSPORT 9.18
9.5.2 Boundary Conditions
Fluid particles in immediate contact with a solid boundary have zero velocity. Even in
turbulent channels, a thin layer of laminar flow, termed the laminar sublayer, occurs next
to the solid boundary, where velocity is low and viscous forces predominate. When the
thickness of the laminar sublayer is greater than the height of the surface roughness
elements, the boundary is said to be hydraulically smooth. However, if the laminar
sublayer is thin and surface roughness elements protrude into the zone of turbulent flow,
thereby contributing to form drag, the boundary is said to be hydraulically rough. These
concepts are contrasted in Fig. 9.6. Most civil engineering problems deal with flows in
the fully turbulent range, where the laminar sublayer is very thin compared to the size of
the roughness elements. In this regime, the frictional resistance is independent of the
Reynolds number, but is a function of the roughness element size.
9.5.3 Boundary Reynolds Number
The shear velocity Reynolds number or boundary Reynolds number is defined as
Re
U
k
v
(gRS)
1/2
k
v
(9.9)
where U
*
= shear velocity, R = hydraulic radius, v = kinematic viscosity, S = slope, and k
= absolute roughness size. The k value is measured as the distance from the lowest to the
highest part of the protuberance into the fluid, but is also affected by the shape and
geometric configuration of roughness elements. The particle diameter d is commonly
substituted for k to compute Re
*
.
9.5.4 Vertical Velocity Distribution
For turbulent, nonstratified flow, the Prandtl-von Kármán universal velocity distribution
law expresses the local fluid velocity v
y
at a distance y from a boundary in the following
form:
0
ln
1
v
y
y
U
k
y
(9.10)
where the von Kármán constant κ = 0.4 and y
0
is a constant of integration. This
relationship may be used to determine the vertical distribution of flow velocity above the
bed of a wide prismatic channel.
When the boundary is hydraulically smooth, y
0
= m v
y
/U
*
, where m is a constant
having an experimentally determined value of about
1
/
9
. In this regime the roughness
FIGURE 9.6 At hydraulically smooth boundaries, the roughness elements remain
within the laminar sublayer. At a hydraulically rough boundary, the roughness
elements protrude through the laminar sub-layer.
HYDRAULICS OF SEDIMENT TRANSPORT 9.19
elements lie within the laminar sublayer, and therefore the velocity profile is influenced
by viscosity but is unaffected by the roughness characteristics. By substitution into Eq.
(9.10), the smooth-boundary velocity distribution for the hydraulically smooth regime is
v
yU
v
yU
U
y
ln5.25.5
9
ln5.2
v
(9.11)
For flow over a hydraulically rough boundary, y
0
= mk and the velocity distribution is
influenced by the absolute height of the roughness elements k, but is not influenced by
viscosity. In this case the constant m has a value of about
1
/
30
.
By substitution into Eq.
(9.10), the rough-boundary velocity distribution can be given by
k
y
k
y
U
y
ln5.25.8
30
ln5.2
v
(9.12)
To use Eqs. (9.11) and (9.12), compute shear velocity U
*
= (gRS)
1/2
, subsitituting R = D
as appropriate. In these equations y = height (m) above the bottom. In rivers and canals
the size of roughness elements can be estimated as k = 3d
90
, or k = 6d
50
if the d
90
value is
not known (Julien, 1995). When the velocity distribution is known from a minimum of
two points in a vertical, the k value may be computed. The effect of relative roughness
height relative to flow depth (k/D) on the shape of the velocity distribution for turbulent
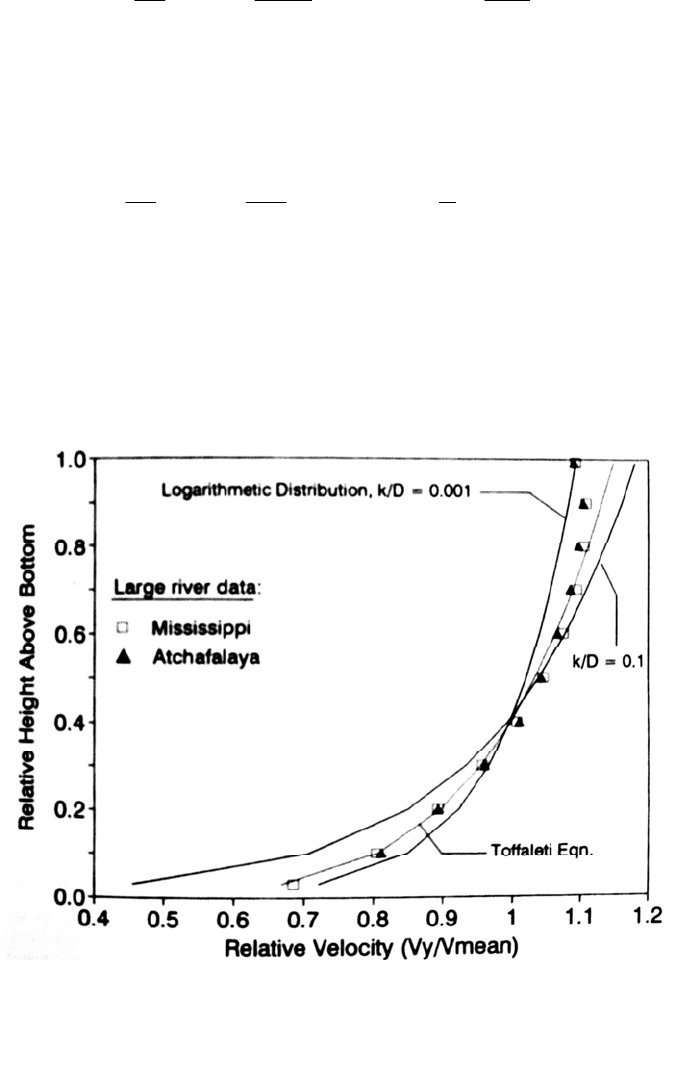
conditions is illustrated by the vertical velocity profiles in Fig. 9.7.
FIGURE 9.7 Vertical variation in velocity showing the logarithmic variation as
a function of relative roughness. The graph also presents data from the
Mississippi and Atchafalaya Rivers and the corresponding velocity distribution
suggested by Toffeleti (1963).

HYDRAULICS OF SEDIMENT TRANSPORT 9.20
By studying 973 measured vertical velocity profiles at two stations on the sand-bed
Mississippi and Atchafalaya Rivers, Toffaleti (1963) found that the vertical velocity
profiles in these two large rivers were essentially identical, but were somewhat different
from the profile derived from Eq. (9.12) (see Fig. 9.7). He fit the following velocity
profile equation to the data from these two large sand-bed rivers:
155.0
15.1v
D
y
V
y
(9.13)
where V = mean velocity at the cross section, y = height above the bottom, and D = total
depth. Flow curvature, channel irregularities, tributary inflows, and stratification will all
significantly influence the vertical velocity profile. The tangential component of flow can
be particularly important at curves and is discussed in more detail by Chang (1988).
9.5.5 Velocity Profile Measurement
According to the velocity relation produced by the logarithmic velocity distribution, the
mean velocity at a vertical can be estimated by point measurements at specific depths
below the water surface. Velocity measurements at the following points can be used to
estimate mean flow velocity at a vertical.
1. When one point is used, velocity at 60 percent of total depth will approximate mean
velocity.
2. If two points are used, measure at 20 and 80 percent of total depth and average the
two velocities.
3. If three points are used, measure at 20, 60, and 80 percent of total depth. First
average the 20 and 80 percent velocities, and then average the resultant velocity with
the velocity at 60 percent depth:
2
v
4
vv
608020
mean
V (9.14)
The measurement procedure is repeated at multiple verticals across the cross section to
obtain the mean velocity. Single-point measurements may be used in shallow water and
multiple points at deeper verticals.
9.5.6 Horizontal Velocity Distribution
The horizontal variation in both flow velocity and discharge across a stream will depend
on changes in the stream cross section and curvature. There is no general solution for the
horizontal variation in flow velocity in irregular natural channels.
9.6 VERTICAL DISTRIBUTION OF SEDIMENT
CONCENTRATION
Under conditions of steady uniform flow, the tendency for sediment to settle under the
influence of gravity is offset by the vertical component of turbulence in the water
column, a process known as turbulent diffusion. The upward-moving water comes from
the deeper zone with higher concentration, partially offsetting the settling of the sediment
and creating a vertical concentration gradient which can be described using the Rouse
equation:
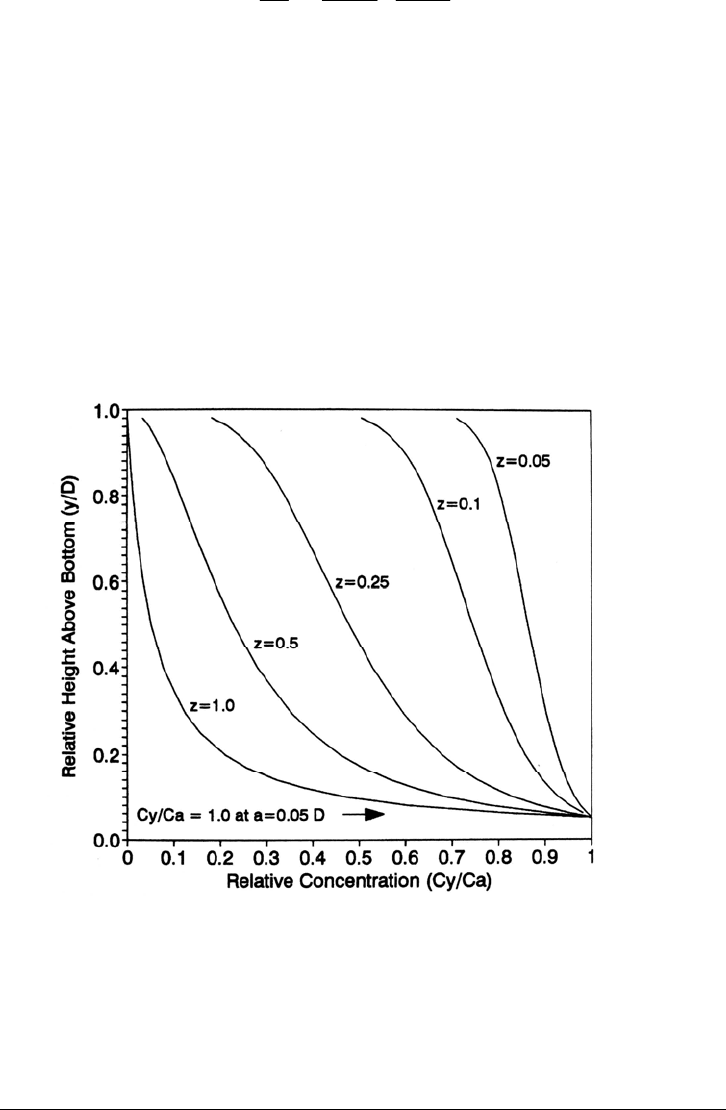
HYDRAULICS OF SEDIMENT TRANSPORT 9.21
C
y
C
a
D y
y
a
D a
z
(9.15)
where C
y
and C
a
= concentrations of sediment having fall velocity ω at vertical distances
y and a above the bed and D = total depth. In this equation z = (ω /κU
*
) where κ = 0.4 is
von Kármán's constant. This equation can be used to determine the concentration C
y
, at
any height y above the bottom relative to the known concentration C
a
at height a above
the bed. The value of z will decrease as fall velocity to decreases, producing a more
uniform vertical concentration distribution for finer sediment. Thus, a different vertical
distribution will exist for each size class. Concentration distributions for several values of
z are illustrated in Fig. 9.8, assigning a concentration C
a
= 1.0 at height a = 0.05D. The
equation should not be used at its extreme limits, since concentration calculates as zero at
the exact water surface and infinite at the bottom. The Rouse equation applies to
equilibrium conditions and may not be applicable to many situations in reservoirs where
rivers are depositing their sediment load and are thus not at equilibrium. The vertical
distribution of suspended sediment in reservoirs can also be influenced by stratification.
FIGURE 9.8 Vertical variation in suspended sediment concentration relative to the
concentration, C
a
= 1.0 at a/D = 0.05, for differ nt fall velocities. Concentrations are plottee
d
over the range of relative depths 0.98>y/D>0.05, and the variation in fall velocity is
expressed by the parameter z.
9.7 INITIATION OF MOTION
The motion of a fluid flowing across its bed tends to move the bed material downstream.
Below some critical condition, the hydraulic forces will be so small that particles will be
HYDRAULICS OF SEDIMENT TRANSPORT 9.22
moved very rarely or not at all. However, a slight increase in velocity above this critical
condition will initiate appreciable motion by some of the particles on the bed. This
critical condition is termed the condition of initiation of motion, and is commonly
computed in terms of either the critical mean flow velocity in the vertical or the critical
bed shear stress (also known as tractive force). As pointed out by Lavelle and Mofjeld
(1987), there is not truly a precise threshold value for the onset of sediment motion.
Rather, sediment transport rate declines continuously as flow velocity declines. The so-
called "critical value" actually refers to a very small rate of transport, and has been
defined differently by various researchers.
In a cohesionless bed, sediment movement is first initiated by an individual particle
which rolls or jumps a short distance before coming to rest. This movement is followed
by similar movement of a different particle. As the flow velocity increases, the number of
particles in motion and the distance traveled before coming to rest increases, until at
some higher velocity the entire bed is completely mobilized. In 1936 Shields defined the
critical condition of incipient motion as the point of zero transport, as extrapolated from
conditions under which measurable transport occurred. Others have defined this point
using terms such as weak movement, and the condition of incipient motion is somewhat
subjective. In a bed containing a range of sediment sizes, at intermediate flow velocities
only the smaller particles in the bed will be transported while the larger particles remain
stable.
Engineering interest in determining the critical flow velocity which initiates the scour
of sediment particles originated in the design of stable (nonscouring and nonsedimenting)
earthen canals. Much of the early work in this field was derived from experience gained
in the construction of irrigation canals in colonial India and Pakistan. There are two basic
approaches to the determination of the critical condition in open channels: the bed shear
(tractive force) approach, and the velocity approach. Both approaches have a long history
of use and an extensive literature. Although the initiation of motion of bed material is
determined by the flow velocity at the water-sediment boundary, velocity at the bed is
rarely measured and there is no agreement as to the distance above the bed that should be
considered as "bottom velocity." Therefore, as a practical matter, the critical velocity is
normally computed from the mean velocity across a vertical or the cross-sectional area.
9.7.1 Bed Shear or Tractive Force
For steady uniform flow, the specific weight of a column of water can be divided into
two vectors, one oriented perpendicular to the bed and one oriented along the bed in the
direction of flow. Under conditions of steady uniform flow, the component of the
gravitational force exerted along the slope direction which causes downstream motion is
balanced by the bed shear stress or tractive force τ
0
, which is the frictional force exerted
on the moving fluid at its boundary. Bed shear stress is not the force on individual
particles, but the force exerted over an area of the channel bed or banks. For the small
slopes normally encountered in hydraulic problems, the bed shear stress in a wide
channel can be computed as:
0
DS (9.16)
For the more general case, the depth term is replaced with the hydraulic radius to give:
0
R
S (9.17)
This concept of tractive force was first introduced by duBoys in 1879 in studies of the
movable bed of the Rhone River.
HYDRAULICS OF SEDIMENT TRANSPORT 9.23
9.7.2 Approximate Methods
The simplest method for estimating the threshold or critical condition for the movement
of cohesionless sediment is using the linear relationship between critical bed shear stress
(
cr
)
and grain size given by Julien (1995), reproduced below in several different systems
of units:
cr
(N/m
2
) = 0.785d
50
(mm) (9.18)
cr
(g/m
2
)
= 80d
50
(mm) (9.19)
cr
(lb/ft
2
) = 0.0164d
50
(mm) (9.20)
cr
(lb/ft
2
) = 5d
50
(ft) (9.21)
These equations are approximately valid for d
50
>0.3 mm (d
50
>0.001 ft) and can be used
as a quick check against other methods and to help determine the hydraulic roughness
regime. A similar linear relationship was suggested in 1955 by Leliavsky (cited by Graf,
1971). Figure 9.11 may also be consulted.
9.7.3 Empirical Criteria
The "permissible" velocities in canals do not necessarily correspond to a condition of
zero sediment transport, but rather to an equilibrium condition which does not produce
objectionable rates of either scour or deposition, even though the canal may be
transporting sediment along its bed. A well-known compilation of empirical data based
on experience with stable canals was prepared by Lane (1955) for the U.S. Bureau of
Reclamation and is a useful practical guide (Fig. 9.9). In using this figure recall the bed
shear conversion, 1 N/m
2
= 0.00981 g/m
2
. Curved canal sections tolerate lower velocity
and tractive force than straight canal sections.
Lane noted that canal engineers had long observed that nonscouring velocities are
higher in large canals than in small ones. Small shallow canals erode at a lower mean
velocity than large ones. He argued in favor of the tractive force approach rather than the
limiting velocity approach as the basis for canal design because it produced predictions
more consistent with these field observations. This effect is demonstrated in the example
computations in Secs. 9.7.7 and 9.7.8.
9.7.4 Shields Diagram
The Shields diagram (Fig. 9.10) is a widely used method to determine the condition of
incipient motion based on bed shear stress. Points lying above the curve representing the
critical condition correspond to sediment motion, and points below the curve correspond
to no motion. Shields determined that the critical condition could be related to two
dimensionless parameters: the dimensionless shear stress F. (also known as the Shields
parameter), which does not represent the actual shear stress, and the boundary Reynolds
number Re
= U
d/v.
The Shields parameter reflects the ratio of the force producing sediment motion to the
force resisting motion. The force producing motion is expressed by the product of the bed
shear stress τ
0
and the cross-sectional area of the particle exposed to the flow, represented
by the square of the particle diameter d
2
. The force resisting motion is the product of the
submerged unit weight of the sediment
(
s
-)
and particle volume, represented by the
