Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics

Подождите немного. Документ загружается.

so that the gas undergoes a throttling process (Sec. 4.10) as it expands from 1 to 2. Accord-

ingly, the exit state fixed by p

and T

has the same value for the specific enthalpy as

at the inlet, h

5 h

. By progressively lowering the outlet pressure, a finite sequence

of such exit states can be visited, as indicated on Fig. 11.3b. A curve may be drawn

through the set of data points. Such a curve is called an isenthalpic (constant enthalpy)

curve. An isenthalpic curve is the locus of all points representing equilibrium states

of the same specific enthalpy.

The slope of an isenthalpic curve at any state is the Joule–Thomson coefficient at

that state. The slope may be positive, negative, or zero in value. States where the coef-

ficient has a zero value are called inversion states. Notice that not all lines of constant

h have an inversion state. The uppermost curve of Fig. 11.3b, for example, always has

a negative slope. Throttling a gas from an initial state on this curve would result in an

increase in temperature. However, for isenthalpic curves having an inversion state, the

temperature at the exit of the apparatus may be greater than, equal to, or less than the

initial temperature, depending on the exit pressure specified. For states to the right of

an inversion state, the value of the Joule–Thomson coefficient is negative. For these

states, the temperature increases as the pressure at the exit of the apparatus decreases.

At states to the left of an inversion state, the value of the Joule–Thomson coefficient

is positive. For these states, the temperature decreases as the pressure at the exit of the

device decreases. This can be used to advantage in systems designed to liquefy gases.

An innovation in power systems moving from con-

cept to reality promises to help keep computer networks

humming, hospital operating rooms lit, and shopping cen-

ters thriving. Called distributed generation systems, compact

power plants provide electricity for small loads or are linked for

larger applications. With distributed generation, consumers hope

to avoid unpredictable price swings and brownouts.

Distributed generation includes a broad range of technologies

that provide relatively small levels of power at sites close to users,

including but not limited to internal combustion engines, micro-

turbines, fuel cells, and photovoltaic systems.

Although the cost per kilowatt-hour may be higher with dis-

tributed generation, some customers are willing to pay more

to gain control over their electric supply. Computer networks

and hospitals need high reliability, since even short disrup-

tions can be disastrous. Businesses such as shopping centers

also must avoid costly service interruptions. With distributed

generation, the needed reliability is provided by modular units

that can be combined with power management and energy

storage systems to ensure quality power is available when

needed.

Small Power Plants Pack Punch

inversion states

11.6 Constructing Tables of

Thermodynamic Properties

The objective of this section is to utilize the thermodynamic relations introduced thus

far to describe how tables of thermodynamic properties can be constructed. The

characteristics of the tables under consideration are embodied in the tables for water

and the refrigerants presented in the Appendix. The methods introduced in this sec-

tion are extended in Chap. 13 for the analysis of reactive systems, such as gas turbine

and vapor power systems involving combustion. The methods of this section also

provide the basis for computer retrieval of thermodynamic property data.

Two different approaches for constructing property tables are considered:

c The presentation of Sec. 11.6.1 employs the methods introduced in Sec. 11.4 for

assigning specific enthalpy, specific internal energy, and specific entropy to states of

pure, simple compressible substances using p–y–T data, together with a limited

amount of specific heat data. The principal mathematical operation of this approach

is integration.

11.6 Constructing Tables of Thermodynamic Properties 663

c11ThermodynamicRelations.indd Page 663 6/21/10 9:34:50 PM user-s146c11ThermodynamicRelations.indd Page 663 6/21/10 9:34:50 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

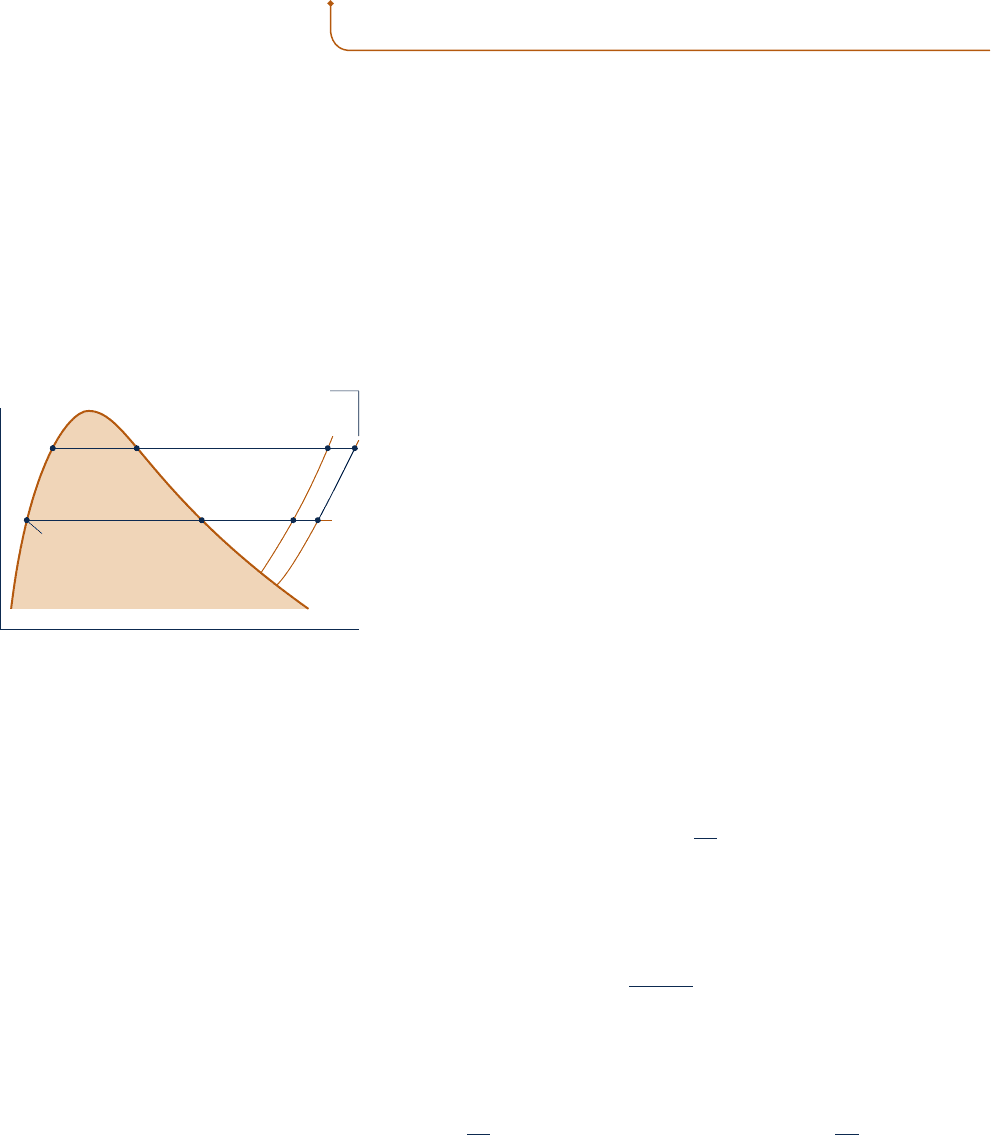
664 Chapter 11

Thermodynamic Relations

c The approach of Sec. 11.6.2 utilizes the fundamental thermodynamic function con-

cept introduced in Sec. 11.3.3. Once such a function has been constructed, the

principal mathematical operation required to determine all other properties is

differentiation.

11.6.1

Developing Tables by Integration Using p–y–T and

Specific Heat Data

In principle, all properties of present interest can be determined using

5 c

1T2 (11.78)

p 5 p1y, T2, y 5 y1p, T2

In Eqs. 11.78, c

(T) is the specific heat c

for the substance under consideration

extrapolated to zero pressure. This function might be determined from data obtained

calorimetrically or from spectroscopic data, using equations supplied by statistical mechan-

ics. Specific heat expressions for several gases are given in Tables A-21. The expressions

p(y, T) and y(p, T) represent functions that describe the saturation pressure–temperature

curves, as well as the p–y–T relations for the single-phase regions.

These functions may be tabular, graphical, or analytical in character.

Whatever their forms, however, the functions must not only represent

the p–y–T data accurately but also yield accurate values for deriva-

tives such as 10y

0T2

and 1dp

dT2

sat

Figure 11.4 shows eight states of a substance. Let us consider how

values can be assigned to specific enthalpy and specific entropy at

these states. The same procedures can be used to assign property

values at other states of interest. Note that when h has been assigned

to a state, the specific internal energy at that state can be found from

u 5 h 2 py.

c Let the state denoted by 1 on Fig. 11.4 be selected as the datum

state for enthalpy and entropy. Any value can be assigned to h and

s at this state, but a value of zero would be usual. It should be

noted that the use of an arbitrary datum state and arbitrary refer-

ence values for specific enthalpy and specific entropy suffices only

for evaluations involving differences in property values between

states of the same composition, for then datums cancel.

c Once a value is assigned to enthalpy at state 1, the enthalpy at the saturated vapor

state, state 2, can be determined using the Clapeyron equation, Eq. 11.40

2 h

5 T

2 y

sat

where the derivative (dp/dT)

sat

and the specific volumes y

and y

are obtained

from appropriate representations of the p–y–T data for the substance under con-

sideration. The specific entropy at state 2 is found using Eq. 11.38 in the form

2 s

2 h

c Proceeding at constant temperature from state 2 to state 3, the entropy and enthalpy

are found by means of Eqs. 11.59 and 11.60, respectively. Since temperature is fixed,

these equations reduce to give

2 s

and

2 h

cy 2 T a

d dp

With the same procedure, s

and h

can be determined.

Arbitrary datum

state h

= s

= 0

234

765

Isobar–

reduced pressure

low enough

for the ideal gas

model to be

appropriate

Fig. 11.4 T–y diagram used to discuss how h

and s can be assigned to liquid and vapor

states.

c11ThermodynamicRelations.indd Page 664 6/21/10 9:34:50 PM user-s146c11ThermodynamicRelations.indd Page 664 6/21/10 9:34:50 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

c The isobar (constant-pressure line) passing through state 4 is assumed to be at a

low enough pressure for the ideal gas model to be appropriate. Accordingly, to

evaluate s and h at states such as 5 on this isobar, the only required information

would be c

(T) and the temperatures at these states. Thus, since pressure is fixed,

Eqs. 11.59 and 11.60 give, respectively

2 s



and



2 h

c Specific entropy and enthalpy values at states 6 and 7 are found from those at state

5 by the same procedure used in assigning values at states 3 and 4 from those at

state 2. Finally, s

and h

are obtained from the values at state 7 using the Clapeyron

equation.

11.6.2

Developing Tables by Differentiating a Fundamental

Thermodynamic Function

Property tables also can be developed using a fundamental thermodynamic function.

It is convenient for this purpose to select the independent variables of the fundamen-

tal function from among pressure, specific volume (density), and temperature. This

indicates the use of the Helmholtz function c(T, y) or the Gibbs function g(T, p). The

properties of water tabulated in Tables A-2 through A-6 have been calculated using the

Helmholtz function. Fundamental thermodynamic functions also have been employed

successfully to evaluate the properties of other substances in the Appendix tables.

The development of a fundamental thermodynamic function requires considerable

mathematical manipulation and numerical evaluation. Prior to the advent of high-

speed computers, the evaluation of properties by this means was not feasible, and the

approach described in Sec. 11.6.1 was used exclusively. The fundamental function

approach involves three steps:

The first step is the selection of a functional form in terms of the appropriate pair

of independent properties and a set of adjustable coefficients, which may number

50 or more. The functional form is specified on the basis of both theoretical and

practical considerations.

Next, the coefficients in the fundamental function are determined by requiring

that a set of carefully selected property values and/or observed conditions be

satisfied in a least-squares sense. This generally involves the use of property data

requiring the assumed functional form to be differentiated one or more times, such

as p–y–T and specific heat data.

When all coefficients have been evaluated, the function is carefully tested for

accuracy by using it to evaluate properties for which accepted values are known.

These may include properties requiring differentiation of the fundamental function

two or more times. For example, velocity of sound and Joule–Thomson data might

be used.

This procedure for developing a fundamental thermodynamic function is not routine

and can be accomplished only with a computer. However, once a suitable fundamen-

tal function is established, extreme accuracy in and consistency among the thermo-

dynamic properties is possible.

The form of the Helmholtz function used in constructing the steam tables from

which Tables A-2 through A-6 have been extracted is

c1r, T25 c

1T21 RT 3ln r 1 rQ1r,t24 (11.79)

where c

and Q are given as the sums listed in Table 11.3. The independent variables

are density and temperature. The variable t denotes 1000/T. Values for pressure, specific

11.6 Constructing Tables of Thermodynamic Properties 665

c11ThermodynamicRelations.indd Page 665 6/21/10 9:34:53 PM user-s146c11ThermodynamicRelations.indd Page 665 6/21/10 9:34:53 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

666 Chapter 11 Thermodynamic Relations

internal energy, and specific entropy can be determined by differentiation of Eq. 11.79.

Values for the specific enthalpy and Gibbs function are found from h 5 u 1 py and

g 5 c 1 py, respectively. The specific heat c

is evaluated by further differentiation,

5 10u

0T2

. With similar operations, other properties can be evaluated. Property

values for water calculated from Eq. 11.79 are in excellent agreement with experimental

data over a wide range of conditions.

Fundamental Equation Used to Construct the Steam Tables

a,b

c 5 c

1T21 RT 3In r 1 rQ1r, t24 (1)

where

i5 1

i21

1 C

In T 1 C

In T

(2)

and

Q 5 1t 2 t

j5 1

1t 2 t

j2 2

i5 1

1r 2 r

i2 1

1 e

2 Er

i5 9

i2 9

(3)

In (1), (2), and (3), T denotes temperature on the Kelvin scale, t denotes 1000/T, r denotes density

in g/cm

, R 5 4.6151 bar ? cm

/g ? K or 0.46151 J/g ? K, t

5 1000/T

5 1.544912, E 5 4.8, and

5 t

1j 5 12 r

5 0.6341j 5 12

5 2.51j . 12 5 1.01j . 12

The coefficients for c

in J/g are given as follows:

5 1857.065 C

5 36.6649 C

5 46.0

5 3229.12 C

5 220.5516 C

5 21011.249

5 2419.465 C

5 4.85233

Values for the coefficients A

are listed in the original source.

TABLE 11.3

J. H. Keenan, F. G. Keyes, P. G. Hill, and J. G. Moore, Steam Tables, Wiley, New York, 1969.

Also see L. Haar, J. S. Gallagher, and G. S. Kell, NBS/NRC Steam Tables, Hemisphere, Washington, D.C., 1984.

The properties of water are determined in this reference using a different functional form for the Helmholtz

function than given by Eqs. (1)–(3).

ENERGY & ENVIRONMENT Due to the phase-out of chlorine-containing

CFC refrigerants because of ozone layer and global climate change concerns, new

substances and mixtures with no chlorine have been developed in recent years as

possible alternatives (see Sec. 10.3). This has led to significant research efforts to provide the

necessary thermodynamic property data for analysis and design.

The National Institute of Standards and Technology (NIST) has led governmental efforts

to provide accurate data. Specifically, data have been developed for high-accuracy p–y–T

equations of state from which fundamental thermodynamic functions can be obtained. The

equations are carefully validated using data for velocity of sound, Joule–Thomson coeffi-

cient, saturation pressure-temperature relations, and specific heats. Such data were used

to calculate the property values in Tables A-7 to A-18 in the Appendix. NIST has developed

REFPROP, a computer data base that is the current standard for refrigerant and refrigerant

mixture properties.

Example 11.7 illustrates the use of a fundamental function to determine thermo-

dynamic properties for computer evaluation and to develop tables.

c11ThermodynamicRelations.indd Page 666 7/25/10 5:16:49 PM user-f391c11ThermodynamicRelations.indd Page 666 7/25/10 5:16:49 PM user-f391 /Users/user-f391/Desktop/Ramakant_25.07.10/Moran_JWCL314/New/Users/user-f391/Desktop/Ramakant_25.07.10/Moran_JWCL314/New

Determining Properties Using a Fundamental Function

c c c c EXAMPLE 11.7 c

The following expression for the Helmholtz function has been used to determine the properties of water:

c1r, T25 c

1T21 RT 3ln r 1 rQ1r, t24

where r denotes density and t denotes 1000/T. The functions c

and Q are sums involving the indicated inde-

pendent variables and a number of adjustable constants (see Table 11.3). Obtain expressions for (a) pressure,

(b) specific entropy, and (c) specific internal energy resulting from this fundamental thermodynamic function.

SOLUTION

Known:

An expression for the Helmholtz function c is given.

Find: Determine the expressions for pressure, specific entropy, and specific internal energy that result from this

fundamental thermodynamic function.

Analysis: The expressions developed below for p, s, and u require only the functions c

(T) an Q(r, t). Once these

functions are determined, p, s, and u can each be determined as a function of density and temperature using

elementary mathematical operations.

(a) When expressed in terms of density instead of specific volume, Eq. 11.28 becomes

p 5 r

as can easily be verified. When T is held constant t is also constant. Accordingly, the following is obtained on

differentiation of the given function:

5 RT c

1 Q1r, t21 ra

Combining these equations gives an expression for pressure

p 5 rRT c1 1 rQ 1 r

(a)

(b) From Eq. 11.29

s 52a

Differentiation of the given expression for c yields

1 cR1ln r 1 rQ21 RTr a

1000

1 R cln r 1 rQ 2 rta

Combining results gives

s 52

2 R cln r 1 rQ 2 rta

(b)

expression for s from part (b) results in

u 5 3c

1 RT1ln r 1 rQ241 T e2

2 R cln r 1 rQ 2 rta

5 c

2 T

1 RTrt a

11.6 Constructing Tables of Thermodynamic Properties 667

c11ThermodynamicRelations.indd Page 667 6/21/10 9:35:52 PM user-s146 c11ThermodynamicRelations.indd Page 667 6/21/10 9:35:52 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

668 Chapter 11

Thermodynamic Relations

This can be written more compactly by noting that

5 T

1000

b52t

Thus,

2 T

5 c

1 t

d1c

Finally, the expression for u becomes

u 5

d1c

1 RTrt a

(c)

Using results obtained, how can an expression be developed

for h? Ans. h 5 u 1 p/r. Substitute Eq. (c) for u and Eq. (a) for p and

collect terms.

TAKE NOTE...

Generalized compressibility

charts are provided in

Appendix figures A-1, A-2,

and A-3. See Example 3.7

for an application.

Ability to…

❑

derive expressions for pres-

sure, specific entropy, and

specific internal energy

based on a fundamental

thermodynamic function.

✓

Skills Developed

11.7 Generalized Charts for Enthalpy

and Entropy

Generalized charts giving the compressibility factor Z in terms of the reduced

properties p

, T

, and y9

are introduced in Sec. 3.11. With such charts, estimates

of p–y–T data can be obtained rapidly knowing only the critical pressure and

critical temperature for the substance of interest. The objective of the present sec-

tion is to introduce generalized charts that allow changes in enthalpy and entropy

to be estimated.

Generalized Enthalpy Departure Chart

The change in specific enthalpy of a gas (or liquid) between two states fixed by tem-

perature and pressure can be evaluated using the identity

h1T

, p

22 h1T

, p

25 3h

22 h

1 53h1T

, p

22 h

242 3h1T

, p

22 h

246 (11.80)

The term [h(T, p) 2 h

(T)] denotes the specific enthalpy of the substance relative to

that of its ideal gas model when both are at the same temperature. The superscript

* is used in this section to identify ideal gas property values. Thus, Eq. 11.80 indicates

that the change in specific enthalpy between the two states equals the enthalpy

change determined using the ideal gas model plus a correction that accounts for the

departure from ideal gas behavior. The correction is shown underlined in Eq. 11.80.

The ideal gas term can be evaluated using methods introduced in Chap. 3. Next, we

show how the correction term is evaluated in terms of the enthalpy departure.

DEVELOPING THE ENTHALPY DEPARTURE. The variation of enthalpy with

pressure at fixed temperature is given by Eq. 11.56 as

5 y 2 T a

Integrating from pressure p9 to pressure p at fixed temperature T

h1T, p22 h1T, p¿25

p¿

cy 2 T a

d dp

c11ThermodynamicRelations.indd Page 668 6/21/10 9:35:54 PM user-s146 c11ThermodynamicRelations.indd Page 668 6/21/10 9:35:54 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

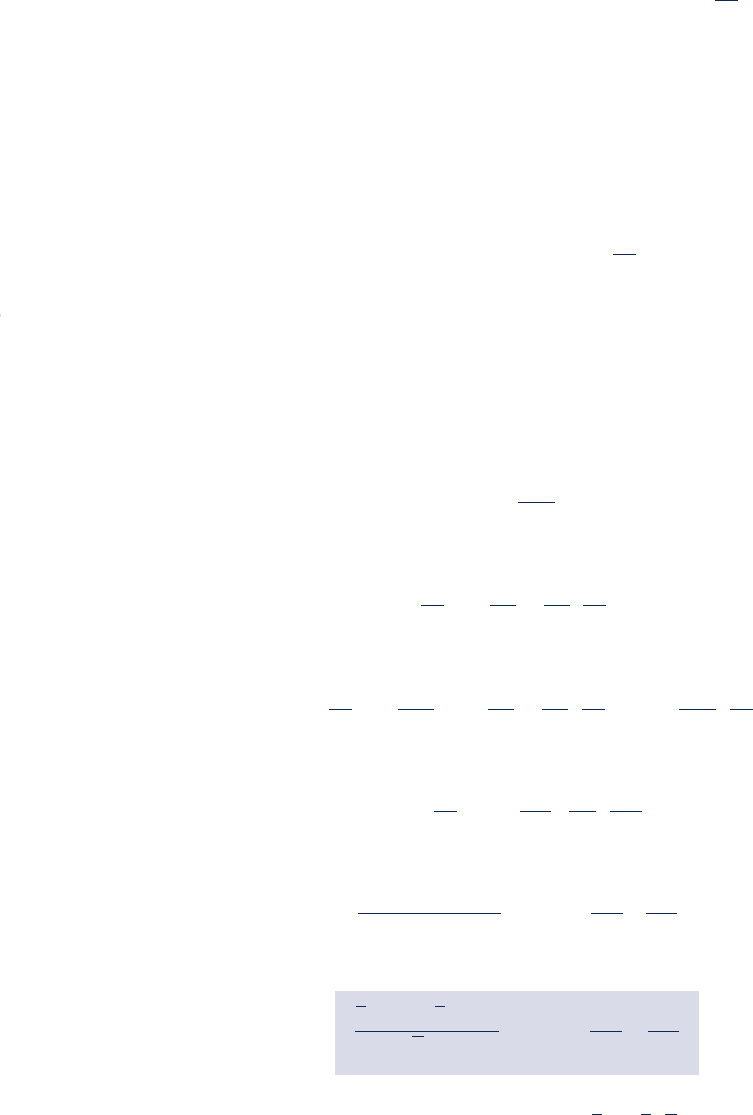
This equation is not altered fundamentally by adding and subtracting h*(T) on the

left side. That is

3h1T, p22 h

1T242 3h1T, p¿22 h

1T245

p¿

cy 2 T a

d dp

(11.81)

As pressure tends to zero at fixed temperature, the enthalpy of the substance

approaches that of its ideal gas model. Accordingly, as p9 tends to zero

lim

p¿S0

3h1T, p¿22 h

1T245 0

In this limit, the following expression is obtained from Eq. 11.81 for the specific

enthalpy of a substance relative to that of its ideal gas model when both are at the

same temperature:

h1T, p22 h

1T25

cy 2 T a

d dp

(11.82)

This also can be thought of as the change in enthalpy as the pressure is increased from

zero to the given pressure while temperature is held constant. Using p–y–T data only,

Eq. 11.82 can be evaluated at states 1 and 2 and thus the correction term of Eq. 11.80

evaluated. Let us consider next how this procedure can be conducted in terms of

compressibility factor data and the reduced properties T

and p

The integral of Eq. 11.82 can be expressed in terms of the compressibility factor

Z and the reduced properties T

and p

as follows. Solving Z 5 py/RT gives

y 5

ZRT

On differentiation

With the previous two expressions, the integrand of Eq. 11.82 becomes

y 2 T a

ZRT

2 T c

d52

(11.83)

Equation 11.83 can be written in terms of reduced properties as

y 2 T a

Introducing this into Eq. 11.82 gives on rearrangement

1T22 h1T, p

5 T

Or, on a per mole basis, the enthalpy departure is

1T22 h1T, p2

5 T

(11.84)

The right side of Eq. 11.84 depends only on the reduced temperature T

and

reduced pressure p

. Accordingly, the quantity 1h

2 h2

, the enthalpy depar-

ture, is a function only of these two reduced properties. Using a generalized equa-

tion of state giving Z as a function of T

and p

, the enthalpy departure can

readily be evaluated with a computer. Tabular representations are also found in

the literature. Alternatively, the graphical representation provided in Fig. A-4 can

be employed.

enthalpy departure

11.7 Generalized Charts for Enthalpy and Entropy 669

c11ThermodynamicRelations.indd Page 669 6/21/10 9:35:57 PM user-s146 c11ThermodynamicRelations.indd Page 669 6/21/10 9:35:57 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

670 Chapter 11

Thermodynamic Relations

Using the Generalized Enthalpy Departure Chart

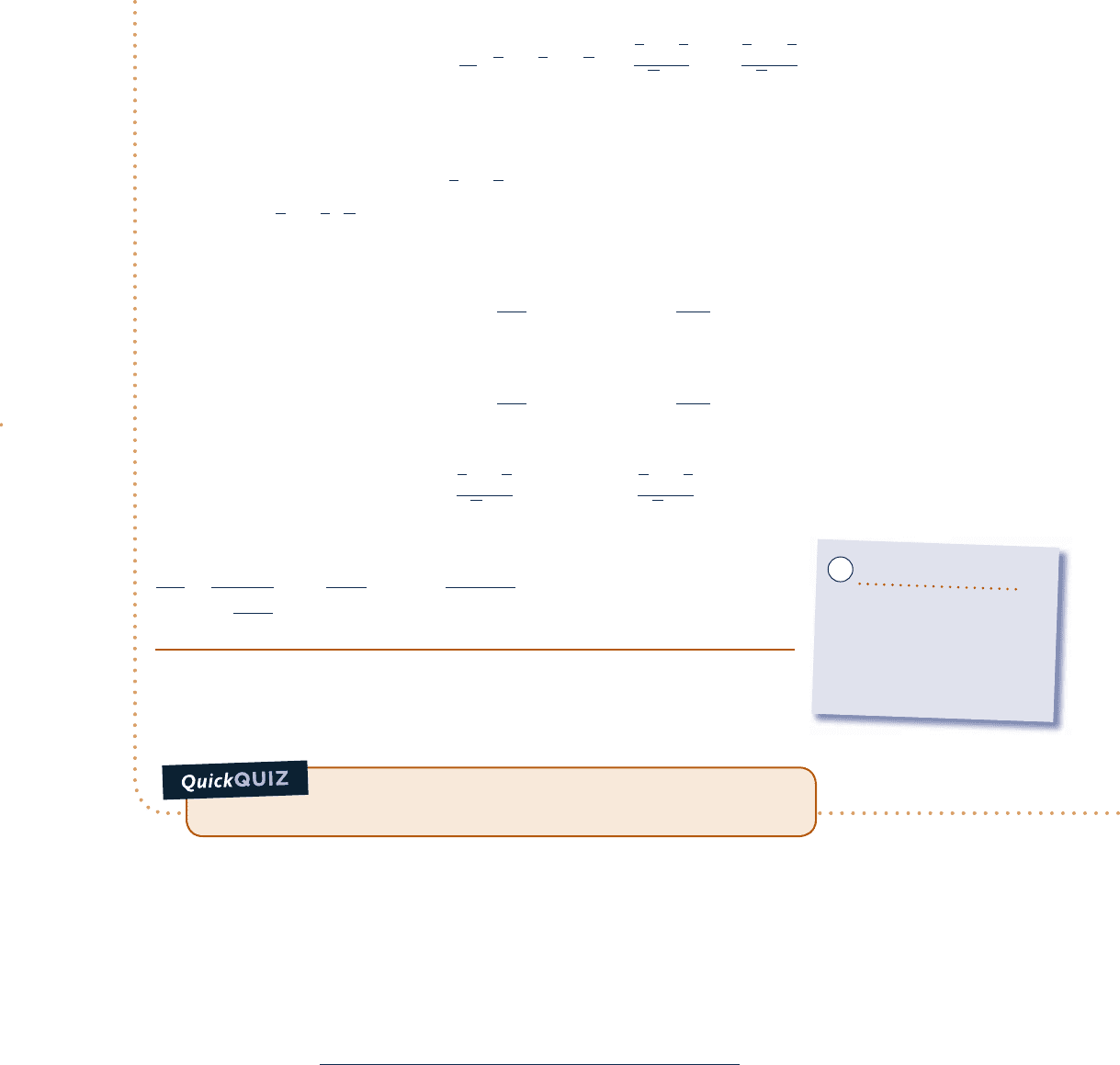
c c c c EXAMPLE 11.8 c

Nitrogen enters a turbine operating at steady state at 100 bar and 300 K and exits at 40 bar and 245 K. Using

the enthalpy departure chart, determine the work developed, in kJ per kg of nitrogen flowing, if heat transfer

with the surroundings can be ignored. Changes in kinetic and potential energy from inlet to exit also can be

neglected.

SOLUTION

Known:

A turbine operating at steady state has nitrogen entering at 100 bar and 300 K and exiting at 40 bar

and 245 K.

Find: Using the enthalpy departure chart, determine the work developed.

Schematic and Given Data:

= 100 bar

= 300 K

= 40 bar

= 245 K

–––

Fig. E11.8

Engineering Model:

The control volume shown on the accom-

panying figure operates at steady state.

2. There is no significant heat transfer between

the control volume and its surroundings.

3. Changes in kinetic and potential energy

between inlet and exit can be neglected.

4. Equilibrium property relations apply at the

inlet and exit.

Analysis: The mass and energy rate balances reduce at steady state to give

0 5

1 ch

2 h

2 V

1 g1z

2 z

where m

is the mass flow rate. Dropping the heat transfer term by assumption 2 and the kinetic and potential

energy terms by assumption 3 gives on rearrangement

5 h

2 h

EVALUATING ENTHALPY CHANGE. The change in specific enthalpy between

two states can be evaluated by expressing Eq. 11.80 in terms of the enthalpy departure as

2 h

5 h

2 h

2 RT

2 h

2 a

2 h

(11.85)

The first underlined term in Eq. 11.85 represents the change in specific enthalpy

between the two states assuming ideal gas behavior. The second underlined term is

the correction that must be applied to the ideal gas value for the enthalpy change to

obtain the actual value for the enthalpy change. Referring to the engineering litera-

ture, the quantity 1h

2 h2

at states 1 and 2 can be calculated with an equation

giving Z(T

, p

) or obtained from tables. This quantity also can be evaluated at state

1 from the generalized enthalpy departure chart, Fig. A-4, using the reduced tem-

perature T

and reduced pressure p

corresponding to the temperature T

and

pressure p

at the initial state, respectively. Similarly, 1h

2 h2

at state 2 can be

evaluated from Fig. A-4 using T

and p

. The use of Eq. 11.85 is illustrated in the

next example.

c11ThermodynamicRelations.indd Page 670 6/21/10 9:35:59 PM user-s146 c11ThermodynamicRelations.indd Page 670 6/21/10 9:35:59 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

Generalized Entropy Departure Chart

A generalized chart that allows changes in specific entropy to be evaluated can be

developed in a similar manner to the generalized enthalpy departure chart introduced

earlier in this section. The difference in specific entropy between states 1 and 2 of a

gas (or liquid) can be expressed as the identity

s1T

, p

22 s1T

, p

25 s

, p

22 s

, p

1 53s1T

, p

22 s

, p

242 3s1T

, p

22 s

, p

246 (11.86)

where

T, p

2 s

T, p

denotes the specific entropy of the substance relative to

that of its ideal gas model when both are at the same temperature and pressure.

Equation 11.86 indicates that the change in specific entropy between the two states

equals the entropy change determined using the ideal gas model plus a correction

(shown underlined) that accounts for the departure from ideal gas behavior. The ideal

gas term can be evaluated using methods introduced in Sec. 6.5. Let us consider next

how the correction term is evaluated in terms of the entropy departure.

The term h

2 h

can be evaluated as follows:

2 h

2 a

2 h

In this expression, M is the molecular weight of nitrogen and the other terms have the same significance as in

Eq. 11.85.

With specific enthalpy values from Table A-23 at T

5 300 K and T

5 245 K, respectively

2 h

5 8723 2 7121 5 1602 kJ

kmol

The terms

2 h

at states 1 and 2 required by the above expression for h

2 h

can be determined

from Fig. A-4. First, the reduced temperature and reduced pressure at the inlet and exit must be determined.

From Tables A-1, T

5 126 K, p

5 33.9 bar. Thus, at the inlet

300

5 2.38,



100

33.9

5 2.95

At the exit

245

5 1.94,



33.9

5 1.18

By inspection of Fig. A-4

➊

2 h

< 0.5,



2 h

< 0.31

Substituting values

kmol

c1602

kmol

2 a8.314

kmol ? K

b 1126 K210.5 2 0.312d5 50.1 kJ

➊ Due to inaccuracy in reading values from a graph such as Fig. A-4, we cannot

expect extreme accuracy in the final calculated result.

Ability to…

❑

use data from the generalized

enthalpy departure chart to

calculate the change in

enthalpy of nitrogen.

✓

Skills Developed

Determine the work developed, in kJ per kg of nitrogen flow-

ing, assuming the ideal gas model. Ans. 57.2 kJ/kg.

11.7 Generalized Charts for Enthalpy and Entropy 671

c11ThermodynamicRelations.indd Page 671 6/21/10 9:36:03 PM user-s146 c11ThermodynamicRelations.indd Page 671 6/21/10 9:36:03 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

672 Chapter 11 Thermodynamic Relations

DEVELOPING THE ENTROPY DEPARTURE. The following Maxwell relation

gives the variation of entropy with pressure at fixed temperature:

(11.35)

Integrating from pressure p9 to pressure p at fixed temperature T gives

s1T, p22 s1T, p¿252

p¿

(11.87)

For an ideal gas, y 5 RT/p, so

5 R

p. Using this in Eq. 11.87, the change

in specific entropy assuming ideal gas behavior is

1T, p22 s

1T, p¿252

p¿

(11.88)

Subtracting Eq. 11.88 from Eq. 11.87 gives

3s1T, p22 s

1T, p242 3s1T, p¿22 s

1T, p¿245

p¿

2 a

(11.89)

Since the properties of a substance tend to merge into those of its ideal gas model

as pressure tends to zero at fixed temperature, we have

lim

¿S0

3s1T, p¿22 s

1T, p¿245 0

Thus, in the limit as p9 tends to zero, Eq. 11.89 becomes

s1T, p22 s

1T, p25

2 a

d dp

(11.90)

Using p–y–T data only, Eq. 11.90 can be evaluated at states 1 and 2 and thus the

correction term of Eq. 11.86 evaluated.

Equation 11.90 can be expressed in terms of the compressibility factor Z and the

reduced properties T

and p

. The result, on a per mole basis, is the entropy departure

1T, p22 s1T, p2

1T22 h1T, p2

1Z 2 12

(11.91)

The right side of Eq. 11.91 depends only on the reduced temperature T

and

reduced pressure p

. Accordingly, the quantity

2 s

the entropy departure, is

a function only of these two reduced properties. As for the enthalpy departure, the

entropy departure can be evaluated with a computer using a generalized equation of

state giving Z as a function of T

and p

. Alternatively, tabular data from the litera-

ture or the graphical representation provided in Fig. A-5 can be employed.

EVALUATING ENTROPY CHANGE. The change in specific entropy between two

states can be evaluated by expressing Eq. 11.86 in terms of the entropy departure as

2 s

5 s

2 s

2 R ca

2 s

2 a

2 s

(11.92)

The first underlined term in Eq. 11.92 represents the change in specific entropy

between the two states assuming ideal gas behavior. The second underlined term is

the correction that must be applied to the ideal gas value for entropy change to

obtain the actual value for the entropy change. The quantity

2 s

R appearing in

Eq. 11.92 can be evaluated from the generalized entropy departure chart, Fig. A-5,

using the reduced temperature T

and reduced pressure p

corresponding to the

temperature T

and pressure p

at the initial state, respectively. Similarly,

2 s

entropy departure

c11ThermodynamicRelations.indd Page 672 6/21/10 9:36:06 PM user-s146 c11ThermodynamicRelations.indd Page 672 6/21/10 9:36:06 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New