Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics

Подождите немного. Документ загружается.

By comparison with Eq. 11.18, we conclude that

T 5 a

(11.24)

2p 5

(11.25)

The differential of the function h 5 h(s, p) is

dh 5 a

ds 1 a

By comparison with Eq. 11.19, we conclude that

T 5 a

(11.26)

y 5 a

(11.27)

Similarly, the coefficients 2p and 2s of Eq. 11.22 are partial derivatives of c(y, T)

2p 5 a

(11.28)

2s 5 a

(11.29)

and the coefficients y and 2s of Eq. 11.23 are partial derivatives of g(T, p)

y 5 a

(11.30)

2s 5 a

(11.31)

As each of the four differentials introduced above is exact, the second mixed partial

derivatives are equal. Thus, in Eq. 11.18, T plays the role of M in Eq. 11.14b and 2p

plays the role of N in Eq. 11.14b, so

52a

(11.32)

In Eq. 11.19, T and y play the roles of M and N in Eq. 11.14b, respectively. Thus

5 a

(11.33)

Similarly, from Eqs. 11.22 and 11.23 follow

5 a

(11.34)

52a

(11.35)

11.3 Developing Property Relations 643

c11ThermodynamicRelations.indd Page 643 6/21/10 9:34:05 PM user-s146c11ThermodynamicRelations.indd Page 643 6/21/10 9:34:05 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

644 Chapter 11 Thermodynamic Relations

Equations 11.32 through 11.35 are known as the Maxwell relations.

Since each of the properties T, p, y, s appears on the left side of two of the eight

equations, Eqs. 11.24 through 11.31, four additional property relations can be obtained

by equating such expressions. They are







(11.36)

Equations 11.24 through 11.36, which are listed in Table 11.1 for ease of reference,

are 16 property relations obtained from Eqs. 11.18, 11.19, 11.22, and 11.23, using the

concept of an exact differential. Since Eqs. 11.19, 11.22, and 11.23 can themselves be

derived from Eq. 11.18, the important role of the first T dS equation in developing

property relations is apparent.

The utility of these 16 property relations is demonstrated in subsequent sections

of this chapter. However, to give a specific illustration at this point, suppose the par-

tial derivative

involving entropy is required for a certain purpose. The Max-

well relation Eq. 11.34 would allow the derivative to be determined by evaluating the

partial derivative

, which can be obtained using p–y–T data only. Further

elaboration is provided in Example 11.3.

Maxwell relations

Summary of Property Relations from Exact Differentials

Basic relations:

from u 5 u(s, y) from h 5 h(s, p)

T 5 a

(11.24)

T 5 a

(11.26)

2p 5 a

(11.25)

y 5 a

(11.27)

from c 5 c(y, T) from g 5 g(T, p)

2p 5 a

(11.28)

y 5 a

(11.30)

2s 5 a

(11.29)

2s 5 a

(11.31)

Maxwell relations:

52a

(11.32)

5 a

(11.34)

5 a

(11.33)

52a

(11.35)

Additional relations:

5 a

(11.36)

5 a

TABLE 11.1

c11ThermodynamicRelations.indd Page 644 7/25/10 5:16:20 PM user-f391c11ThermodynamicRelations.indd Page 644 7/25/10 5:16:20 PM user-f391 /Users/user-f391/Desktop/Ramakant_25.07.10/Moran_JWCL314/New/Users/user-f391/Desktop/Ramakant_25.07.10/Moran_JWCL314/New

Applying the Maxwell Relations

c c c c EXAMPLE 11.3 c

Evaluate the partial derivative

for water vapor at a state fixed by a temperature of 2408C and a specific

volume of 0.4646 m

/kg. (a) Use the Redlich–Kwong equation of state and an appropriate Maxwell relation.

(b) Check the value obtained using steam table data.

SOLUTION

Known:

The system consists of a fixed amount of water vapor at 2408C and 0.4646 m

/kg.

Find: Determine the partial derivative

employing the Redlich–Kwong equation of state, together with

a Maxwell relation. Check the value obtained using steam table data.

Engineering Model:

The system consists of a fixed amount of water at a known equilibrium state.

2. Accurate values for

in the neighborhood of the given state can be determined from the Redlich–

Kwong equation of state.

Analysis:

(a)

The Maxwell relation given by Eq. 11.34 allows

to be determined from the p–y–T relationship. That is

The partial derivative 10p

0T2

obtained from the Redlich–Kwong equation, Eq. 11.7, is

y 2 b

2y1y 1 b2T

At the specified state, the temperature is 513 K and the specific volume on a molar basis is

y 5 0.4646

8.02 kg

kmol

b5 8.372

kmol

From Table A-24

a 5 142.59 bar

kmol

1K2



b 5 0.0211

kmol

Substituting values into the expression for

a8314

N ? m

kmol ? K

18.372 2 0.02112

142.59 bar a

kmol

1K2

8.372

8.3931

1513 K2

1 bar

1004.3

N ? m

? K

1 kJ

? m

5 1.0043

? K

Accordingly

5 1.0043

? K

(b) A value for

can be estimated using a graphical approach with steam table data, as follows: At 2408C,

Table A-4 provides the values for specific entropy s and specific volume y tabulated below

11.3 Developing Property Relations 645

c11ThermodynamicRelations.indd Page 645 6/22/10 7:30:07 PM user-s146c11ThermodynamicRelations.indd Page 645 6/22/10 7:30:07 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

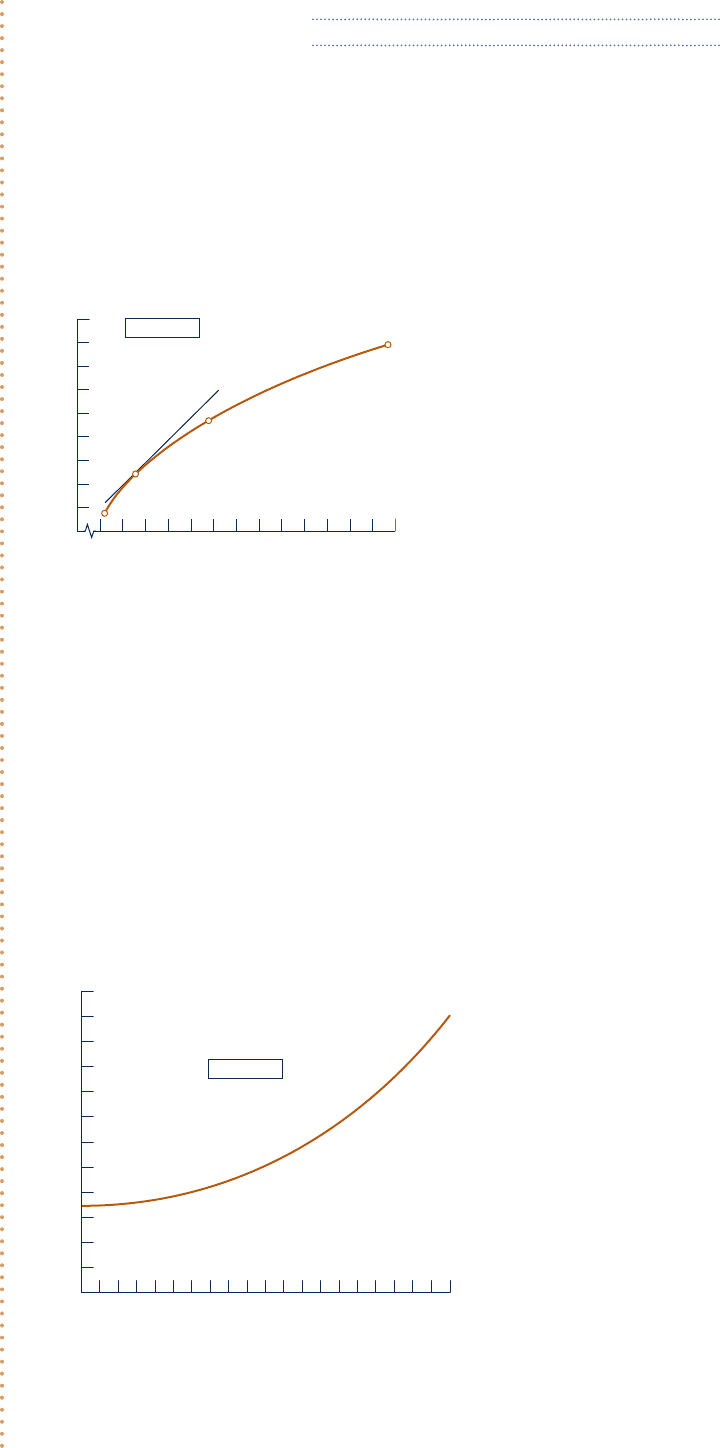
646 Chapter 11

Thermodynamic Relations

T 5 2408C

p (bar) s (kJ/kg ? K) y (m

/kg)

1.0 7.9949 2.359

1.5 7.8052 1.570

3.0 7.4774 0.781

5.0 7.2307 0.4646

7.0 7.0641 0.3292

10.0 6.8817 0.2275

With the values for s and y listed in the table, the plot in Fig. E11.3a giving s versus y can be prepared. Note

that a line representing the tangent to the curve at the given state is shown on the plot. The pressure at this

state is 5 bar. The slope of the tangent is

< 1.0 kJ

? K. Thus, the value of

obtained using the

Redlich–Kwong equation agrees closely with the result determined graphically using steam table data.

Alternative Solution: Alternatively, the partial derivative

can be estimated using numerical methods and com-

puter-generated data. The following IT code illustrates one way the partial derivative, denoted dsdv, can be estimated:

v 5 0.4646 // m

/kg

T 5 240 // 8C

v2 5 v 1 dv

v1 5 v 2 dv

dv 5 0.2

v2 5 v_PT (“Water/Steam”, p2, T)

v1 5 v_PT (“Water/Steam”, p1, T)

s2 5 s_PT (“Water/Steam”, p2, T)

s1 5 s_PT (“Water/Steam”, p1, T)

dsdv 5 (s2 2 s1)/(v2 2 v1)

Using the Explore button, sweep dv from 0.0001 to 0.2 in steps of 0.001. Then, using the Graph button, the fol-

lowing graph can be constructed:

Fig. E11.3a

T = 240°C

7.5

7.0

0.5

7 bar

5 bar

3 bar

1.5 bar

1.0

Specific volume, m

/kg

1.5

Specific entropy, kJ/kg·K

1.12

1.10

1.08

1.06

1.04

1.02

1.00

0.00 0.05 0.10

dsdv

0.15 0.20

T = 240°C

Fig. E11.3b

c11ThermodynamicRelations.indd Page 646 6/21/10 9:34:11 PM user-s146c11ThermodynamicRelations.indd Page 646 6/21/10 9:34:11 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

For steam at T 5 2408C, y 5 0.4646 m

/kg, p 5 5 bar, calcu-

late the value of the compressibility factor Z. Ans. 0.981.

From the computer data, the y-intercept of the graph is

➊

5 lim

¢yS0

¢s

¢y

< 1.033

? K

This answer is an estimate because it relies on a numerical approximation of

the partial derivative based on the equation of state that underlies the steam

tables. The values obtained using the Redlich–Kwong equation of state and the

graphical method using steam table data agree with this result.

➊ It is left as an exercise to show that, in accordance with Eq. 11.34, the value

estimated by a procedure like the one used for

agrees

with the value given here.

Ability to…

❑

apply a Maxwell relation to

evaluate a thermodynamic

quantity.

❑

apply the Redlich–Kwong

equation.

❑

perform a comparison with

data from the steam table

using graphical and

computer-based methods.

✓Skills Developed

11.3.3

Fundamental Thermodynamic Functions

A fundamental thermodynamic function provides a complete description of the ther-

modynamic state. In the case of a pure substance with two independent properties,

the fundamental thermodynamic function can take one of the following four forms:

u 5 u

s, y

h 5 h

s, p

(11.37)

c 5 c

T, y

g 5 g

T, p

Of the four fundamental functions listed in Eqs. 11.37, the Helmholtz function c

and the Gibbs function g have the greatest importance for subsequent discussions

(see Sec. 11.6.2). Accordingly, let us discuss the fundamental function concept with

reference to c and g.

In principle, all properties of interest can be determined from a fundamental ther-

modynamic function by differentiation and combination.

consider a fundamental function of the form c(T, y). The proper-

ties y and T, being the independent variables, are specified to fix the state. The pres-

sure p at this state can be determined from Eq. 11.28 by differentiation of c(T, y).

Similarly, the specific entropy s at the state can be found from Eq. 11.29 by differen-

tiation. By definition, c 5 u 2 Ts, so the specific internal energy is obtained as

u 5 c 1 Ts

With u, p, and y known, the specific enthalpy can be found from the definition

h 5 u 1 py. Similarly, the specific Gibbs function is found from the definition,

g 5 h 2 Ts. The specific heat c

can be determined by further differentiation,

. Other properties can be calculated with similar operations. b b b b b

consider a fundamental function of the form g(T, p). The proper-

ties T and p are specified to fix the state. The specific volume and specific entropy

at this state can be determined by differentiation from Eqs. 11.30 and 11.31, respec-

tively. By definition, g 5 h 2 Ts, so the specific enthalpy is obtained as

h 5

1 Ts

fundamental thermodynamic

function

11.3 Developing Property Relations 647

c11ThermodynamicRelations.indd Page 647 6/21/10 9:34:15 PM user-s146c11ThermodynamicRelations.indd Page 647 6/21/10 9:34:15 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

648 Chapter 11

Thermodynamic Relations

With h, p, and y known, the specific internal energy can be found from u 5 h 2 py.

The specific heat c

can be determined by further differentiation, c

. Other

properties can be calculated with similar operations. b b b b b

Like considerations apply for functions of the form u(s, y) and h(s, p), as can read-

ily be verified. Note that a Mollier diagram provides a graphical representation of

the fundamental function h(s, p).

11.4 Evaluating Changes in Entropy,

Internal Energy, and Enthalpy

With the introduction of the Maxwell relations, we are in a position to develop ther-

modynamic relations that allow changes in entropy, internal energy, and enthalpy to be

evaluated from measured property data. The presentation begins by considering relations

applicable to phase changes and then turns to relations for use in single-phase regions.

11.4.1

Considering Phase Change

The objective of this section is to develop relations for evaluating the changes in specific

entropy, internal energy, and enthalpy accompanying a change of phase at fixed tem-

perature and pressure. A principal role is played by the Clapeyron equation, which

allows the change in enthalpy during vaporization, sublimation, or melting at a constant

temperature to be evaluated from pressure-specific volume–temperature data pertain-

ing to the phase change. Thus, the present discussion provides important examples of

how p–y–T measurements can lead to the determination of other property changes,

namely Ds, Du, and Dh for a change of phase.

Consider a change in phase from saturated liquid to saturated vapor at fixed tem-

perature. For an isothermal phase change, pressure also remains constant, so Eq. 11.19

reduces to

dh 5 T ds

Integration of this expression gives

2 s

2 h

(11.38)

Hence, the change in specific entropy accompanying a phase change from saturated

liquid to saturated vapor at temperature T can be determined from the temperature

and the change in specific enthalpy.

The change in specific internal energy during the phase change can be determined

using the definition h 5 u 1 py.

2 u

5 h

2 h

2 p

2 y

(11.39)

Thus, the change in specific internal energy accompanying a phase change at tem-

perature T can be determined from the temperature and the changes in specific

volume and enthalpy.

CLAPEYRON EQUATION. The change in specific enthalpy required by Eqs.

11.38 and 11.39 can be obtained using the Clapeyron equation. To derive the Clap-

eyron equation, begin with the Maxwell relation

(11.34)

c11ThermodynamicRelations.indd Page 648 6/21/10 9:34:17 PM user-s146c11ThermodynamicRelations.indd Page 648 6/21/10 9:34:17 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

During a phase change at fixed temperature, the pressure is independent of specific

volume and is determined by temperature alone. Thus, the quantity

is deter-

mined by the temperature and can be represented as

sat

where “sat” indicates that the derivative is the slope of the saturation pressure–

temperature curve at the point determined by the temperature held constant during

the phase change (Sec. 11.2). Combining the last two equations gives

sat

Since the right side of this equation is fixed when the temperature is specified, the

equation can be integrated to give

2 s

sat

2 y

Introducing Eq. 11.38 into this expression results in the Clapeyron equation

sat

2 h

T1y

2 y

(11.40)

Equation 11.40 allows (h

2 h

) to be evaluated using only p–y–T data pertaining to

the phase change. In instances when the enthalpy change is also measured, the Clap-

eyron equation can be used to check the consistency of the data. Once the specific

enthalpy change is determined, the corresponding changes in specific entropy and

specific internal energy can be found from Eqs. 11.38 and 11.39, respectively.

Equations 11.38, 11.39, and 11.40 also can be written for sublimation or melting

occurring at constant temperature and pressure. In particular, the Clapeyron equation

would take the form

sat

h– 2 h¿

y– 2 y¿

(11.41)

where 0 and 9 denote the respective phases, and (dp/dT)

sat

is the slope of the relevant

saturation pressure–temperature curve.

The Clapeyron equation shows that the slope of a saturation line on a phase diagram

depends on the signs of the specific volume and enthalpy changes accompanying the

phase change. In most cases, when a phase change takes place with an increase in

specific enthalpy, the specific volume also increases, and (dp/dT)

sat

is positive. However,

in the case of the melting of ice and a few other substances, the specific volume decreases

on melting. The slope of the saturated solid–liquid curve for these few substances is

negative, as pointed out in Sec. 3.2.2 in the discussion of phase diagrams.

An approximate form of Eq. 11.40 can be derived when the following two idealiza-

tions are justified: (1) y

is negligible in comparison to y

, and (2) the pressure is low

enough that y

can be evaluated from the ideal gas equation of state as y

5 RT/p.

With these, Eq. 11.40 becomes

sat

2 h

which can be rearranged to read

d ln p

sat

2 h

(11.42)

Equation 11.42 is called the

Clausius–Clapeyron equation. A similar expression applies

for the case of sublimation.

Clapeyron equation

Clausius–Clapeyron

equation

11.4 Evaluating Changes in Entropy, Internal Energy, and Enthalpy 649

c11ThermodynamicRelations.indd Page 649 7/23/10 6:24:10 PM user-s146c11ThermodynamicRelations.indd Page 649 7/23/10 6:24:10 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

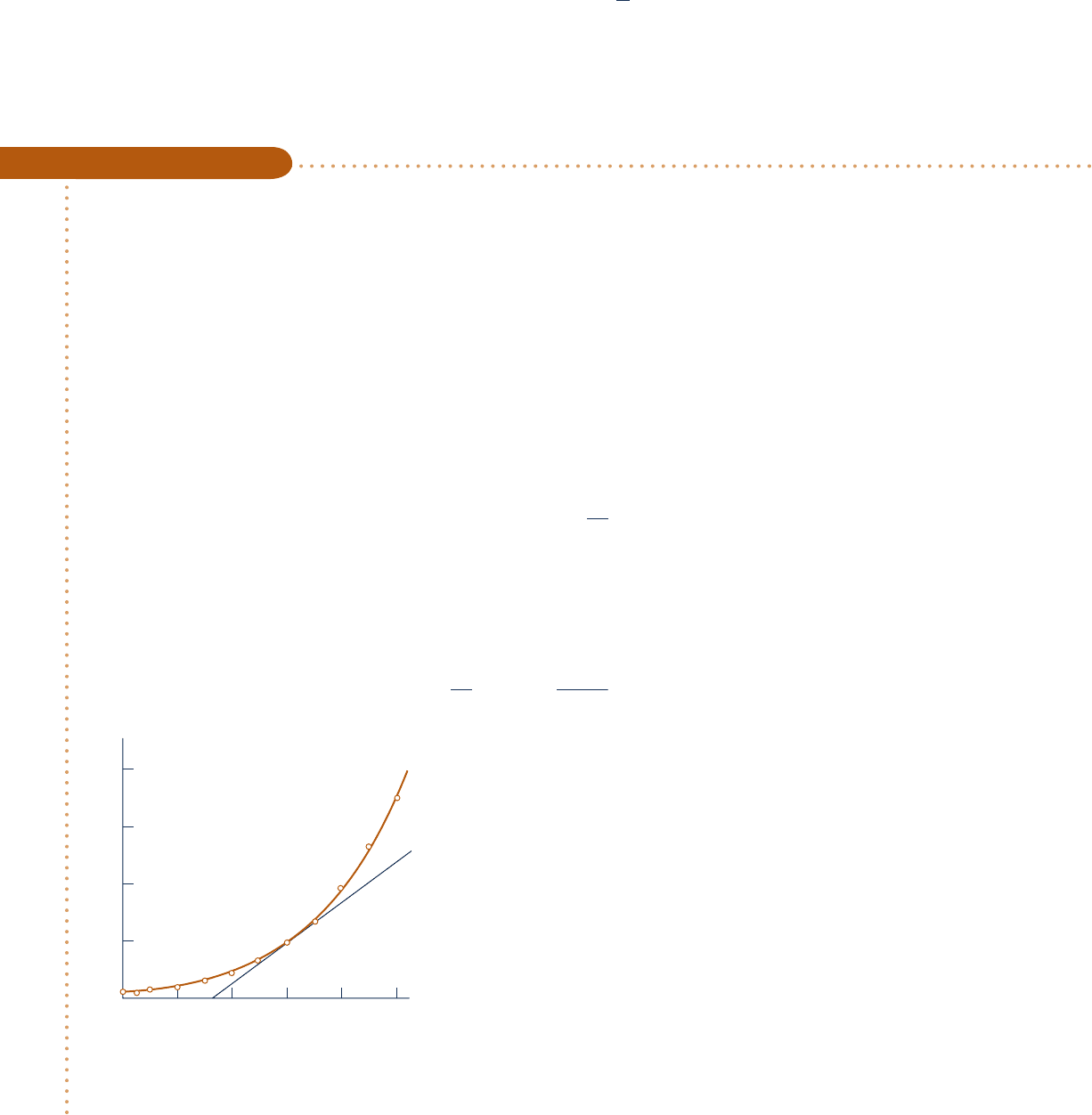
650 Chapter 11

Thermodynamic Relations

The use of the Clapeyron equation in any of the foregoing forms requires an accurate

representation for the relevant saturation pressure–temperature curve. This must not

only depict the pressure–temperature variation accurately but also enable accurate values

of the derivative (dp/dT)

sat

to be determined. Analytical representations in the form of

equations are commonly used. Different equations for different portions of the pressure–

temperature curves may be required. These equations can involve several constants. One

form that is used for the vapor-pressure curves is the four-constant equation

ln p

sat

5 A 1

1 C ln T 1 DT

in which the constants A, B, C, D are determined empirically.

The use of the Clapeyron equation for evaluating changes in specific entropy,

internal energy, and enthalpy accompanying a phase change at fixed T and p is illus-

trated in the next example.

Applying the Clapeyron Equation

c c c c EXAMPLE 11.4 c

Using p–y–T data for saturated water, calculate at 1008C (a) h

2 h

, (b) u

2 u

, (c) s

2 s

. Compare with the

respective steam table value.

SOLUTION

Known:

The system consists of a unit mass of saturated water at 1008C.

Find: Using saturation data, determine at 1008C the change on vaporization of the specific enthalpy, specific

internal energy, and specific entropy, and compare with the respective steam table value.

Analysis: For comparison, Table A-2 gives at 1008C, h

2 h

5 2257.0 kJ/kg, u

2 u

5 2087.6 kJ/kg, s

2 s

6.048 kJ/kg ? K.

(a) The value of h

2 h

can be determined from the Clapeyron equation, Eq. 11.40, expressed as

2 h

5 T1y

2 y

sat

This equation requires a value for the slope (dp/dT)

sat

of the saturation pressure–temperature curve at the

specified temperature.

The required value for (dp/dT)

sat

at 1008C can be estimated graphically as follows. Using saturation pressure–

temperature data from the steam tables, the accompanying plot can be prepared. Note that a line drawn tangent to

the curve at 1008C is shown on the plot. The slope of this tangent line is about 3570 N/m

? K. Accordingly, at 1008C

sat

< 3570

? K

Fig. E11.4

Saturation pressure (bar)

40 60 80 100 120 140

Temperature (°C)

c11ThermodynamicRelations.indd Page 650 6/21/10 9:34:18 PM user-s146c11ThermodynamicRelations.indd Page 650 6/21/10 9:34:18 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

Inserting property data from Table A-2 into the equation for h

2 h

gives

2 h

5 1373.15 K211.673 2 1.0435 3 10

b a3570

? K

1 kJ

N ? m

5 2227 kJ

This value is about 1% less than the value read from the steam tables.

➊ Alternatively, the derivative (dp/dT)

sat

can be estimated using numerical methods and computer-generated

data. The following IT code illustrates one way the derivative, denoted dpdT, can be estimated:

T 5 100 // 8C

dT 5 0.001

T1 5 T 2 dT

T2 5 T 1 dT

p1 5 Psat (“Water/Steam”, T1) // bar

p2 5 Psat (“Water/Steam”, T2) // bar

dpdT 5 ((p2 2 p1) / (T2 2 T1)) * 100000

Using the Explore button, sweep dT from 0.001 to 0.01 in steps of 0.001. Then, reading the limiting value from

the computer data

sat

< 3616

? K

When this value is used in the above expression for h

2 h

, the result is h

2 h

5 2256 kJ/kg, which agrees

closely with the value read from the steam tables.

(b) With Eq. 11.39

2 u

5 h

2 h

2 p

sat

2 y

Inserting the IT result for (h

2 h

) from part (a) together with saturation data at 1008C from Table A-2

2 u

5 2256

2 a1.014 3 10

b a1.672

1 kJ

N ? m

5 2086.5

which also agrees closely with the value from the steam tables.

2 h

) from part (a)

2 s

2 h

2256 kJ

373.15 K

5 6.046

? K

which again agrees closely with the steam table value.

➊ Also, (dp/dT)

sat

might be obtained by differentiating an analytical expres-

sion for the vapor pressure curve, as discussed on page 650.

Ability to…

❑

use the Clapeyron Equation

with p–y–T data for satu-

rated water to evaluate,

, h

, and s

❑

use graphical and computer-

based methods to evaluate

thermodynamic property

data and relations.

✓

Skills Developed

Use the IT result (dp/dT)

sat

5 3616 N/m

? K to extrapolate

the saturation pressure, in bar, at 1058C. Ans. 1.195 bar.

11.4.2

Considering Single-Phase Regions

The objective of the present section is to derive expressions for evaluating Ds, Du,

and Dh between states in single-phase regions. These expressions require both p–y–T

data and appropriate specific heat data. Since single-phase regions are under present

11.4 Evaluating Changes in Entropy, Internal Energy, and Enthalpy 651

c11ThermodynamicRelations.indd Page 651 6/21/10 9:34:21 PM user-s146c11ThermodynamicRelations.indd Page 651 6/21/10 9:34:21 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

652 Chapter 11

Thermodynamic Relations

consideration, any two of the properties pressure, specific volume, and temperature

can be regarded as the independent properties that fix the state. Two convenient

choices are T, y and T, p.

T AND y AS INDEPENDENT PROPERTIES. With temperature and specific

volume as the independent properties that fix the state, the specific entropy can be

regarded as a function of the form s 5 s(T, y). The differential of this function is

ds 5 a

dT 1 a

The partial derivative

appearing in this expression can be replaced using the

Maxwell relation, Eq. 11.34, giving

ds 5 a

dT 1 a

(11.43)

The specific internal energy also can be regarded as a function of T and y: u 5

u(T, y). The differential of this function is

du 5 a

dT 1 a

With c

5 10u

0T2

du 5 c

dT 1 a

(11.44)

Substituting Eqs. 11.43 and 11.44 into du 5 T ds 2 p dy and collecting terms

results in

1 p 2 T a

ddy 5 cT a

2 c

ddT

(11.45)

Since specific volume and temperature can be varied independently, let us hold spe-

cific volume constant and vary temperature. That is, let dy 5 0 and

ﬁ

. It then

follows from Eq. 11.45 that

(11.46)

Similarly, suppose that dT 5 0 and

dy ? 0

. It then follows that

5 T

2 p

(11.47)

Equations 11.46 and 11.47 are additional examples of useful thermodynamic prop-

erty relations.

Equation 11.47, which expresses the dependence of the specific

internal energy on specific volume at fixed temperature, allows us to demonstrate

that the internal energy of a gas whose equation of state is py 5 RT depends on

temperature alone, a result first discussed in Sec. 3.12.2. Equation 11.47 requires the

partial derivative

. If p 5 RT/y, the derivative is

5 R

y. Introducing

this, Eq. 11.47 gives

5 T

2 p 5 T

2 p 5 p 2 p 5 0

This demonstrates that when py 5 RT, the specific internal energy is independent of

specific volume and depends on temperature alone.

b b b b b

TAKE NOTE...

Here we demonstrate that

the specific internal energy

of a gas whose equation of

state is

py 5 RT

depends on temperature

alone, thereby confirming a

claim made in Sec. 3.12.2.

c11ThermodynamicRelations.indd Page 652 6/21/10 9:34:24 PM user-s146c11ThermodynamicRelations.indd Page 652 6/21/10 9:34:24 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New