Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics

Подождите немного. Документ загружается.

for gases, but some describe the p–y–T behavior of the liquid phase, at least qual-

itatively. Every equation of state is restricted to particular states. This realm of

applicability is often indicated by giving an interval of pressure, or density, where

the equation can be expected to represent the p–y–T behavior faithfully. When it

is not stated, the realm of applicability of a given equation can be approximated

by expressing the equation in terms of the compressibility factor Z and the

reduced properties p

, T

, y9

and superimposing the result on a generalized com-

pressibility chart or comparing with tabulated compressibility data obtained from

the literature.

11.1.2

Two-Constant Equations of State

Equations of state can be classified by the number of adjustable constants they

include. Let us consider some of the more commonly used equations of state in order

of increasing complexity, beginning with two-constant equations of state.

van der Waals Equation

An improvement over the ideal gas equation of state based on elementary molecular

arguments was suggested in 1873 by van der Waals, who noted that gas molecules

actually occupy more than the negligibly small volume presumed by the ideal gas

model and also exert long-range attractive forces on one another. Thus, not all of the

volume of a container would be available to the gas molecules, and the force they

exert on the container wall would be reduced because of the attractive forces that

exist between molecules. Based on these elementary molecular arguments, the van der

Waals equation of state

p 5

2 b

(11.2)

The constant b is intended to account for the finite volume occupied by the molecules,

the term a

accounts for the forces of attraction between molecules, and

is the

universal gas constant. Note than when a and b are set to zero, the ideal gas equation

of state results.

The van der Waals equation gives pressure as a function of temperature and spe-

cific volume and thus is explicit in pressure. Since the equation can be solved for

temperature as a function of pressure and specific volume, it is also explicit in tem-

perature. However, the equation is cubic in specific volume, so it cannot gen-

erally be solved for specific volume in terms of temperature and pressure. The

van der Waals equation is not explicit in specific volume.

EVALUATING a AND b. The van der Waals equation is a two-constant

equation of state. For a specified substance, values for the constants a and b

can be found by fitting the equation to p–y–T data. With this approach sev-

eral sets of constants might be required to cover all states of interest. Alter-

natively, a single set of constants for the van der Waals equation can be

determined by noting that the critical isotherm passes through a point of

inflection at the critical point, and the slope is zero there. Expressed math-

ematically, these conditions are, respectively

5 0,



5 0



1critical point2

(11.3)

Although less overall accuracy normally results when the constants a and b

are determined using critical point behavior than when they are determined

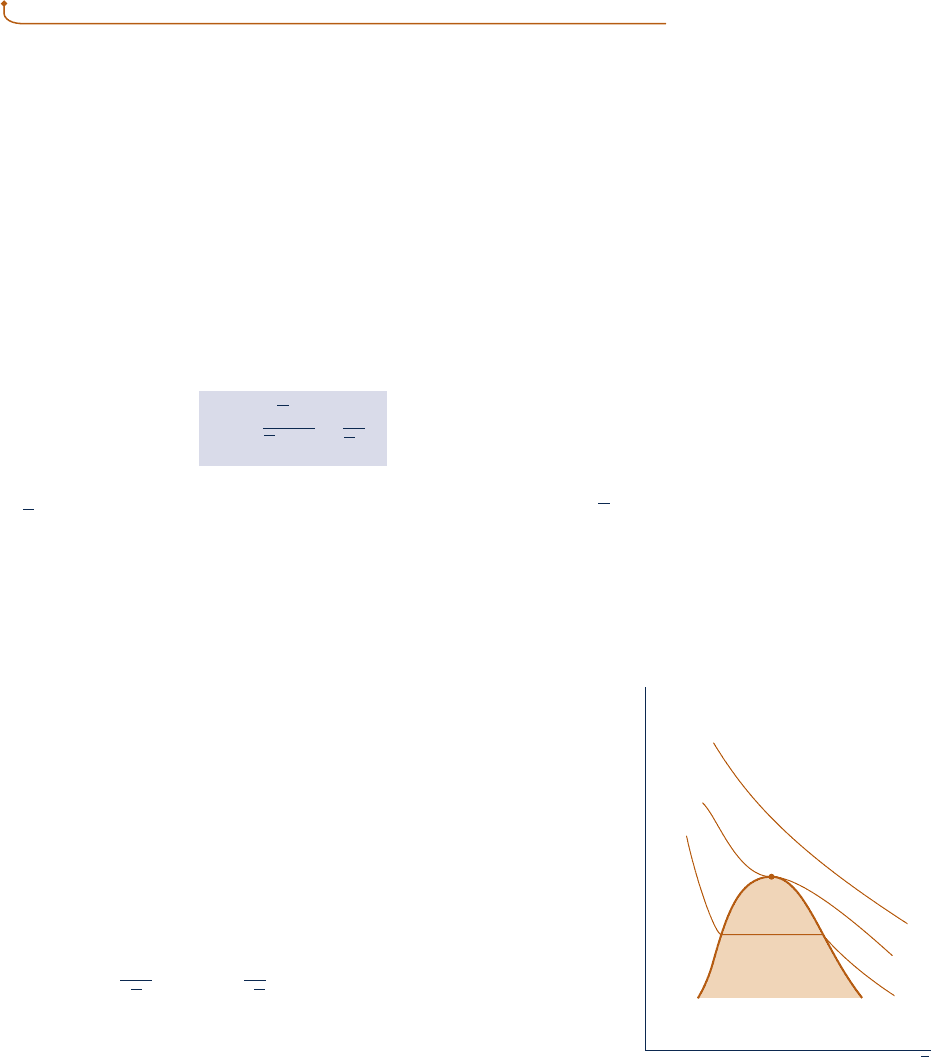
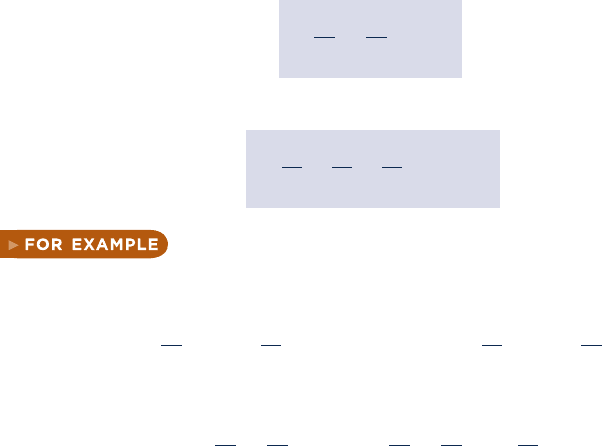
van der Waals equation

∂p

–––

∂v

(

= 0

T < T

T = T

T > T

Critical

point

11.1 Using Equations of State 633

c11ThermodynamicRelations.indd Page 633 6/21/10 9:33:41 PM user-s146c11ThermodynamicRelations.indd Page 633 6/21/10 9:33:41 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

634 Chapter 11

Thermodynamic Relations

by fitting p–y–T data in a particular region of interest, the advantage of this approach

is that the van der Waals constants can be expressed in terms of the critical pressure

and critical temperature T

, as demonstrated next.

For the van der Waals equation at the critical point

2 b

Applying Eqs. 11.3 with the van der Waals equation gives

2 b2

5 0

5 2

2 b

5 0

Solving the foregoing three equations for a, b, and y

in terms of the critical pressure

and critical temperature

a 5

(11.4a)

b 5

(11.4b)

(11.4c)

Values of the van der Waals constants a and b determined from Eqs. 11.4a and 11.4b

for several common substances are given in Table A-24 for pressure in bar, specific

volume in m

/kmol, and temperature in K. Values of a and b for the same substances

are given in Table A-24E for pressure in atm, specific volume in ft

/lbmol, and tem-

perature in 8R.

GENERALIZED FORM. Introducing the compressibility factor Z 5

RT, the

reduced temperature T

5 T/T

, the pseudoreduced specific volume y¿

5 p

and the foregoing expressions for a and b, the van der Waals equation can be written

in terms of Z, y9

, and T

Z 5

y¿

2 1

y¿

(11.5)

or alternatively in terms of Z, T

, and p

2 a

1 1bZ

1 a

27p

64T

bZ 2

27p

512T

5 0

(11.6)

The details of these developments are left as exercises. Equation 11.5 can be evalu-

ated for specified values of y9

and T

and the resultant Z values located on a gen-

eralized compressibility chart to show approximately where the equation performs

satisfactorily. A similar approach can be taken with Eq. 11.6.

The compressibility factor at the critical point yielded by the van der Waals equa-

tion is determined from Eq. 11.4c as

5 0.375

Actually, Z

varies from about 0.23 to 0.33 for most substances (see Tables A-1).

Accordingly, with the set of constants given by Eqs. 11.4, the van der Waals equation

is inaccurate in the vicinity of the critical point. Further study would show inaccuracy

in other regions as well, so this equation is not suitable for many thermodynamic

evaluations. The van der Waals equation is of interest to us primarily because it is

c11ThermodynamicRelations.indd Page 634 7/25/10 5:15:21 PM user-f391c11ThermodynamicRelations.indd Page 634 7/25/10 5:15:21 PM user-f391 /Users/user-f391/Desktop/Ramakant_25.07.10/Moran_JWCL314/New/Users/user-f391/Desktop/Ramakant_25.07.10/Moran_JWCL314/New

the simplest model that accounts for the departure of actual gas behavior from the

ideal gas equation of state.

Redlich–Kwong Equation

Three other two-constant equations of state that have been widely used are the Berthelot,

Dieterici, and Redlich–Kwong equations. The Redlich–Kwong equation, considered by

many to be the best of the two-constant equations of state, is

p 5

y 2 b

y 1 b

(11.7)

This equation, proposed in 1949, is mainly empirical in nature, with no rigorous jus-

tification in terms of molecular arguments. The Redlich–Kwong equation is explicit

in pressure but not in specific volume or temperature. Like the van der Waals equa-

tion, the Redlich–Kwong equation is cubic in specific volume.

Although the Redlich–Kwong equation is somewhat more difficult to manipulate

mathematically than the van der Waals equation, it is more accurate, particularly at

higher pressures. The two-constant Redlich–Kwong equation performs better than

some equations of state having several adjustable constants; still, two-constant equa-

tions of state tend to be limited in accuracy as pressure (or density) increases. Increased

accuracy at such states normally requires equations with a greater number of adjust-

able constants. Modified forms of the Redlich–Kwong equation have been proposed

to achieve improved accuracy.

EVALUATING a AND b. As for the van der Waals equation, the constants a and

b in Eq. 11.7 can be determined for a specified substance by fitting the equation to

p–y–T data, with several sets of constants required to represent accurately all states

of interest. Alternatively, a single set of constants in terms of the critical pressure and

critical temperature can be evaluated using Eqs. 11.3, as for the van der Waals equa-

tion. The result is

a 5 a¿

and

b 5 b¿

(11.8)

where a9 5 0.42748 and b9 5 0.08664. Evaluation of these constants is left as an

exercise. Values of the Redlich–Kwong constants a and b determined from Eqs. 11.8

for several common substances are given in Table A-24 for pressure in bar, specific

volume in m

/kmol, and temperature in K. Values of a and b for the same substances

are given in Table A-24E for pressure in atm, specific volume in ft

/lbmol, and tem-

perature in 8R.

GENERALIZED FORM. Introducing the compressibility factor Z, the reduced

temperature T

, the pseudoreduced specific volume y9

, and the foregoing expressions

for a and b, the Redlich–Kwong equation can be written as

Z 5

y¿

2 b¿

a¿

y¿

1 b¿

(11.9)

Equation 11.9 can be evaluated at specified values of y9

and T

and the resultant Z

values located on a generalized compressibility chart to show the regions where the

equation performs satisfactorily. With the constants given by Eqs. 11.8, the com-

pressibility factor at the critical point yielded by the Redlich–Kwong equation is

5 0.333, which is at the high end of the range of values for most substances,

indicating that inaccuracy in the vicinity of the critical point should be expected.

In Example 11.1, the pressure of a gas is determined using three equations of state

and the generalized compressibility chart. The results are compared.

Redlich–Kwong equation

11.1 Using Equations of State 635

c11ThermodynamicRelations.indd Page 635 6/21/10 9:33:46 PM user-s146c11ThermodynamicRelations.indd Page 635 6/21/10 9:33:46 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

636 Chapter 11

Thermodynamic Relations

Comparing Equations of State

c c c c EXAMPLE 11.1 c

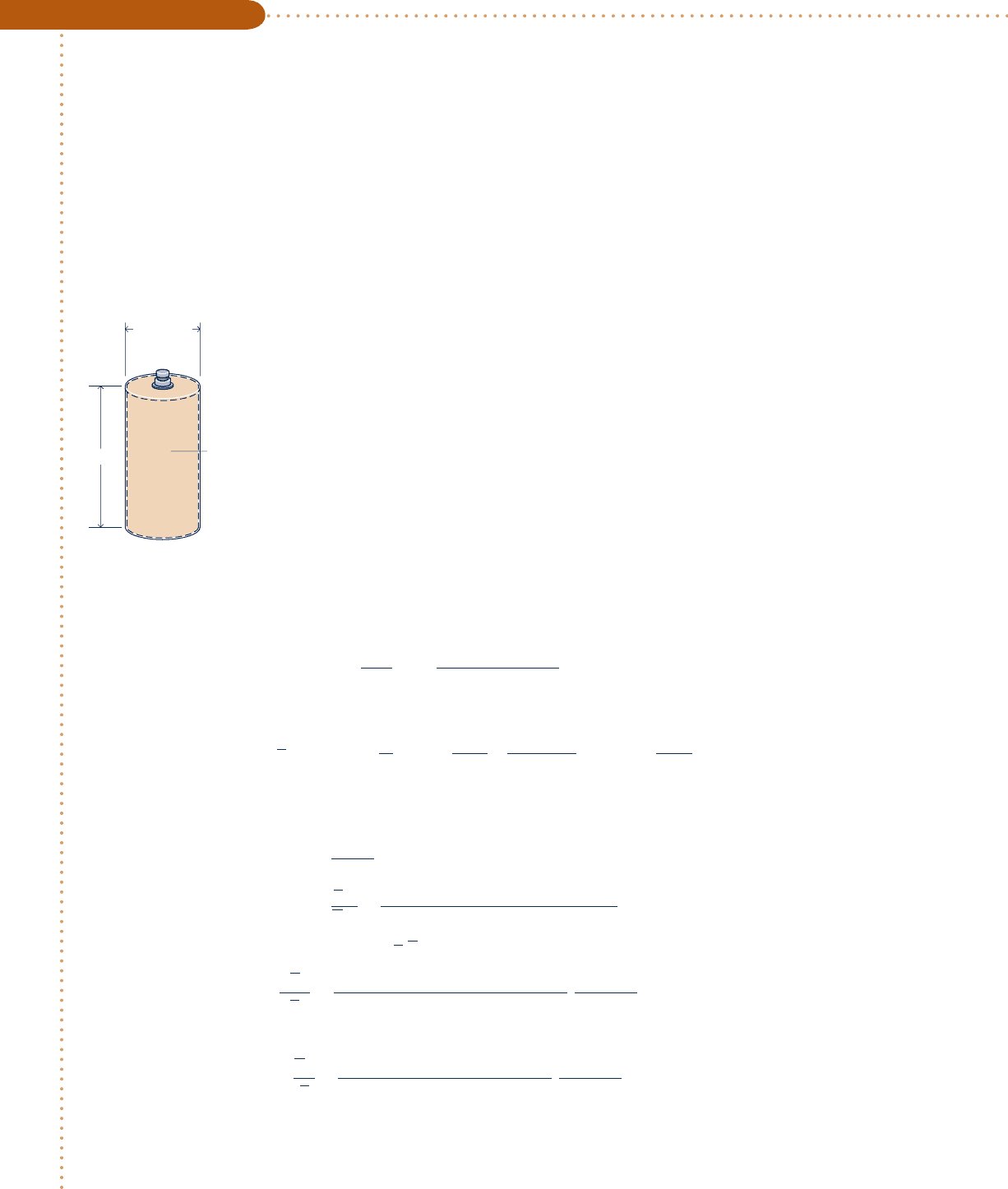
A cylindrical tank containing 4.0 kg of carbon monoxide gas at 2508C has an inner diameter of 0.2 m and a

length of 1 m. Determine the pressure, in bar, exerted by the gas using (a) the generalized compressibility chart,

(b) the ideal gas equation of state, (c) the van der Waals equation of state, (d) the Redlich–Kwong equation of

state. Compare the results obtained.

SOLUTION

Known:

A cylindrical tank of known dimensions contains 4.0 kg of CO gas at 2508C.

Find: Determine the pressure exerted by the gas using four alternative methods.

Schematic and Given Data:

Analysis: The molar specific volume of the gas is required in each part of the solution. Let us begin by evaluat-

ing it. The volume occupied by the gas is

V 5

L 5

p10.2 m2

11.0 m2

5 0.0314 m

The molar specific volume is then

y 5 My 5 M a

b5 a28

kmol

b a

0.0314 m

4.0 kg

b5 0.2198

kmol

(a) From Table A-1 for CO, T

5 133 K, p

5 35 bar. Thus, the reduced temperature T

and pseudoreduced

specific volume y9

are, respectively

223 K

133 K

5 1.68

y¿

10.2198 m

kmol2135 3 10

18314 N ? m

kmol ? K21133 K2

5 0.696

Turning to Fig. A-2, Z < 0.9. Solving Z 5 py

RT for pressure and inserting known values

p 5

ZRT

0.918314 N ? m

kmol ? K21223 K2

10.2198 m

kmol2

1 bar

`5 75.9 bar

(b) The ideal gas equation of state gives

p 5

18314 N ? m

kmol ? K21223 K2

10.2198 m

kmol2

1 bar

`5 84.4 bar

Fig. E11.1

D = 0.2 m

= 1 m

4 kg CO gas

at –50°C

Engineering Model:

As shown in the accompanying figure, the closed system is taken as the gas.

2. The system is at equilibrium.

c11ThermodynamicRelations.indd Page 636 6/21/10 9:33:47 PM user-s146c11ThermodynamicRelations.indd Page 636 6/21/10 9:33:47 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

11.1.3

Multiconstant Equations of State

To fit the p–y–T data of gases over a wide range of states, Beattie and Bridgeman pro-

posed in 1928 a pressure-explicit equation involving five constants in addition to the gas

constant. The Beattie–Bridgeman equation can be expressed in a truncated virial form as

p 5

(11.10)

where

b 5 BRT 2 A 2 cR

g 52BbRT 1 Aa 2 BcR

d 5 BbcR

(11.11)

Beattie–Bridgeman

equation

Table A-24. Thus

a 5 1.474 bara

kmol



and



b 5 0.0395

kmol

Substituting into Eq. 11.2

y 2 b

18314 N ? m

kmol ? K21223 K2

10.2198 2 0.039521m

kmol2

1 bar

1.474 bar1m

kmol2

10.2198 m

kmol2

5 72.3 bar

Alternatively, the values for y9

and T

obtained in the solution of part (a) can be substituted into Eq. 11.5, giv-

ing Z 5 0.86. Then, with p 5 ZRT

y, p 5 72.5 bar. The slight difference is attributed to roundoff.

(d) For carbon monoxide, the Redlich–Kwong constants given by Eqs. 11.8 can be read directly from Table

A-24. Thus

a 5

17.22 bar1m

21K2

1kmol2



and



b 5 0.02737 m

kmol

Substituting into Eq. 11.7

y 2 b

y 1 b

18314 N ? m

kmol ? K21223 K2

10.2198 2 0.027372 m

kmol

1 bar

17.22 bar

10.2198210.24717212232

5 75.1 bar

Alternatively, the values for y9

and T

obtained in the solution of part (a) can

be substituted into Eq. 11.9, giving Z 5 0.89. Then, with p 5 ZRT

y, p 5 75.1

bar. In comparison to the value of part (a), the ideal gas equation of state

predicts a pressure that is 11% higher and the van der Waals equation gives a

value that is 5% lower. The Redlich–Kwong value is about 1% less than the

value obtained using the compressibility chart.

Using the given temperature and the pressure value deter-

mined in part (a), check the value of Z using Fig. A-2. Ans. Z

0.9.

Ability to…

❑

determine pressure using

the compressibility chart,

ideal gas model, and the

van der Waals and Redlich–

Kwong equations of state.

❑

perform unit conversions

correctly.

✓

Skills Developed

11.1 Using Equations of State 637

c11ThermodynamicRelations.indd Page 637 6/22/10 7:29:51 PM user-s146c11ThermodynamicRelations.indd Page 637 6/22/10 7:29:51 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

638 Chapter 11

Thermodynamic Relations

The five constants a, b, c, A, and B appearing in these equations are determined by

curve fitting to experimental data.

Benedict, Webb, and Rubin extended the Beattie–Bridgeman equation of state to

cover a broader range of states. The resulting equation, involving eight constants in

addition to the gas constant, has been particularly successful in predicting the p–y–T

behavior of light hydrocarbons. The Benedict–Webb–Rubin equation is

p 5

1 aBRT 2 A 2

RT 2 a2

a1 1

bexp a2

(11.12)

Values of the constants appearing in Eq. 11.12 for five common substances are given in

Table A-24 for pressure in bar, specific volume in m

/kmol, and temperature in K. Values

of the constants for the same substances are given in Table A-24E for pressure in atm,

specific volume in ft

/lbmol, and temperature in 8R. Because Eq. 11.12 has been so suc-

cessful, its realm of applicability has been extended by introducing additional constants.

Equations 11.10 and 11.12 are merely representative of multiconstant equations of

state. Many other multiconstant equations have been proposed. With high-speed com-

puters, equations having 50 or more constants have been developed for representing

the p–y–T behavior of different substances.

11.2 Important Mathematical Relations

Values of two independent intensive properties are sufficient to fix the intensive state

of a simple compressible system of specified mass and composition—for instance, tem-

perature and specific volume (see Sec. 3.1). All other intensive properties can be deter-

mined as functions of the two independent properties: p 5 p(T, y), u 5 u(T, y), h 5

h(T, y), and so on. These are all functions of two independent variables of the form

z 5 z (x, y), with x and y being the independent variables. It might also be recalled

that the differential of every property is exact (Sec. 2.2.1). The differentials of nonprop-

erties such as work and heat are inexact. Let us review briefly some concepts from

calculus about functions of two independent variables and their differentials.

The exact differential of a function z, continuous in the variables x and y, is

dz 5 a

dx 1 a

(11.13a)

This can be expressed alternatively as

dz 5 M dx 1 N dy (11.13b)

where M 5 10z

0x2

and N 5 10z

0y2

. The coefficient M is the partial derivative of z

with respect to x (the variable y being held constant). Similarly, N is the partial

derivative of z with respect to y (the variable x being held constant).

If the coefficients M and N have continuous first partial derivatives, the order in

which a second partial derivative of the function z is taken is immaterial. That is

(11.14a)

5 a

(11.14b)

which can be called the test for exactness, as discussed next.

Benedict–Webb–Rubin

equation

exact differential

TAKE NOTE...

The state principle for

simple systems is intro-

duced in Sec. 3.1.

test for exactness

c11ThermodynamicRelations.indd Page 638 6/21/10 9:33:57 PM user-s146c11ThermodynamicRelations.indd Page 638 6/21/10 9:33:57 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

In words, Eqs. 11.14 indicate that the mixed second partial derivatives of the func-

tion z are equal. The relationship in Eqs. 11.14 is both a necessary and sufficient

condition for the exactness of a differential expression, and it may therefore be used

as a test for exactness. When an expression such as M dx 1 N dy does not meet this

test, no function z exists whose differential is equal to this expression. In thermody-

namics, Eq. 11.14 is not generally used to test exactness but rather to develop addi-

tional property relations. This is illustrated in Sec. 11.3 to follow.

Two other relations among partial derivatives are listed next for which applications

are found in subsequent sections of this chapter. These are

5 1

(11.15)

and

521

(11.16)

consider the three quantities x, y, and z, any two of which may

be selected as the independent variables. Thus, we can write x 5 x(y, z) and y 5 y(x, z).

The differentials of these functions are, respectively

dx 5 a

dy 1 a

dz and dy 5 a

dx 1 a

Eliminating dy between these two equations results in

c1 2 a

ddx 5 ca

1 a

ddz

(11.17)

Since x and z can be varied independently, let us hold z constant and vary x. That is,

let dz 5 0 and dx ? 0. It then follows from Eq. 11.17 that the coefficient of dx must

vanish, so Eq. 11.15 must be satisfied. Similarly, when dx 5 0 and

dz ? 0

, the coeffi-

cient of dz in Eq. 11.17 must vanish. Introducing Eq. 11.15 into the resulting expression

and rearranging gives Eq. 11.16. The details are left as an exercise. b b b b b

APPLICATION. An equation of state p 5 p(T, y) provides a specific example of

a function of two independent variables. The partial derivatives

and

of p(T, y) are important for subsequent discussions. The quantity

is the partial

derivative of p with respect to T (the variable y being held constant). This partial

derivative represents the slope at a point on a line of constant specific volume (isomet-

ric) projected onto the p–T plane. Similarly, the partial derivative

is the partial

derivative of p with respect to y (the variable T being held constant). This partial

derivative represents the slope at a point on a line of constant temperature (isotherm)

projected on the p–y plane. The partial derivatives

and

are themselves

intensive properties because they have unique values at each state.

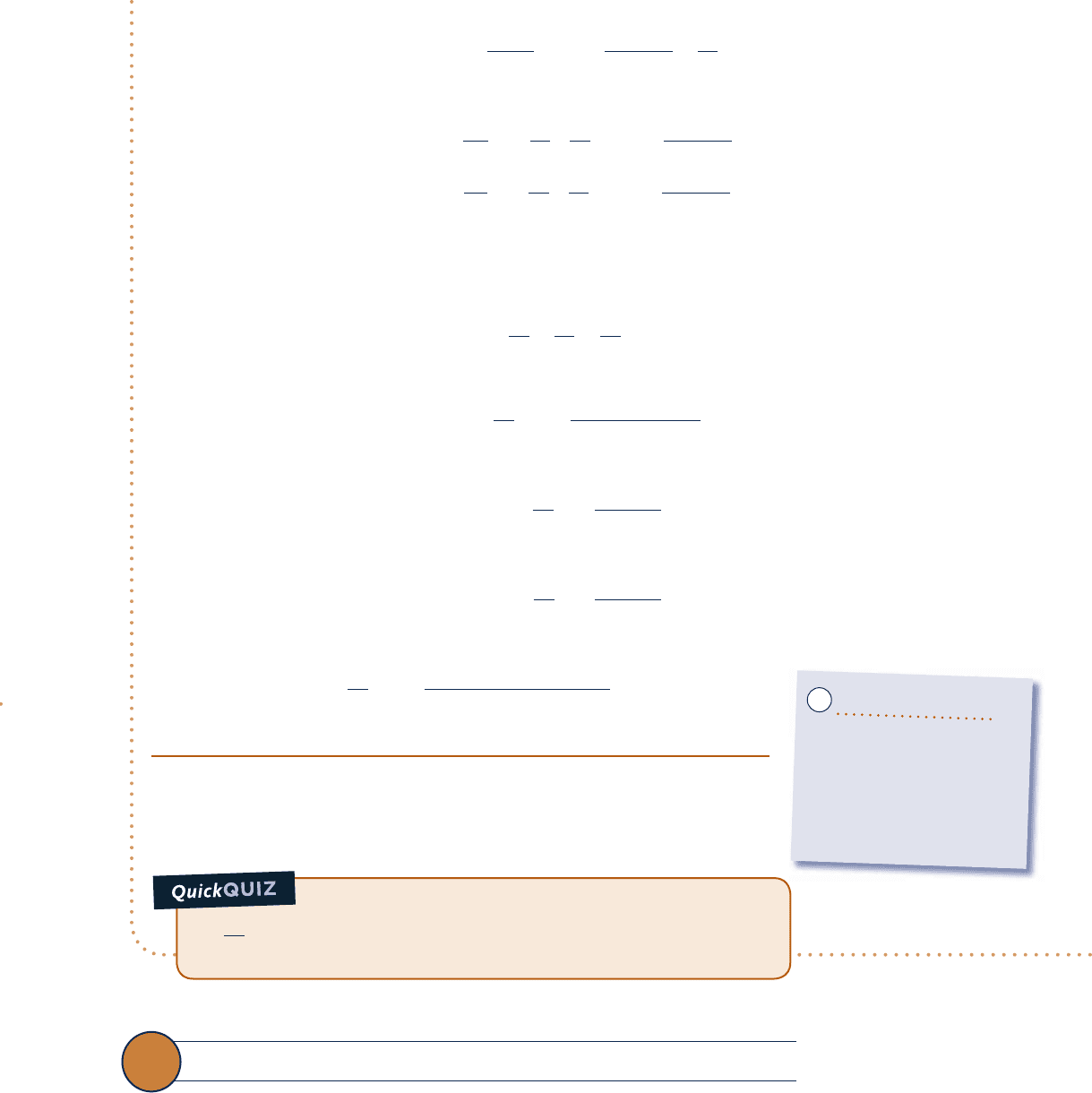
The p–y–T surfaces given in Figs. 3.1 and 3.2 are graphical representations of func-

tions of the form p 5 p(y, T). Figure 11.1 shows the liquid, vapor, and two-phase

regions of a p–y–T surface projected onto the p–y and p–T planes. Referring first to

Fig. 11.1a, note that several isotherms are sketched. In the single-phase regions, the

partial derivative

giving the slope is negative at each state along an isotherm

except at the critical point, where the partial derivative vanishes. Since the isotherms

are horizontal in the two-phase liquid–vapor region, the partial derivative

vanishes there as well. For these states, pressure is independent of specific volume

and is a function of temperature only: p 5 p

sat

(T ).

Figure 11.1b shows the liquid and vapor regions with several isometrics (constant

specific volume lines) superimposed. In the single-phase regions, the isometrics are

11.2 Important Mathematical Relations 639

c11ThermodynamicRelations.indd Page 639 6/21/10 9:33:58 PM user-s146c11ThermodynamicRelations.indd Page 639 6/21/10 9:33:58 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

640 Chapter 11

Thermodynamic Relations

nearly straight or are slightly curved and the partial derivative 10p

0T2

is positive at

each state along the curves. For the two-phase liquid–vapor states corresponding to

a specified value of temperature, the pressure is independent of specific volume and

is determined by the temperature only. Hence, the slopes of isometrics passing through

the two-phase states corresponding to a specified temperature are all equal, being

given by the slope of the saturation curve at that temperature, denoted simply as

(dp/dT)

sat

. For these two-phase states, 10p

0T2

5 1dp

dT2

sat

In this section, important aspects of functions of two variables have been intro-

duced. The following example illustrates some of these ideas using the van der Waals

equation of state.

)

(b)

Critical

point

Liquid

Triple

point

Locus of saturation states

Vapor

Isometric

v < v

v = v

v > v

∂p

–––

∂T

(

> 0

∂p

–––

∂v

(

< 0

∂p

–––

∂v

(

= 0

∂p

–––

∂v

(

< 0

∂p

–––

∂T

(

> 0

–––

(

sat

T < T

T = T

T > T

Isotherm

Critical

point

(∂p/∂v)

= 0

Liquid-vapor

Fig. 11.1 Diagrams used to discuss (≠p/≠

)

and (≠p/≠T)

. (a) p–

diagram. (b) Phase diagram.

Applying Mathematical Relations

c c c c EXAMPLE 11.2 c

For the van der Waals equation of state, (a) determine an expression for the exact differential dp, (b) show that

the mixed second partial derivatives of the result obtained in part (a) are equal, and (c) develop an expression

for the partial derivative 10y

0T2

SOLUTION

Known:

The equation of state is the van der Waals equation.

Find: Determine the differential dp, show that the mixed second partial derivatives of dp are equal, and develop

an expression for 10y

0T2

Analysis:

(a)

By definition, the differential of a function p 5 p(T, y) is

dp 5 a

dT 1 a

The partial derivatives appearing in this expression obtained from the van der Waals equation expressed as p 5

RT/(y 2 b) 2 a/y

are

M 5 a

y 2 b



 N 5 a

1y 2 b2

c11ThermodynamicRelations.indd Page 640 6/21/10 9:33:59 PM user-s146c11ThermodynamicRelations.indd Page 640 6/21/10 9:33:59 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

11.3 Developing Property Relations

In this section, several important property relations are developed, including the

expressions known as the Maxwell relations. The concept of a fundamental thermo-

dynamic function is also introduced. These results, which are important for subsequent

discussions, are obtained for simple compressible systems of fixed chemical composi-

tion using the concept of an exact differential.

Accordingly, the differential takes the form

dp 5 a

y 2 b

bdT 1 c

2RT

1y 2 b2

ddy

(b) Calculating the mixed second partial derivatives

1y 2 b2

Thus, the mixed second partial derivatives are equal, as expected.

0T2

can be derived using Eqs. 11.15 and 11.16. Thus, with x 5 p, y 5 y, and z 5

T, Eq. 11.16 gives

521

10p

0y2

10T

0p2

Then, with x 5 T, y 5 p, and z 5 y, Eq. 11.15 gives

10p

0T2

Combining these results

10p

0T2

10p

0y2

The numerator and denominator of this expression have been evaluated in part (a), so

➊

1y 2 b2

32RT

1y 2 b2

1 2a

which is the desired result.

➊ Since the van der Waals equation is cubic in specific volume, it can be solved

for y (T, p) at only certain states. Part (c) shows how the partial derivative

10y

0T2

can be evaluated at states where it exists.

Ability to…

❑

use Eqs. 11.15 and 11.16

together with the van der

Waals equation of state to

develop a thermodynamic

property relation.

✓

Skills Developed

Using the results obtained, develop an expression for

of an ideal gas. Ans. y/T.

11.3 Developing Property Relations 641

c11ThermodynamicRelations.indd Page 641 7/25/10 5:15:50 PM user-f391c11ThermodynamicRelations.indd Page 641 7/25/10 5:15:50 PM user-f391 /Users/user-f391/Desktop/Ramakant_25.07.10/Moran_JWCL314/New/Users/user-f391/Desktop/Ramakant_25.07.10/Moran_JWCL314/New

642 Chapter 11

Thermodynamic Relations

11.3.1

Principal Exact Differentials

The principal results of this section are obtained using Eqs. 11.18, 11.19, 11.22, and

11.23. The first two of these equations are derived in Sec. 6.3, where they are

referred to as the T ds equations. For present purposes, it is convenient to express

them as

du 5 T ds 2 p dy (11.18)

dh 5 T ds 1 y dp (11.19)

The other two equations used to obtain the results of this section involve, respec-

tively, the specific

Helmholtz function c defined by

c 5 u 2 Ts (11.20)

and the specific Gibbs function g defined by

g 5 h 2 Ts (11.21)

The Helmholtz and Gibbs functions are properties because each is defined in terms

of properties. From inspection of Eqs. 11.20 and 11.21, the units of c and g are the

same as those of u and h. These two new properties are introduced solely because they

contribute to the present discussion, and no physical significance need be attached to

them at this point.

Forming the differential dc

dc 5 du 2 d1Ts25 du 2 T ds 2 s dT

Substituting Eq. 11.18 into this gives

dc 52p dy 2 s dT (11.22)

Similarly, forming the differential dg

dg 5 dh 2 d1Ts25 dh 2 T ds 2 s dT

Substituting Eq. 11.19 into this gives

dg 5 y dp 2 s dT (11.23)

11.3.2

Property Relations from Exact Differentials

The four differential equations introduced above, Eqs. 11.18, 11.19, 11.22, and 11.23,

provide the basis for several important property relations. Since only properties are

involved, each is an exact differential exhibiting the general form dz 5 M dx 5 N dy

considered in Sec. 11.2. Underlying these exact differentials are, respectively, functions

of the form u(s, y), h(s, p), c(y, T), and g(T, p). Let us consider these functions in the

order given.

The differential of the function u 5 u(s, y) is

du 5 a

ds 1 a

Helmholtz function

Gibbs function

c11ThermodynamicRelations.indd Page 642 6/21/10 9:34:04 PM user-s146c11ThermodynamicRelations.indd Page 642 6/21/10 9:34:04 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New