Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics

Подождите немного. Документ загружается.

Continuing the discussion, when Eq. 11.46 is inserted in Eq. 11.43, the following

expression results.

ds 5

dT 1 a

(11.48)

Inserting Eq. 11.47 into Eq. 11.44 gives

du 5 c

dT 1 cT a

2 p ddy

(11.49)

Observe that the right sides of Eqs. 11.48 and 11.49 are expressed solely in terms of

p, y, T, and c

Changes in specific entropy and internal energy between two states are determined

by integration of Eqs. 11.48 and 11.49, respectively.

2 s

dT 1

(11.50)

2 u

dT 1

cT a

2 p ddy

(11.51)

To integrate the first term on the right of each of these expressions, the variation of

with temperature at one fixed specific volume (isometric) is required. Integration

of the second term requires knowledge of the p–y–T relation at the states of interest.

An equation of state explicit in pressure would be particularly convenient for evalu-

ating the integrals involving 10p

0T2

. The accuracy of the resulting specific entropy

and internal energy changes would depend on the accuracy of this derivative. In cases

where the integrands of Eqs. 11.50 and 11.51 are too complicated to be integrated in

closed form they may be evaluated numerically. Whether closed-form or numerical

integration is used, attention must be given to the path of integration.

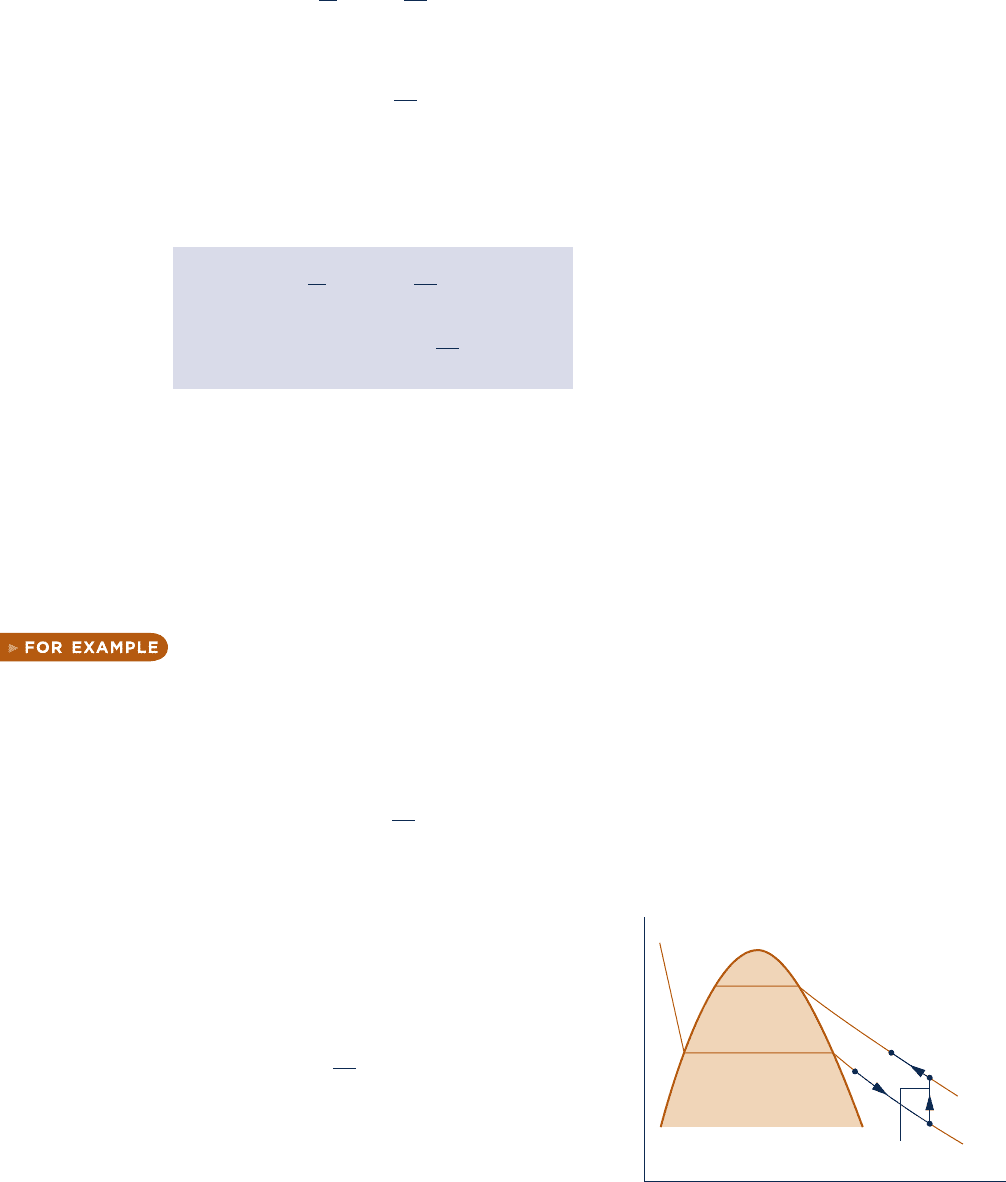
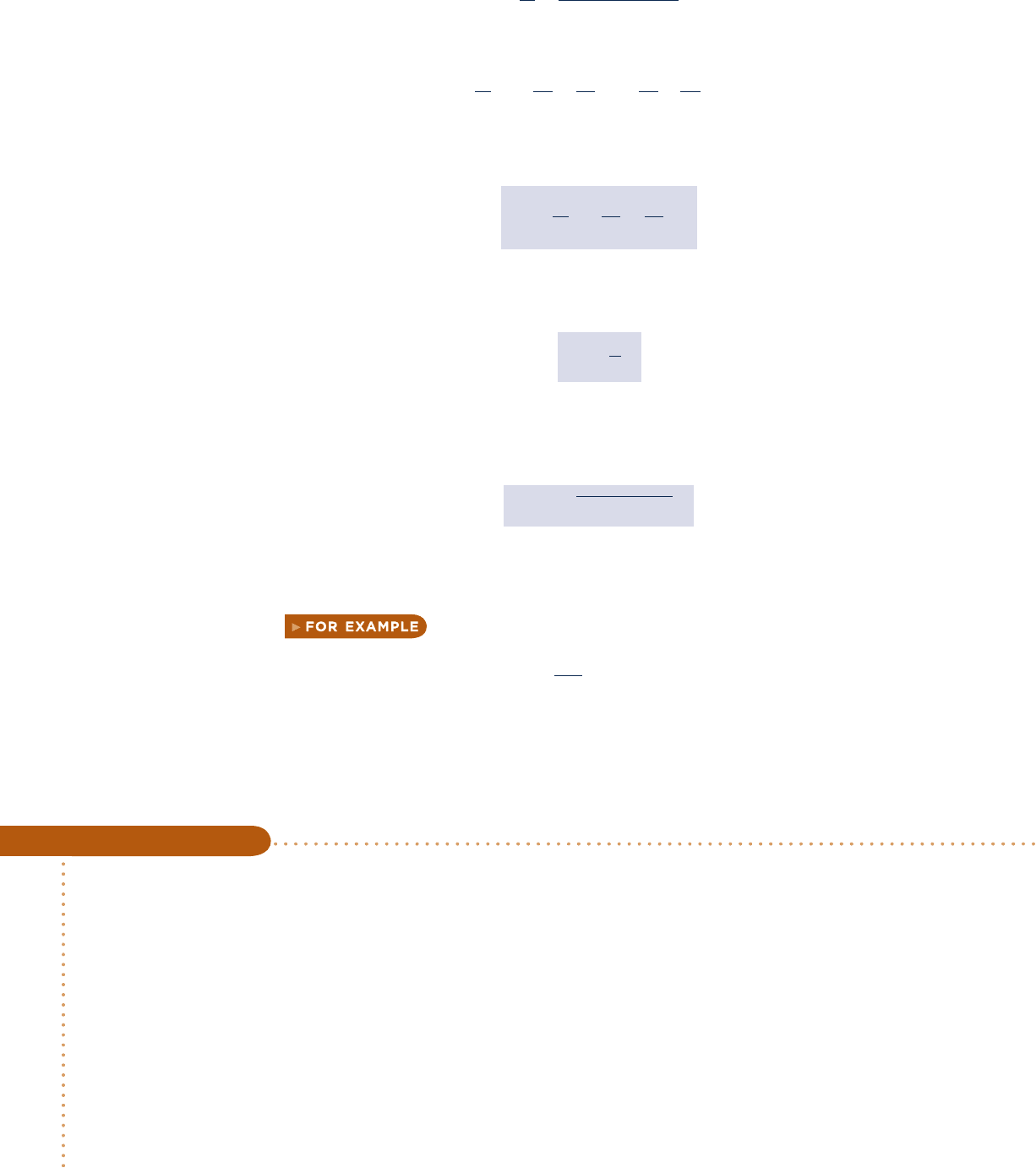
let us consider the evaluation of Eq. 11.51. Referring to Fig. 11.2,

if the specific heat c

is known as a function of temperature along the isometric

(constant specific volume) passing through the states x and y, one possible path of

integration for determining the change in specific internal energy between states 1

and 2 is 1–x–y–2. The integration would be performed in three steps. Since tempera-

ture is constant from state 1 to state x, the first integral of Eq. 11.51 vanishes, so

2 u

cT a

2 p ddy

From state x to y, the specific volume is constant and c

is known as a function of

temperature only, so

2 u

where T

5 T

and T

5 T

. From state y to state 2, the temperature

is constant once again, and

2 u

cT a

2 p ddy

When these are added, the result is the change in specific internal

energy between states 1 and 2.

b b b b b

T AND p AS INDEPENDENT PROPERTIES. In this section a

presentation parallel to that considered above is provided for the

choice of temperature and pressure as the independent properties.

= v

= T

= c

(T, v

)

Fig. 11.2 Integration path between two vapor

states.

11.4 Evaluating Changes in Entropy, Internal Energy, and Enthalpy 653

c11ThermodynamicRelations.indd Page 653 6/21/10 9:34:25 PM user-s146c11ThermodynamicRelations.indd Page 653 6/21/10 9:34:25 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

654 Chapter 11 Thermodynamic Relations

With this choice for the independent properties, the specific entropy can be regarded

as a function of the form s 5 s(T, p). The differential of this function is

ds 5

dT 1

The partial derivative

appearing in this expression can be replaced using the

Maxwell relation, Eq. 11.35, giving

ds 5

dT 2

(11.52)

The specific enthalpy also can be regarded as a function of T and p: h 5 h(T, p).

The differential of this function is

dh 5

dT 1

With c

dh 5 c

dT 1

(11.53)

Substituting Eqs. 11.52 and 11.53 into dh 5 T ds 1 y dp and collecting terms

results in

1 T a

2 y d dp 5 cT a

2 c

d dT

(11.54)

Since pressure and temperature can be varied independently, let us hold pressure

constant and vary temperature. That is, let dp 5 0 and

? 0

. It then follows from

Eq. 11.54 that

(11.55)

Similarly, when dT 5 0 and dp ? 0, Eq. 11.54 gives

5 y 2 T

(11.56)

Equations 11.55 and 11.56, like Eqs. 11.46 and 11.47, are useful thermodynamic prop-

erty relations.

When Eq. 11.55 is inserted in Eq. 11.52, the following equation results:

ds 5

dT 2

(11.57)

Introducing Eq. 11.56 into Eq. 11.53 gives

dh 5 c

dT 1 cy 2 T a

(11.58)

Observe that the right sides of Eqs. 11.57 and 11.58 are expressed solely in terms of

p, y, T, and c

Changes in specific entropy and enthalpy between two states are found by integrat-

ing Eqs. 11.57 and 11.58, respectively

2 s

dT 2

(11.59)

c11ThermodynamicRelations.indd Page 654 6/21/10 9:34:29 PM user-s146c11ThermodynamicRelations.indd Page 654 6/21/10 9:34:29 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

2 h

dT 1

cy 2 T a

d dp

(11.60)

To integrate the first term on the right of each of these expressions, the variation of

with temperature at one fixed pressure (isobar) is required. Integration of the

second term requires knowledge of the p–y–T behavior at the states of interest. An

equation of state explicit in y would be particularly convenient for evaluating the

integrals involving 10y

0T2

. The accuracy of the resulting specific entropy and enthalpy

changes would depend on the accuracy of this derivative.

Changes in specific enthalpy and internal energy are related through h 5 u 1 py by

2 h

2 u

2 p

(11.61)

Hence, only one of Dh and Du need be found by integration. Then, the other can be

evaluated from Eq. 11.61. Which of the two property changes is found by integration

depends on the information available. Dh would be found using Eq. 11.60 when an

equation of state explicit in y and c

as a function of temperature at some fixed pres-

sure are known. Du would be found from Eq. 11.51 when an equation of state explicit

in p and c

as a function of temperature at some specific volume are known. Such

issues are considered in Example 11.5.

11.4 Evaluating Changes in Entropy, Internal Energy, and Enthalpy 655

Evaluating Ds, Du, and Dh of a Gas

c c c c EXAMPLE 11.5 c

Using the Redlich–Kwong equation of state, develop expressions for the changes in specific entropy, internal

energy, and enthalpy of a gas between two states where the temperature is the same, T

5 T

, and the pressures

are p

and p

, respectively.

SOLUTION

Known:

Two states of a unit mass of a gas as the system are fixed by p

and T

at state 1 and p

, T

(5 T

) at

state 2.

Find: Determine the changes in specific entropy, internal energy, and enthalpy between these two states.

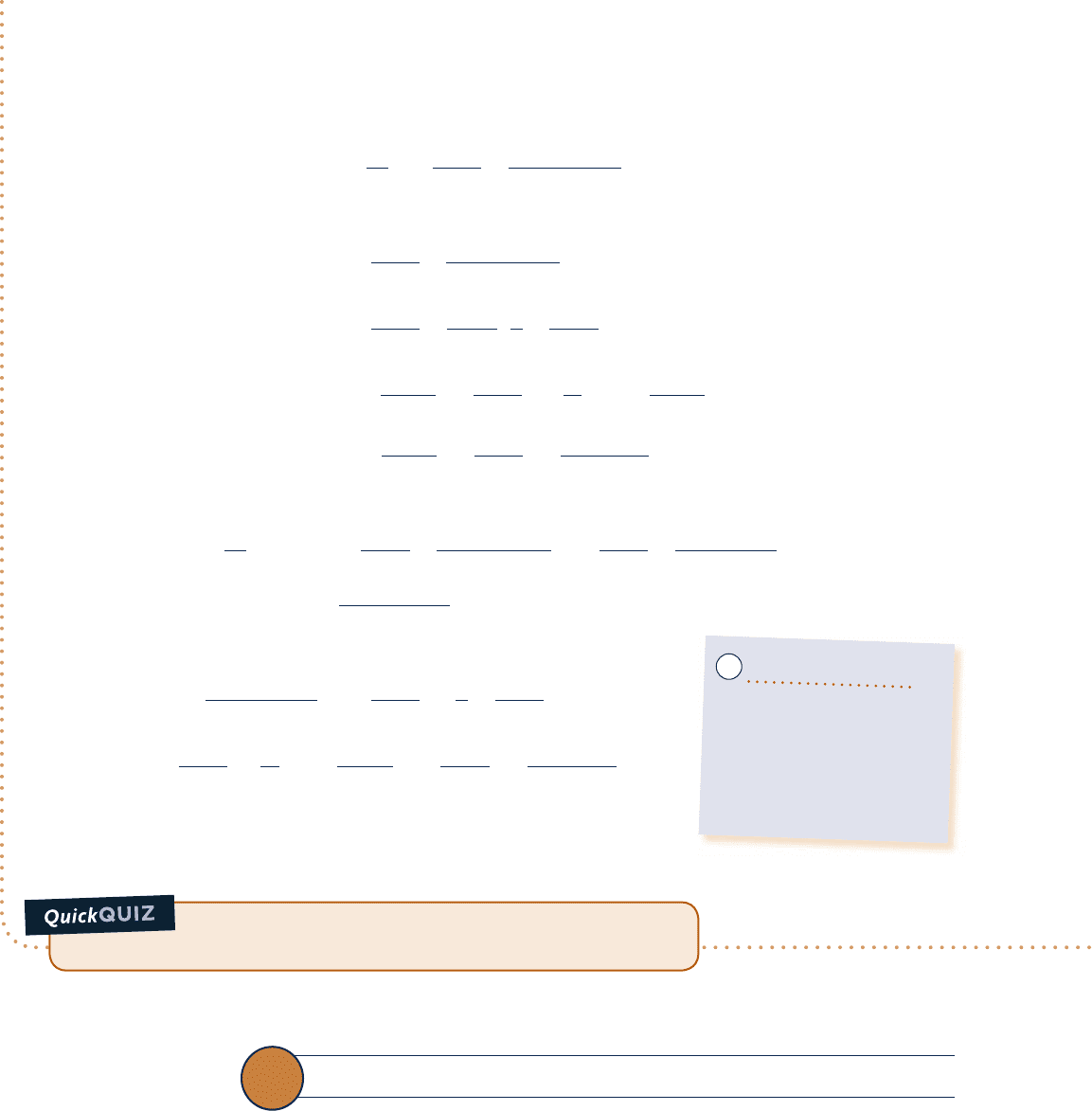
Schematic and Given Data:

Engineering Model:

The Redlich–Kwong equation of state represents the

p–y–T behavior at these states and yields accurate values for

Analysis: The Redlich–Kwong equation of state is explicit in pressure, so Eqs. 11.50 and 11.51 are selected for

determining s

2 s

and u

2 u

. Since T

5 T

, an isothermal path of integration between the two states is

convenient. Thus, these equations reduce to give

2 s

2 u

cT a

2 p ddy

Isotherm

Fig. E11.5

c11ThermodynamicRelations.indd Page 655 6/21/10 9:34:30 PM user-s146c11ThermodynamicRelations.indd Page 655 6/21/10 9:34:30 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

656 Chapter 11 Thermodynamic Relations

The limits for each of the foregoing integrals are the specific volumes y

and y

at the two states under con-

sideration. Using p

, p

, and the known temperature, these specific volumes would be determined from the

Redlich–Kwong equation of state. Since this equation is not explicit in specific volume, the use of an equation

solver such as Interactive Thermodynamics: IT is recommended.

The above integrals involve the partial derivative

, which can be determined from the Redlich–Kwong

equation of state as

y 2 b

2y1y 1 b2T

Inserting this into the expression for (s

2 s

) gives

2 s

y 2 b

2y1y 1 b2T

d dy

y 2 b

2bT

y 1 b

bd dy

5 R ln a

2 b

2bT

cln a

b2 ln a

1 b

5 R ln a

2 b

2bT

ln c

1 b2

1 b

With the Redlich–Kwong equation, the integrand of the expression for (u

2 u

) becomes

cT a

2 p d5 T c

y 2 b

y 1 b

d2 c

y 2 b

y 1 b

2y1y

b2T

Accordingly

2 u

2y1y 1 b2T

dy 5

2bT

y 1 b

2bT

cln

2 ln a

1 b

bd5

2bT

ln c

1 b2

1 b

Finally, (h

2 h

) would be determined using Eq. 11.61 together with the

known values of (u

2 u

), p

, y

, p

, and y

Using results obtained, develop expressions for Du and Ds of

an ideal gas. Ans. Du 5 0, Ds 5 R ln (y

11.5 Other Thermodynamic Relations

The presentation to this point has been directed mainly at developing thermody-

namic relations that allow changes in u, h, and s to be evaluated from measured

property data. The objective of the present section is to introduce several other

thermodynamic relations that are useful for thermodynamic analysis. Each of the

properties considered has a common attribute: it is defined in terms of a partial

derivative of some other property. The specific heats c

and c

are examples of this

type of property.

Ability to…

❑

perform differentiations and

integrations required to

evaluate Du and Ds using

the two-constant Redlich–

Kwong equation of state.

✓

Skills Developed

c11ThermodynamicRelations.indd Page 656 6/21/10 9:34:34 PM user-s146c11ThermodynamicRelations.indd Page 656 6/21/10 9:34:34 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

11.5.1

Volume Expansivity, Isothermal and Isentropic

Compressibility

In single-phase regions, pressure and temperature are independent, and we can think

of the specific volume as being a function of these two, y 5 y(T, p). The differential

of such a function is

dy 5

dT 1

Two thermodynamic properties related to the partial derivatives appearing in this dif-

ferential are the volume expansivity b, also called the coefficient of volume expansion

b 5

(11.62)

and the isothermal compressibility k

k 52

(11.63)

By inspection, the unit for b is seen to be the reciprocal of that for temperature and

the unit for k is the reciprocal of that for pressure. The volume expansivity is an

indication of the change in volume that occurs when temperature changes while pres-

sure remains constant. The isothermal compressibility is an indication of the change

in volume that takes place when pressure changes while temperature remains con-

stant. The value of k is positive for all substances in all phases.

The volume expansivity and isothermal compressibility are thermodynamic prop-

erties, and like specific volume are functions of T and p. Values for b and k are

provided in compilations of engineering data. Table 11.2 gives values of these prop-

erties for liquid water at a pressure of 1 atm versus temperature. For a pressure of

1 atm, water has a state of maximum density at about 48C. At this state, the value of

b is zero.

The isentropic compressibility a is an indication of the change in volume that occurs

when pressure changes while entropy remains constant:

a 52

(11.64)

The unit for a is the reciprocal of that for pressure.

11.5 Other Thermodynamic Relations 657

isothermal compressibility

volume expansivity

isentropic compressibility

Volume Expansivity B and Isothermal Compressibility

K of Liquid Water at 1 atm Versus Temperature

T Density b 3 10

k 3 10

( 8C) (kg/m

) (K)

(bar)

0 999.84 268.14 50.89

10 999.70 87.90 47.81

20 998.21 206.6 45.90

30 995.65 303.1 44.77

40 992.22 385.4 44.24

50 988.04 457.8 44.18

TABLE 11.2

c11ThermodynamicRelations.indd Page 657 6/21/10 9:34:36 PM user-s146c11ThermodynamicRelations.indd Page 657 6/21/10 9:34:36 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

658 Chapter 11

Thermodynamic Relations

The isentropic compressibility is related to the speed at which sound travels in a

substance, and such speed measurements can be used to determine a. In Sec. 9.12.2,

the velocity of sound, or sonic velocity, is introduced as

c 5

(9.36b)

The relationship of the isentropic compressibility and the velocity of sound can be

obtained using the relation between partial derivatives expressed by Eq. 11.15. Iden-

tifying p with x, y with y, and s with z, we have

10y

0p2

With this, the previous two equations can be combined to give

c 5 1y

a (11.65)

The details are left as an exercise.

TAKE NOTE...

Through the Mach number,

the sonic velocity c plays

an important role in analyz-

ing flow in nozzles and

diffusers. See Sec. 9.13.

velocity of sound

BIOCONNECTIONS The propagation of elastic waves, such as sound waves,

has important implications related to injury in living things. During impact such as

a collision in a sporting event (see accompanying figure), elastic waves are created

that cause some bodily material to move relative to the rest of the body. The waves can

propagate at supersonic, transonic, or subsonic speeds depending on the nature of the

impact, and the resulting trauma can cause serious damage. The waves may be focused

into a small area, causing localized damage, or they may be reflected at the boundary of

organs and cause more widespread damage.

An example of the focusing of waves occurs in some head injuries. An impact to the

skull causes flexural and compression waves to move along the curved surface and arrive

at the far side of the skull simultaneously. Waves also propagate through the softer brain

tissue. Consequently, concussions, skull fractures, and other injuries can appear at loca-

tions away from the site of the original impact.

Central to an understanding of traumatic injury is data on speed of sound and other

elastic characteristics of organs and tissues. For humans the speed of sound varies widely,

from approximately 30–45 m/s in spongy lung tissue to about 1600 m/s in muscle and

3500 m/s in bone. Because the speed of sound in the lungs is relatively low, impacts such

as in automobile collisions or even air-bag deployment can set up waves that propagate super-

sonically. Medical personnel responding to traumas are trained to check for lung injuries.

The study of wave phenomena in the body constitutes an important area in the field of

biomechanics.

11.5.2

Relations Involving Specific Heats

In this section, general relations are obtained for the difference between specific heats

2 c

) and the ratio of specific heats c

EVALUATING (c

2 c

). An expression for the difference between c

and c

can be obtained by equating the two differentials for entropy given by Eqs. 11.48

and 11.57 and rearranging to obtain

2 c

dT 5 T a

dy 1 T a

c11ThermodynamicRelations.indd Page 658 7/23/10 6:24:21 PM user-s146c11ThermodynamicRelations.indd Page 658 7/23/10 6:24:21 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

Considering the equation of state p 5 p(T, y), the differential dp can be expressed as

dp 5

dT 1

Eliminating dp between the last two equations and collecting terms gives

c1c

2 c

22 T a

d dT 5 T ca

1 a

d dy

Since temperature and specific volume can be varied independently, the coefficients

of the differentials in this expression must vanish, so

2 c

5 T

(11.66)

(11.67)

Introducing Eq. 11.67 into Eq. 11.66 gives

2 c

52T a

(11.68)

This equation allows c

to be calculated from observed values of c

knowing only

p–y–T data, or c

to be calculated from observed values of c

for the special case of an ideal gas, Eq. 11.68 reduces to Eq. 3.44:

5 c

1 R, as can readily be shown. b b b b b

The right side of Eq. 11.68 can be expressed in terms of the volume expansivity b

and the isothermal compressibility k. Introducing Eqs. 11.62 and 11.63, we get

2 c

5 y

(11.69)

In developing this result, the relationship between partial derivatives expressed by

Eq. 11.15 has been used.

Several important conclusions about the specific heats c

and c

can be drawn from

Eq. 11.69.

since the factor b

cannot be negative and k is positive for all

substances in all phases, the value of c

is always greater than, or equal to, c

. The

specific heats are equal when b 5 0, as occurs in the case of water at 1 atmosphere

and 48C, where water is at its state of maximum density. The two specific heats also

become equal as the temperature approaches absolute zero. For some liquids and

solids at certain states, c

and c

differ only slightly. For this reason, tables often give

the specific heat of a liquid or solid without specifying whether it is c

or c

. The data

reported are normally c

values, since these are more easily determined for liquids

and solids. b b b b b

EVALUATING c

. Next, let us obtain expressions for the ratio of specific

heats, k. Employing Eq. 11.16, we can rewrite Eqs. 11.46 and 11.55, respectively, as

10p

0s2

10T

0p2

11.5 Other Thermodynamic Relations 659

c11ThermodynamicRelations.indd Page 659 6/21/10 9:34:42 PM user-s146c11ThermodynamicRelations.indd Page 659 6/21/10 9:34:42 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

660 Chapter 11 Thermodynamic Relations

Forming the ratio of these equations gives

(11.70)

Since

5 1

and

5 1

, Eq. 11.70 can be expressed as

5 ca

dca

(11.71)

Finally, the chain rule from calculus allows us to write

and

10p

0y2

5 10p

0T2

10T

0y2

, so Eq. 11.71 becomes

k 5

(11.72)

This can be expressed alternatively in terms of the isothermal and isentropic com-

pressibilities as

k 5

(11.73)

Solving Eq. 11.72 for 10p

0y2

and substituting the resulting expression into Eq. 9.36b

gives the following relationship involving the velocity of sound c and the specific heat

ratio k

c 5 22ky

10p

0y2

(11.74)

Equation 11.74 can be used to determine c knowing the specific heat ratio and p–y–T

data, or to evaluate k knowing c and 10p

0y2

in the special case of an ideal gas, Eq. 11.74 reduces to give

Eq. 9.37 (Sec. 9.12.2):

c 5 1kRT



1ideal gas2 (9.37)

as can easily be verified. b b b b b

In the next example we illustrate the use of specific heat relations introduced above.

Using Specific Heat Relations

c c c c EXAMPLE 11.6 c

For liquid water at 1 atm and 208C, estimate (a) the percent error in c

that would result if it were assumed that

5 c

, (b) the velocity of sound, in m/s.

SOLUTION

Known:

The system consists of a fixed amount of liquid water at 1 atm and 208C.

Find: Estimate the percent error in c

that would result if c

were approximated by c

, and the velocity of sound,

in m/s.

c11ThermodynamicRelations.indd Page 660 6/21/10 9:34:43 PM user-s146c11ThermodynamicRelations.indd Page 660 6/21/10 9:34:43 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

➋

Analysis:

(a)

Equation 11.69 gives the difference between c

and c

. Table 11.2 provides the required values for the

volume expansivity b, the isothermal compressibility k, and the specific volume. Thus

2 c

5 y

5 a

998.21 kg

b1293 K2a

206.6 3 10

bar

45.90 3 10

5 a272.96 3 10

bar ? m

kg ? K

1 bar

1 kJ

N ? m

5 0.027

kg ? K

➊ Interpolating in Table A-19 at 208C gives c

5 4.188 kJ/kg ? K Thus, the value of c

5 4.188 2 0.027 5 4.161



kg ? K

Using these values, the percent error in approximating c

by c

2 c

b110025 a

0.027

4.161

b110025 0.6%

(b) The velocity of sound at this state can be determined using Eq. 11.65. The required value for the isentropic

compressibility a is calculable in terms of the specific heat ratio k and the isothermal compressibility k. With

Eq. 11.73, a 5 k/k. Inserting this into Eq. 11.65 results in the following expression for the velocity of sound

c 5

The values of y and k required by this expression are the same as used in part (a). Also, with the values of

and c

from part (a), the specific heat ratio is k 5 1.006. Accordingly

c 5

11.0062110

2 bar

1998.21 kg

2145.902

1 bar

1 kg ? m

1 N

`5 1482 m

➊ Consistent with the discussion of Sec. 3.10.1, we take c

at 1 atm and 208C as

the saturated liquid value at 208C.

➋ The result of part (a) shows that for liquid water at the given state, c

and

are closely equal.

❸ For comparison, the velocity of sound in air at 1 atm, 208C is about

343 m/s, which can be checked using Eq. 9.37.

Ability to…

❑

apply specific heat relations

to liquid water.

❑

evaluate velocity of sound

for liquid water.

✓

Skills Developed

A submarine moves at a speed of 20 knots (1 knot 5

1.852 km/h). Using the sonic velocity calculated in part (b), estimate the

Mach number of the vessel relative to the water.

Ans. 0.0069.

11.5.3

Joule–Thomson Coefficient

The value of the specific heat c

can be determined from p–y–T data and the Joule–

Thomson coefficient. The Joule–Thomson coefficient m

is defined as

5 a

(11.75)

Joule–Thomson

coefficient

11.5 Other Thermodynamic Relations 661

❸

c11ThermodynamicRelations.indd Page 661 6/21/10 9:34:44 PM user-s146c11ThermodynamicRelations.indd Page 661 6/21/10 9:34:44 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

662 Chapter 11

Thermodynamic Relations

Like other partial differential coefficients introduced in this section, the Joule–

Thomson coefficient is defined in terms of thermodynamic properties only and thus

is itself a property. The units of m

are those of temperature divided by pressure.

A relationship between the specific heat c

and the Joule–Thomson coefficient m

can be established by using Eq. 11.16 to write

521

The first factor in this expression is the Joule–Thomson coefficient and the third is

. Thus

10p

0h2

With 10h

0p2

5 1

10p

0h2

from Eq. 11.15, this can be written as

(11.76)

The partial derivative

, called the constant-temperature coefficient, can be

eliminated from Eq. 11.76 by use of Eq. 11.56. The following expression results:

cT a

2 y d

(11.77)

Equation 11.77 allows the value of c

at a state to be determined using p–y–T data

and the value of the Joule–Thomson coefficient at that state. Let us consider next

how the Joule–Thomson coefficient can be found experimentally.

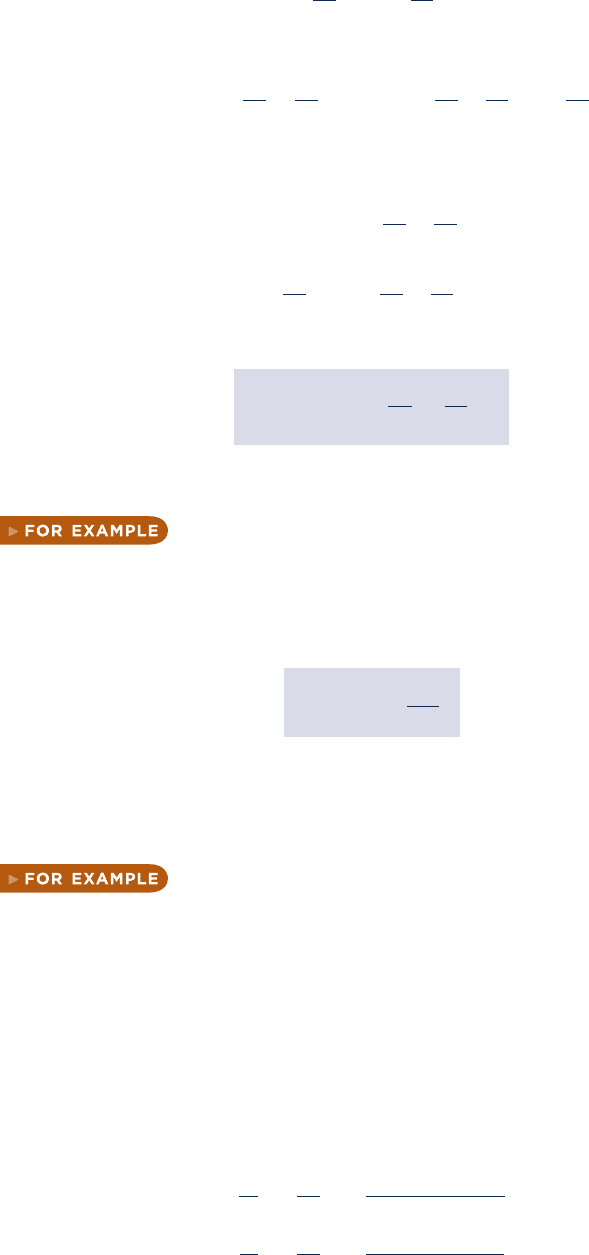
EXPERIMENTAL EVALUATION. The Joule–Thomson coefficient can be evalu-

ated experimentally using an apparatus like that pictured in Fig. 11.3. Consider first

Fig. 11.3a, which shows a porous plug through which a gas (or liquid) may pass. During

operation at steady state, the gas enters the apparatus at a specified temperature T

and pressure p

and expands through the plug to a lower pressure p

, which is controlled

by an outlet valve. The temperature T

at the exit is measured. The apparatus is designed

Inversion state

Inversion

state

Inversion

state

Critical

point

Triple

point

Vapor

Inlet state

, p

)

∂T

––

∂p

(

)

Liquid

Solid

(b)(a)

Inlet

, p

Porous plug

, p

Valve

Fig. 11.3 Joule–Thomson expansion. (a) Apparatus. (b) Isenthalpics on a T–p diagram.

c11ThermodynamicRelations.indd Page 662 6/21/10 9:34:47 PM user-s146c11ThermodynamicRelations.indd Page 662 6/21/10 9:34:47 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New