Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple
Подождите немного. Документ загружается.

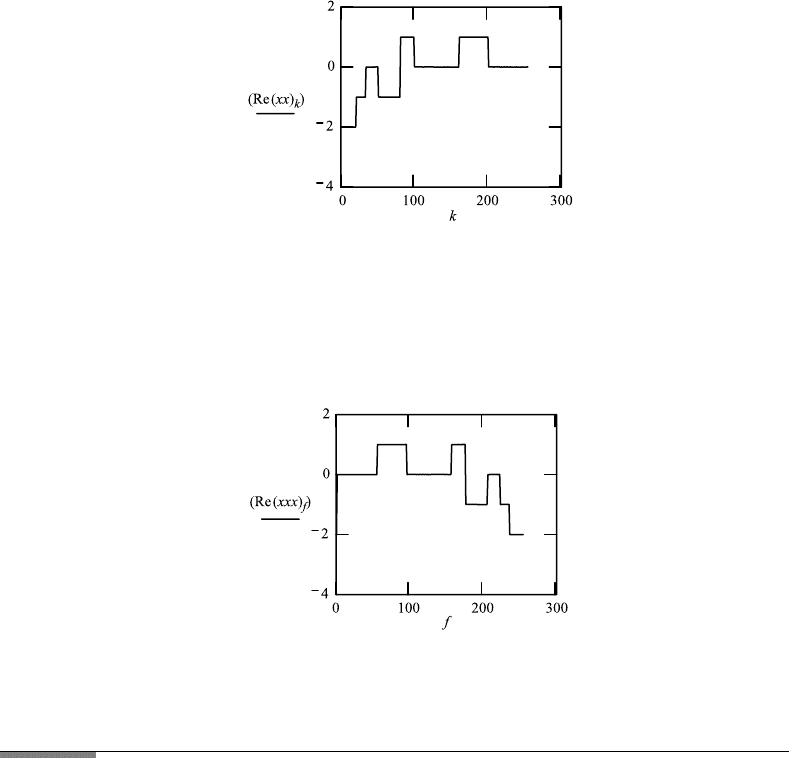
382 10. IMAGING USING WAVE THEORY
The inverse Fourier transformation
xx : icfft(cc) Nxx : last(xx)
Nxx 255 k : 0 ...Nxx − 1.
3. Application of cfft the second time, instead of the inverse icfft results in an
image with the left-right interchanged.
xxx : cf f t (cc)
Nxxx : last(xxx) Nxxx 255
f : 0 ...Nxxx − 1.
10.3 OBJECT, IMAGE, AND THE TWO FOURIER
TRANSFORMATIONS
10.3.1 Waves from Object and Aperture Plane and Lens
In geometrical optics, we employed the thin lens equation to find the image point
x
i
of an object point x
0
, when using a thin lens of focal length f . The image
of an extended object was obtained by imaging each point of the object to its
conjugate point at the image.
The application of wave theory to the image forming process is also done in
a point-by-point procedure. The image points are in the y, z plane, and at the
distance x a lens is positioned; the finite aperture of the lens is described in the

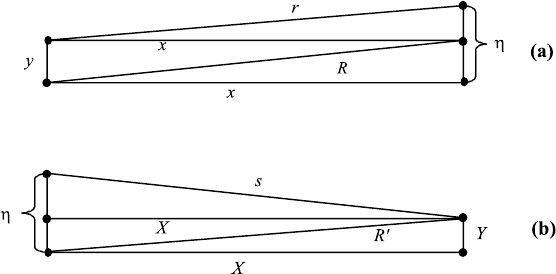
10.3. OBJECT, IMAGE, AND THE TWO FOURIER TRANSFORMATIONS 383
FIGURE 10.3 Coordinate system for object plane, aperture plane, and image plane.
η, ζ plane. At distance X from the lens is the image plane and the image is
described in that plane by Y , Z coordinates (see Figure 10.3).
1
We assume monochromatic light and consider two summation processes and
the action of the lens. The action of the lens was discussed in Chapter 3 for the
case of Fraunhofer observation. The aperture of the lens is described by α(η, ζ ),
and the changes of the incident wavefront to the wavefront leaving the lens is
given by exp(−ik(η
2
+ζ
2
)/2f ). The lens bends the wavefront in such a way that
it converges to the focal point. The phase factor may be written as e
ikρ
where ρ is
in the direction of propagation. We obtain ρ η
2
/2f and as a result e
ikρ
is equal
to exp(ikη
2
/2f ). For simplicity, without losing essential points of importance,
we restrict our discussions to a one-dimensional extension of object, lens, and
image.
10.3.2 Summation Processes
10.3.2.1 The First Summation Process
The magnitude of the object points is described by h(y, z) and from each point a
spherical wave emerges, described by h(y, z)e
ikr
/r. All the waves are summed
up for each point η, ζ in the plane of the lens. In the following we restrict the
considerations to one dimension.
We call h(y) the magnitude of each object point and calculate r in e
ikr
/r in
terms of x, y, and η (see Figure 10.4)
r
2
(η − y)
2
+ x
2
η
2
− 2ηy + y
2
+ x
2
R
2
+ η
2
− 2ηy (10.2)
R
2
(1 + (η
2
− 2ηy)/R
2
),
where we call y
2
+ x
2
R
2
and we consider R
2
as a constant because y x.
Developing the square root of [R
2
(1 + (η
2
− 2ηy)/R
2
)] yields
r ≈ R{1 + (η
2
− 2ηy)/2R
2
}≈R − ηy/R + η
2
/2R. (10.3)
1
See Physical Optics Notebook by G. P. Parrent and B. J. Thompson, Society of Photo-Optical Engineers,
Redondo Beach, California, 1969.
384 10. IMAGING USING WAVE THEORY
FIGURE 10.4 Coordinates for small angle approximation.
For the first summation process we integrate over all y and have
h(y)exp{ik(R − ηy/R + η
2
/2R)}dy. (10.4)
10.3.2.2 Action Lens
The aperture is presented by α(η) and from the chapter on diffraction we know
that the wavefront is changed by a phase factor of exp(−ikη
2
/2f ).
10.3.2.3 Second Summation Process
From each point in the plane η, ζ emerges a spherical wave α(η, ζ)e
iks
/s. These
amplitudes, including the phase factor introduced by the lens, are summed up
for all final image points X, Y .
In a similar way as discussed in Section 10.3.2.1 we may write approximately
(Figure 10.4) s ≈ R
− ηY/R
+ η
2
/2R
, with R
2
X
2
+ Y
2
considered as
a constant. The amplitude at the image point is called g(Y ) for both summation
processes
g(Y )
h(y)(1/R){exp ik(R − ηy/R +η
2
/2R)}dy
α(η)
{exp(−ikη
2
/2f )(1/R
)}
{exp ik(R
− ηY/R
+ η
2
/2R
)}dη, (10.5)
where one has approximately 1/R for 1/r and 1/R
for 1/s. All the constants
are taken before the integral and one gets
g(Y ) (1/RR
)expik(R + R
)
h(y)exp{−ikηy/R}dy
α(η){exp ik(η
2
/2R − η
2
/2f + η
2
/2R
)}exp ik(−ηY/R
)dη. (10.6)
Since we are treating an imaging process, we introduce R ≈ x
0
and R
≈ x
i
into
exp{ik η
2
/2R − η
2
/2f + η
2
/R
)}, and make the factor 1 by using the thin
10.3. OBJECT, IMAGE, AND THE TWO FOURIER TRANSFORMATIONS 385
lens equation
(ikη
2
/2)(1/x
0
− 1/f + 1/x
i
) 0. (10.7)
Calling the factor before the integral C, we have further to consider
g(Y ) C
h(y)exp{−ikηy/x
0
}dy
α(η)exp{−ikηY/x
i
}dη. (10.8)
10.3.3 The Pair of Fourier Transformations
10.3.3.1 Aperture Function α(η) of the Lens Is a Constant
When α(η) is independent of η we can include it in the constant before the
integral and have
g(Y ) C
h(y)exp{−ikηy/x
0
}dy
exp{−ikηY/x
i
}dη. (10.9)
The integrationovery produces a function of η and we call the integral in brackets
ω(η)
ω(η)
h(y)exp{−ikηy/x
0
}dy (10.10)
and write
g(Y ) C
ω(η)exp{−ikηY/x
i
}dη. (10.11)
The result is: The image amplitude function g(Y ) is the Fourier transform of
the Fourier transform of the object amplitude function h(y).
Since the Fourier transform of the Fourier transform is the original function,
except for a scaling factor, for this idealized case the result is that the function
representing the image is the same as the function representing the object, except
for a scaling factor and phase factor.
10.3.3.2 Aperture Function α(η) of the Lens Is Not a Constant
When α(η) is not a constant, we may write, using ω(η),
g(Y ) C
ω(η)α(η)exp{−ikηY/x
i
}dη. (10.12)
We have as the result: The Fourier transform of the modified Fourier transform
of the object function is the image function. The function α(η) is in most cases
an aperture function such as a step function or in two dimensions a function
representing a round hole. In that case only the magnitude in the η direction
(in two dimensions, the η, ζ plane) is altered. However, α(η) may also contain
a phase factor representing phase differences between certain points (η)inthe
plane (η, ζ ).

386 10. IMAGING USING WAVE THEORY
10.4 IMAGE FORMATION USING INCOHERENT
LIGHT
10.4.1 Spread Function
We have assumed in the preceding chapters that monochromatic light was used
for image formation. We now want to use nonmonochromatic light, (e.g., light
from the sun) for image formation. To do this we will assume that there is
no fixed phase relation between the light emitted from a pair of object points.
Since we want to use only one medium wavelength, the light we assume using
is called quasimonochromatic light (see Chapter 4). The case where one uses
monochromatic light is discussed in Section 10.5. As in geometrical optics, we
consider the object made of points and apply a point-by-point process to obtain
the image. The detector used for recording the image will be sensitive to the
intensity at each image point, which we assume to be proportional to the square
of the amplitude.
When considering one point, we have to replace h(y) (see Section 10.4.2) by
a delta function and have from Eq. (10.8),
s(Y ) C
[
δ(y)exp{−ikηy/x
0
}dy]α(η)exp{−ikηY/x
i
}dη. (10.13)
Since
δ(y)exp{−ikηy/x
0
}dy 1 (10.14)
we get
s(Y ) C
α(η)exp{−ikηY/x
i
}dη. (10.15)
If α(η) is a constant and s(Y ) is a delta function equal to the object function h(y)
we have a point-to-point imaging process. In general, if α(η) is not a constant we
go back to the first summation process and find for the two-dimensional process
that α(η, ζ ) describes the amplitude distribution of the light from the point source
in the plane of the lens. Therefore s(Y ) describes the deviation from a point we
would have obtained as the image point.
For the image one needs the intensity and has to square Eq. (10.15) and obtain
S(Y ) |C
α(η)exp{−ikηY/x
i
}dη|
2
. (10.16)
We call S(Y ) the spread function. This is the spread of the object point in the
image plane as produced by the lens.
10.4. IMAGE FORMATION USING INCOHERENT LIGHT 387
10.4.2 The Convolution Integral
The integral in Eq. eq10.15 may be rewritten using the convolution theorem of
Fouriertransformations.This theorem tells us that we may write the Fourier trans-
form of a product of two functions, here ω(η)α(η), as the convolution integral
of the Fourier transformation of ω(η) and of α(η).
We consider the integral in Eq. (10.12),
g(Y ) C
ω(η)α(η)exp{−ikηY/x
i
}dη. (10.17)
From Eq. (10.10) we have
ω(η)
h(y)exp{−ikηy/x
0
}dy. (10.18)
The Fourier transform is the original object function
h(Y ) C
ω(η)exp{−ikηY/x
i
}dη. (10.19)
From Eq. (10.15) we have
s(Y ) C
α(η)exp{−ikηY/x
i
}dη (10.20)
and may replace g(Y ) in Eq. (10.17) by the convolution integral
g(Y ) C
h(Y )s(τ − Y )dτ. (10.21)
The effect of the aperture function α(η) is that the final image function is obtained
by convolving the original object function h(Y ) with the Fourier transform of
the aperture function α(η), which is s(Y ) (using image coordinates).
The result is that only the coordinates of the image plane are involved.
10.4.3 Impulse Response and the Intensity Pattern
If the object is described by I
ob
(Y ), a point of the object on the object screen can
be represented by the product I
ob
(Y ) times a δ function
I
ob
(Y )δ(Y − Y
), (10.22)
which will have the value I
ob
(Y
) for Y Y
.
For a very large aperture, nothing would happen to the δ function and we
would have on the observation screen a point. The image point is similar to the
object point but we may have to introduce a scaling factor. For a small aperture,
the point would spread to a certain pattern and we would have to replace δ(Y −Y
)
by the spread function S(Y − Y
). The spread function describes the change of
the object as it appears on the observation screen. The distortion is produced by
388 10. IMAGING USING WAVE THEORY
the lens.
I
ob
(Y )δ(Y − Y
) −→ I
ob
(Y )S(Y − Y
). (10.23)
If the object is only one point we call this the impulse response. For incoherent
light, the spread function is the image of one point on the object screen. If a
second point is added on the object screen, it has to be treated similarly and
independently and the result has to be added to the image plane. For n points we
have for the impulse response
I
im
(Y )
I
ob
(Y
n
)S(Y − Y
n
) (10.24)
and for a continuous distribution of points we obtain
I
im
(Y )
I
ob
(Y
)S(Y − Y
)dY
. (10.25)
With Eq. (10.25) one is able to calculate the image from an object when the
spread function is known. This is demonstrated in the following for a few simple
examples.
10.4.4 Examples of Convolution with Spread Function
10.4.4.1 One Bar as an Object and Application of a Cylindrical Lens
We assume that the object is made of just one bar, represented by h(y)asa
rectangular pulse of height 1 and width from y b1toy b2. The lens is a
cylindrical lens represented as a pulse by the function α(η) of height 1 and width
from η −a to η +a (see FileFig 10.3). We call the focal length of the lens
f and its diameter 2a. One calls f/2a the f # of the lens.
The spread, which is produced by the lens, is presented by the spread function
S(Y ) (Eq. (10.16)) where we have set X f , with f being the focal length of
the lens
S(Y ) |
{e
−ikYη/f
}dη|
2
. (10.26)
For a cylindrical lens we have to integrate over −a to a and get
S(Y ) 4a
2
{(sin kaY/f )/(kaY/f )}
2
. (10.27)
The image is then obtained from the convolution integral
I
im
(Y ) 4a
2
Y
b2
Y
b1
I
ob
(Y
)S(Y − Y
)dY
, (10.28)
where we used Y
YY in FileFig 10.3. There we show the object and image,
with γ 0.0005 mm, diameter of the lens 2a, and choice of f # 10. The width
of the object bar has been assumed to be from b1 −0.002 to b2 0.002.
10.4. IMAGE FORMATION USING INCOHERENT LIGHT 389
FileFig 10.3 (W3IMONES)
The object is one bar. The image is obtained by convolution of the object function
with the spread function. The spread function is the Fourier transformation of
the pulse, representing the cylindrical lens.
W3IMONEBS is only on the CD.
Application 10.3.
1. Change the values of b1, b2, and a so that b2 −b1 is larger than a.
2. Change the values of b1, b2, and a so that b2 −b1 is smaller than a.
10.4.4.2 Two Bars
Two bars are considered in FileFig 10.4, each of width 0.003, and center-to-center
distance of bb 0.013. The lens has width 2a, and we use for the wavelength
λ 0.0005 mm and for the f # 10. The image of each bar is calculated
separately with the integral of Eq. (10.28). Because of the linearity of the system
the final image is the superposition of the result of imaging of each bar separately.
FileFig 10.4 (W4IMTWOB)
The object is made of two bars. The image is obtained by convolution of each
object function with the spread function. The spread function is the Fourier
transformation of the pulse, representing the cylindrical lens.
W4IMTWOB is only on the CD.
Application 10.4.
1. Change the distance between the two object bars and study the resolution. If
the distance is too small, the image is just one peak.
2. Change the calculation and apply the spread function to the total image over
a large range of integration. The image is now more similar to the object.
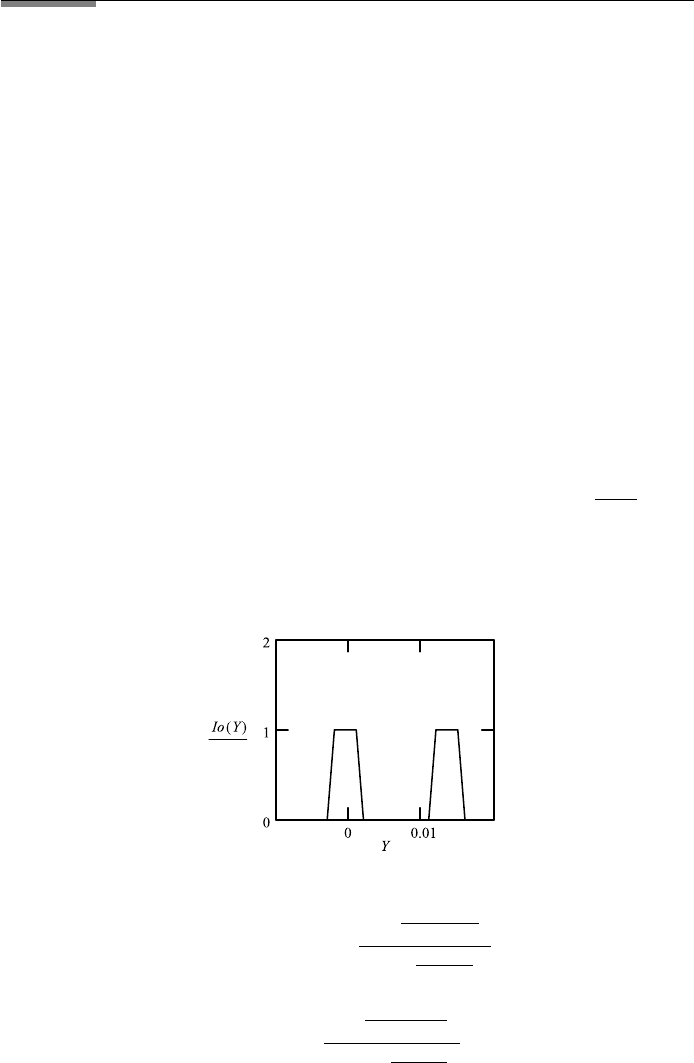
10.4.4.3 One Round Object and a Circular Lens
In far field diffraction of the round aperture, one finds that the two-dimensional
problem is reduced to a one-dimensional circular symmetric problem, solved by
using the Bessel function. We may similarly proceed for imaging. The object
is a round aperture of diameter 2b 0.004 (FileFig 10.5). The round lens
has the diameter 2a. For the calculation of the integral, corresponding to the
integral of Eq. (10.28), we extend the definition of the radius as it appears in the

390 10. IMAGING USING WAVE THEORY
Bessel function to negative values. The spread function is calculated using the
nonnormalized Bessel function
s
2
(R) 4a
2
{J
1
(2πaR/λf)/(2πaR/λf)}
2
. (10.29)
One has to simply replace the sin y/y function by the J
1
(y
)/y
function. We use
for R again Y and for R
the integration variable Y
. For the integral we then
have
I
im
(Y ) 4a
2
Y
b2
Y
b1
I
ob
(Y
)
J 1(2πa(Y − Y
)/λf )
(2πa(Y − Y
)/λf )
2
dY
. (10.30)
The calculation is shown in FileFig 10.5.
FileFig 10.5 (W5IMONEROS)
One round object and a circular lens. The image is obtained by convolution of
the object function with the spread function. The spread function is the Fourier
transformation of the pulse, representing the lens.
W5IMONEROS is only on the CD.
Application 10.5.
1. Change the diameter a of the lens to a smaller value than 25. What happens?
2. Change the diameter a of the lens to larger values than 25. At what value one
gets a good agreement with the object?
10.4.4.4 Two Round Objects and a Circular Lens
Two round objects of diameter 2b 0.004 and center-to-center distance bb
0.014, are treated in FileFig 10.6.
Since the system is linear, we have to calculate two integrals of the type
considered in Section 10.4.4.3 at the given distance.
I
im
(Y ) 4a
2
Y
b2
Y
b1
I
ob
(Y
)S(Y − Y
)dY
+ 4a
2
Y
b4
Y
b3
I
ob
(Y
)S(Y − Y
)dY
. (10.31)
The calculation is shown in FileFig 10.6.
10.4. IMAGE FORMATION USING INCOHERENT LIGHT 391
FileFig 10.6 (W6IMTWOROS)
Two round objects and a circular lens. The image is obtained by convolution of
each object function with the spread function. The spread function is the Fourier
transformation of the pulse, representing the lens.
W6IMTWOROS
Imaging: Two Round Apertures and Round Lens (R
is X)
Y :−.1, −.099.. 6 b1 ≡−.002 b2 ≡ .002 λ : .0005
Tol : .1 f/10 f/2a
f : 500 a : 25 b3 ≡ .012 b4 ≡ .016 k :
2 ·π
λ
.
Object
Io1(Y ): ((b2 − Y ) −(b1 −Y )) Io2(Y ): ((b4 − Y ) −(b3 − Y ))
lo(Y ): Io1(Y ) +Io2(Y ).
Image
lim(Y ):
b2
b1
4 · a
2
·
⎡
⎣
J 1
k·a(Y −YY)
f
k · a
(Y −YY)
f
⎤
⎦
2
dYY
+
b4
b3
4 · a
2
·
⎡
⎣
J 1
k·a·(Y −YY)
f
k · a ·
(Y −YY)
f
⎤
⎦
dYY.
