Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple
Подождите немного. Документ загружается.

9.2. FOURIER TRANSFORM SPECTROSCOPY 371
have
u
1
A(exp iπ)expi{2π (x
1
/λ − t/T)}. (A9.1)
The sample is assumed to be on the mirror in the movable arm of the interfer-
ometer, and we assume an amplitude reflection coefficient r and a phase change
ϕ. We call y the displacement from the equal path length position and have
u
2
A(r exp iϕ)expi{2π({x
1
+ y}/λ − t/T)}. (A9.2)
Superposition of the two waves gives us
u u
1
+ u
2
A{r exp iϕ + exp i{2πy/λ + (π)}exp i{2π(x
1
/λ − t/T)} (A9.3)
and for uu
∗
we calculate
uu
∗
A
2
{1 + r
2
+ 2r cos(ϕ −π − 2πy/λ)}. (A9.4)
Introduction of R for r
2
and for the frequency ν 1/λ, one has for the intensity
I ,
I (y) A
2
{1 + R + 2r cos(ϕ − π −2πyν)}. (A9.5)
If we have a continuous spectrum of frequencies ν,from0to∞ we have
I (y)
∞
∫
0
A
2
{1 + R + 2r cos(ϕ − π −2πyν)}dν. (A9.6)
For very large values of y the cosine term oscillates so fast that the average will
be zero. We call
I (∞)
∞
∫
0
A
2
{1 + R}dν (A9.7)
and get for Eq. (A9.6)
I (y) −I (∞)
∞
∫
0
A
2
{2r cos(ϕ −π − 2πyν)}dν. (A9.8)
Introduction of 2 cos x exp(ix) +exp(−ix) results in
I (y) −I (∞)
∞
∫
0
A
2
r{exp i(ϕ − π −2πyν) + exp −i(ϕ − π − 2πyν)}dν. (A9.9)
The difference in phase change for reflection on the sample (π − ϕ) may also
be written as (ϕ − π). The sign is of no importance. We can then factor out
exp i(ϕ − π ) and extend the frequency range formally to negative frequencies
(as done above in Section 2.3).
I (y) −I (∞)
∞
∫
−∞
{A
2
r exp i(ϕ − π )}{exp i(2πyν)}dν. (A9.10)
372 9. FOURIER TRANSFORMATION AND FT-SPECTROSCOPY
This is the Fourier transform integral in the frequency domain for the func-
tion {A
2
r(ν)expi(ϕ − π)}, and the corresponding Fourier transform integral in
coordinate space is
{A
2
r(ν)expi(ϕ − π )}
∞
∫
−∞
{I (y) −I (∞)}exp −i(2πyν)dν. (A9.11)
Equation (A9.11) is the Fourier transformation of the data {I (y) − I (∞)}. Per-
forming the Fourier transformation, we obtain for the integral in Eq. (A9.11) a
function of complexnumbers depending on ν, and call this function P (ν)−iQ(ν),
∞
∫
−∞
{I (y) −I (∞)}exp −i(2πyν)dν P (ν) −iQ(ν). (A9.12)
The background interferogram is obtained with a mirror in each arm of the
Michelson interferometer, and one has for the transformation
{A
2
r exp i(−π)}
∞
∫
−∞
{I
B
(y) − I
B
(∞)}exp −i(2πν)dν P
B
(ν) − iQ
B
(ν), (A9.13)
where r is assumed to be set to 1 because of the background. Dividing the
transformations of the sample and background interferogram we have
r(ν)expϕ(ν) {P (ν) − iQ(ν)}/{P
B
(ν) − iQ
B
(ν)}. (A9.14)
For the intensity reflection coefficient r
2
we then get
r
2
{P (ν)
2
+ Q(ν)
2
}/{P
B
(ν)
2
+ Q
B
(ν)
2
}. (A9.15)
Since the background spectrum is real, one may write
P (ν) −iQ(ν) (Realnumber) exp iϕ(ν) (A9.16)
and
tan ϕ Q(ν)/P (ν), (A9.17)
where the sign of ϕ, that is, its relation to 2π , has to be chosen.
The optical constants are obtained by using Fresnel’s formulas for normal
incidence and complex refractive index
r
2
{(1 −n)
2
+ K
2
}/{(1 + n)
2
+ K
2
} (A9.18)
and
tan ϕ (2K)/(n
2
+ K
2
− 1). (A9.19)
Explicit calculation of n and K results in
n (1 −r
2
)/(1 + 2r cos ϕ + r
2
) (A9.20)
K (−2r sin ϕ)/(1 + 2r cos ϕ +r
2
), (A9.21)
where the sign of ϕ is important in Eq. (A9.21).
9.2. FOURIER TRANSFORM SPECTROSCOPY 373
We have obtained from the Fourier transformation the complex numbers P (ν)
and Q(ν) and could use them to calculate r and ϕ. From Fresnel’s formulas we
calculate n and K.
See also on the CD
PF1. Fourier Transformation of the Gauss-Function. (see p. 332–333)
PF2. Fourier Transformation of the Functions 1/(1 + x
2
). (see p. 333)
PF3. Numerical Fourier Transformation. (see p. 334)
PF4. Step Functions.(see p.335)
PF6. Example of a Convolution Integral. (see p. 342)
PF7. Interferogram of Michelson interferometer. (see p. 350)
PF8. Folding of the Spectrum. (see p. 351)
PF9. Apodization. (see p. 359)

10
10
CHAPTER
Imaging
Using Wave Theory
10.1 INTRODUCTION
In geometrical optics we used the thin lens equation to find the image point of
an object point when using a thin lens of focal length f . Using wave theory we
assume that Huygens’ wavelets emerge from each point of the object and travel
to the lens. The lens produces the diffraction pattern of the object in its focal
plane, which may be seen as the Fourier transformation of the object pattern.
The lens also produces the image of the object by refraction. A second Fourier
transformation performed on the diffraction pattern results in a pattern having
the shape of the object. Since the light travels forward, we associate it with the
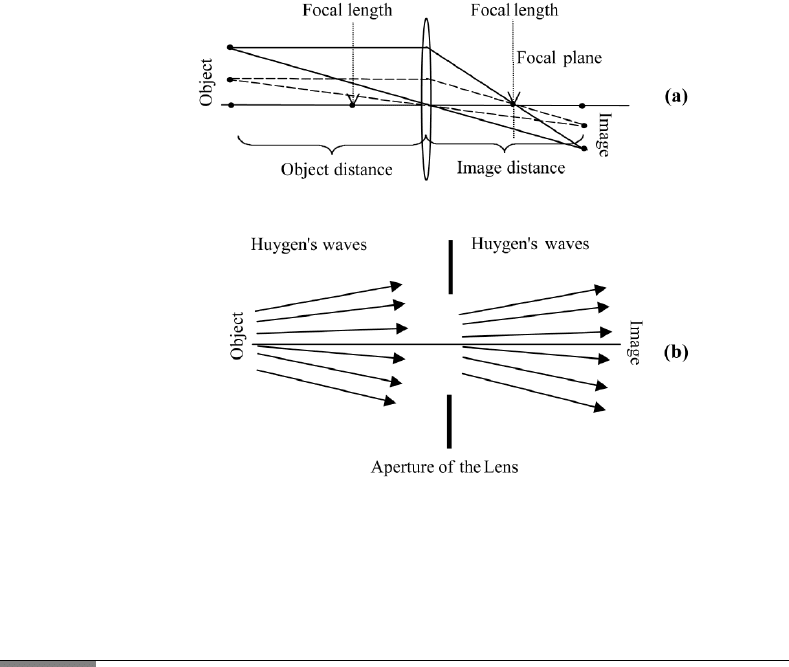
image. This is schematically shown in Figure 10.1.
The model we use for the description of image formation by a lens is, that
one Fourier transformation is applied to the object pattern to obtain the diffrac-
tion pattern of the object and a second Fourier transformation is applied to the
diffraction pattern to obtain the image pattern. Since we found that the Fourier
transform of a Fourier transform is the original, but know that experimentally
the image is not exactly the same as the object, we may ask the question, “Where
is the perturbation entering the process?” It has been one of the great discoveries
of optics (E. Abbe in Born and Wolf, 1964, xxi) that any perturbation of the
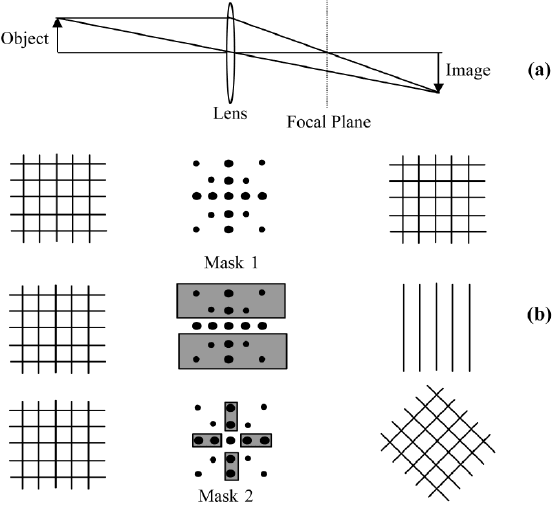
diffraction pattern modifies the image. In Figure 10.2 we show how changes in
the diffraction pattern, such as blocking off certain parts, change the image. We
may also introduce phase shifts at some spots and not at others and obtain an
image with much stronger contrast (F. Zernicke in Born and Wolf, 1964, xxi).
375
376 10. IMAGING USING WAVE THEORY
FIGURE 10.1 (a) The geometrical optical imaging process; (b) imaging process using wave theory.
The Huygens’ wavelets of the object generate the diffraction pattern, and the Huygens’ wavelets
of the diffraction pattern generate the image.
10.2 SPATIAL WAVES AND BLACKENING CURVES,
SPATIAL FREQUENCIES, AND FOURIER
TRANSFORMATION
Using scalar diffraction theory, the Kirchhoff–Fresnel integral uses monochro-
matic light to describe the diffraction pattern of the light emerging from the
object. A lens is used in Fraunhofer diffraction to have the diffraction pattern
observed in the focal plane of the lens. This same integral may be written as a
Fourier transform integral, as done in Chapter 3 for the diffraction on a slit. The
coordinates of the object, the slit, are length coordinates in the length domain.
The coordinates of the Fourier transformation, the diffraction pattern of the slit,
are coordinates in the spatial frequency domain and have 1/length dimensions.
We note that we deal with an amplitude diffraction pattern in the frequency do-
main, which contains phase information, even if we started with a real function
in the object plane. After one applies a second Fourier transformation on the
diffraction pattern (in the spatial frequency domain), the result is a geometrical
image pattern similar to the original object and appearing in the space domain.
In our model description we use the first Fourier transformation from the geo-
metrical space domain into the spatial frequency domain. The object is described
by geometrical spatial waves and the Fourier transformation describes the fre-
10.2. SPATIAL WAVES AND BLACKENING CURVES, SPATIAL FREQUENCIES, AND FOURIER TRANSFORMATION 377
FIGURE 10.2 (a) Schematic of image formation by geometrical optics, the focal plane is indicated;
(b) the object is a grid, the diffraction pattern is shown, and the image is again a grid. When masks
1 and 2 are placed at the focal plane of the lens, certain parts of the diffraction pattern are blocked
off. The resulting images are shown on the right.
quency spectrum of these spatial waves. The object function h(y) is interpreted
as a superposition of spatial waves and the result of the superposition is recorded
as the blackening of a photographic plate. The maxima of a spatial wave corre-
sponds to black, the minima corresponds to white, and the gray level indicates
zero. By doing so, we attribute phase information to these waves. Superposition
of a black maxima (+A) and a white minima (−A) results in gray (0). In the
section on holography, we present more details on the presentation of phase in-
formation with the black, white, and gray of the photographic plate. In FileFig
10.1 we show this concept in mathematical terms, considering the Fourier series
g(x)
N
n0
{
[4/((2n + 1)π)](sin 2π(f
n
x))
}
(10.1)
with frequencies f
n
(2n + 1)/2a, where a is a certain length constant in the
spatial domain.
The spatial waves with wavelengths
0
2a,
1
2a/3,
2
2a/5
correspond to spatial frequencies f
0
, f
1
, f
2
and are shown in FileFig 10.1. The
superposition of these three waves is also shown and one observes that the su-

378 10. IMAGING USING WAVE THEORY
perposition of a large number of such spatial waves results in a rectangular
shape.
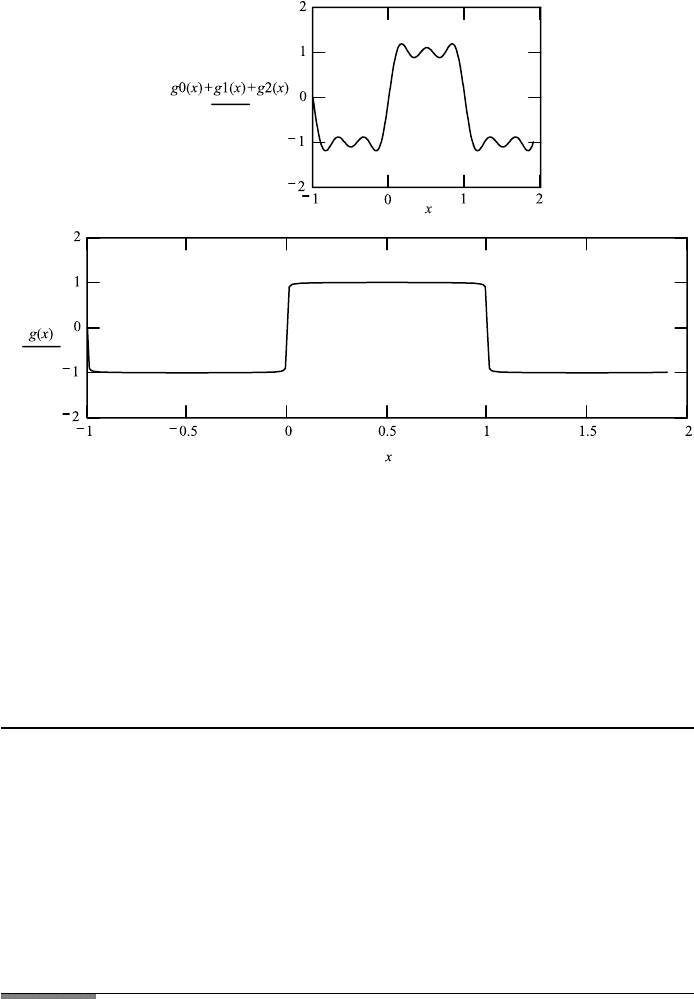
FileFig 10.1 (W1FTSERIS)
Fourier series of cosine functions for the composition of a rectangular-shaped
object. Different numbers of elements of the sum are plotted separately and as a
sum for comparison.
W1FTSERIS
Fourier Series of Spatial Wavelength λ for Interval from −1 to 1 (Shown to 2)
For N 0 the only term is a sine wave from −1 to 1, of wavelength λ 2.For
N 1 a sine term with 1/3 of λ and smaller amplitude is added. For N 2 a
term with 1/5 of λ and smaller amplitude is added, and so on. If N is large, we see
a perfect step function. For smaller N (in the 20th), we see Gibb’s phenomenon,
the corners are not round, and there is overshooting. For large N it disappears.
x :−1, −.99.. 1.9 : 1 n : 0, 1.. 200 N ≡ 100
g(x):
N
n0
4 · sin[2 · π ·x · (f
n
)]
(2 · n + 1) ·π
f
n
:
2 ·n + 1
2 ·
.
For larger and larger N one can see how more and more waves with shorter and
shorter wavelengths are used to build the step function.
g0(x):
4 · sin
π · x ·
1
π
g1(x):
4 · sin
π · x ·
2·1+1
(2 · 1 + 1) ·π
g2(x):
4 · sin
π · x ·
2·2+1
(2 · 1 + 1) ·π
.
10.2. SPATIAL WAVES AND BLACKENING CURVES, SPATIAL FREQUENCIES, AND FOURIER TRANSFORMATION 379
Application 10.1.
1. Use different values for N and NN and compare the resulting rectangular
pulse shape.
2. The deviation feature on the edges is called Gibb’s phenomenon. Observe the
appearance and disappearance of Gibb’s phenomena depending on N.
3. Change the sine functions to cosine functions and discuss the result.
In FileFig 10.2 we show schematically the calculation of the spatial frequency
spectrum, and the second Fourier transformation for image formation. We also
discuss the options for the second Fourier transformation. Could one use the
complex Fourier transformation again, or as we should, use the inverse Fourier
transformation?
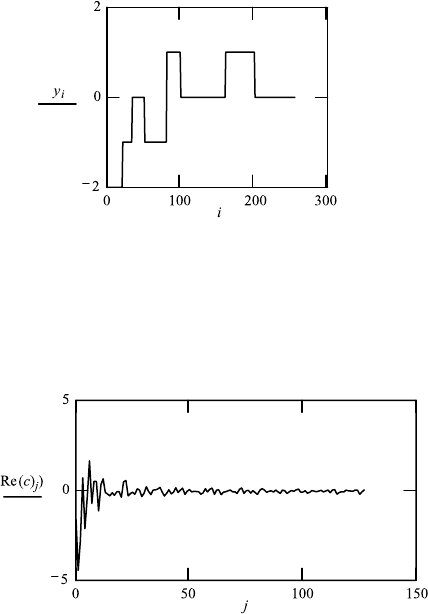
FileFig 10.2 (W2FTCFT)
Object is a composition of step functions. The complex Fourier transformation
and the inverse complex Fourier transformation are shown. The complex Fourier
transformation may be applied twice, but the image is interchanged left to right.
380 10. IMAGING USING WAVE THEORY
W2FTCFTS
Example of Real fft and Complex cfft on a Real Object Function
1. The real FT fft
The Object: i : 0, 1 ...255
A
1
: 33 A
3
: 80 A
4
: 50 A
5
: 20 A
6
: 99 A
7
: 160 A
8
: 200
y
i
:
3
n1
(−(A
n
− i)) +
8
n4
[(A
n
− i) · (−1)
n
].
The real Fourier transformation
c : ff t(y) Nc : last(c) Nc 128
j : 0 ...Nc− 1.
The inverse Fourier transformation
x : iff t ((c))
Nx : last(x)
Nx 255
k : 0 ...Nx − 1.
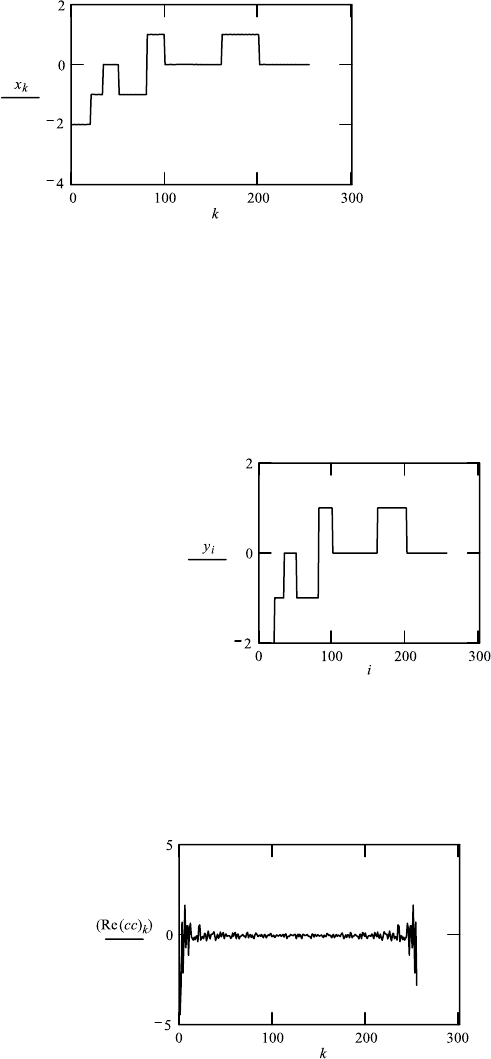
10.2. SPATIAL WAVES AND BLACKENING CURVES, SPATIAL FREQUENCIES, AND FOURIER TRANSFORMATION 381
We cannot use x ff t(c); we get the “Error message”; c must be real
2. The complex Fourier transformation
The Object: i : 0, 1 ...255
A
1
: 33 A
2
: 80 A
3
: 80 A
4
: 50 A
5
: 20
A
6
: 99 A
7
: 160 A
8
: 200
y
i
:
3
n1
(−(A
n
− i)) +
8
n4
[(A
n
− i) · (−1)
n
].
The complex Fourier transformation
cc : cf f t (y)
Ncc : last(cc) Ncc 255
k : 0 ...Ncc− 1.
