Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple
Подождите немного. Документ загружается.

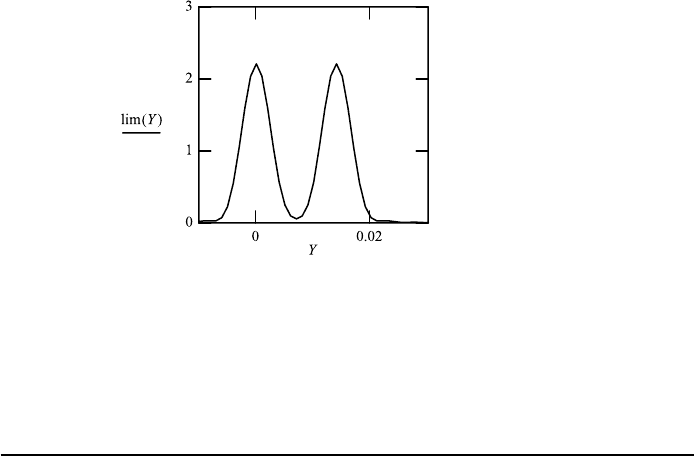
392 10. IMAGING USING WAVE THEORY
Unnormalized
Application 10.6.
1. Change the distance between the two object bars and study the resolution. If
the distance is too small, the image is just one peak.
2. Change the calculation and apply the spread function to the total image over
a large range of integration. The image is now closer to the object.
10.4.5 Transfer Function
10.4.5.1 Transfer Function and Fourier Transformation
The spread function is used in the coordinate space of the image to calculate
how the object appears on the observation screen (image coordinates). If the
lens did not alter the object we would observe a perfect image of the object. The
image was obtained by convolution of the object function I
ob
(Y
) with the spread
function S(Y − Y
), both using image space coordinates
I
im
(Y )
I
ob
(Y
)S(Y − Y
)dY
. (10.32)
From the convolution theorem we know that the integral in Eq. (10.32) expresses
the Fourier transform of the product of the Fourier transform of I
ob
(Y ) and the
Fourier transform of S(Y ). If we call these Fourier transforms
ω(µ)
I
ob
(Y
)e
−i2πµY
dY
(10.33)
and
τ (µ)
S(Y
)e
−i2πµY
dY
, (10.34)
one may write Eq. (10.32) as
I
im
(Y ) C
ω(µ)τ (µ)e
i2πµY
dµ, (10.35)

10.4. IMAGE FORMATION USING INCOHERENT LIGHT 393
where C contains all constants.
The Fourier transform of S(Y
), which is τ(µ), is called the (unnormalized)
transfer function. Equation (10.35) tells us that the Fourier transform of I
im
(Y ),
which we call φ
im
(µ), is equal to the product of the Fourier transforms ω(µ)τ(µ),
which is
φ
im
ω(µ)τ (µ). (10.36)
For the coordinates we have 1/Y µ, where µ may be interpreted as the spatial
frequency in the frequency domain. The transfer function operates in the spatial
frequency domain.
In FileFig 10.7 we calculate the Fourier transform of an object, which is a
rectangular pulse, and the Fourier transform of a spread function for a cylindrical
lens (transfer function). Then we multiply the Fourier transform of the object
with the transfer function and perform the Fourier transformation of the product.
The resulting image should look like a rectangular pulse.
FileFig 10.7 (W7PUTRAS)
Demonstration of the use of a transfer function. Object is a pulse and calcula-
tion of its Fourier transformation. Spread function and calculation of its Fourier
transformation. Product of both Fourier transformations and their Fourier trans-
formation (inverse). The resulting image of these operations looks like the
object.
W7PUTRAS is only on the CD.
10.4.5.2 Examples
Fourier Transform of (sin x/x)
2
as Transfer Function
We take as an object a grid presented as a series of square pulses (FileFig 10.8) and
calculate and perform the Fourier transformation ω
ob
(µ). The spread function
for a cylindrical lens is (Eq. (10.27)),
S(X) 4a
2
{sin(π X/λf #)/(πX/λf #)}
2
, (10.37)
where we use f # f/2a, for X (the space coordinate) i/255, and i is the
running number of the Fourier transformation from 1 to 256 (0-255). We have to
use here i/255 in the frequency domain since we used i in the space domain. The
Fourier transform of S(X)isτ (µ). The product of φ(µ) ω
ob
(µ)τ (µ) is shown
in FileFig 10.8, and the Fourier transform (inverse) of φ(µ) is the final image. In
FileFig 10.8 we have used the complex Fourier transform of 256 points for the
object and its mirror image. We should remember that the longest wavelength
of the spatial waves is 128, and the corresponding smallest frequency 1/128. We

394 10. IMAGING USING WAVE THEORY
also use the scale 1/256 in the transfer function and have the smallest frequency at
1/128. The wavelength is 0.0005 mm and the f # f/2a which is 10. Changing
the f # in FileFig 10.8 will change the triangle corresponding to τ
i
and will admit
more or fewer spatial frequencies for image formation.
FileFig 10.8 (W8TRASIS)
Demonstration of the use of a transfer function. Object is a grid and calculation
of it’s Fourier transformation. Spread function (sin y/y)
2
and calculation of
its Fourier transformation. Product of both Fourier transformations and their
Fourier transformation (inverse). The resulting image of these operations looks
more or less like the object.
W8TRASIS is only on the CD.
Application 10.8. Change the f # and observe through the changing triangle
that more or fewer frequencies are used for image formation.
Fourier Transformation of the Bessel Function as Transfer Function
We may use as the transfer function (J 1(y)/y)
2
corresponding to a circular
lens instead of (sin y/y)
2
, which corresponds to a cylindrical lens. Keeping the
argument of the transfer function the same but taking R instead of X we use
J 1(πR/λfn)/(πR/λfn), (10.38)
where fn is the f -number. The variable R is replaced by i/255 and i is the
running number of the Fourier transformation, from 1 to 256 (0–255). We have
to use here i/255 in the frequency domain, since we used i in the space domain. In
FileFig 10.9 the object is a grid presented as a series of square pulses in the space
domain, but the spread function is now (J 1(y)/y)
2
, and its Fourier transformation
is the transfer function τ (µ). The product of ω
ob
(µ)τ (µ) is calculated and shown
in FileFig 10.9. The Fourier transform (inverse) of φ(µ) ω
(
ob)(µ)τ (µ)isthe
final image.
Changing the f # in FileFig 10.9 will change τ
k
as shown and will admit more
or fewer spatial frequencies for image formation.
FileFig 10.9 (W9TRAJ1S)
Demonstration of the use of a transfer function. Object is a grid and calculation
of its Fourier transformation. Spread function (J 1(y)/y)
2
and calculation of
its Fourier transformation. Product of both Fouriers transformations and their

10.4. IMAGE FORMATION USING INCOHERENT LIGHT 395
Fourier transformation (inverse). The resulting image of these operations looks
more or less like the object.
W9TRAJ1S is only on the CD.
Application 10.9. Change the f # and observe through the changing transfer
function that more or fewer frequencies are used for image formation.
10.4.6 Resolution
The Rayleigh criterion of resolution states that two image peaks are considered
resolved if the maximum of the diffraction pattern of one is at the position of the
first minimum of the other. This is demonstrated in FileFig 10.10. We consider
two round objects and a round lens, and apply the Rayleigh criterion. The object
is made of two “rectangles" of width b1-b2 and b3-b4 (FileFig 10.11). The
aperture of the lens of diameter 2a forms a diffraction pattern of each point on
the image screen.
The argument of the Bessel function 2πaR/λf is again written as
πR/λ(f/2a) πR/λ(f #), (10.39)
where f # f/2a, and we use Y for R in FileFig 10.11. The first zero of the
Bessel function J
1
(πR
/λf #) is at πR
/λf # 3.83. Therefore if the maximum
of one peak is at the minimum of the other, the distance 2b
is (3.83/π )λf #
1.22λf #. In our example in FileFig 10.11 we have used the diameter 0.0005 mm
for the round objects, which is the same as the wavelength. The f # is equal to
10 and the product λf # has a value 0.005. The center-to-center distance of the
two objects is 0.0061. In FileFig 10.11 we show the image of the two objects at
the minimum distance corresponding to the resolution according to the Rayleigh
criterion.
FileFig 10.10 (W10BES3DS)
Demonstration of Resolution. Two Bessel functions in 3-D presentation of radius
a 0.05, center-to-center distance of d 24.5, wavelength λ 0.0005, and
distance to screen X 4000.
W10BES3DS
Rayleigh Distance and 3-D Graph for Two Round Apertures at Distance D
Radius of apertures is a, coordinate on the observation screen R, wavelength λ,
and distance from aperture to screen is X.
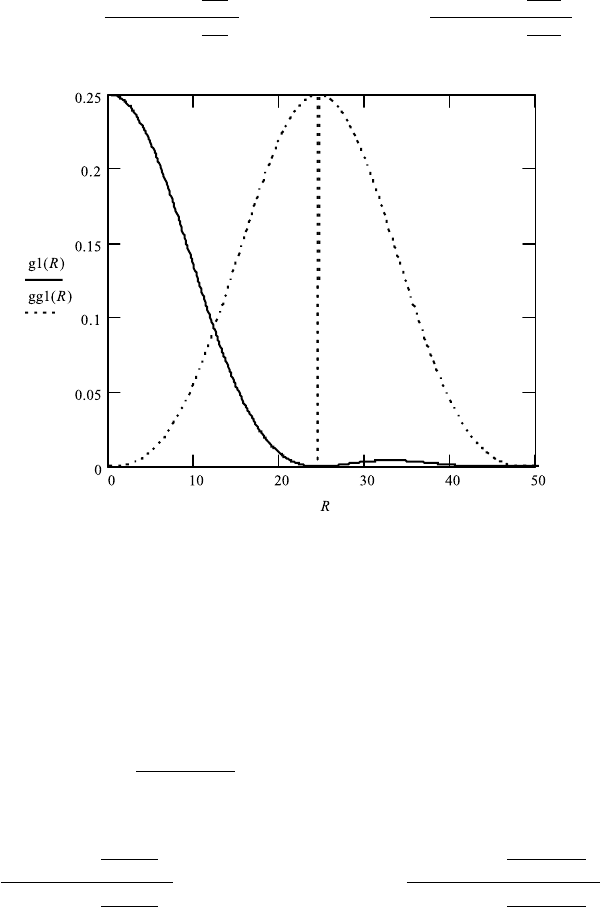
396 10. IMAGING USING WAVE THEORY
1. Determination of Rayleigh distance for two round apertures
a ≡ .05 X ≡ 4000 R : 0, 1 ...50
g1(R):
J 1
2 ·π · a ·
R
X·λ
2 ·π · a ·
R
X·λ
2
gg1(R):
J 1
2 ·π · a ·
R−d
X·λ
2 ·π · a ·
R−d
X·λ
2
2. 3-D Graph of pattern of two round apertures at distance d
i : 0 ...N j : 0 ...N
x
i
: (−40) + 2.000 · iyj: (−40) + 20001 · jλ≡ .0005
RR(x,y):
(x)
2
+ (y)
2
N ≡ 60 X : 4000
g2(x, y):
⎡
⎣
J 1
2 ·π · a ·
RR(x,y)
X·λ
2 ·π · a ·
RR(x,y)
X·λ
⎤
⎦
2
gg2(x,y):
⎡
⎣
J 1
2 ·π · a ·
RR(x,y−d)
X·λ
2 ·π · a ·
RR(x,y−d)
X·λ
⎤
⎦
2
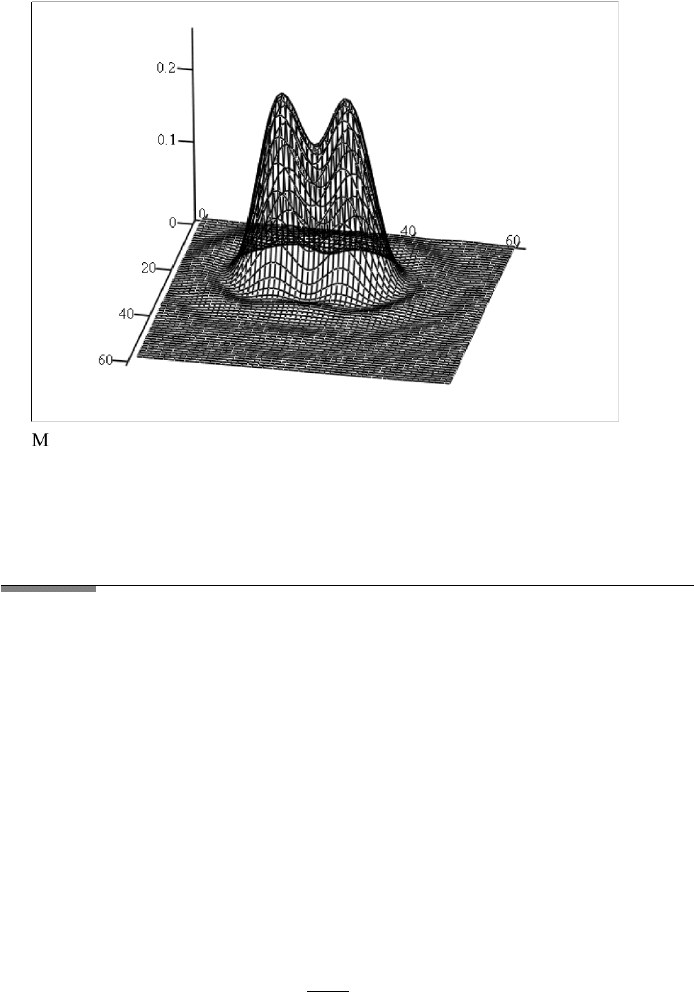
10.4. IMAGE FORMATION USING INCOHERENT LIGHT 397
M
i,j
: g2(x
i
,y
j
) + gg2(x
i
,y
j
) d ≡ 24.5.
FileFig 10.11 (W11TWOROJ1S)
Resolution. Two round objects at diameter 0.0005 and center-to-center distance
of 0.0061. The convolution with the spread function (J 1(y)/y)
2
results in a
resolved image.
W11TWOROJ1S
Imaging: Two Round Apertures as Objects
At Rayleigh distance, round lens, and Y used for R.
Object
Y :−.01, −.0099 ...02 λ : .0005 for choice of f# f/2a
Tol : .1 k :
2 ·π
λ
f : 500 a : 25
Io1(Y ): ((b2 − Y ) −(b1 −Y )) Io2(Y ): ((b4 − Y ) −(b3 − Y ))
Io(Y ): Io1(Y )
I
o2(Y ).
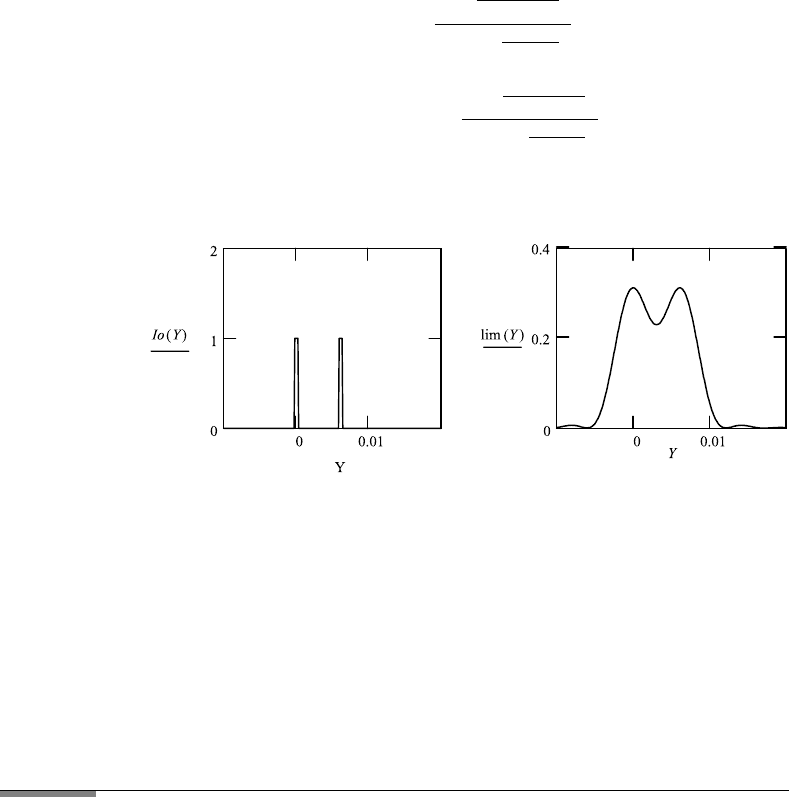
398 10. IMAGING USING WAVE THEORY
Image
lim(Y ):
b2
b1
4 · a
2
·
⎡
⎣
J 1
k·a·(Y −YY)
f
k · a ·
(Y −YY)
f
⎤
⎦
2
dYY
+
b4
b3
4 · a
2
·
⎡
⎣
J 1
k·a·(Y −YY)
f
k · a ·
(Y −YY)
f
⎤
⎦
2
dY.
Limits of integration
b1 ≡−.00025 b2 ≡+.00025 b3 ≡+.00585 b4 ≡+.00635.
Application 10.11.
1. Read the distance of the peaks of the image from the graph.
2. Change the distance between the objects so that the two are barely not
resolved.
3. Change the distance between the objects so that the two are barely separated.
4. Increase the size of the objects until they are no longer resolved.
10.5 IMAGE FORMATION WITH COHERENT LIGHT
10.5.1 Spread Function
We assumed in Section 10.4 that incoherent light is used for image formation.
We now discuss the image formation process using coherent light and show
that the spread function must be changed. The general process is the same as
in Section 10.4. Coherent radiation is now assumed to emerge from an object.
Using Huygens’ principle in the first process, the wavelets emerging from the
object are summed and travel to the lens. In the second process, the wavelets
emerging from the lens are summed. Taking the action of the lens into account
10.5. IMAGE FORMATION WITH COHERENT LIGHT 399
we found from Eq. (10.8) for the final image,
g(Y ) C
h(y)exp{−ikηy/x
0
}dy
α(η)exp{−ikηY/x
i
}dη, (10.40)
where the constant C before the integral takes care of all constant factors. Simi-
larly to the way we proceeded for the incoherent case, we use a δ function for a
point in the object plane. Substituting for h(y) a delta function into Eq. (10.40)
one obtains for the first Fourier transformation
δ(y)exp{−ikηy/x
0
}dy 1 (10.41)
and then has for the remaining part of the integral of Eq. (10.8),
s(Y ) C
α(η)exp{−ikηY/x
i
}dη. (10.42)
Equation (10.42) is the spread function s(Y ) for the case of coherent light. For the
image formation we again use a convolution integral, similar to the incoherent
case (see Eq. (10.21)) where h(Y ) describes the object. But unlike Eq. (10.21),
we use the spread function s(Y ), containing phase information. The convolution
integral
h(Y
)s(Y − Y
)dY
(10.43)
has to be squared for the description of the image
I
im
(Y ) |C
h(Y
)s(Y − Y
)dY
|
2
. (10.44)
In contrast to the incoherent case, we have to use s(Y ) for the spread function
instead of S(Y ), which is s(Y )
2
. The spread function is first convolved with all
points of the object and then we have to square the integral to get the image.
10.5.2 Resolution
As an example we discuss the problem of resolution. We consider two round ob-
jects of diameter 0.0005 mm, as we did for the incoherent case, and a wavelength
of 0.0005 mm and a f # 10. The distance to be determined should be such
that the final image looks similar to the image of the two objects as we found
for the incoherent case, when applying the Rayleigh criterion. The calculation
is presented in FileFig 10.12.
The image is calculated from the convolution integrals, where we call h(Y )
here iob(Y ) and omit the constants before the integral,
I
im
(Y )
Y
b2
Y
b1
iob(Y
)s(Y − Y
)dX
+
Y
b4
Y
b3
iob(Y
)s(Y − Y
)dY
2
.
(10.45)

400 10. IMAGING USING WAVE THEORY
We use for s(Y ) the Bessel function similar to Eq. (10.38). The intensity of the
image is obtained by squaring the result of the integration (note that s(Y − Y
)
contains phase information).
The distance of the two peaks in the final image of the two objects for the
coherent case is at a center-to-center distance of 0.0082. This is larger than for
the incoherent case. The final image is shown for the same distance as used for
the incoherent case, and one observes that the two peaks are not resolved. Since
the distance used in the coherent case is larger than the one for the incoherent
case, for a comparable set of parameters, we have the result: Better resolution is
obtained by using incoherent light.
FileFig 10.12 (W12TWOROCOHS)
Two round objects of diameter 0.0005 and center-to-center distance of 0.0061,
as used for the incoherent case. The convolution with the spread function,
(J 1(y)/y), results in an image of one peak, not resolved. For larger center-
to-center distance, 0.0082, the peaks are resolved.
W12TWOROCOHS
Imaging with Coherent Light
Two round apertures at Rayleigh distance, round lens, and Y used for R
.
Y :−.01, −.0099 ...02 λ : .0005 f/10 f/2a
To1: .1 k :
2 ·π
λ
f : 500 a : 25.
Object Amplitudes
iob(1) : ((b2 − Y ) − (b1 − Y )) iob2(Y ): ((b4 − Y ) −(b3 − Y ))
iob(Y ): iob1(Y ) +iob2(Y ).
Image
lim(Y ):
⎡
⎣
b2
b1
4 · a
2
·
⎡
⎣
J 1
k·a·(Y −YY)
f
k · a
(Y −YY)
f
⎤
⎦
dYY
+
b4
b3
4 · a
2
·
⎡
⎣
J 1
k·a·(Y −YY)
f
k · a ·
(Y −YY)
f
⎤
⎦
dYY
⎤
⎦
2
.
Integration limits
b1 ≡−.00025 b2 ≡+.00025 b3 ≡+.00585 b4 ≡+.00635.
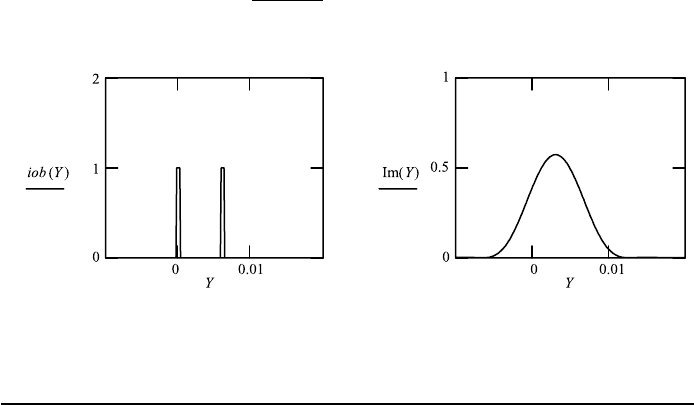
10.5. IMAGE FORMATION WITH COHERENT LIGHT 401
b4 − b3
2
+ b3 6.1 ·10
−3
.
Resolution is obtained for b3 .00795, b4 .00845.
Application 10.12. Introduce the center-to-center distance of 0.0082 between
the two objects, b3 0.00795 and b4 0.00845 and show that the two objects
appear resolved.
10.5.3 Transfer Function
We proceed much as we did in the incoherent case and call
ω(µ)
iob(Y
)e
−i2πµY
dY
(10.46)
and
˜τ (µ)
s(Y
)e
−i2πµY
dY
, (10.47)
where ˜τ (µ) is the transfer function in the coherent case. The difference in
Eq. (10.47) with respect to Eq. (10.34) is that s(Y
) is an amplitude function
that carries phase information. The image is obtained by a Fourier transforma-
tion, similar to Eq. (10.35) for the incoherent case. To obtain the description of the
intensity of the image, the result has to be squared. We have for the coherent case
I
im
(Y ) |C
ω(µ) ˜τ(µ)e
i2πµY
dµ|
2
. (10.48)
We call φ
im
(µ) the Fourier transformation of I
im
(Y ) and get
I
im
(Y ) {FT of the product of the FT of I
ob
and FT ofs}
2
. (10.49)
In the frequency domain we have, similar to Eq. (10.36),
φ
im
(µ) {ω(µ) ˜τ(µ)}. (10.50)
Comparing (10.50) with (10.36) one sees that a symmetric blocking function
that does not carry phase information has the same effect of eliminating certain
spatial frequencies for the incoherent and coherent cases.
