Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple
Подождите немного. Документ загружается.


402 10. IMAGING USING WAVE THEORY
As examples we consider the imaging of a periodic structure using the spread
functions (sin y/y) and (J 1(y)/y). For the coherent case we use in FileFig 10.13
the spread function (sin y/y) in comparison to the incoherent case of FileFig 10.8
where we used (sin y/y)
2
. In FileFig 10.14 the spread function (J 1(y)/y) is used
in comparison to FileFig 10.9 where we used (J 1(y)/y)
2
. For the coherent case
the spread functions are not squared. The final image has to be the square of
the last Fourier transformation (see Eq. (10.48)). In comparison one sees that
the transfer function (i.e., τ ) eliminates in the incoherent case higher spatial
frequencies in a linear way and in the coherent case in a steplike fashion.
The transfer function τ in FileFig 10.13 is a pulse function and may be inter-
preted as a blocking function, eliminating parts of the diffraction pattern of the
object. Similar action was taken in Figure 10.2 on the diffraction pattern in order
to change the image.
FileFig 10.13 (W13TRANCOHSIS)
Coherent case. Transfer function for (sin x/x). Object is a grid and calcula-
tion of its Fourier transformation. Spread function (sin x/x) and calculation of
its Fourier transformation. Product of both Fourier transformations and their
Fourier transformation (inverse). The image as a result of these operations looks
more or less like the object.
W13TRANCOHSIS is only on the CD.
Application 10.13.
1. Change the f #; that is, change the width of the spread function and observe
that more or fewer frequencies are used for image formation.
2. Compare the incoherent and coherent cases for the same f #. Choose one
larger and one smaller f #.
FileFig 10.14 (W14TRANJ1S)
Coherent case. Transfer function for (Bess/arg). Calculation of the trans-
fer function for the coherent case. Object is a grid and calculation of its
Fourier transformation. Spread function (Bess/arg) and calculation of its Fourier
transformation. Product of both Fourier transformations and their Fourier trans-
formation (inverse). The image as a result of these operations looks more or less
like the object.
W14TRANJ1S is only on the CD.
10.6. HOLOGRAPHY
403
Application 10.14.
1. Change the f #; that is change the width of the spread function and observe
that more or fewer frequencies are used for image formation.
2. Compare the incoherent and coherent cases for the same f #. Choose one
larger and one smaller f #.
10.6 HOLOGRAPHY
10.6.1 Introduction
When discussing the imaging process for coherent light, the first Fourier trans-
formation produced the diffraction pattern of the object. The result of the first
Fourier transformation contained phase information, regardless of whether the
object was a real or complex function. The second Fourier transformation needed
this phase information to produce the image of the object. To fix the phase infor-
mation on a photographic plate we follow closely the discussion in Goodmann,
1988, p.198.
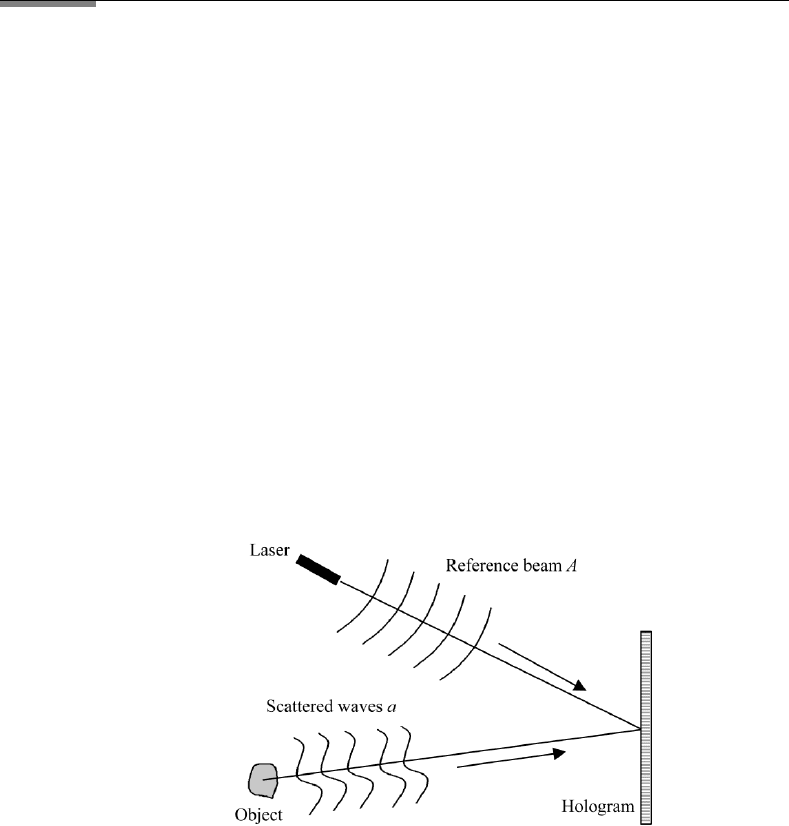
10.6.2 Recording of the Interferogram
In holography one uses a photographic film to record the amplitude and phase
information necessary for the reconstruction of the image of an object. This
is done by interference of the coherent light, scattered from the object with a
coherent reference beam (Figure 10.5).
The light scattered by the object is described by the complex amplitude func-
tion a a
0
e
−iφ
, where a
0
is a function of y, z and φ a function of x, y, z. The
reference wave is described by the complex amplitude function A A
0
e
−iψ
,
FIGURE 10.5 Production of a hologram. The interference pattern, produced by the waves of the
scattered light a of the object and the light of a reference beam A, is recorded on a photographic
film, called the hologram.
404 10. IMAGING USING WAVE THEORY
where A
0
is a constant and ψ contains the coordinates describing the direction
of incidence and propagation with respect to the photographic film.
The intensity pattern of the interference of A and a is
|A + a|
2
A
2
0
+ a
2
0
+ A
0
a
0
e
−iφ
e
i
+ A
0
a
0
e
iφ
e
−iψ
A
2
0
+ a
2
0
+ 2A
0
a
0
cos(φ − ψ ). (10.51)
The interference pattern is recorded on the photographic film and after develop-
ment the phase information is contained in the profile of the density of blackening.
The relation between the intensity of the light incident on a spot of the film and
the resulting blackening is logarithmic. A detailed discussion of the resulting
transmission t of the film, which is called a hologram, is presented in Goodmans
(1988). Under certain circumstances one can describe the transmission curve in
a linear way and have
t
film
cA
2
0
+ β
a
2
0
+ β
A
0
a
0
e
−iφ
e
iψ
+ β
A
0
a
0
e
iφ
e
−iψ
(10.52)
where c and β
are constants. The third and fourth terms are each complex.
However, together they are real and therefore t
film
remains real.
10.6.3 Recovery of Image with Same Plane Wave Used for
Recording
10.6.3.1 Virtual Image
We illuminate the hologram with a plane wave equal to the one used for the
recording of the hologram. We use in Eq. (10.53) A
0
e
−iψ
and in Eq. (10.54) the
conjugate A
0
e
i
and have
A
0
e
−iψ
t
film
A
0
e
−iψ
(cA
2
0
+β
a
2
0
+β
A
0
a
0
e
−iφ
e
iψ
+β
A
0
a
0
e
+iφ
e
−iψ
) (10.53)
A
0
e
iψ
t
film
A
0
e
iψ
(cA
2
0
+β
a
2
0
+β
A
0
a
0
e
−iφ
e
iψ
+β
A
0
a
0
e
+iφ
e
−iψ
). (10.54)
The first term in Eqs. (10.53) and (10.54) is a constant term; the second may be
neglected if we assume that a
0
is small compared to A. The third term in (10.53)
is
A
0
e
−iψ
β
A
0
a
0
e
−iφ
e
iψ
(β
A
2
0
)a
0
e
−iφ
. (10.55)
This is the important term for the virtual image. It is the doublet of the wavefront
of the original and diverges. In Figure 10.6a. we show the recovery of the image
using the beam A. As we know from geometrical optics, the diverging light is
traced back to a virtual image of the object.
10.6.3.2 Real Image
Similarly in Eq. (10.54) the fourth term is
A
0
e
iψ
β
A
0
a
0
e
iφ
e
−iψ
(β
A
2
0
)a
0
e
iφ
(10.56)
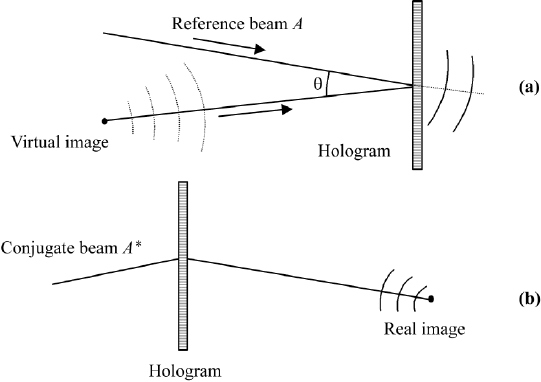
10.6. HOLOGRAPHY 405
FIGURE 10.6 Recovery of the image: (a) reference beam A illuminates the hologram; wavefront
of image diverges. It is traced back to the virtual image (reversed operation of production of
hologram); (b) reference beam A
∗
illuminates the hologram; wavefront of image converges to the
real image.
and is the duplication of the conjugate of the wavefront of the original. In Fig-
ure 10.6b we show the illumination by the beam A
∗
and the convergence to the
real image, which is in the opposite direction to the virtual image we discussed
in Section 10.6.3.1.
10.6.4 Recovery Using a Different Plane Wave
If we produce the hologram with a plane wave of amplitude A and illuminate
the hologram with a plane wave of amplitude B, all in the same (horizontal)
direction, we get
B
0
t
film
cB
0
A
2
0
+ dB
0
a
2
0
+ β
B
0
A
0
a
0
e
−iφ
+ β
B
0
A
0
a
0
e
iφ
. (10.57)
The real and virtual image now both appear in the horizontal direction (see
Figure 10.7).
10.6.5 Production of Real and Virtual Image Under an Angle
To see the virtual image separately from the real image, one has to use a reference
wave under an angle with respect to the normal of the object, around which the
scattered light emerges. To do this, we use for A the wave A
0
e
−i2π sin θ(x/λ)
and
have for the transparency of the film
t
film
cA
2
0
+ β
a
2
0
+ β
A
0
a
0
e
−iφ
e
i2π sin θ(x/λ)
+ β
A
0
a
0
e
iφ
e
−i2π sin θ(x/λ)
. (10.58)
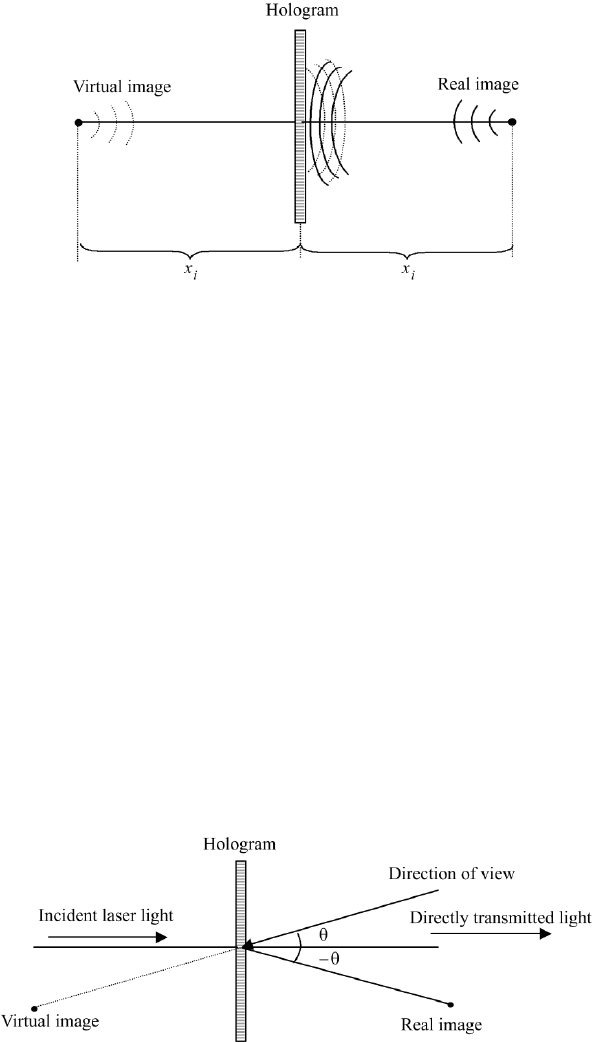
406
10. IMAGING USING WAVE THEORY
FIGURE 10.7 Real and virtual image appear in one direction, the direction of view.
For recovery we illuminate with a plane wave of amplitude B. Going through
the same discussion as presented above, we get for the third (Eq. (10.59)) and
fourth terms (Eq. (10.59)a)
(β
A
2
0
)a
0
e
−iφ
e
+i2π sin θ(x/λ)
(10.59a)
and
(β
A
2
0
)a
0
e
iφ
e
−i2π sin θ(x/λ)
. (10.59b)
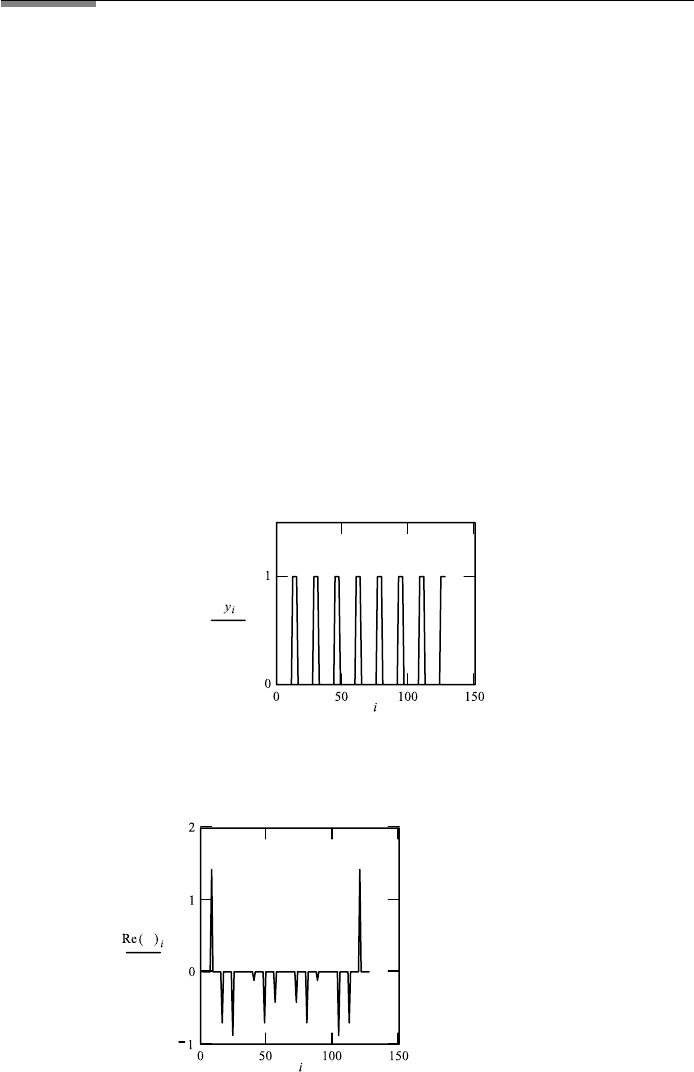
The virtual image Eq. (10.59a) is now (after tracing backwards) in the direction
of θ. The real image is in the direction of −θ and that is different from the
direction we seek for the virtual image. This is shown in Figure 10.8, where
virtual and real images are separated.
10.6.6 Size of Hologram
In the discussion of imaging we found that for a special case using coherent
light the image can be calculated from the Fourier transform of the Fourier
transform of the object. The hologram may be compared, in a simplified way,
FIGURE 10.8 The incident light is from the left and directly transmitted light continues to the
right. The direction of view is at the angle θ, and the virtual image is traced back in that direction.
The real image appears on the right at the angle − θ .

10.6. HOLOGRAPHY 407
with the diffraction pattern of the object. It contains the spatial frequency spec-
trum including phase information. We may then substitute for the hologram the
Fourier transform of the object and obtain the image is by a second Fourier
transformation.
Using this simple model we can easily demonstrate that the object can be
reconstructed using different sizes of the hologram. Smaller physical sizes will
give us more deteriorated images of the object. By cutting a large hologram into
small ones, we lose spatial frequency information. For simplicity we consider an
object with the first Fourier transformation in such a way that the smallest fre-
quencies are in the center and the largest frequencies at increased distances from
the center. To demonstrate the effect of the removal of frequencies we consider
the example of a grid as an object. Removing certain sections of the frequency
pattern, which is accomplished with the first Fourier transformation, will change
the image. In FileFig 10.15 we use a blocking function for a low frequency
portion, in FileFig 10.16 a blocking function for an intermediate section, and in
FileFig 10.17 a blocking function of a grid. In FileFig 10.18 we simulate cutting
down the hologram by a blocking function, which symmetrically cuts down the
lowest frequencies.
FileFig 10.15 (W15HOGRBLHIS)
The object is a grid. The transfer function removes certain higher frequencies of
the first Fourier transformation. The extent of the blocking function depends on
a. The modified image is compared with the original object.
W15HOGRBLHIS is only on the CD.
Application 10.15. Observe the changes of the final image by modification of
the blocking function, that is, changing a.
FileFig 10.16 (W16HOGRBLLOS)
The object is a grid. The transfer function is a blocking function passing only
one portion of the frequencies of the first Fourier transformation. The extent of
the blocking function depends on n and a. The modified image is compared to
the original object.
W16HOGRBLLOS is only on the CD.
Application 10.16. Observe the changes of the final image by modification of
the blocking function, that is, changing n and a.
408 10. IMAGING USING WAVE THEORY
FileFig 10.17 (W17HOGRPERS)
The object is a grid. The transfer function is a grid-type blocking function block-
ing periodic parts of the first Fourier transformation. The width of the peaks and
the extent of the blocking function depend on q and a. The modified image is
compared to the original object.
W17HOGRPERS
Object Is a Periodic Structure
The FT of the object is multiplied by a blocking function. A blocking function
has been chosen blocking certain frequencies such that there are twice as many
peaks in the image. The Ft (inverse) of (Ft of object) · (blocking function) is the
“new” image. The “new” image is compared to the original, that is, the FT of
(FT of object). The blocking function removes certain high frequencies of the FT.
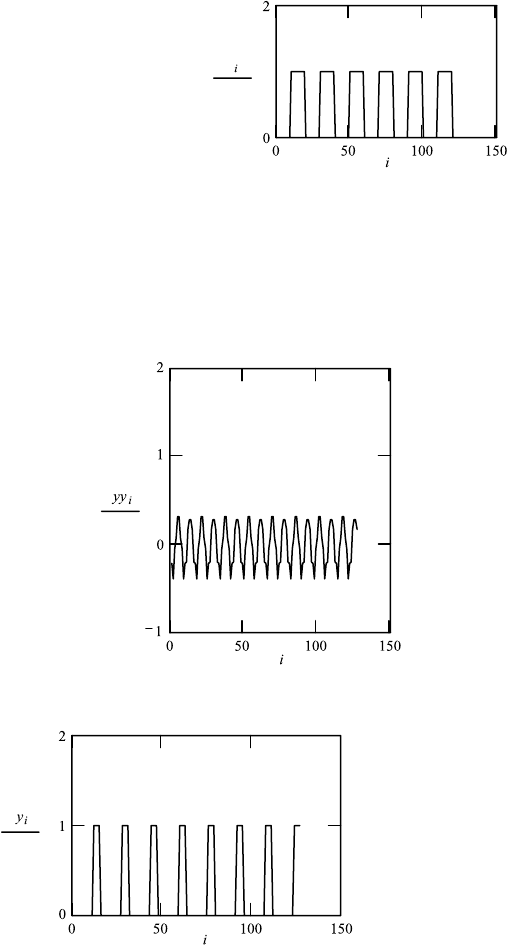
Object
i : 1, 2 ...127 b : 2 q : 7
y
i
:
q
n0
((i − (4 · (2 · n + 1) + 2) · b) − (i −(4 ·(2 · n + 1) + 4) · b))
.
FT of object
ω : cff t (y) N : last(ω)
N 127.
w
10.6. HOLOGRAPHY 409
Blocking function
τ
i
:
q
n0
((i − (4 · n + 2) · a) −(i − (4 · n + 4) · a))
q ≡ 5 a ≡ 5.
t
Product: FT (inverse) of object and blocking function
φ
i
: ω
i
· τ
i
yy : icfft(φ)
N2: last(φ)
k : 0 ...N2.
For comparison: original object
410 10. IMAGING USING WAVE THEORY
Application 10.17. Observe the changes of the final image by modification of
the blocking function, that is, changing q and a.
FileFig 10.18 (W18HOSTEPS)
The object is a step function composition. The transfer function passes the lowest
frequencies on both parts of the diffraction pattern, that is, the first Fourier
transformation. The number of passing lowest frequencies is monitored by a
and b. The hologram is larger when more frequencies are passing. The modified
image is compared to the original object.
W18HOSTEPS
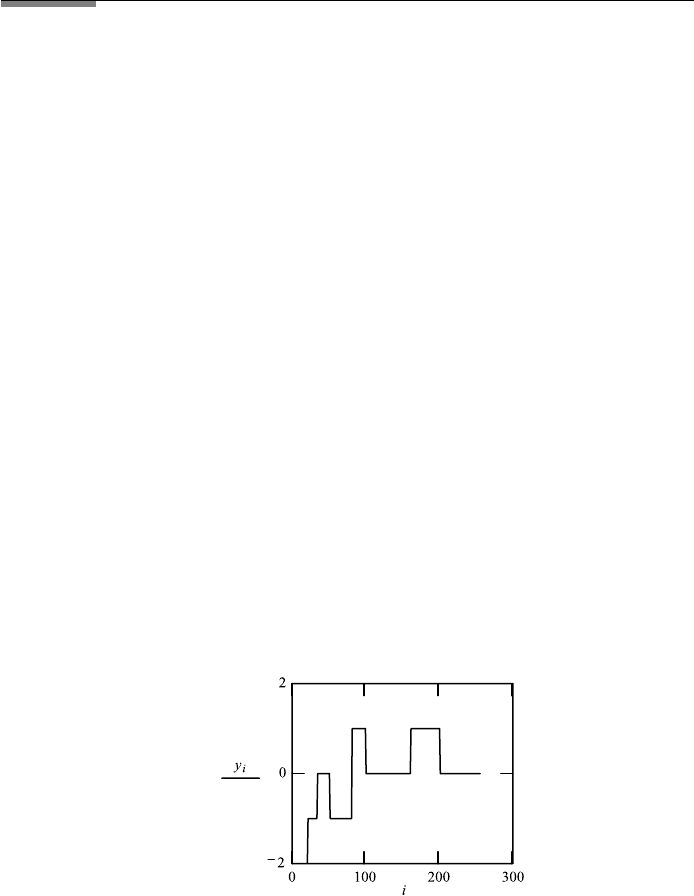
Object y
The object y has a complicated shape. Its FT is the hologram c. It may be
produced in the focal plane of a lens, using parallel light. The illumination of the
hologram with parallel light will reproduce the object, that is, the FT (inverse) of
the FT, called here cc. We study the reproduced object when the information in
the hologram is only partly used; that is, we multiply cc with a filder f . We show
separately f and the FT of the product of f and cc. The width of the filter f may
be changed by using various values for a and b, corresponding to changing the
size of the hologram.
The object i : 0, 1 ...255.
A
1
: 33 A
2
: 80 A
3
: 80 A
4
: 50
A
5
: 20 A
6
: 99 A
7
: 160 A
8
: 200
y
i
:
3
n1
(−(A
n
− i))
+
8
n4
[(A
n
− i) · (−1)
n
]
.
The hologram
c : cff t (y)N : last(c) N 255
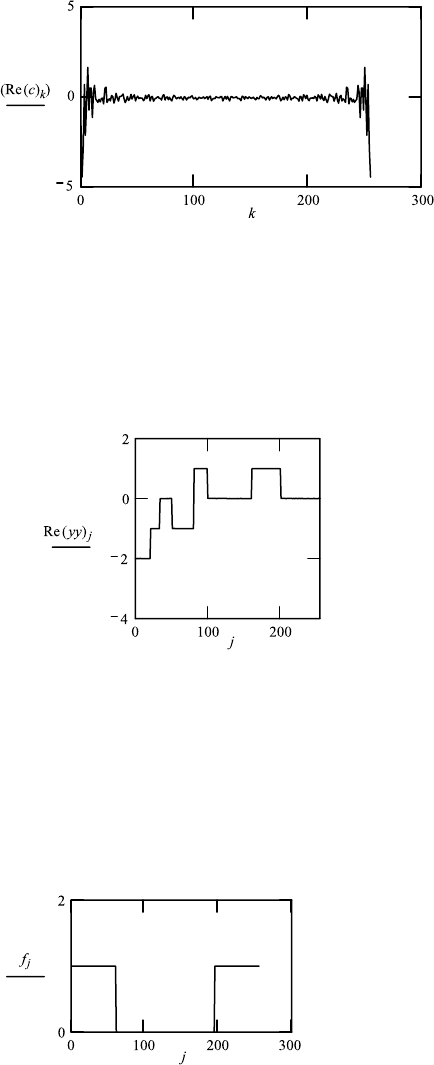
10.6. HOLOGRAPHY 411
k : 0 ...255 j ≡ 0 ...255
The inverse FT of the FT (hologram)
cc
k
: c
k
yy : icfft(cc)
N : last(cc) N 255 j : 0 ...255
The filter
f
j
: (a − j) +(j − 255 +b)
a ≡ 60
b ≡ 60.
