Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple
Подождите немного. Документ загружается.


9.2. FOURIER TRANSFORM SPECTROSCOPY 361
c : ff t(y1)
N : last(c) N 128
j : 0 ...128
Frequency peaks are at 65, 85, 105.
2. Sample interval 2i/255
For the sampling interval 2/255, highest frequency is 64: the original
frequencies are at 65, 85, 105: they are all larger 64 and appear folded.
y2
i
: cos
2 ·π · 65
2 ·i
255
+ cos
2 ·π · 85 ·
2 ·i
255
+ cos
2 ·π · 105
2 ·i
255
.
c : ff t(y2)
N : last(cc) N 128
362 9. FOURIER TRANSFORMATION AND FT-SPECTROSCOPY
j : 0 ...128
Frequency peaks appear at 45, 85, 125.
3. Sample interval 4i/255
For the sampling interval 4/255, highest frequency 32, the frequencies are
higher than 1 times 32 and 2 times 32.
y4
i
: cos
2 ·π · 65
4 · i
255
+ cos
2 ·π · 85 ·
4 · i
255
+ cos
2 ·π · 105
4 · i
255
.
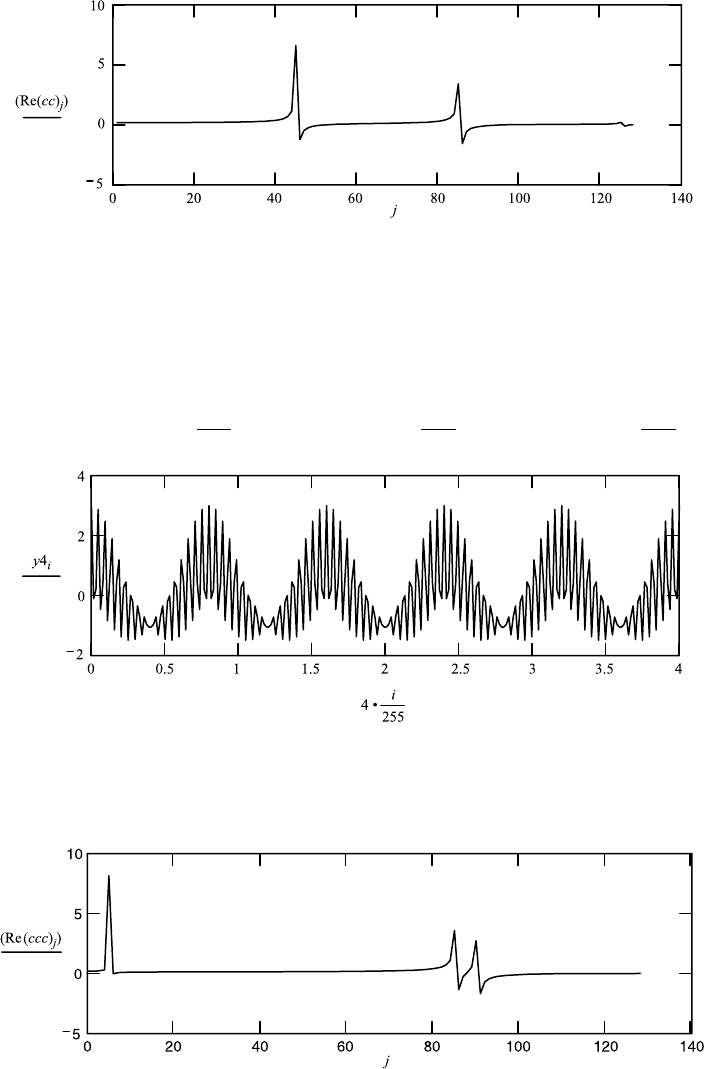
ccc : ff t(y4)
N : last(ccc) N 128
j : 1 ...128

9.2. FOURIER TRANSFORM SPECTROSCOPY 363
Freguency peaks appear
65 at → 125
85 at → 185
105 at → 45.
Application 9.15. Use the three frequencies 15, 34, and 97. Determine the ap-
pearance in the Fourier transformation as discussed for the original set (65, 85,
105) of frequencies.
9.2.6 High Resolution Spectroscopy
In high resolution spectroscopy one is often interested in investigating a nar-
row bandwidth of frequencies for high resolution. The sampling interval l in
the length domain is related to the highest frequency ν
M
in the 1/length domain.
When increasing the number of points N in the length domain, one also increases
the number N of points in the frequency domain. Since the sampling interval
determines the frequency interval from 0 to ν
M
, a higher number of points in the
length domain results in a higher number of points in the frequency domain. One
gets higher resolution in the interval from 0 to ν
M
. The resolution is inverse pro-
portional to the total length L of the interferogram. The length may be expressed
as L Nl, and one has
Nl L 1/(2(ν
M
/N)) (9.64)
and obtains for ν
M
/N
ν
M
/N ν 1/2L. (9.65)
A high resolution interferometer uses a large optical path difference L in order to
make ν small. If we take, for example, L 50 cm, we have for ν (1/100)
cm
−1
and for the resolving power R ν
M
/ν at 100 microns (equal to 100
cm−1)
R ν
M
/ν 100/(1/100) 10, 000. (9.66)
The number of points in length space is equal to the number of frequency intervals
in frequency space, which is
N 100/(1/100) 10, 000 (9.67)
and is also equal to R. To record 10,000 points, assuming about 3 sec for each
point, would take 9 hours. The information we obtain in this way is a spectrum
from 1 to 100 cm
−1
with resolution of 1/100 cm
−1
.
In the case where one is only interested in the study of a section of the spectrum
one may use folding of the spectrum. Let us assume that we are interested in
the section from 2/3 of 100 cm
−1
to 100 cm
−1
. In that case we use a bandpass

364 9. FOURIER TRANSFORMATION AND FT-SPECTROSCOPY
FIGURE 9.2 We assume that a bandpass filter eliminates the spectrum from 1 to 66 cm
−1
. The
spectrum is folded by using a sampling interval of 3 times l, where l is the sampling interval,
corresponding to the highest frequency 100 cm
−1
; that is, 1 1/2 · 100 cm
−1
0.005 cm 50
microns. The frequency scale for the sections changes the direction to the highest value for even
or odd factors of folding.
filter and eliminate all other frequencies, and fold the spectrum three times by
choosing a sample interval three times larger (see Figure 9.2). This is similar to
what we discussed above in FileFig 9.15, where we studied the folding of a sum
of cos-functions sampled with intervals 1/256, 2/256, and 4/256.
We have ν
M
/3 for the width of the spectral sections to be studied with the
length L of the interferogram. Consequently, the sampling interval has the value
3 l L/3333, instead of l L/(10, 000). The total number of points is reduced
from 10,000 to 3333, but the length of the interferogram remains the same.
Therefore we obtain the same high resolution in a smaller spectral region with
one-third of the points. A very important fact is that we have to use the bandpass
filter we assumed to apply. The spectra of the two sections of 1 to 33 cm
−1
and 33
cm
−1
to 66 cm
−1
are folded onto the spectrum of 66 cm
−1
to 100 cm
−1
. If they
contain spectral information, the spectrum will be “messed up," like the Fourier
transforms in FileFig 9.15. We obtain the same high resolution for a smaller part
of the spectrum, using a larger sampling interval and fewer points. In our case
the spectrum is obtained in one-third of the time.
In Figure 9.3 we show the background spectrum, taken with a Michelson inter-
ferometer and a bandpass filter. The bandpass has to have a width of ν
M
/integer.
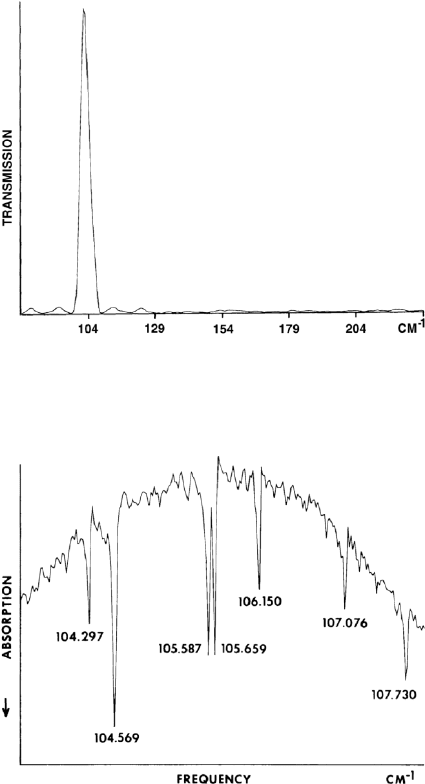
9.2. FOURIER TRANSFORM SPECTROSCOPY 365
FIGURE 9.3 The background spectrum taken with a Michelson interferometer and a bandpass
filter. (From J. Kachmarsky et al., Far-infrared high-resolution Fourier transform spectrometer:
applications to H
2
O, NH
3
, and NO
2
lines. Applied Optics, 15, 1976, p 708–713.)
FIGURE 9.4 High-resolution spectrum of water in the 104 to 107 cm
−1
region obtained by folding
the spectrum six times. (From J. Kachmarsky et al., Far-infrared high-resolution Fourtier transform
spectrometer: applications to H
2
O, NH
3
, and NO
2
lines. Applied Optics, 15, 1976, p 708–713.)
In Figure 9.4 we show a high-resolution spectrum of water in the 104 to 107
cm
−1
region, obtained with a sampling interval six times larger and in a time
span six times shorter. We state the procedure in more general terms as follows.A
filter is used to eliminate all parts of the spectrum with frequencies higher than
ν
M
and lower than ν
m
, where m stands for minimum. The value of ν
m
has to be
chosen in such a way that q ν
M
/(ν
M
−ν
m
) is an integer. We then obtain with
N sample intervals, each calculated by using
l 1/{2(ν
M
− ν
m
)}, (9.68)
366 9. FOURIER TRANSFORMATION AND FT-SPECTROSCOPY
a spectrum of width ν
M
/q and a resolution of ν 1/(2L), where L Nl.
The scale has its highest value ν
M
/q and runs forward for q odd and backward
for q even (Figure 9.2).
9.2.7 Apodization
The Fourier integrals, as shown in Eq. (9.55) and (9.56),
S(y) 2
∞
∫
0
G(ν){cos(2πνy)}dν (9.69)
G(ν) 2
∞
∫
0
S(y){cos(2πνy)}dy (9.70)
have a range of integration from 0 to ∞. The discrete Fourier transform, as shown
in Eq. (9.57),
G(ν
j
)
n
k1
S(y
k
){cos(2πν
j
y
k
)}, (9.71)
has a finite summation range, instead of the infinite large integration range. In
the section on Fourier transformation, we reduced the integration range for the
Fourier transformation of the slit from −∞ to ∞ to a range from −a to a.We
did this because the width of the slit is 2a, and outside the interval from −a to a
there is no information. We may multiply the interferogram function S(y)inthe
integral of Eq. (9.70) with a step function p(y), which is 1 in the interval from
−a to a and otherwise zero. We introduce into Eq. (9.70) the step function p(y),
G(ν)
∞
∫
−∞
p(y)S(y) exp(−i2πνy)dy (9.72)
and reduce the infinite range of integration to a finite range −a to a, which we
may write as
G(ν)
a
∫
−a
S(y) exp(−i2πνy)dy. (9.73)
From the point of view of calculating a Fourier transformation over a limited
range of space, Eq. (9.73) is similar to the discrete Fourier transformation of
Eq. (9.71). In FileFig 9.17 we discuss an example of the Fourier transfor-
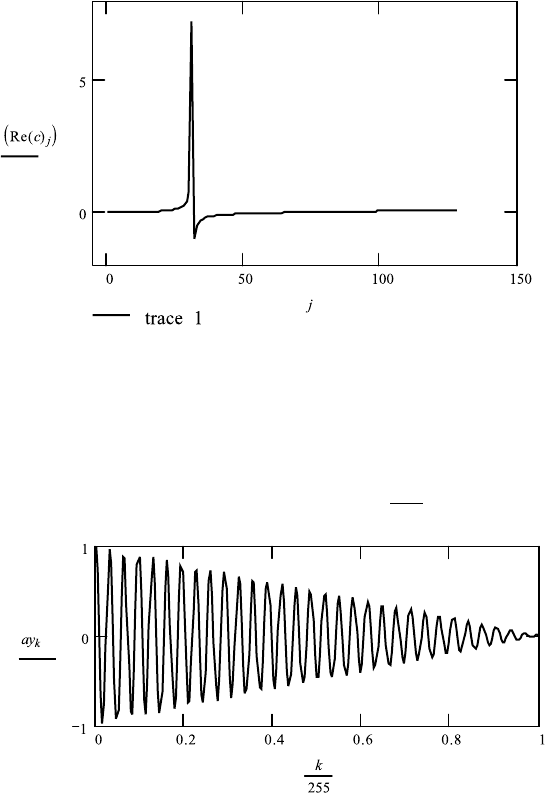
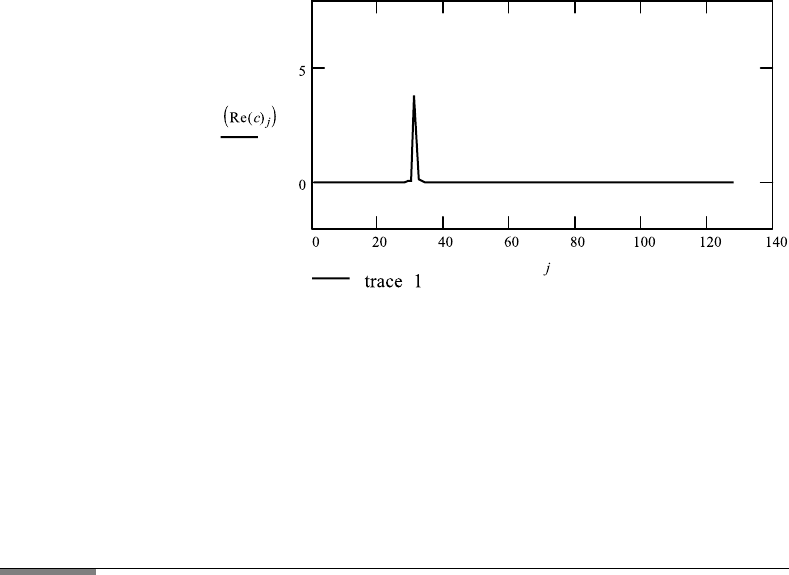
mation of a cos-function integrated over a finite range. We use the function
y
k
cos(2πf k/255), with frequency f 31, plotted over a range of k 0to
400 and do the multiplication with a step function p
k
of width 256 points. The
result of the real Fourier transformation is that we obtain a peak at f 31, not
infinitely narrow and with a loop extending to negative values. Since negative
intensities do not appear in spectroscopy, it is desirable to find a procedure to
avoid this artifact. The situation can be corrected by using in place of p
k
, which
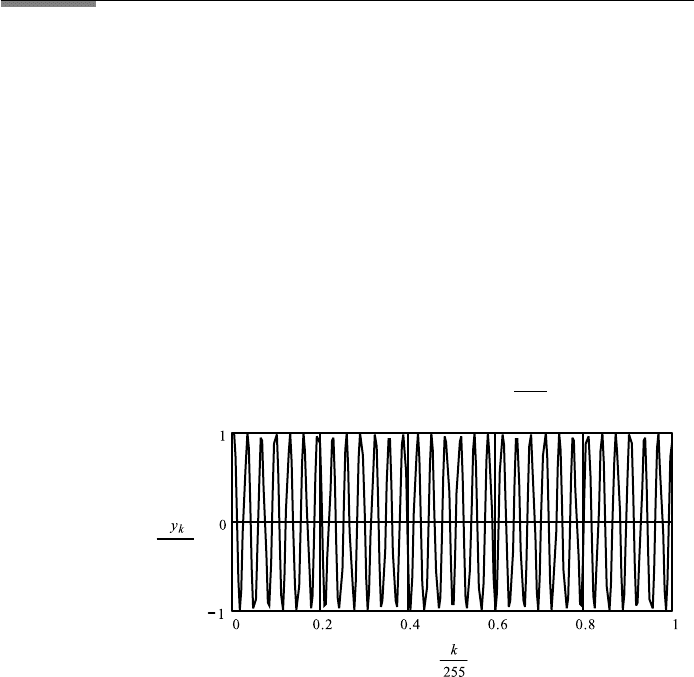
9.2. FOURIER TRANSFORM SPECTROSCOPY 367
is a step function, the function q
k
, which is a triangular function, defined as
q
k
1 − k/255. (9.74)
The multiplication of y
k
by q
k
and their Fourier transformation is shown in
FileFig 9.16. The function y
k
decreases to 0, and remains 0 in the range of
integration, which was set to zero when changing from the infinite range of
integration to the finite range. Application of the Fourier transformation shows
that the negative values of the frequency spectrum have disappeared. This is
called apodization. A drawback to this process is that the resolution is reduced
by a factor of about 2.
FileFig 9.16 (F16APODIS)
Fourier transformation, sin-function, and apodization:
1. the infinite range of integration is reduced to a finite range by the use of a
step function. As a result, the Fourier transformation shows negative intensity
values;
2. the use of the triangular function q
k
1 − k/255 eliminates the negative
values but reduces the resolution by a factor of 2.
F16APODIS
Fourier Transformation of Sine Function and Apodization
1. Original function
k : 0 ...255 y
k
:
cos
2 ·π · f ·
k
255
f ≡ 31.
2. Step function: i : 0 ...400
p
i
: ((i) −(i − (d)) d ≡ 255
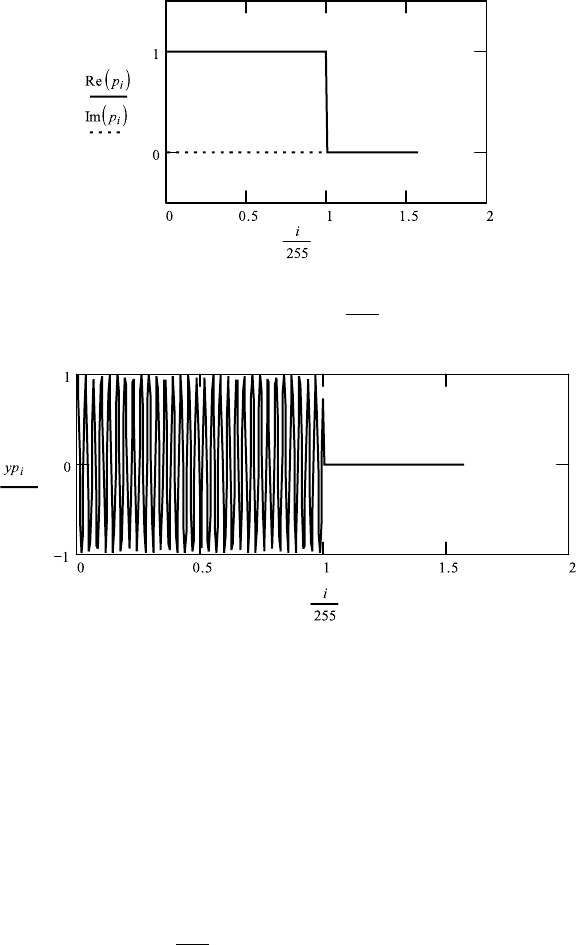
368 9. FOURIER TRANSFORMATION AND FT-SPECTROSCOPY
yp
i
:
cos
2 ·π · f ·
i
255
· p
i
.
3. Fourier transformation of y ×p: we have to use 255 points
x
k
: (cos(2 ·π ·f ·
k
255
)) · ((k) −(k −(d)) k : 0 ...255
c : ff t(x)
N : last (c) N 128
j : 0 ...N.
9.2. FOURIER TRANSFORM SPECTROSCOPY 369
4. Triangle function
ay
k
: q
k
· y
k
q
k
: 1 −
k
255
.
5. Fourier transformation of y ×p; we have to use 255 points
N 128
j : 0 ...N
c : ff t(ay)
N : last (c).
370 9. FOURIER TRANSFORMATION AND FT-SPECTROSCOPY
Application 9.16.
1. Use the apodization function qq
k
(1−k/255)
2
and calculate the apodized
function and the Fourier transform. Compare with the use of p
k
and q
k
.
2. Study the impact of the reduction of resolution. Repeat the procedure for a
sum of five cosine functions of five different frequencies, such as 30, 35, 40, 45,
and 50. Study the resolution using the apodization functions p
k
, q
k
, and qq
k
.
APPENDIX 9.1
A9.1.1 Asymmetric Fourier Transform Spectroscopy
We have discussed the use of the Michelson interferometer for spectroscopy. The
sample was assumed to be positioned either before the light was divided at the
beam splitter or after the light was recombined. The reflection and transmission
properties of the two arms of the interferometer were assumed to be equal and
the only asymmetry was the difference in the path. To calculate the spectrum we
could use the “real" Fourier transformation.
We now assume that the sample is at the surface of one of the mirrors of
the Michelson interferometer. The reflection properties of the two arms of the
interferometer are then different and the complex Fourier transformation must
be applied. As a result of using the complex Fourier transformation one has
more information available (complex numbers instead of real numbers). We
may calculate not only the intensity (square of amplitude) but also obtain phase
information. If in the case of reflection for a certain frequency range, the reflected
amplitude and the phase change at reflection are known, the optical constants n
and K may be calculated. We start with Eqs. (9.34) and (9.35), describing the
two beams reflected from the two mirrors in the Michelson interferometer. We
assume that the light is reflected in the fixed arm by a mirror producing the same
magnitude of the amplitude and a phase shift of π. Using complex notation we
