Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple

Подождите немного. Документ загружается.

9.1. FOURIER TRANSFORMATION 351

We now discuss the case where G(ν) is the product of two functions g

(ν) and

(ν),

G(ν)  g

(ν)g

(ν). (9.17)

In the cases where one wants to keep the two functions separate, one can represent

the Fourier transformation of G(ν) by a convolution integral. The convolution

integral theorem tells us that we may write the Fourier transform of the product

(ν)g

(ν) as the convolution integral of the Fourier transformations of g

(ν)

and g

(ν). The Fourier transformation of g

(ν)is

(y) 

+∞

∫

−∞

(ν)expi2πνydν (9.18)

and of g

(ν)

(y) 

+∞

∫

−∞

(ν)expi2πνydν. (9.19)

The Fourier transform S(y) of the product G(ν)  g

(ν)g

(ν) is calculated from

the convolution integral

S(y) 

∞

∫

−∞

(τ )s

(y −τ)dτ, (9.20)

where s

(y) and s

(y) are the Fourier transforms of g

(ν) and g

(ν) (see

Eqs. (9.18) and (9.19)).

A simple example can be discussed by splitting the Gauss function

G(ν)  exp −(a

)/2 (9.21)

into two, as

exp − (3/4)(a

)/2 (9.22)

exp − (1/4)(a

)/2. (9.23)

We calculate the Fourier transform of Eqs. (9.22) and (9.23) as

(y) 

∞

∫

−∞

{exp −(3/4)(a

)/2}cos 2πνydν (9.24)

and

(y) 

∞

∫

−∞

{exp −(1/4)(a

)/2}cos 2πνydν (9.25)

and using the formula of Eq. (9.6), one gets

(y)  (

√

2π/a

√

3) exp −(8π

)/(3a

) (9.26)

(y)  (

√

2π/a)exp−(8π

)/(a

). (9.27)

352 9. FOURIER TRANSFORMATION AND FT-SPECTROSCOPY

The Fourier transform of G(ν) (i.e., S(y)) is now obtained from the convolution

integral

S(y) 

∞

∫

−∞

(τ )s

(y −τ)dτ (9.28)

S(y)  8π/(

√

3)(a

)

∞

∫

−∞

exp{−(8π

)/(3a

) − (8π

)(y −τ)

}dτ. (9.29)

Using the integral formula

∞

∫

−∞

exp(−t

)dt {

√

π} (9.30)

and introducing a complementary term +(3y/2)

− (3y/2)

in the exponent of

the integral, one may write [2τ − (3y/2)]

and obtain for Eq. (9.29),

S(y)  ({

√

2π}/a) exp(−2π

). (9.31)

If we had calculated the Fourier transformation of G(ν)  exp −(a

)/2, we

would have obtained the same result:

S(y)  (



2π/a) exp(−2π

). (9.32)

In FileFig 9.11 we show the convolution integral for the case where the two

factors are a step and a sin cx function.

FileFig 9.11 (F11CONVOS)

Convolution integral of the step function and the sin x/x function.

F11CONVOS is only on the CD.

Application 9.11. Calculate analytically the integral and show the effect of the

convolution process of the step function on the sin x/x function.

9.2 FOURIER TRANSFORM SPECTROSCOPY

9.2.1 Interferogram and Fourier Transformation.

Superposition of Cosine Waves

We next discuss the superposition of plane waves in order to understand the

formulas of Fourier transform spectroscopy. We consider a plane wave solution

of the scalar wave equation

u(x,t)  A cos 2π(x/λ − t/T + φ). (9.33)

9.2. FOURIER TRANSFORM SPECTROSCOPY 353

In Chapter 2 we discussed the dependence on x and t and on the phase factor φ.

We write the two cosine waves with path difference x

 x

− δ as

(x,t)  A cos 2π(x

/λ − t/T) (9.34)

(x,t)  A cos 2π[(x

− δ)/λ − t/T]. (9.35)

Using the formula

cos α +cos β  2[cos(α + β)/2][cos(α −β)/2], (9.36)

we may write for the superposition u  u

+ u

u  u

+ u

 2A[cos(2π(δ/2)/λ)]{cos[2π (x

/λ − t/T) −2π(δ/2)/λ]} (9.37)

and obtain for the intensity

I {2A[cos(2π(δ/2)/λ)]}

.{cos[2π(x

/λ − t/T) −2π(δ/2)/λ]}

. (9.38)

Only the second factor depends on the time. Since it oscillates very quickly;

we can assume that only the average value is detected and results in a constant.

Therefore we have

I {2A cos(2π(δ/2)/λ)}

(times a constant). (9.39)

We see that the intensity of the superposition of the two harmonic waves depends

only on the optical path difference δ.

9.2.2 Michelson Interferometer and Interferograms

The Michelson interferometer (see Figure 9.1) has been discussed in Chapter 2,

and we assume that an ideal beam splitter reﬂects and transmits 50% of the

incident light. The incident beam is divided at the beam splitter and each beam

is reﬂected at one of the two mirrors M

and M

. Part of the reﬂected beam from

is transmitted, and part of the beam coming from M

is reﬂected. These two

parts are superimposed and travel to the detector.

The optical path difference is introduced by the displacement of the mirror

. If the mirror is displaced by nδ/2, the optical path difference is nδ for each

wavelength component of the incident beam. The center position is at δ  0.

There we have constructed interference for all wavelengths. For constructed

interference in the direction of the detector, for a speciﬁc wavelength no light

travels back to the source. For destructive interference in the direction of the

detector, the light travels back to the source.

Since only the space dependence of the harmonic wave is of importance we

write the amplitude of the input wave as

(x)  A cos 2π(x

/λ). (9.40)

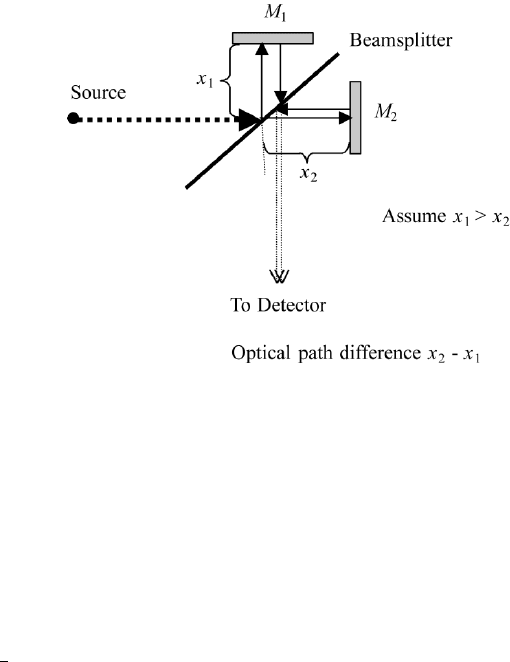
354 9. FOURIER TRANSFORMATION AND FT-SPECTROSCOPY

FIGURE 9.1 Schematic of Michelson interfometer. The optical path difference x

− x

 δ/2is

produced by displacement of mirror M2.

The superposition of the two waves emerging from the beam splitter is (see

Eq. (9.38))

u(δ)  B cos(2π(δ/2)/λ), (9.41)

where B is a constant. For the intensity we obtain

I (δ) {B cos(2π (δ/2)/λ)}

, (9.42)

where B

represents the effective intensity at the detector for δ  0.(Note the

factor

in the argument which comes from δ/2 in Eq. (9.39)).

So far we have assumed for the input wave (Eq. (9.40)) only one wavelength

or one frequency. The case of interest for Fourier transform spectroscopy is the

determination of the frequency spectrum when the incident wave contains many

frequencies. We assume that we have p waves of amplitude A

and (discrete)

wavelength λ

which as frequencies we write as ν

 1/λ

in cm

−1

. The input

of the sum of waves (amplitudes) is

u 



i1

cos(2πν

) (9.43)

and for the intensity of the output at the detector one has

I (y) 



i1

cos(2πν

y/2)}

, (9.44)

where y is the optical path difference produced by the two mirrors. Each of the

incident waves in the sum of Eq. (9.43) will separately produce a superposition

pattern and all intensity patterns will be superimposed (see Eq. (9.44)). We apply

9.2. FOURIER TRANSFORM SPECTROSCOPY 355

to each term the formula

cos

α  (1/2)(1 +cos 2α) (9.45)

and obtain

I (y) 



j1

{1 + cos(2πν

y)}. (9.46)

Note that the factor 1/2 in the argument of Eq. (9.44) has now disappeared.

Although we need a discontinuous representation for the realistic case of Fourier

transform spectroscopy, we use integral presentation for the manipulations to

obtain the interferogram function.

9.2.3 The Fourier Transform Integral

In Fourier transform spectroscopy we observe the intensity pattern at the detector,

depending on a “length" coordinate, and calculate the frequency pattern using

Fourier transformation.

We now consider a continuous frequency distribution from ν  0toν ∞

and write Eq. (9.46) as an integral over dν,

J (y)  2



∞

G(ν){1 + cos(2πνy)}dν, (9.47)

where we have replaced C

by the continuous function G(ν) and the sum by an

integral. For the speciﬁc case of y  0 we get

J (0)  4

∞

∫

G(ν)dν. (9.48)

Fourier integrals need for ν and y the range from −∞ to ∞. We therefore

formally extend the frequency range by assuming that G(ν) is symmetric around

ν  0 and therefore that G(−ν)  G(ν). For Eq. (9.48) we then may write

J (0)  2

∞

∫

−∞

G(ν)dν (9.49)

and write for the cos-function in Eq. (9.47) the corresponding exponential,

including negative frequencies, and get

J (y) 

∞

∫

−∞

G(ν){1 + e

i(2πνy)

}dν. (9.50)

Introduction of Eq. (9.49) into Eq. (9.50) gives us

J (y)  (1/2)J (0) +

∞

∫

−∞

G(ν){e

i(2πνy)

}dν. (9.51)

The function J (y) contains the observed data.

356 9. FOURIER TRANSFORMATION AND FT-SPECTROSCOPY

We deﬁne the interferogram function S(y)as

S(y)  J (y) −(1/2)J (0) 

∞

∫

−∞

G(ν){e

i(2πνy)

}dν. (9.52)

The subtraction of 1/2 J (0) from J (y) produces negative values for S(y) and

makes it a Fourier integral of the type we have discussed above. If a double-

sided interferogram is obtained, y runs from negative to positive values related

to the position of the mirror M

of the Michelson interferometer. Using the

fast Fourier transformation, we can only consider 2

points. The input function

starts with the positive part of S(y) and the negative part follows as a mirror

image. Therefore, the information we are interested in is only contained in the

single-sided interferogram.

The integral S(y) is one of the pair of Fourier transform integrals

S(y) 

∞

∫

−∞

G(ν){e

i(2πνy)

}dν. (9.53)

The other is

G(ν) 

∞

∫

−∞

(S(y){e

−i(2πνy)

}dy. (9.54)

(Note the negative sign in the exponent.) The integral of Eq. (9.54) is the one

we need to calculate the frequency spectrum of the observed data, presented by

S(y).

We have assumed that both variables ν and y have continuous values from

−∞ to +∞. When G(ν) and S(y) are symmetrical with respect to zero, the

imaginary part disappears and one has to deal only with one side of the integral.

The Fourier transformation pairs are then

S(y)  2

∞

∫

G(ν){cos(2πνy)}dν (9.55)

G(ν)  2

∞

∫

(S(y){cos(2πνy)}dy. (9.56)

9.2.4 Discrete Length and Frequency Coordinates

9.2.4.1 Discrete Length Coordinates

The Fourier integral of Eq. (9.56) is the Fourier transformation of the

interferogram function. For numerical calculations it is written as

G(ν

) 



k1

S(y

) cos(2πν

). (9.57)

Since the coordinates ν

and y

each have n discrete values, the Fourier

transformation is equivalent to the solution of a system of n linear equations.

9.2. FOURIER TRANSFORM SPECTROSCOPY 357

The input data of the interferogram function S(y

) are the measured data. The

mirror M

of the Michelson interferometer (Figure 9.1) is moved at equal steps

from one position to the next, and the values of the interferogram are recorded at

the detector.The zero path length position is the location of the central maximum.

The input values of the interferogram function S(y

) are calculated by subtraction

of half the value of the central maximum (Eq. (9.52)).

In the cosine functions of Eq. (9.57) we have a set of values of y

and as a

consequence we have a repetition of possible values of ν

. Let us choose for the

length interval y

 k, which means we have 128 points from k  1 to 128, and

consider

cos[2π(ν

k)]. (9.58)

When k is 128, and ν

is 1/128 we have ν

k  1, which means all values of the

cosine are in one cycle for k  1 to 128 and ν

 1/128. When the product (ν

is larger than 1, we have repetition. Let us assume the value ν

 133/128 

1 + 5/128,

cos[2π(133/128)k]  cos[2π (1 +5/128)k] (9.59)

 cos[2π(5/128)k].

Because of the periodicity of the cos-function, the frequency ν

 133/128

is equivalent to ν

 5/128. When using k  1 to 128 points in the space

coordinate domain, after application of the Fourier transformation, all that we

can get are 128 frequencies in the frequency domain. The repetition at 2π is

shown in FileFig 9.12. In addition, the cos-functions of Eq. (9.57) have “mirror"

symmetry at the center of the interval (at i  64), and at both ends (shown in

FileFig 9.13). In FileFig 9.14 graphs are shown of amplitudes and intensities

of the superposition of cosine waves. These superpositions are simulations of

interferograms depending on the optical path difference.

FileFig 9.12 (F12FTDISC1S)

Graphs are shown of cos(2πν

k) for the space coordinate from 1 to 128

and frequencies 1/128, 2/128, 3/128, 64/128, 127/128, 128/128, 129/128, and

130/128.

F12FTDISC1S is only on the CD.

Application 9.12. Consider a total of n  32 points in the space domain and

show on a graph the ﬁrst ﬁve frequencies. Then ﬁnd the functions that have the

same appearance around frequency numbers 32 and 64.

358 9. FOURIER TRANSFORMATION AND FT-SPECTROSCOPY

FileFig 9.13 (F13FTDISC2S)

Graphs are shown of cos(2πν

k) for the space coordinate from 1 to 128 and

frequencies 1/128, 2/128, 63/128, 64/128, 65/128. A section of k  20 to 80 of

cos(2πν

k) for 63/128, 64/128, and 65/128 shows that the frequency of 63/128

appears similar to 65/128 and both have a larger cycle than 64/128.

F13FTDISC2S is only on the CD.

Application 9.13. Make graphs of cos(2πν

k) for higher and lower frequencies

than 64/128 and show that they appear similar to graphs of lower and higher

frequency numbers.

FileFig 9.14 (F14MICHOPS)

Simulations of interferograms for the Michelson interferometer. Graphs of

amplitudes and intensities of cosine functions depending on optical path

difference.

F14MICHOPS is only on the CD.

9.2.4.2 Sampling

We have seen in FileFig 9.13 that the cos-function of Eq. (9.57) has a symmetrical

appearance around the frequency position 64/128, when using 128 points in

space and having exactly two space points per cycle. For this special example

two points per cycle have been used for the characterization of the frequencies.

In general, we have from information theory the sampling theorem.

Theorem 9.1. Two points per cycle are needed for sampling a continuous

periodic function in order not to lose information.

In our example, the continuous functions are cos-functions. The cos-function

with the highest frequency is sampled by using two points per cycle. For exam-

ple, one is at the maximum and one is at the minimum. Lower frequencies are

also correctly sampled, but higher frequencies present a problem. They appear

as lower frequencies and need to be removed by a ﬁlter. When talking about

wavelengths instead of frequencies, we similarly have that the sampling inter-

val is equal to one-half of the wavelength of the shortest wavelength (highest

frequency). Calling the sampling interval l,wehave

l  1/(2ν

), (9.60)

where ν

is the highest frequency of the spectrum under consideration. In Fourier

transform spectroscopy it is assumed that all higher frequencies are removed.

9.2. FOURIER TRANSFORM SPECTROSCOPY 359

9.2.5 Folding of the Fourier Transform Spectrum

What happens when the choice of the sampling interval is done incorrectly? How

is the spectrum affected? We show that higher frequencies are folded around the

highest frequency, corresponding to the correct sampling interval, and appear

as lower frequencies in the spectrum. We use for the space domain the coor-

dinate points 1/256, 2/256,...,1 and consider the sum of cos-functions with

frequencies 65, 85, and 105.

1. The sampling interval is 1/256. We have

 cos[2π ·65(i/256)] +cos[2π ·85(i/256)]

+ cos[2π105(i/256)], (9.61)

where i runs from 1 to 256.

2. The sampling interval is 2/256. We consider

 cos[2π ·65(2i/256)] + cos[2π ·85(2i/256)]

+ cos[2π105(2i/256)], (9.62)

where i runs from 1 to 256.

3. The sampling interval is 4/256. We have

 cos[2π ·65(4i/256)] +cos[2π ·85(4i/256)]

+ cos[2π · 105(4i/256)], (9.63)

where i runs from 1 to 256.

In FileFig 9.15 we compare the appearance of the spectrum for these three

sampling intervals 1/256, 2/256 and 4/256.

FileFig 9.15 (F15FOLDS)

Folding of the spectrum:

1. Sampling interval 1/256 for the function y1. The three frequencies to be

investigated are 65, 85, and 105. The highest frequency is 128. All frequencies

appear at the right place in the Fourier transformation spectrum.

2. Sampling interval 2/256 for function y2. We now use a sampling interval

twice as large. Consequently the highest frequency is now 64 and the three

frequencies 65, 85, and 105 are all higher than 64. The spectrum appears

folded. In the Fourier transformation the three frequencies appear at 45, 85,

and 125. Since the frequency spectrum is shown over 128 points, we may look

at the function y2 as it would have frequencies 2 ·65, 2 ·85 and 2 ·105 and

is sampled with the sampling interval 1/256 (as we did under (1), where the

highest frequency is 128.) We then have to look for the frequencies 130, 170,

and 210, which all exceed the frequency interval from 1 to 128. We saw in

360 9. FOURIER TRANSFORMATION AND FT-SPECTROSCOPY

FileFigs 9.12 and 13 that higher frequencies are folded back into the spectrum

around the highest frequency (which is 128 because we sample y2 now like

y1). We have to subtract from 130, 170, and 210 the highest frequency 128

and ﬁnd 2, 42, and 82. These values have to be traced back from 128 because

of the folding. We get 126, 86, and 46, which are the frequencies we should

ﬁnd in the graph of the Fourier transformation. However, we ﬁnd 125, 85,

45 because we have not taken into account that the Fourier transformation

program starts at 0 and not at 1.

3. Sampling interval 4/256 for function y4. We now use a sampling interval

4/256 to sample the same function with 4/256. The highest frequency is now

32. In the Fourier transformation the three frequencies appear at 5, 85, and

90. Since the frequency spectrum is shown over 128 points, we look at y4 as

it would have frequencies 4 · 65, 4 · 85, and 4 · 105. It is sampled with the

sampling interval 1/256, as y1 was. We have to look for the frequencies 260,

340, and 420, which all exceed the frequency interval from 1 to 128. We saw in

FileFigs.12 and 13 that higher frequencies are folded back into the spectrum

around the highest frequency (which is 128 because we sample y4 now like

y1). We have to subtract from 260, 340, and 420 the highest frequency 128,

and get 132, 212, and 293. Then we have to trace back from 128, because

they all exceed 128 and get 4, 84, and 165 and have to fold again at 0 into

forward (i.e., 4, 84, and 165). The ﬁrst two are now in the right position, but

165 exceeds 128. We have to subtract 128 from 165 which is 37 and trace it

back from 128, that is, we get to 91. We ﬁnally get for the position of the three

frequencies 4, 84, and 91, and those are the frequencies we should ﬁnd in the

graph of the Fourier transformation. However, we ﬁnd 5, 85, and 90. The ﬁrst

two are folded twice, the last three times. We have not taken into account that

the Fourier transformation program starts at 0 and not at 1.

F15FOLDS

Folding of the Spectrum

For the sampling interval 1/255, hightest frequency is 128; the frequencies are

at 65, and 105, all below 127.

1. Sample interval i/255

i : 0 ...255

: cos



2 ·π · 65 ·

255



+ cos



2 ·π · 85 ·

255



+ cos



2 ·π · 105 ·

255

