Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple

Подождите немного. Документ загружается.

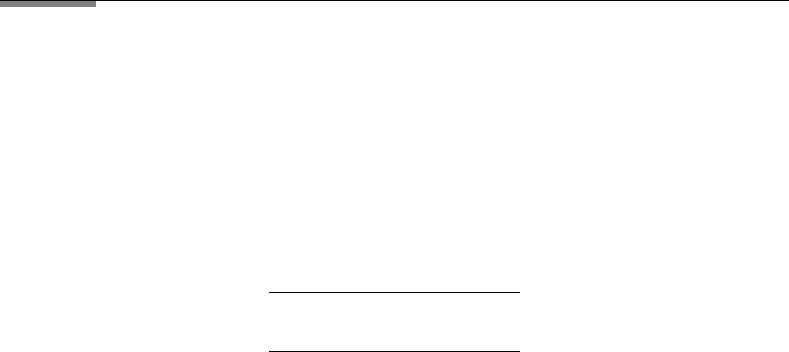
320 8. OPTICAL CONSTANTS

polarized and has an effect on the oscillator under consideration. The local ﬁeld

at the oscillator must be corrected. This is called the Lorentz correction and the

effective ﬁeld at the site of the charges is

E + (1/3ε

)P. (8.24)

Using P  ε

NαE we have

 ε

Nα{E

+ (P

/3ε

)}. (8.25)

Similar to the low density case, using Eq. (8.9), the square of the refractive index

for the denser medium is

 1 + Nα/(1 −(Nα/3)). (8.26)

This equation may also be written as

3(n

− 1)/(n

+ 2)  Nα (8.27)

and is called the Clausius–Mossotti equation, or with the parameters of our

model,

 1 + 3ε

/{3(ω

− ω

− iγω) − ω

}. (8.28)

We have in a solid that the interaction between the oscillators becomes very

strong. The oscillation frequencies are modiﬁed and the damping constants

become large. In addition, in crystals the periodicity must be taken into account.

8.3 DETERMINATION OF OPTICAL CONSTANTS

8.3.1 Fresnel’s Formulas and Reﬂection Coefﬁcients

The determination of the two parts n and K of the complex refractive index may

be accomplished by using reﬂection measurements. In Chapter 5 we found that

Fresnel’s formulas relate the reﬂection coefﬁcients of the p- and s-polarization

cases to the real index of refraction. In a similar way to that of Chapter 5, one can

show that the complex reﬂection coefﬁcients are related to complex refractive

indices through Fresnel’s formulas. Replacing n

by n

∗

 n

−iK

we have for

the reﬂection coefﬁcients

∗





− iK

) cos θ −n

cos θ



− iK

) cos θ +n

cos θ



(8.29)

∗

⊥



cos θ − (n

− iK

) cos θ



cos θ + (n

− iK

) cos θ



. (8.30)

In order to represent r



and r

⊥

depending on the angle of incidence. We need the

law of refraction in complex terms (see FileFig 8.4 (M4SNELL) of Chapter 5).

The law of refraction is

sin θ  (n

− iK

) sin θ



. (8.31)

8.3. DETERMINATION OF OPTICAL CONSTANTS 321

The angle θ



must be a complex quantity since the left side of Eq. (8.31) is real.

Introduction of Eq. (8.31) into Eqs. (8.29) and (8.30) gives us

∗





− iK

) cos θ −n



1 −{(n

sin θ)/(n

− iK

)}

− iK

) cos θ +n



1 −{(n

sin θ)/(n

− iK

)}

(8.32)

∗

⊥



cos θ − (n

− iK

)



1 −{(n

sin θ)/(n

− iK

)}

cos θ + (n

− iK

)



1 −{(n

sin θ)/(n

− iK

)}

. (8.33)

In FileFig 8.1 we have graphs of the absolute value and the argument for re-

ﬂected amplitudes of the parallel (zrp) and perpendicular (zrs) cases depending

on n and K.ForK  0 we see from the ﬁrst graph that for the parallel case

the minimum corresponding to the Brewster angle is not zero. The angle at the

minimum is called the principal angle. The second graph shows the phase jump

at the Brewster angle, which is now a smooth transition. In the application of

FileFig 8.1, Section 3, we plot the parallel (zrp) and perpendicular (zrs) cases

for several different values of n and K on the same graph.

FileFig 8.1 (O1FRNKPSS)

Graphs are shown for reﬂected amplitudes of the parallel (zrp) and perpendic-

ular (zrs) cases depending on n and K for n

 1. For both cases the absolute

value of the reﬂected amplitudes and the phase angle are plotted for n1  1,

n2  1.5, and K  2.

O1FRNKPSS is only on the CD.

Application 8.1.

1. Make a graph and ﬁnd the values of the principal angle for one value of n

and three values of K.

2. Make a graph and ﬁnd the values of the principal angle for one value of K

and three values of n.

3. Observe that the curve of arg(zrp(θ )) is not continuously approaching the

curve of arg(zrs(θ)) when K is going from 0.01 to zero. What is the remaining

phase difference?

8.3.2 Ratios of the Amplitude Reﬂection Coefﬁcients

Equations (8.32) and (8.33) give the dependence of the reﬂection coefﬁcients

on n and K. We have the general problem that we cannot represent n and K as

functions of r

and r

. This is only possible for approximations, (see Appendix

8.1), and other methods have to be considered.

322 8. OPTICAL CONSTANTS

One method is to apply reﬂection measurements at several angles of incidence

to determine the absolute values of the ratio r

. The ratio r

is calculated

similarly to that done by Born and Wolf (1964, p.617).

From Chapter 5 the ratio r

⊥



from Fresnel’s formulas is

⊥



 [(n

cos θ − n

cos θ



)/(n

cos θ + n

cos θ



)]/ (8.34)

[(n

cos θ − n

cos θ



)/(n

cos θ + n

cos θ



)]. (8.35)

Using the law of refraction and the trigonometric formula for the sum of angles

cos(a ± b)  cos a cos b ± sin a sin b (8.36)

we get

| r

|| cos(θ − θ



)/ cos(θ + θ



) | . (8.37)

In FileFig 8.2 we show graphs of the real parts of r

and r

for various values

of n and K. The third graph shows the ratio r

and the fourth r

. From

these two graphs it appears that the ratio r

is much more useful for the

determination of optical constants than the ratios r

, because they are smooth

and do not show a resonance, related to the appearance of the Brewster angle.

The optical constants may be obtained by measuring values of |r

| for two

different angles of θ, and solving the two equations for the unknowns n and K.

FileFig 8.2 (O2FRSOPS)

Graphs are shown for the real part of the ratios r

and r

, calculated with

the expressions used in FileFig 8.1, for n1  1, n2  1.5, nn2  1.5, K  0.1,

and K  0.01, KK  0.5, KKK  2.

O2FRSOPS is only on the CD.

8.3.3 Oscillator Expressions

8.3.3.1 One Oscillator

To ﬁt experimental data of a narrow frequency range, in which we have a reso-

nance feature, one may use for n +iK a similar expression derived in Eq. (8.23)

but extended to four parameters,

n + iK 



A + S/[1 −(ν/ν

)

− γ (ν/ν

)], (8.38)

where A is a general constant, S the oscillator strength, γ the damping constant,

and ν

 ω

/2π the resonance frequency. An example is shown in Figure 8.2

and a calculation given in FileFig 8.3.

8.3. DETERMINATION OF OPTICAL CONSTANTS 323

FIGURE 8.2 Optical constants of bone charcoal powder. Resonance of vibrations of Ca, P , and

O atoms against each other. (From Tomasecli et al., infrared optical constants of black powders

determined from measurements, Applied Optics, 1981, 20, 3961–3967.)

FileFig 8.3 (O3OSTINS)

Graphs are shown of Eq. (8.37) for A  20, S1  0.09, γ 1  0.002, and

1  1050 cm

−1

. An analytical approximation for n close to 1 and small K is

also presented.

O3OSTINS is only on the CD.

Application 8.3.

1. Change γ and observe the change in resonance wavenumber and the height

of the imaginary part.

2. Change S and observe the change in resonance wavenumber and the height

of the imaginary part.

3. Modify the graphs by plotting in addition a graph using S2  0.19, γ 2 

0.03, and ν

2  1150 cm

−1

. Change parameters and study the effect on n

and K.

4. Modify the graphs of the thin medium by also plotting a graph using different

values of a2 and c2. Change a1, a2 and c1 and cc and compare the effect on

n and K.

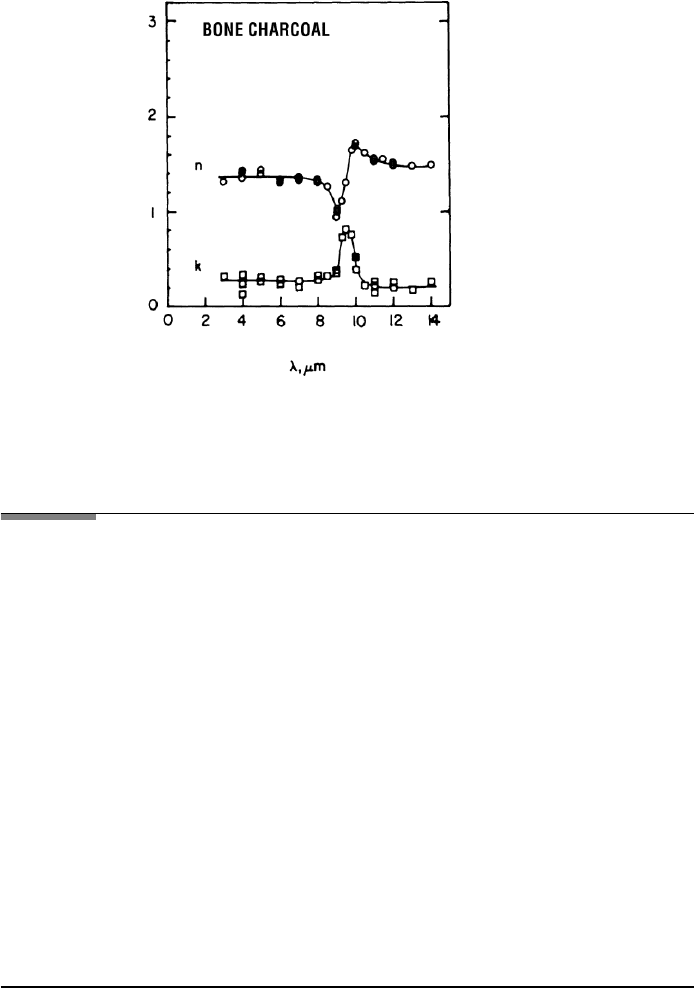
8.3.3.2 Many Oscillator Terms

The dependence of the electrical polarization on the frequency over a large

range suggests that one uses more than one oscillator term in the formula for the

324 8. OPTICAL CONSTANTS

FIGURE 8.3 The dependence of the polarizability on frequency for the microwave, infrared, and

ultraviolet regions.

representation of n and K (schematically shown in Figure 8.3). Having measured

n and K overa largerange of frequencies, the experimental data are ﬁt to formulas

such as

− K

 1 +



(ω

− ω

)/((ω

− ω

)

+ (γjω)

) (8.39)

2nK 



ω/((ω

− ω

)

+ (γjω)

), (8.40)

where f

, γ

, and ω

are empirical constants. The constants in these expressions

are determined by a “best ﬁt" calculation over a large range of frequencies with

respect to the measured values of n and K

8.3.4 Sellmeier Formula

Similarly to what has been discussed for the oscillator expression, one may ﬁt

experimental data to represent the dependence of n and K on the wavelength by

using a polynomial approach of the type

 c

+ c

/(λ

− c

) +

jN



j1

/(λ

− b

). (8.41)

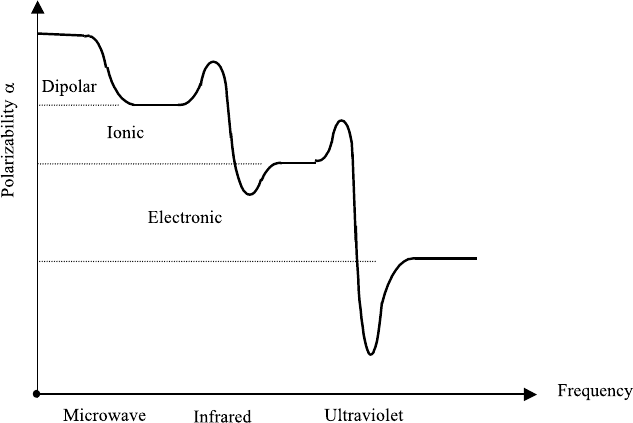
8.3. DETERMINATION OF OPTICAL CONSTANTS 325

This is called a Sellmeier-type equation and has been used, for example, to ﬁt the

data for potassium bromide in the spectral region from .2 to 42 microns using

11 empirical constants.

An example is given in FileFig 8.4.

When ﬁtting experimental data one has to keep in mind that n and K are not

independent. They are related by the Kramer–Kroning model.

In some spec-

tral regions, for example in the x-ray region, one obtains the K value from

absorption measurements and calculates the corresponding n value with the

Kramer–Kroning model.

FileFig 8.4 (O4SELMRS)

A graph of a Sellmeier expression n(λ) for fused quartz is shown for the range

of λ from 4000 to 8000 Angstrom using parameters c

with i  1 to 3.

O4SELMRS

Graph for Demonstration of the Sellmeier Presentation of the Refractive Index

For fused quartz we have

c1: 1.448 c2: 3.3 · 10

c3: 1.23 · 10

λ : 4000, 4001 ...8000

n(λ): c1 +

Application 8.4. Determination (backward) of the constants c1, c2, and c3.

Read from the graph three values of λ

and the corresponding value of n(λ

Consider c1 to c3 as unknown and formulate a system of linear equations. One

E. D. Palik, Handbook of Optical Constants of Solids II, Academic Press, NewYork, 1991.

Charles Kittel, Introduction to Solid State Physics, John Wiley & Sons, New York, 1967.

326 8. OPTICAL CONSTANTS

would be n(λ

)  c1+c2/λ

+c3/λ

. Solve the system of these inhomogeneous

linear equations with one of the available computer programs. Make an estimate

of the error.

8.4 OPTICAL CONSTANTS OF METALS

8.4.1 Drude Model

In Section 8.2 we discussed the optical constants of dielectrics and in Section 8.3

their determination. We now discuss metals and how their optical constants are

also described by a complex refractive index. The determination of the n and

K values for metals is similar to what has been discussed before, but the model

representing the material is different.

Metals show high reﬂectivity in the visible and infrared spectral regions and

their attenuation increases with lower frequencies. The values of real and imag-

inary parts of the refractive index of metals are in the lower frequency region

which is much higher than one usually ﬁnds for dielectrics.

The interaction of the electromagnetic wave with the metal is described by

the Drude model. The electrons are assumed to move almost freely in the metal

and there is no restoring force to make the electrons vibrate, as discussed for

the dielectric. For an isotropic medium with free conducting charges we write

Maxwell’s equations as

∇×E −∂B/∂t

∇×B  ∂E/∂t +j/ε

(8.42)

∇·E  0

∇·B  0.

This is similar to Eq. (8.1). For the current density vector j we take

j  Nev

, (8.43)

where v

is called the drift velocity. The electrical ﬁeld of the light and the

current density in the material are related by the wave equation. We assume E

and j are vibrating in the y direction and propagating in the x direction and from

Eq. (8.41) we get for the wave equation

∂

/∂x

− (1/c

)∂

/∂t

 [1/(c

)]∂j

/∂t. (8.44)

As in Section 8.2, we now ﬁnd an expression for j

in terms of the parameters of

the damped oscillator model and the vibrating electrical ﬁeld E

. The differential

equation of the model is now without the force term,

u/dt

+ mγ du/dt  eE

−iωt

. (8.45)

8.4. OPTICAL CONSTANTS OF METALS 327

The general solution of Eq. (8.44) is the sum of the solutions of the homogeneous

and inhomogeneous equations. For the homogeneous equation,

u/dt

+ mγ du/dt  0. (8.46)

Using the trial solution u  u

−t/τ

, we get for γ  τ

−1

. Typically one has a

value of 10

−13

for τ and we neglect this solution.

The inhomogeneous equation may be rewritten, using v  du/dt,as

mdv/dt + mγ v  eE

−iωt

, (8.47)

Using the trial solution v  v

−iωt

one obtains

 E

(e/m)/(γ − iω). (8.48)

The current density j

 Nev

can be expressed as

 (τE

)(Ne

/m)/(1 −iωτ)  (σE

)/(1 − iωτ), (8.49)

where we used j

 Nev

, γ  τ

−1

, and the static conductivity

σ  τNe

/m. (8.50)

Equation (8.48) relates the current density j

of our model to the electrical ﬁeld

of the light, vibrating with angular frequency ω.

We now turn to the wave equation, (see Eq. (8.43)), using the trial solutions

 E

i(kx−ωt)

and j

 j

i(kx−ωt)

(8.51)

and introducing j

from our model, Eq. (8.48), we obtain for the complex wave

vector k

∗

)

 1/c

{ω

+ (iσω/ε

)/(1 − iωτ)} (8.52)

and the complex refractive index n

∗

 k

∗

/ω

∗

)

 1 + iσ/{ωε

(1 − iωτ)}1 − σ/{ωε

(i +ωτ)}. (8.53)

Equation (8.52) relates the refractive index to the static conductivity of the metal

σ , the frequency of light ω and the relaxation time τ , which is a parameter of

our model and is related to the metal. In FileFig 8.5 we show graphs over a large

frequency region of the real and imaginary parts of Eq. (8.52).

8.4.2 Low Frequency Region

For low frequencies, that is, when ωτ  1, we may neglect ωτ with respect to

i (see Eq. (8.52)), and get

∗

)

 1 + iσ/ωε

. (8.54)

Since ω is small, which means iσ/ωε

is large compared to 1, we write

n − iK  (

√

i)(



σ/ωε

). (8.55)

328 8. OPTICAL CONSTANTS

Using the identity

√

i  (1 +i)/

√

2 one has

| n || K | (



σ/2ωε

); (8.56)

that is, n and K have the same value and the wave is strongly attenuated in

the medium. To ﬁnd the frequency limit of Eq. (8.55), we have from ωτ  1,

that ω<<1/τ , with τ  mσ/N e

. For copper we have σ  5.76 10

(ohm

meter)

−1

, N  8.510

meter

−3

, e  1.610

−19

coulomb, m  9.11 10

−31

kgm,

and obtain for 1/τ  4.110

1/sec. Therefore this approximation is valid for

angular frequencies smaller than 10

− 10

Hz, which are lower frequencies

than the far infrared. This approximation is plotted in FileFig 8.5 as the last graph.

The light is strongly attenuated when entering metals in this spectral region and

is therefore highly reﬂected (see also FileFig 8.7).

8.4.3 High Frequency Region

For high frequencies we have ωτ  1, and from Eq. (8.52) one has

 1 − σ/ω

τε

. (8.57)

Using Eq. (8.49) and the plasma frequency ω

 Ne

/mε

we have

 1 − ω

/ω

. (8.58)

The plasma frequency ω

 Ne

/mε

has the value 1.6 10

1/sec when using

N  8.510

meter

−3

, e  1.610

−19

coulomb, ε

 8.85 10

−12

farad-meter

−1

and m  9.11 10

−31

kg. Therefore the approximation of Eq. (8.57) is valid for

angular frequencies larger than 10

, corresponding to the x ray region. This is

also plotted in FileFig 8.5 on the third graph. In this region the refractive index n

is real and less than 1 and light is penetrating the metal without being attenuated.

We see that the plasma frequency divides the frequency range into two parts.

One for high frequencies when n is smaller than 1 and one for low frequencies

when n is complex (see Eq. (8.53)).

FileFig 8.5 (O5METALS)

Graphs of the real and imaginary part of n

∗

 n +iK of copper, for the general

case and for the high and low frequency approximations.

O5METALS

Calculation of n and k for Copper Using the Drude Model

Calculation of real and imaginary parts. Expression for low and high frequencies

depending on angular frequency.

8.4. OPTICAL CONSTANTS OF METALS 329

1. General Expression

c : 3 · 10

m/s σ : 6 · 10

(OHMm)

−1

εo : 8.85 · 10

−12

/Nm

τ :

4.1 · 10

sec i :

√

−1

ω : 10

, (2 · 10)

...10

Angular frequency for 1 mm wavelength is 2π

∗

300

∗

∧

9; see below. The

general expression for n − ik  zm(ω)

zm(ω):

1 +



i ·σ

εo · ω



1 − i ·ω · τ

. . . . . . . .

. .