Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple
Подождите немного. Документ загружается.

7.6. CONFOCAL CAVITY, GAUSSIAN BEAM, AND MODES 299
where z
R
is a constant. We express the function q(z) as a combination of the
radius of curvature of the wavefront R(z) and the beam waist w(z)
2
as
1/q(z) 1/(iz
R
+ z) 1/R(z) − iλ/(πw(z)
2
) (7.73)
and determine R(z) and w(z)
2
from Eq. (7.72) and (7.73), after separation of
real and imaginary parts, we have
w(z)
2
(λ/π){z
R
+ z
2
/z
R
} (7.74)
and
R(z) z + z
2
R
/z. (7.75)
The function w(z)
2
is the beam waist, which is the width of the beam depending
on z (Figure 7.16). R(z) is the curvature of the wavefront of the beam depending
on z (Figure 7.17).
7.6.2 Fundamental Mode in Confocal Cavity
The confocal cavity was discussed in the chapter on geometrical optics. It is a
stable cavity with radii of curvature of the mirrors equal to the length d of the
cavity. The fundamental mode of the solution of the paraxial wave equation (see
Eq. (7.68)), is the same for rectangular mirrors of a cavity for which Cartesian
coordinates are used and for circular mirrors for which cylindrical coordinates
are used.
We show that the radius of curvature of the wavefront of the Gaussian beam
in the confocal cavity matches the curvature of the mirrors at distance z d/2
and −d/2, counting z from the middle at 0.
7.6.2.1 Beam Waist
The beam waist is indicated in Figure 7.16. Inserting Eq. (7.73), into Eq (7.69)
and taking the real part one has (exp −kr
2
λ/2πw(z)
2
). With q kλ/2π and
setting q 1 for simplicity we get (exp −r
2
/w(z)
2
). This factor decreases in
the transversal direction and is 1 for r 0 and 1/e for r w(z). The beam is
attenuated from its value at r 0 at the axis to 1/e at distance r from the axis.
7.6.2.2 Wavefront of Beam at Center and at Mirror
Wavefront at Center
The wavefront is plain when R(z) ∞. If we choose this value at z 0, one
gets from Eq. (7.73)
1/q(0) −iλ/(πw(0)
2
) (7.76)
From Eq (7.74) we have for the total waist in the middle w
2
0
w(0)
2
(λ/π)z
R
.

300 7. BLACKBODY RADIATION, ATOMIC EMISSION, AND LASERS
Wavefront at Mirrors
For z z
R
we have
R(z z
R
) 2z
R
and w(z z
R
)
2
(λ/π)
2
z
R
2w
2
0
. (7.77)
We choose 2z
R
d equal to the distance d between the two mirrors, which is
also the radius of curvature of the spherical mirrors in the confocal cavity. The
radius of curvature of the wavefront at z d/2 matches the radius of curvature
of the mirrors.
Confocal Cavity
For the confocal cavity the radius of curvature of the wavefront, when approach-
ing the mirror, is equal to the radius of curvature of the mirror (see Figure 7.17).
The beam waist is 2w
2
0
at the point z d/2, which is twice as large as at its
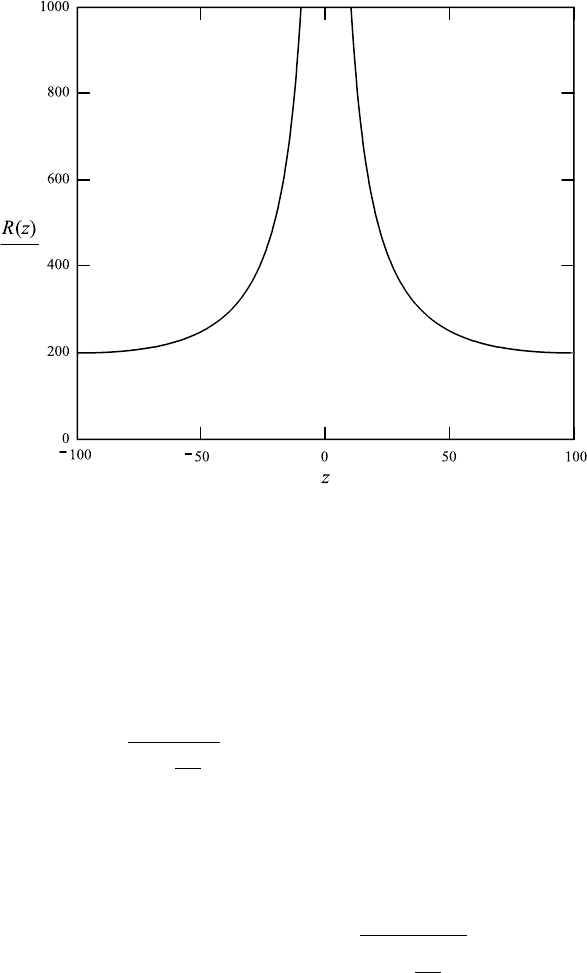
minimum at z 0. In FileFig 7.10 we have plotted w(z) and R(z) over the range
z −100 to 100, which is the distance between the mirrors equal to the length
d 2z
R
200. One observes the beam waist at z 0 and one obtains for the
radius of the wavefront at z 100, that is, R(100), the value 200, corresponding
to the radius of curvature of the mirror R
m
d.
The half angle of the opening of the beam in the far field approximation is the
angle θ
ap
of the asymptote of w(z), which passes through z 0. It is obtained
as
lim
z→∞
w(z)/z w
0
/z
R
λ/πw
0
. (7.78)
The asymptote y zw
0
/z
R
is also indicated in FileFig 7.10.
FileFig 7.10 (L10WRS)
Graphs are shown for the radius of the wavefront R(z), beam waist w(z), and
the asymptote y(z).
L10WRS
Radius of Curvature and Beam Waist
1. Radius of curvature
Beam waist is normalized to 1; that is, we plot (w(z) w0SQR(1+(z/zR)
2
)
and set w0 .1 in cm, and zR π(ω0)2/λ − .01π/λ, λ in cm. Radius of
curvature R(z) z + (zR)
2
/z
R(z):
z +
zR
2
z
zR : 100
z :−100, −99.99 ...100.
7.6. CONFOCAL CAVITY, GAUSSIAN BEAM, AND MODES 301
Rm 2zR.Atz 1/2 of distance of mirrors, that is, for distance 200 at
100, the radius of curvature must be equal to the distance of the mirrors.
2. Beam waist
Plots of two branches of the beam waist and the asymptote to w(z); that is,
y z/zR.
If z is in cm, we have set for w0 .1, λ 3.14
∗
0.01/zR in cm (about 3
microns for zR 100).
w(z): .1 ·
"
1 + (
z
zR
)
2
and for the asymptote yy(z):−y(z),
ww(z):−.1 ·
%
1 +
z
zR
2
.

302
7. BLACKBODY RADIATION, ATOMIC EMISSION, AND LASERS
Application 7.10.
1. Repeat the calculations for λ 10 microns, z
R
100 cm.
2. Repeat the calculations for λ 3 microns, z
R
160 cm.
3. Repeat the calculations for λ 10 microns, z
R
160 cm.
7.6.3 Diffraction Losses and Fresnel Number
The diffraction losses of a mirror of diameter 2a at distance d are characterized
by the Fresnel number F . We assume parallel light incident on an obstacle of
diameter 2a and have for the diffraction angle θ λ/2a (see Figure 7.18). The
geometrical shadow AG at distance d is 4a
2
π and the total area AT, enlarged by
diffraction, is 4(a + θd)
2
π. The Fresnel number is defined as F AG/(AT −
AG), which is
F 4a
2
π/{(4a
2
+ 8ad(λ/2a) + ...)π −4a
2
π}
4a
2
π/(8adλπ/2a) a
2
/dλ, (7.79)
where a term in θ
2
was neglected in the denominator.
FIGURE 7.18 Diffraction angle for mirror. The geometrical shadow has the area AG. The total
area of the light is AT . The Fresnel number is defined as F (AG)/(AT − AG).
7.6. CONFOCAL CAVITY, GAUSSIAN BEAM, AND MODES 303
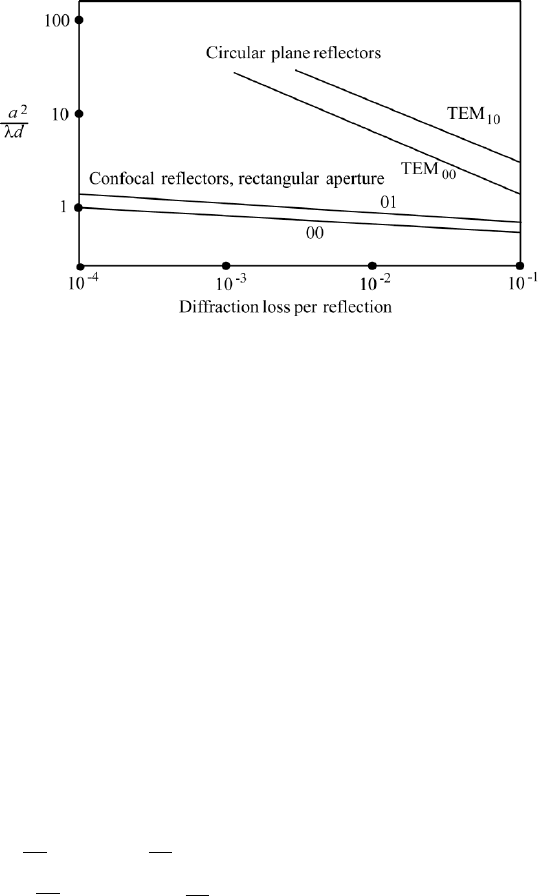
FIGURE 7.19 Fresnel numbers for circular plain reflectors and confocal reflectors. The confocal
cavity is about two orders of magnitude better than a Fabry–Perot cavity.
A confocal resonator has considerably fewer losses for Fresnel numbers larger
than 1 compared to Fabry–Perot resonators. For example, at F 1 the confocal
resonator does more than 300 times better than the Fabry–Perot (Figure 7.19).
7.6.4 Higher Modes in the Confocal Cavity
We have discussed in Section 7.2 the fundamental mode in a confocal cavity. The
fundamental mode is the same for a cavity using rectangular mirrors or spherical
mirrors. The higher modes need for their description Cartesian coordinates for
rectangular mirrors and cylindical coordinates for round mirrors. In both cases
we have TEM modes characterized by three mode numbers, the first two for the
transversal modes and the last for the longitudinal modes.
7.6.4.1 Confocal Cavity and Rectangular-Shaped Mirrors (Cartesian Coordinates)
Forthe higher modes of cavitieswith rectangular-shapedmirrors, using Cartesian
coordinates (x,y,z), the solution of the paraxial wave equation (see Eq. (7.68)),
is
ψ H
m
(
√
2x/w) ·H
n
(
2y/w) ·exp{−i(P (z) + k(x
2
+ y
2
)/2q(z))}, (7.80)
where H
m
(
√
2x/w) and H
n
(
√
2y/w) are Hermitian polynomials, each a solution
of a differential equation written in the variable u as
d
2
H
m
/δu
2
− 2u · dH
m
/du + 2mH
m
0. (7.81)
The indices m and n are the transverse mode numbers. The Hermitian
polynomials for m equals 0 to 3 are
H
0
(u) 1
H
1
(u) u (7.82)

304 7. BLACKBODY RADIATION, ATOMIC EMISSION, AND LASERS
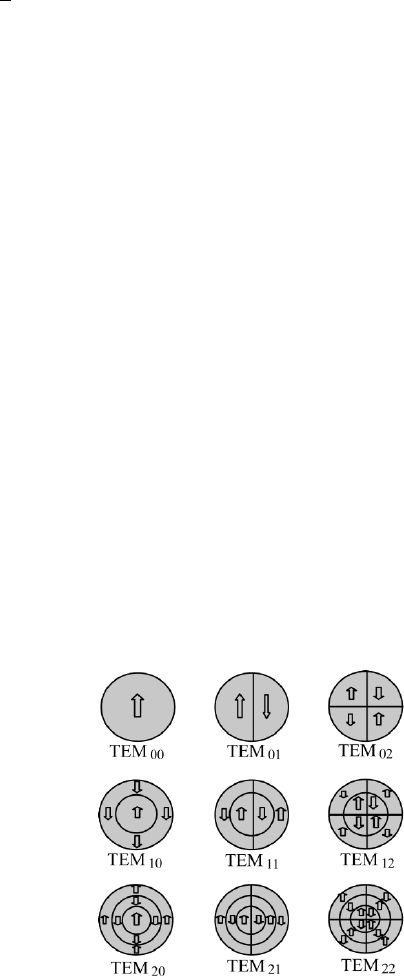
FIGURE 7.20 Schematic of modes for a cavity with rectangular mirrors.
H
2
(u) 4u
2
− 2
H
3
(u) 8u
3
− 12u.
The fundamental mode, discussed above, has the indices m 0 and n 0.
The higher modes are labeled by TEM
mnq
, where n and m refer to the Hermi-
tian polynomials (Eqs. (7.81) and (7.82)). They are transversal mode numbers
and correspond to the number of vertical or horizontal zero-intensity lines in the
transversal pattern. A schematic representation is given in Figure 7.20. The lon-
gitudinal mode is characterized by the large number q. Since the phase has to be
the same after one round trip, one obtains the following resonance condition,
2L/λ
nmq
1/2(m + n + 1) + q. (7.83)
There are degenerate modes if m + n + 2q m
∗
+ n
∗
+ 2q
∗
. For the mode
separation one has v
00 q+1
−ν
00q
c
/2L, where c
is the phase velocity in the
medium of the cavity and is independent of the Fresnel number.
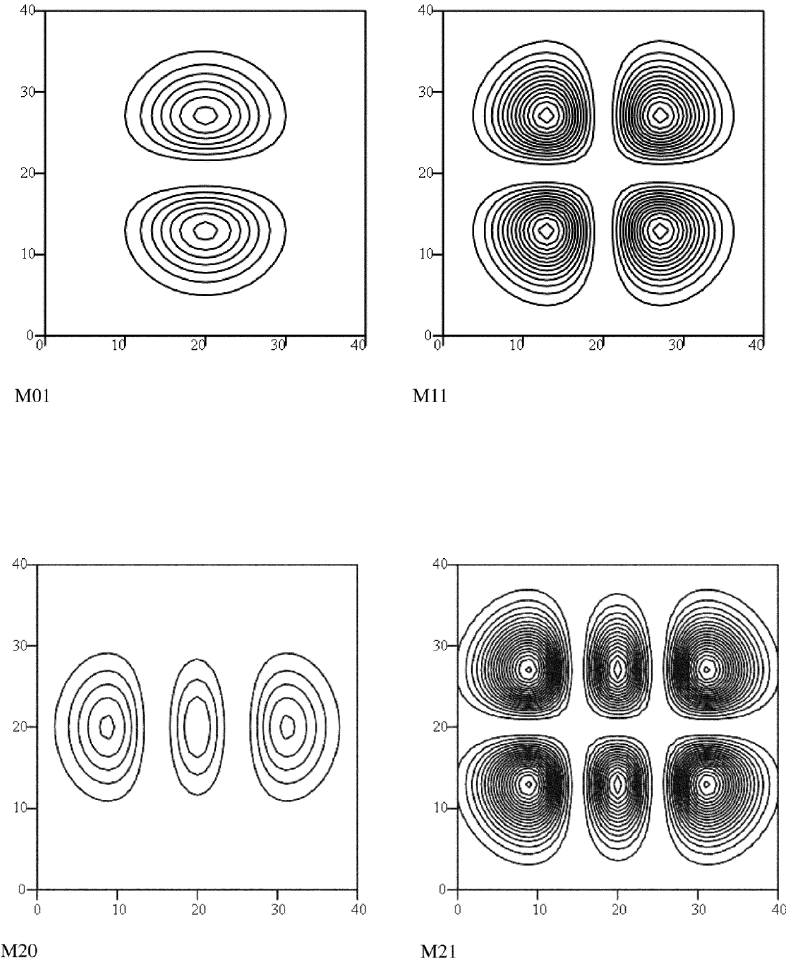
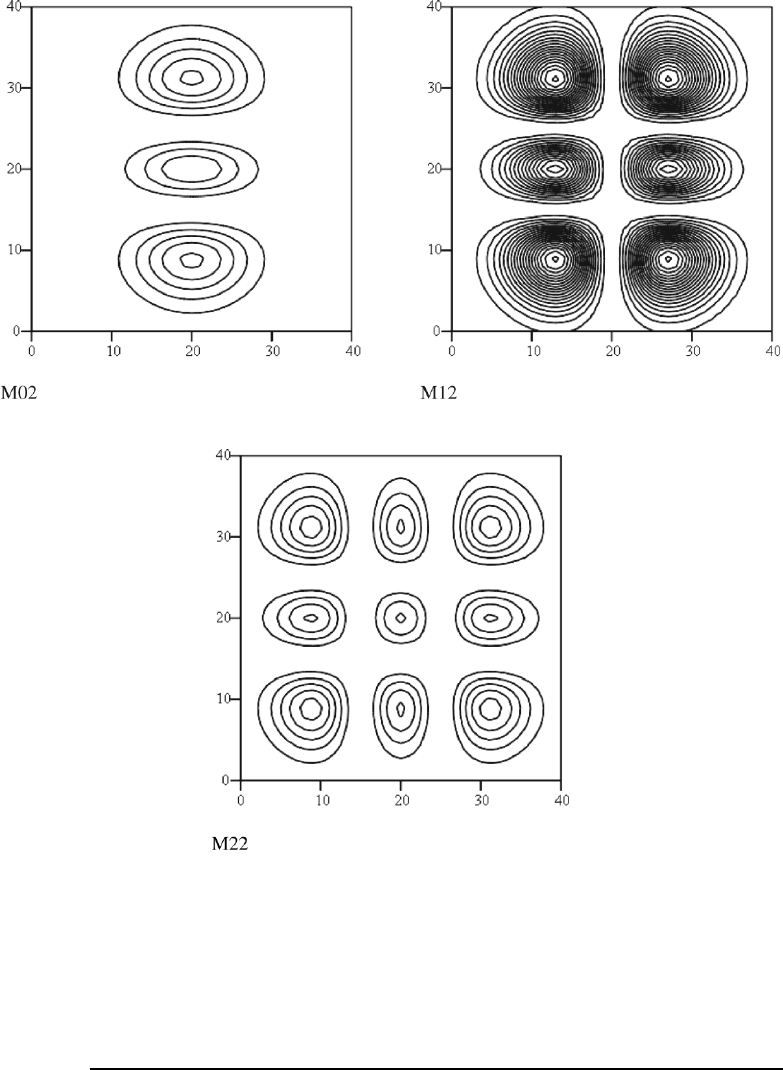
In FileFig 7.11 we show surface graphs of the higher-order modes in the
transversal direction from (0,0) to (2,2).
FileFig 7.11 (L11MOCONFCS)
Modes for confocal cavity and rectangular mirrors. Surface plots of Hermitian
polynomials with exponential factor for indices 0, 1, and 2, and scaling factors
X and Y .
L11MOCONFCS
Cartesian Coordinates for Rectangular Mirrors in the Confocal Resonator
Field distribution as contour plot. The mode numbers m and n are for hermi-
tian polynomials. The constant in the exponential is simulated by X. Small X

7.6. CONFOCAL CAVITY, GAUSSIAN BEAM, AND MODES 305
corresponds to small waist width.
N : 40 i : 0 ...N j : 0 ...N
x
i
: (−20) + 1.00 · iy
j
: (−20) + 1.00 · j
H 0(x): 1 H 0(y): 1 H 1(x): x ·
"
2
Y
H 1(y): y ·
"
2
Y
H 2(y): 4 ·
"
2
Y
· y
2
− 2 H 2(x): 4 ·
"
2
Y
· x
2
− 2
H 00(x,y): H 0(x) · H 0(y)
H 20(x,y): H 2(x) · H 0(y)
H 02(x,y): H 0(x) · H 2(y)
H 01(x,y): H 0(x) · H 1(y)
H 11(x,y): H 1(x) · H 1(y)
H 10(x,y): H 1(x) · H 0(y)
H 21(x,y): H 2(x) · H 1(y)
H
12(x,y): H 1(x) · H 2(y)
R(x, y): (x)
2
+ ((y))
2
.
Constant X:
X ≡ 100 Y ≡ 100 g(x,y):
e
−R(x,y)
X
.
M00
i,j
:
g(x
i
,y
j
) · H 00(x
i
,y
j
)
2
M10
i,j
:
g(x
i
,y
j
) · H 10(x
i
,y
j
)
2
306 7. BLACKBODY RADIATION, ATOMIC EMISSION, AND LASERS
M01
i,j
:
g(x
i
,y
j
) · H 01(x
i
,y
j
)
2
M11
i,j
:
g(x
i
,y
j
) · H 11(x
i
,y
j
)
2
M20
i,j
:
g(x
i
,y
j
) · H 20(x
i
,y
j
)
2
M21
i,j
:
g(x
i
,y
j
) · H 21(x
i
,y
j
)
2
7.6. CONFOCAL CAVITY, GAUSSIAN BEAM, AND MODES 307
M02
i,j
:
g(x
i
,y
j
) · H 02(x
i
,y
j
)
2
M12
i,j
:
g(x
i
,y
j
) · H 12(x
i
,y
j
)
2
M22
i,j
:
g(x
i
,y
j
) · H 22(x
i
,y
j
)
2
Application 7.11.
1. Compare with Figure 7.20 and the number of zero-intensity lines with the
mode numbers.
2. Extend the modes using H 3(x) and H 3(y) and complete all graphs up to
indices 0, 1, 2, and 3.
3. Convert surface to contour plots.
308
7. BLACKBODY RADIATION, ATOMIC EMISSION, AND LASERS
7.6.4.2 Confocal Cavity and Circular Mirrors (Cylindrical Coordinates)
For circular mirrors, one uses cylindrical coordinates (r, φ, z). After rewriting
the wave equation in these coordinates, one has the solutions
ψ (
√
2r/w)
l
· L
l
p
(2r
2
/w
2
) · exp{−i(P (z) + kr
2
/2q(z))}, (7.84)
where Lp
l
(2r
2
/w
2
) is a generalized Laguerre polynomial. The L
l
p
(2r
2
/w
2
) are
solutions of the differential equation written in the variable u,
ud
2
L
l
p
/du
2
+ (l + 1 − u)dL
l
p
/du + pL
l
p
0. (7.85)
The index p is the radial mode number and l the angular mode number. For
p 0 to 2 we have for the polynomials
L
l
0
(u) 1 (7.86)
L
l
1
(u) l +1 − u
L
l
2
(u) (1/2)(l +1)(l + 2) −(l + 2)u + (1/2)(u
2
). (7.87)
The fundamental mode has the numbers l 0 and p 0. The modes in
confocal cavities with round mirrors are labeled by TEM
lpq
, where l is the
angular mode number corresponding to the number of angular zero-intensity
lines in the transversal pattern (see the schematic presentation in Fig-
ure 7.21). The radial mode number correspond to the number of zero-intensity
rings. The longitudinal mode is characterized by the large number q. The reso-
nance condition, which is the condition that the phase is the same after one round
trip, is
2L/(λ
lpq
(1/2)(l + 2p + 1) +q. (7.88)
There are degenerate modes if l+2p+2q l
∗
+2p
∗
+2q
∗
. The mode separation
is again independent of the Fresnel number and one has again ν
00 q+1
− ν
00q
c
/2L.
FIGURE 7.21 Schematic of modes for a cavity with round mirrors.
