Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple

Подождите немного. Документ загружается.

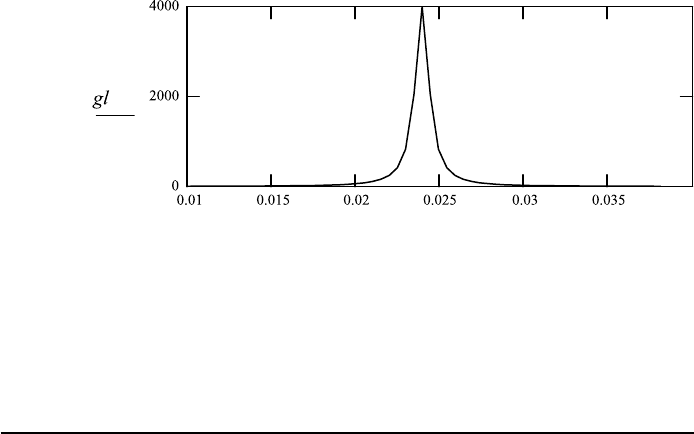
7.4. BANDWIDTH 289

(w)

Application 7.6.

1. For the Lorentzian line shape, change the lifetime τ to more realistic values

in the range of 10

−3

to 10

−8

and ﬁnd a corresponding frequency range.

2. Change the lifetime and ﬁnd the bandwidth. Calculate Q as ω

/ω and

compare with the data from a graph.

7.4.3 Natural Emission Line Width, Quantum Mechanical

Model

In Section 7.4.2 we saw how the width of the Lorentzian line shape depends

on the lifetime τ of the electron in the upper state. The uncertainty principle of

quantum mechanics relates the lifetime τ to the width E of the corresponding

energy state, in which the electron is placed. The uncertainty principle may be

expressed as

Eτ  h/2π. (7.34)

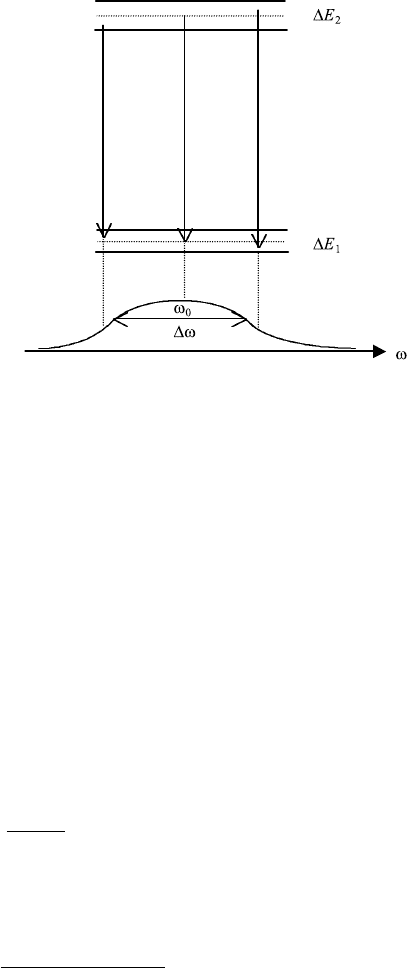
In Figure 7.12 we indicate three possible transitions from the higher to the lower

state. One corresponds to the transition from center-to-center of the two bands,

and the others to the transition between two different energies of the bands,

corresponding to lower and higher frequencies. Quantum mechanics shows that

the center-to-center transition has a higher transition probability than the other

possible transitions. The shape of the emission line shows these differences.

The Einstein coefﬁcient of spontaneous emission A

describes a transition

probability, and is related to the lifetime of the emission process as

 1/τ. (7.35)

7.4.4 Doppler Broadening (Inhomogeneous)

The classical Doppler effect may be observed when a train passes with a blowing

horn. The signal seems to have a higher frequency when the train is traveling

towards us and a lower frequency when traveling away from us. The atoms in a

290 7. BLACKBODY RADIATION, ATOMIC EMISSION, AND LASERS

FIGURE 7.12 The upper energy level has the width E

, the lower E

. Transitions of higher

and lower frequencies are indicated, with respect to the peak frequency of the Lorentzian line

shape.

gas also move while emitting light. The frequency shift, related to their particular

velocity v,isgivenas

ν −ν

 ν

(v/c). (7.36)

The distribution of the velocities depends on the temperature and follows

Maxwell’s velocity distribution law. One gets

I (ν)  I

νo

exp(−E

/kT )  I

νo

exp(−mv

/2kT )

 I

νo

exp{(−mc

/2kT )((ν − ν

)

/(ν

)

)}, (7.37)

where I

is a constant, m the mass of the oscillator, c the speed of light, k the

Boltzmann constant, and T the absolute temperature. As we did in Section 7.4.2

for the Lorentzian line shape, we deﬁne the Doppler line shape as I (ν)  I

gd(ν)

and get

gd(ν)  [(



π(ln 2)(2/π ν)] exp{−(ν − ν

)

(ln 2)/(ν/2)

}. (7.38)

The line shape of Eq. (7.38) has a Gaussian proﬁle which is different from the

Lorentzian, schematically shown in Figure 7.13a.

The halfwidth at half height is calculated to be

ν  2ν



[(2kT /mc

)(ln 2)]. (7.39)

The Gaussian line shape may be looked at as the envelope of a large number

of Lorentzian line shapes. Each oscillator moves with a different velocity in a

different direction and the peak frequencies of the emitted light have a Gauss

distribution, (shown in schematically Figure 7.13b). When discussing an exam-

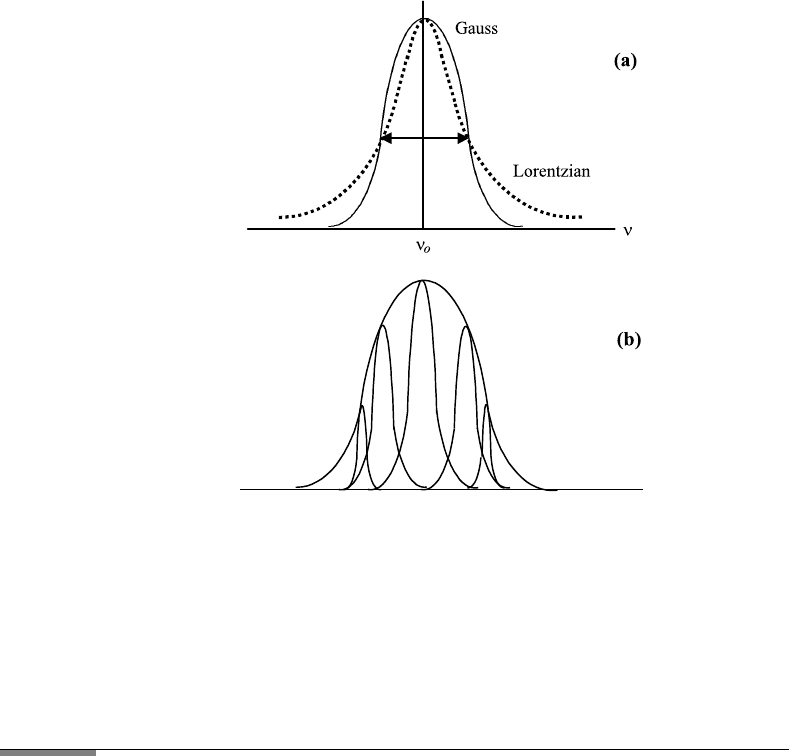
7.5. LASERS 291

∆ν

FIGURE 7.13 (a) Comparison of Lorentzian and Gaussian line shapes of approximately same

line width at half height; (b) Gaussian line shape is the envelope of Lorentzian line shapes emitted

statistically at different velocities in different directions.

ple of the Ne–He laser below, we give numerical values for the halfwidth of

Eq. (7.39).

7.5 LASERS

7.5.1 Introduction

We discussed blackbody radiation in Section 7.2, atomic emission in Section 7.3,

the Fabry–Perot in Chapter 2, and modes in Chapter 6. We now discuss the

following simpliﬁed model for a two-level laser. We consider a Fabry–Perot

ﬁlled with an active medium of atomic oscillators. First we need population

inversion. The oscillators will be excited into the upper state 2 by using the light

of frequency ν

from the outside.We need the excited states to remain excited for

sometime, for example, 10

−3

sec. Then we need stimulated emission to transfer

the energy of the excited oscillators to the modes of the Fabry–Perot. To have

laser light emitted from the Fabry–Perot, one must couple out part of the light

of the modes. This is done by making one of the mirrors of the Fabry–Perot not

totally reﬂective, such as when there is a small hole in the mirror.

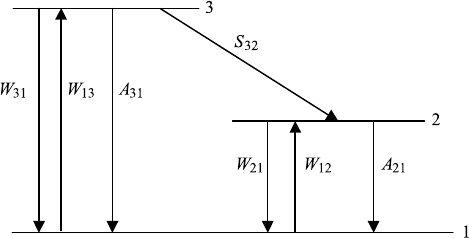
292 7. BLACKBODY RADIATION, ATOMIC EMISSION, AND LASERS

FIGURE 7.14 Schematic of a three-level laser. S

is the probability of a radiationless transition,

and W

are probabilities of induced absorption and emission, and A

is the probability of

spontaneous emission.

7.5.2 Population Inversion

7.5.2.1 Two-Level System with Stimulated and Spontaneous Transitions

When discussing the blackbody radiation law, we used for the occupation of

the different energy levels in thermal equilibrium the Boltzmann distribution

−E/kT

, where k is Boltzmann’s constant. This distribution law tells us that,

at temperature T , the lower states are more occupied than the higher states. For

laser action we need just the reverse, which is more electrons in a higher energy

state. This is called population inversion and is in contrast to the population of

the electrons in thermal equilibrium.

We assume that we have to deal with oscillators having just two levels, as

shown in Figure 7.14. We call the upper level E

and the lower level E

. The

change in time of the number of photons N

of E

and N

of E

, the rate

equations, is

/dt −N

u(ν) + N

(7.40)

/dt +N

u(ν) − N

, (7.41)

where u(ν) is the radiation density. The coefﬁcient B

is the Einstein coefﬁ-

cient of stimulated absorption. The coefﬁcient B

is the Einstein coefﬁcient of

stimulated emission and A

is the coefﬁcient of spontaneous emission. We have

used these coefﬁcients when deriving Planck’s radiation law, (see Section 7.2),

and used the relation

 8πh(ν/c)

(7.42)

as well as B

 B

. This relation has to be slightly changed for atomic os-

cillators. We have to take into account that the atomic energy levels may be

degenerate, which means there are several energy levels having the same energy.

For example, if there is a threefold degeneracy, we have to use the weight g  3

7.5. LASERS 293

for the transition. Therefore we have to use

 g

. (7.43)

7.5.2.2 Changes in the Upper Level Considering Stimulated Transitions

A necessary condition for laser action is population inversion which as stated

before, means there must be more photons in the upper state than in the lower

state. Using only the stimulated emission and absorption processes, we have for

the number of photons in the upperstate.

u(ν), (7.44)

and the number in the lowerstate

u(ν). (7.45)

The change in the number of photons in time is then

/dt  N

u(ν) − N

u(ν). (7.46)

With Eq. (7.43) we write

/dt  [N

− N

)]B

u(ν). (7.47)

To have laser action one needs

− N

> 0 (7.48)

and one has the condition for laser action, N

7.5.3 Stimulated Emission, Spontaneous Emission, and the

Ampliﬁcation Factor

To have the condition N

fulﬁlled, one has to make the stimulated

emission largerthan the spontaneous emission. The stimulated emission transfers

the photons from the upper energy state E

into the modes of the Fabry–Perot.

The bandwidth for the emission process was discussed above and we assume

that we have a Lorentzian line shape. The modes of the Fabry–Perot are much

narrower and close to delta functions (see Figure 7.15). The probability of stim-

ulated emissions per unit time is calculated by considering Eq. (7.46), written

for a number of n photons as

dn/dt  [N

− (g

u(ν). (7.49)

The radiation density is u(ν)  hνn. Taking into account the line shape of

the emission process, (see Eq. (7.30)), we have to multiply the coefﬁcient of

stimulated emission B

by u(ν)gl(ν), that is, B

u(ν)gl(ν), and get

du(ν)/dt  [N

− (g

]hνgl(ν)B

u(ν). (7.50)

294 7. BLACKBODY RADIATION, ATOMIC EMISSION, AND LASERS

−1

FIGURE 7.15 The width of the modes of the cavity at frequencies ν

−1

, ν

, and ν

are almost delta

functions compared to the bandwidth of the Lorentzian-shaped emission line.

We can express the change of u(ν) with respect to the time dt by considering

the length dz in which the light travels in the time dt This gives us dt  dz/c



Here we use the speed of light c



, modiﬁed in the medium of the laser cavity.

The change of the radiation density over the interval dz is then

du(ν)/dz  [N

− (g

](hν/c



)gl(ν)B

u(ν, z). (7.51)

Using A

 1/τ, and A

 8πh(ν/c



)

,wehave

du(ν)/dz {(c



/8πν

τ )[N

− (g

]gl(ν)}u(ν, z). (7.52)

The expression in the curly braces is called the ampliﬁcation factor ε(ν):

ε(ν) {(c



/8πν

τ )[N

− (g

]gl(ν)}. (7.53)

The gain of the beam ε(ν) is “per length” and an example for the Ruby laser is

calculated in FileFig 7.7.

FileFig 7.7 (L7RUBYS)

Gain calculation for the example of the Ruby laser. (See also Kneub

’uhl and

Sigmst, 1988.)

L7RUBYS is only on the CD.

7.5.4 The Fabry–Perot Cavity, Losses, and Threshold

Condition

The Fabry–Perot cavity has two plane parallel mirrors with reﬂectivities R

and

, and the modes are standing waves. These standing waves may be considered

as two traveling waves, moving in opposite directions. If R

and R

have high

reﬂectivity, the traveling waves will pass forward and backward through the

volume ﬁlled with the oscillators in the excited state E

. By stimulated emission,

7.5. LASERS 295

energy will be picked up and the intensity of each mode will increase. This

process will come to an end when the increase in energy is set off by the losses.

Large distances between the two mirrors of the Fabry–Perot correspond to a high

order of longitudinal modes and these high-order modes correspond to a very

narrow bandwidth, schematically shown in Figure 7.15. The intensity depending

on the length z of the light traveling in the active medium of the Fabry–Perot is

related to the radiation density as I (z)  c



u(ν, z). From Eq. (7.50) and (7.51)

we have

dI(z)/dz  ε(ν)I (ν, z). (7.54)

Integration gives us

I (z)  I (0)e

ε(ν)z

. (7.55)

We see the exponential increase of the light traversing the active medium; energy

is transferred to the modes of the Fabry–Perot.

In order to use some of the energy one has to couple it out of the cavity. This

may be achieved by using a mirror with a small hole for one of the two mirrors

of the Fabry–Perot. The length of one round trip is z  2L and the losses are

taken into account by the factor (α(ν)) in the exponent of Eq. (7.55). We multiply

Eq. (7.55) with the reﬂectivities R

to account for the reﬂection losses of one

round trip and get

I (2z)  I (0)e

[ε(ν)−α(ν)]2L

). (7.56)

The thereshold condition is then obtained from Eq. (7.56) when

[ε(ν)−α(ν)]2L

 1 (7.57)

or [ε(ν) − α(ν)]  (1/2L)ln(1/R

). The threshold gain is

(ν)  α(ν) + (1/2L)ln(1/R

) (7.58)

We rewrite Eq. (7.58) by calling σ  [N

− N

)] and insert ε

(ν)in

Eq. (7.53) and get

 [α(ν) + (1/2L)ln(1/R

)](8πν

τ/c



)(1/gl(ν)). (7.59)

This is the famous threshold condition by Schawlow and Townes (Kneub

’uhl

and Sigrist, 1988, p.38). In FileFig 7.8 we present a calculation with numerical

values for the He–Ne laser.

FileFig 7.8 (L8HENES)

Gain calculations for the example of the Ne–He laser. We have used for m in

the mass of the proton times 20 for Ne. The Lorentzian line width has been

296 7. BLACKBODY RADIATION, ATOMIC EMISSION, AND LASERS

replaced by the Doppler line width. The line shape gd(ν) is approximately 1

divided by (2ν



(2kT /mc

)ln2)(see Eq. (7.39).)

L8HENES is only on the CD.

7.5.5 Simpliﬁed Example of a Three-Level Laser

We consider an energy schematic of the oscillators shown in Figure 7.14 with an

upper state 3, a lower state 2, and the ground state 1. We have for transitions be-

tween 3 and 1 induced absorption, induced emission, and spontaneous emission,

as discussed in Section 7.5.2. The transition probabilities are called W

, W

and A

, respectively. A similar description holds for the transitions from 2 to

1. The transitions from 3 to 2 are now special. They are radiationless transitions

and their probability is called S

. The occupation number of the oscillators in

the states 1, 2, and 3 are called N

, N

and the total number N

is assumed

to be a constant.

 N

+ N

. (7.60)

The change in time of the number of oscillators in state 3 is

/dt  W

− (W

+ A

+ S

(7.61)

and in state 2

/dt  W

− (W

+ A

+ S

. (7.62)

For the steady state, the time derivatives are zero. We assume that A

 W

which gives us for the ratio N

of the oscillators

{(W

)/(W

+ S

) + W

}/(A

+ W

). (7.63)

From the discussion of blackbody radiation, W

 W

and W

 W

, and

we assume that the radiationless transition probability S

is much larger than

the transition probability W

(the probability to empty, state 3). We then have

from Eq. (7.63)

{(W

+ W

)/(A

+ W

)}. (7.64)

Using Eqs. (7.60) as N

and (7.61) to (7.63) we may get after some

calculations

− N

)/N

{(W

− A

)/(W

+ A

+ 2W

)}. (7.65)

The threshold condition for operation is obtained when, in the steady state, there

are as many oscillators in state 1 as in state 2, N

 N

. From Eq. (7.65)

one has W

 A

. The minimum power for operation is calculated from the

condition that the power corresponding to induced absorption of level 3 is equal

to the power corresponding to the spontaneous emission of state 2. In FileFig

7.9 we calculate P  NA

hν for a process involving a metastable state and

spontaneous emission.

7.6. CONFOCAL CAVITY, GAUSSIAN BEAM, AND MODES

297

FileFig 7.9 (L9MINPOWS)

Model calculation of minimum power for operation of a laser, P  NA

hν:

1. for a metastable state, and

2. for spontaneous emission.

L9MINPOWS is only on the CD.

Application 7.9. How would the numbers change if S

must be taken into

account?

Take S

 10W

or S

 1000W

7.6 CONFOCAL CAVITY, GAUSSIAN BEAM, AND

MODES

7.6.1 Paraxial Wave Equation and Beam Parameters

Laser light travels forwards and backwards between the two mirrors of a res-

onance cavity. The ﬁrst Ne–He laser used a Fabry–Perot cavity of a length of

one meter between the two plane parallel mirrors and was extremely difﬁcult to

align. Later it was found that the confocal cavity was much easier to align, and

was also very efﬁcient from the point of view of diffraction losses. In Chapter

1, we discussed several types of resonators from the perspective of geometrical

optics, and in Chapter 2 the Fabry–Perot as a resonance interferometer.

In this section we discuss the confocal cavity with radii of curvature R

 d,

where d is the distance between the two mirrors placed at z ±d/2. Here the

origin of the coordinate system is at z  0 in the middle between the mirrors. The

laser beam in the cavity is approximated by a wave traveling in the z direction

and having a bell-shaped proﬁle in the transversal (x, y) direction (Fig-

ure 7.16). For the mathematical presentation of these propagating modes, we

use Cartesian coordinates and rectangular mirrors. We follow H. Kogelnick and

FIGURE 7.16 Waist of a Gaussian beam in a confocal cavity depending on the z coordinate.

298 7. BLACKBODY RADIATION, ATOMIC EMISSION, AND LASERS

FIGURE 7.17 (a) Coordinates for discussion of the radius of curvature of the wavefront of a mode

in a confocal cavity; (b) radius of curvature of the wavefront is indicated for different values of

the z coordinate.

T. Li and start with the scalar wave equation

u/δx

+ δ

u/δy

+ δ

u/δz

+ k

u  0, (7.66)

where k  2π/λ and try to ﬁnd a solution of the wave equation of the form

u  ψ(x,y,z) exp(−ikz). (7.67)

Inserting Eq. (7.67) into Eq. (7.66) and assuming for the calculation that the

second derivative δ

ψ/δz

may be neglected, we further consider the paraxial

wave equation

ψ/δx

+ δ

ψ/δy

− 2ikδψ/δz  0. (7.68)

Solutions of Eq. (7.68) describe a Gaussian beam proﬁle in the transverse

direction, depending on the distance r from the axis, where r

 x

+ y

(Figure 7.17). A solution of Eq. (7.68) is

ψ  exp{−i[P (z) +k(x

+ y

)/2q(z)]} (7.69)

with

δq(z)/δz  1 (7.70)

and

δP(z)/δz −i/q(z), (7.71)

where the two functions q(z) and P (z) are not independent of each other. We are

mainly interested in the solution for q(z) and can solve for P (z) if we need it,

which is a phase factor.

We write the solution of Eq. (7.70) as

q(z)  iz

+ z, (7.72)