Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple

Подождите немного. Документ загружается.

6.3. GUIDED WAVES BY TOTAL INTERNAL REFLECTION THROUGH A PLANAR WAVEGUIDE 259

In FileFig 6.5a we calculate the reﬂected intensity R symbolically and in

FileFig 6.5b we calculate it numerically. One ﬁnds values close to 1 for N  10,

20, 40 or more. Such multiple layer mirrors, consisting of a large number of thin

ﬁlms of alternating high and low refractive indices, are used in laser cavities to

reduce losses.

FileFig 6.5a (N5STRASYMa)

Symbolic calculation of the reﬂected intensity for multilayer reﬂection coatings.

FileFig 6.5b (N5STRANUMb)

Numerical calculation for nH  2.5, nL  1.5, and N  20.

N5STRASYMa and N5STRASYMb are only on the CD.

Application 6.7. Calculate the reﬂected intensity (R) and transmitted intensity

(T  1 − R) for N  10, 20, 40, 100 for chosen values of n

and n

6.3 GUIDED WAVES BY TOTAL INTERNAL

REFLECTION THROUGH A PLANAR WAVEGUIDE

6.3.1 Traveling Waves

When laser light was applied to telecommunication, one looked at the possi-

bilities of light traveling through some type of guide. Travel through the open

air resulted in too many losses. Long wavelength electromagnetic waves travel

through metal cables, but microwaves may travel inside a rectangular waveguide.

These waveguides have parallel reﬂecting metal surfaces, and the wavelength of

a traveling mode is characterized by the dimensions of the rectangular cross-

section. As the ﬁrst step for propagation of modes of laser light one considered a

dielectric ﬁlm of refractive index n

with refractive indices n

and n

equal to 1

on the outside. Later, dielectric ﬁbers were used for guiding the light, discussed

in the next section.

In Chapter 2 we discussed the modes of a Fabry–Perot. The incident light wave

was traveling perpendicular to the planes, and a relation between the wavelength

and the distance between the planes characterized the modes. We now look at

very similar modes, formed inside a plane parallel dielectric ﬁlm but traveling

parallel to the boundaries of the plate.

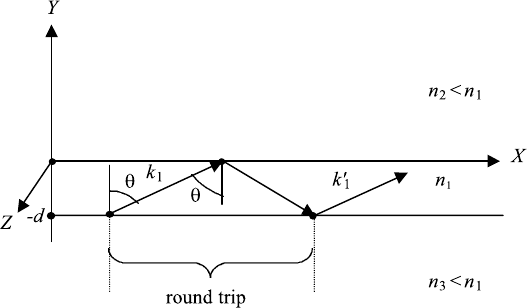
260 6. MAXWELL II. MODES AND MODE PROPAGATION

FIGURE 6.3 Thin ﬁlm of refractive index n

larger than the indices n

and n

of the outside media.

Propagation is in the X direction and mode formation in the Y direction. There are exponential

decreasing solutions in the outside medial of indices n

and n

We consider three layers of dielectric materials extending in the X to Z direc-

tion and stacked up in the Y direction. We assume that the layer in the middle has

thickness d and refractive index n

. Above and below are two other dielectric

materials with refractive indices n

and n

, both smaller than n

(Figure 6.3). A

wave in the layer with refractive index n

is totally reﬂected on the two interfaces,

above and below, and travels effectively in the X direction.

When treating the plane parallel plate (see Chapter 2) we summed up all

the light reﬂected and transmitted at the different interfaces and found resonance

conditions corresponding to modes. Summing up all the reﬂected and transmitted

light is called the summation method in contrast to the boundary value method,

used in Section 6.2 to describe the modes for multilayer dielectric material. To

treat the problem of waves traveling with internal total reﬂection in a dielectric

layer, we apply another method, the traveling wave method. For comparison, the

boundary value method is given in the appendix.

We assume a wave is traveling in the X direction in medium (1) between the

two media 2 and 3. We assume that the angle to the normal θ is larger than the

critical angle, in order to have total reﬂection. A ray is launched from a point

inside the plate and after reﬂection on each interface, the pattern repeats. If the

component of the wave traveling in the Y direction has the same wave vector

after one period of travel in the X direction, we have a traveling mode. This is

only possible for discrete values of the angle θ, the angle corresponding to the

direction of the k vector and the normal (Figure 6.3). We use complex notation

for presenting the wave traveling between internal reﬂections in the X, Y plane

 e

i(2πXn

/λ)

i(2πYn

/λ)

−iωt

, (6.36)

where λ is the wavelength in free space, ω the frequency, t the time, and n

the

refractive index in medium (1). Equation (6.36) is a function of X and Y and

6.3. GUIDED WAVES BY TOTAL INTERNAL REFLECTION THROUGH A PLANAR WAVEGUIDE 261

satisﬁes the scalar wave equation depending on X, Y , and t.We rewrite Eq. (6.36)

using the wave vector notation

 e

i(k

Y )

−iωt

, (6.37)

and have for the components of the wave vectors (k

)

+ (k

)

 k

, with

 n

k and k  2π/λ.

As we know from our discussion of total internal reﬂection, there is an ex-

tension of the internally reﬂected wave into the optically denser medium, called

the evanescent wave. To describe these waves for the two media with refractive

indices n

and n

, we write for the wave in (1), similarly to what we wrote for

the wave in medium (2),

 e

i(k

Y )

−iωt

, (6.38)

with (k

)

+ (k

)

 k

, k

 n

k, and k  2π/λ, and similarly for medium

(3)

 e

i(k

Y )

−iωt

(6.39)

with (k

)

+ (k

)

 k

 n

k, and k  2π/λ.

6.3.2 Restrictive Conditions for Mode Propagation

We recall that we derived a restriction on certain parameters when discussing

the modes in the Fabry–Perot. For the traveling mode in a waveguide we have a

similar, but more complicated situation. The k vectors of the three waves have a

real value for the Y component in medium (1) and an imaginary value in media

(2) and (3) because of total reﬂection. We have for the k vectors:

1. Components of the k vector in the Y direction,

real, and

and

imaginary; and (6.40)

2. Components of the k vector in the X direction

For the three waves traveling in the X direction, the X component of the k

vector has the same real value. We use the notation

 k

 β. (6.41)

The value of β is restricted to k

≥ β ≥ k

and k

≥ β ≥ k

, which follows

from the relations

− β

 k

, but since

is imaginary, β must be larger than k

− β

 k

, but since k

is real, β must be smaller than k

− β

 k

, but since

is imaginary,β must be larger than k

262 6. MAXWELL II. MODES AND MODE PROPAGATION

6.3.3 Phase Condition for Mode Formation

We deﬁne the phase change upon reﬂection on medium 2, (1 → 2), as 

1,2

and

for reﬂection on medium 3, (1 → 3), as 

1,3

. Considering a round trip in the

Y direction, we have for the phase shift: on medium 2: (2πd/λ

)

1,2

, and on

medium 3: 2πd/λ

+

1,3

. The sum must have values of 2πm which is written

2πm  2[2πd/λ

] + 

1,2

+ 

1,3

with m  0, 1, 2, 3. (6.42)

This is the resonance condition for the mode, involving the k values in the Y

direction. The phase values are calculated from Fresnel’s formulas depending

on the Y components of k. The resonance conditions are different for the s-

polarization (TE) modes and the p-polarization (TM) modes, and are discussed

separately in Sections 6.3.4 and 6.3.5.

6.3.4 (TE) Modes or s-Polarization

The reﬂection coefﬁcienton the interfaces 1,2 and 1,3 are obtained from Fresnel’s

formulas (see Chapter 5),



cos θ − n

cos θ



cos θ + n

cos θ



. (6.43)

We multiply by 2π/λ and introduce the deﬁnitions of the k vectors. Since the

values of k in media 1 and media 3 are imaginary, we write

and

and get

complex numbers for the two reﬂection coefﬁcients

˜r

s1,2

 (k

−

)/(k

) (6.44)

˜r

s1,3

 (k

−

)/(k

). (6.45)

For the phase angle we have



s1,2

 tan

−1

(−

) − tan

−1

(

) −2 tan

−1

(

) (6.46)



s1,3

−2 tan

−1

(

). (6.47)

The resonance condition (Eq. (6.42)) may now be written as

d −2 tan

−1

(

) − 2 tan

−1

(

) + πm, (6.48)

or using the formula tan

−1

A + tan

−1

B  tan

−1

(A + B)/(1 − AB) we may

write

tan k

d  [k

(

)]/(k

−

). (6.49)

For the numerical calculation we prefer to write the condition of Eq. (6.49) as

2πn

cos θd/λ −atan





sin

θ − n

]/(n

cos θ )



(6.50)

− atan





sin

θ − n

]/(n

cos θ )



+ mπ, m  1, 2, 3.

6.3. GUIDED WAVES BY TOTAL INTERNAL REFLECTION THROUGH A PLANAR WAVEGUIDE 263

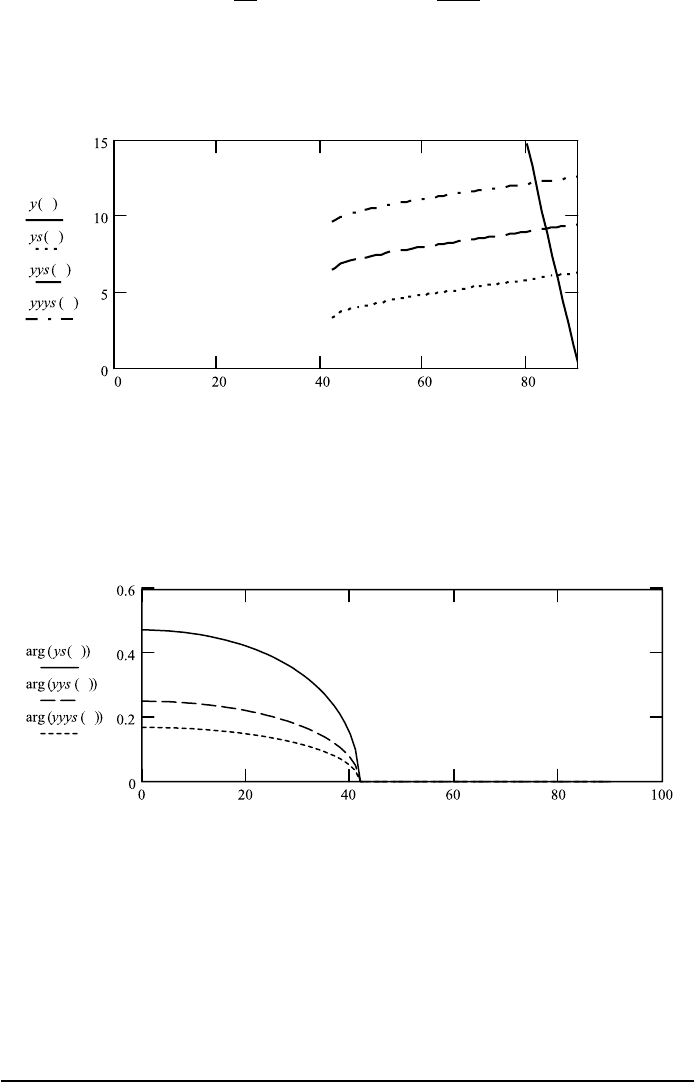
In FileFig 6.6 we calculate the condition of Eq. (6.50) using

ys(θ)  ys2(θ) − ys3(θ) + mπ for m  1

yys(θ )  ys2(θ ) − ys3(θ) +mπ for m  2

yyys(θ )  ys2(θ ) − ys3(θ) +mπ for m  3

and at the crossover point of the graph the resonance condition is fulﬁlled. The

crossover point indicates the angle θ for the mode with mode number m. The

characterization of the mode depends on the refractive indices, thickness d, and

wavelength λ.

FileFig 6.6 (N6PLSPS)

Resonance condition for s-polarization (TE). The crossover point indicates the

angle θ of the mode with mode number m depending on the refraction indices,

thickness d, and wavelength λ. The lowest number of the mode corresponds to

the lowest curve.

N6PLSPS

Wave Traveling with Total Internal Reﬂection Through a Planar Waveguide

Resonance condition of s-polarization. Global deﬁnition of n1, n2, n3, d, and λ

above the graph.

θ : 0, 1 ...90

y(θ): 2 · π ·n1 ·

· cos



2 ·π

360



ys1(θ):−atan(zs1(θ)) zs1(θ):





· sin



2 ·π

360



− n2



n1 · cos



2 ·π

360



ys3(θ):−atan(zs3(θ)) zs3(θ):





· sin



2 ·π

360



− n3



n1 · cos



2 ·π

360



ys is for m  1, yys for m  2, and yyys for m  3. For these parameters the

angle θ of the ﬁrst three possible modes is determined:

ys(θ):−ys1(θ) − ys3(θ) + π

yys(θ ):−ys1(θ) −ys3(θ ) +π · 2

yyys(θ ):−ys1(θ) −ys3(θ ) +π · 3.

264 6. MAXWELL II. MODES AND MODE PROPAGATION

θc : asin





θθc : 360 ·

θc

2 ·π

θθc  41.81

Global deﬁnition

n1 ≡ 1.5 n2 ≡ 1 n3 ≡ 1 d ≡ 18 λ ≡ 2.

At the crossover point of y with ys, yys,oryyys, respectively, the resonance

condition is fulﬁlled. The functions ys, yys, and yyys are complex in the region

from horizontal appearance to zero. This is shown in the next graph where the ar-

gument is plotted.The complex region has to be disregarded for the determination

of the crossover point.

Application 6.6.

1. Change the refractive index and choose d and λ such that all three modes are

possible.

2. Change the thickness d and choose n

and λ such that all three modes are

possible.

3. Change the wavelength λ and choose the refractive index n

and the thickness

d such that all three modes are possible.

6.3. GUIDED WAVES BY TOTAL INTERNAL REFLECTION THROUGH A PLANAR WAVEGUIDE 265

6.3.5 (TM) Modes or

p-Polarization

The coefﬁcients of reﬂection on media 1 and 3 are obtained from Fresnel’s

formulas. First multiply by 2π/λ and then introduce the deﬁnition of k. One

can observe that the k value in the medium above and below is imaginary. One

obtains complex numbers for the two reﬂection coefﬁcients similarly as for the

s-case

˜r

p1,2

 (n

− n

)/(n

+ n

) (6.51)

˜r

p1,3

 (n

− n

)/(n

+ n

) (6.52)

and also for the phase changes



s1,2

 tan

−1

(−n

) − tan

−1

Y )

−2 tan

−1

) (6.53)

and



s1,3

−2 tan

−1

). (6.54)

The resonance condition, similar to Eq. (6.42), may now be written as

d −2 tan

−1

) − 2 tan

−1

) + πm (6.55)

tan k

d  (n

+ n

))/(n

− n

k2Y

). (6.56)

For the numerical calculation we prefer to write the condition as

2πn

cos θd/λ −atan





sin

θ − n

]/(n

cos θ )



(6.57)

− atan





sin

θ − n

)/(n

cos θ )



+ πm,m  1, 2, 3.

In FileFig 6.7 we calculate the resonance condition of Eq. (6.57) using

yp(θ)  yp2(θ) − yp3(θ ) +mπ for m  1

yyp(θ)  yp2(θ) − yp3(θ) + mπ for m  2

yyyp(θ)  yp2(θ) − yp3(θ) + mπ for m  3

and at the crossover point of the graph the resonance condition is fulﬁlled. The

crossover point indicates the angle θ for the mode with mode number m, depend-

ing on the refraction indices, thickness d, and wavelength λ.Givenm, d, and λ,

the k vector for the traveling mode is given and if real, the mode is possible.

266 6. MAXWELL II. MODES AND MODE PROPAGATION

FileFig 6.7 (N7PLPPS)

Resonance condition for p-polarization (TM). The crossover point indicates the

angle θ of the mode with mode number m, depending on the refraction indices,

the thickness d, and wavelength λ. The lowest number of the mode corresponds

to the lowest curve.

N7PLPPS is only on the CD.

Application 6.7.

1. Change the refractive index and choose d and λ such that all three modes are

possible.

2. Change the thickness d and choose n1 and λ such that all three modes are

possible.

3. Change the wavelength λ and choose the refractive index n1 and the thickness

d such that all three modes are possible

4. Give an example for λ  0.00025 mm, d  0.0005 mm and show that we

have for m  1 a cosine mode, and for m  2 a sine mode.

6.4 FIBER OPTICS WAVEGUIDES

6.4.1 Modes in a Dielectric Waveguide

In Section 6.3 we discussed mode propagation in a dielectric ﬁlm of thickness of

several wavelengths and refractiveindex n

.The modes were guided by twoouter

dielectric media of refractive indices smaller than n

. The mode propagation was

in the X direction. The media were stacked in the Y direction and extended in

the Z direction without limits. A constant refractive index was assumed.

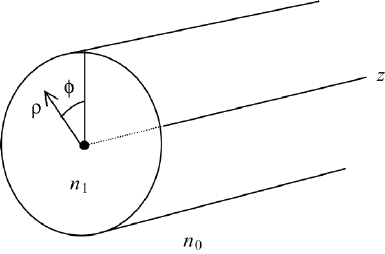
We now consider a dielectric ﬁber of radius a and homogeneous refractive

index n

in a surrounding medium of refractive index n

(Figure 6.4). Following

in general second Jackson (1975, p.364), we choose the direction of propagation

in the z direction, but use refractive indices instead of dielectric constants. We

start with the general wave equations

∂

E/∂x

+ ∂

E/∂y

+ ∂

E/∂z

 (1/c

)∂

E/∂t

(6.58)

∂

B/∂x

+ ∂

B/∂y

+ ∂

B/∂z

 (1/c

)∂

B/∂t

(6.59)

and call the differentiation with respect to the variables perpendicular to the

direction of propagation the transverse Laplacian ∇

− ∂

/∂z

Assuming periodic exponential solutions for the time dependence and the ﬁeld

in the z direction, one has the two constants (n

ω/c)

and k

after application of

the second derivative. The ratio ω/c is equal to k

in the dielectric and k is the

wave vector for the wave traveling in the Z direction. For “inside” and “outside”

6.4. FIBER OPTICS WAVEGUIDES 267

FIGURE 6.4 Coordinates for mode propagation in a ﬁber of radius a. The tranverse coordinates

are ρ and φ and the modes propagate in the z-direction.

we have

[∇

+ ((n

ω/c)

− k

)]E  0 “inside” (6.60)

[∇

+ ((n

ω/c)

− k

)]B  0 “inside” (6.61)

[∇

+ ((n

ω/c)

− k

)]E  0 “outside” (6.62)

[∇

+ ((n

ω/c)

− k

)]B  0 “outside”. (6.63)

“Inside” we may use the positiveconstant γ

 ((n

ω/c)

−k

). “Outside” we

expect an exponential decrease of the solutions and deﬁne β

 (k

−(n

ω/c)

with β real. We use cylindrical coordinates ρ and φ, and assume that we have

no azimuthal variation, which means there is no dependence on φ.Wehavetwo

differential equations for the two transversal components E

and B

, which have

Bessel functions as solutions

/dρ

+ (1/ρ)d/dρ + γ

 0 “inside” (6.64)

/dρ

+ (1/ρ)d/dρ + γ

 0 “inside” (6.65)

and

/dρ

+ (1/ρ)d/dρ − β

 0 “outside” (6.66)

/dρ

+ (1/ρ)d/dρ − β

 0 “outside”. (6.67)

We have J

(γρ) as solutions for E

and B

“inside,” and K

(βρ) for E

and

“outside.” From Maxwell’s equations we obtain relations between the ﬁeld

components depending on the “transverse” coordinates ρ and φ and the com-

ponents depending on z. The relations are divided into two groups, β

and E

depending on B

, and B

and E

depending on E

These relations are for “inside”:

 (ik/γ

)dB

/dρ B

 (in

ω/cγ

)dE

/dρ (6.68)

 (−ω/ck)B

 (ck/n

ω)E

. (6.69)

For “outside” one has a similar set of equations.

268 6. MAXWELL II. MODES AND MODE PROPAGATION

Here we treat only the TE modes, that is for a nonvanishing B

component.

One has explicitly

 J

(γρ)

 (−ik/γ)J

(γρ) “inside” (6.70)

and

 (iω/cγ )J

(γρ)

 AK

(βρ)

 (ikA/β)K

(βρ) “outside,” (6.71)

and

−(iωA/cβ)K

(βρ)

where A is a constant. Only the ﬁrst two equations of Eqs. (6.70) and (6.71)

are independent, and application of the boundary conditions at ρ  a yields the

equations:

(βa)  J

(γa) (6.72)

(−A/β)K

(βa)  (1/γ )J

(γa). (6.73)

Elimination of A results in the characteristic equation for the determination of

, written in γ and β with both depending on k,

(γa)/(γJ

(γa)) −(K

(βa)/(βK

(βa)). (6.74)

Since γ and β are both functions of k, we plot the right and the left sides of

Eq. (6.74) on the same graph, with both depending on k. At the crossing of the

curveswe get the resulting valueof k. This is shownin the second graph of FileFig

6.8. The “cutoff” frequency is obtained for J

(γa)  0, which is γa  2.405

and the corresponding wavelength is λ

{[



− n

)a2π ]/2.405}. At that

wavelength β

is 0 and k is equal to the free space value.

FileFig 6.8 (N8CWGK)

Determination of k for dielectric circular waveguide.

N8CWGK

Dielectric Circular Waveguide, Determination of k

Check for positive values of argument for J 0, J 1 and K0, K1. Since x 

(γa)

and y  (βa)

, we have for the square of the arguments of the Bessel