Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple
Подождите немного. Документ загружается.

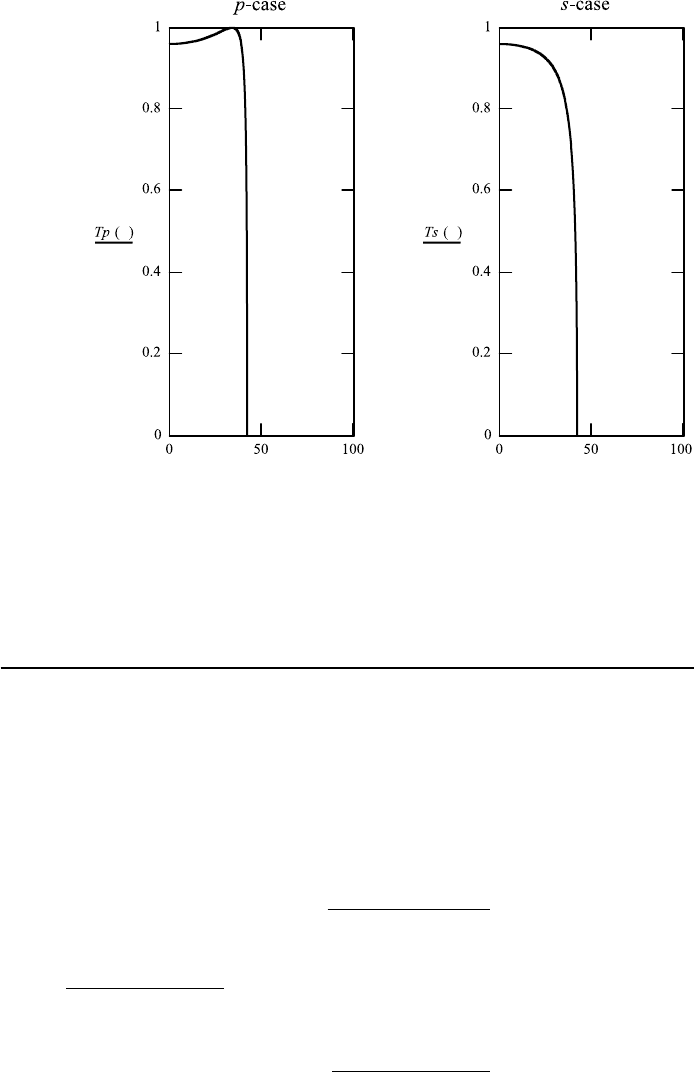
228 5. MAXWELL’S THEORY
q
q
q
q
Application 5.6.
1. Make graphs of r
2
p
, r
2
s
, t
2
p
and t
2
s
for the case where n
1
<n
2
, compare to
the graphs of the intensities, and find out which quantities, just squared, are
useful for calculation of corresponding intensities and which are not.
2. Make a graph of the factor α (n
2
cos θ
)/(n
1
cos θ ) for n
1
<n
2
and
n
1
>n
2
, compare to FileFig 5.5.
5.6.7 Total Reflection and Evanescent Wave
We look at the transmitted amplitude for the case where the angle of incidence
is larger than the critical angle. We have from (5.40)
E
t
E
to
exp i{k
2
(sin θ
t
X − cos θ
t
Y )}exp(−iωt), (5.79)
where E
to
may be calculated from Fresnel’s formulas. Using the law of refraction
as k
1
sin θ
i
k
2
sin θ
t
we may rewrite E
t
depending on the angle of incidence:
E
t
E
to
exp i{k
1
sin θ
i
X − k
2
Y
1 − (k
1
sin θ
i
/k
2
)
2
}exp(−iωt). (5.80)
The square root may be written as
i
#
n
1
sin θ
i
/n
2
)
2
− 1
$
(5.81)
and one gets
E
t
E
to
exp i
#
k
1
sin θ
i
X − k
2
Yi
#
n
1
sin θ
i
/n
2
)
2
− 1
$$
exp(−iωt). (5.82)
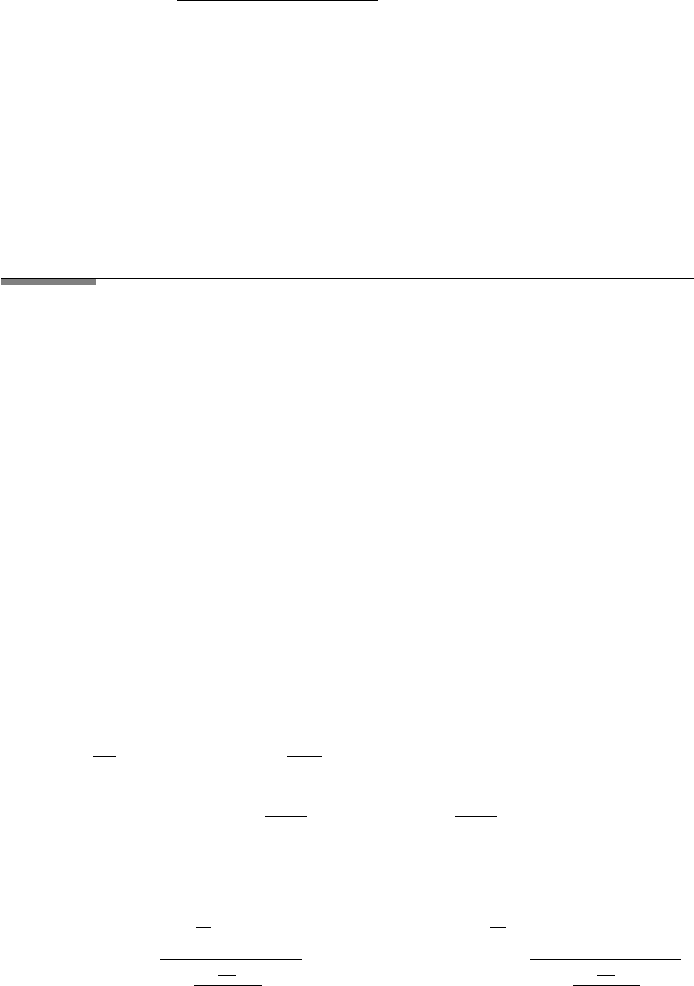
5.6. FRESNEL’S FORMULAS 229
This wave is called the evanescent wave, traveling in the medium with the lower
index of refraction in the −Y direction. It is composed of a traveling wave and
an attenuation factor. The attenuation factor is
y A exp(Yk
2
{(n
1
/n
2
)
2
(sin θ
i
)
2
− 1}, (5.83)
where k
2
(2π/λ)n
2
.
In FileFig 5.7 we show graphs of the attenuation factor depending on different
angles of incidence. One observes the rapid decrease of the magnitude depending
on penetration depth −Y
t
.
FileFig 5.7 (M7FREVA)
Graph of the attenuation factor of the amplitude of the evanescent wave for
(a)n
1
1.5, n
2
1, and critical angle θ
c
41.81, and θ
1
θ
c
+ 2;
(b) nn
1
3.4, nn
2
1, and critical angle θ
c
17.105 and θ
2
θ
c
+ 2 and
λ 0.0005mm, depending on coordinate −Y .
M7FREVA
Penetration into the Less Dense Medium at Total Reflection
Exponential factor for decrease of amplitude into the less dense medium with
−Y for two different refractive indices n1 and nn1 and n2 nn2. θc is the
critical angle. The value a is used to “be off” the critical angle. First we set
a ≡ 2 n1 ≡ 1.5 n2 ≡ 1 λ : .0005 nn1 ≡ 3.4 nn2 ≡ 1.
z : asin
n2
n1
zz : asin
nn2
nn1
Y :−0.00005, −.0001.. − .001
θ1c : z ·
360
2 ·π
θ2c : zz ·
360
2 ·π
θ1c 41.81 θ2c 17.105
θ1: θ1c + aθ2: θ2c + a
k2: 2 ·
π
λ
· n2 A : 1 kk2: 2 ·
π
λ
· nn2
y1(Y ): A · e
Y ·k2·
%
n1·
sin
(
2·π
360
·θ1
)
n2
2
−1
y2(Y ): A · e
Y ·kk2·
%
nn1·
sin
(
2·π
360
·θ2
)
nn2
2
−1
.
230 5. MAXWELL’S THEORY
To study different angles, make refractive indices the same for both and change
a to values larger than 2.
Application 5.7.
1. Study the attenuation factor for a fixed angle of incidence. Make a graph for
three indices of refraction.
2. Study the attenuation factor depending on the angle of incidence. Make a
graph for three angles of incidence for a large and a small difference of the
refractive indices n
1
and n
2
.
5.7 POLARIZED LIGHT
5.7.1 Introduction
In contrast to solutions of the scalar wave equation the solutions of Maxwell’s
equations are vector waves. In the discussion of Fresnel’s formulas, we consid-
ered the two components of the electrical field vector, parallel and perpendicular
to the plane of incidence. The two electrical field vectors vibrate in directions per-
pendicular to each other and each vector presents linear polarized light.Linearly
polarized light may be produced by reflection under the Brewster angle at the
surface of a dielectric material or when light is reflected on wire gratings with a
wavelength larger than the periodicity constant.
The superposition of two linear polarized light vectors will result in linearly
polarized light, but only if there is no phase differencebetween the two vibrations.
A phase difference may be produced by using total internal reflection and will
result in elliptically or circularly polarized light. The incident light is reflected at a
denser medium and the two components, the p-component and the s-component,
have a fixed phase angle between them, which is assumed to be zero. After
reflection, each of the two reflected components “picks up" a different phase
angle and the superposition results in a phase angle between the two components.
There are dielectric materials with different refractive indices in different
directions of the material. Plastic films, produced by stretching, may transmit
5.7. POLARIZED LIGHT
231
partially polarized light. Some of the large molecules of the material are oriented
in the direction of the stress, and the refractive index is different in the parallel
and perpendicular directions.
Uniaxial crystals have different orientations of molecules with respect to the
axis and in perpendicular layers; see below.
5.7.2 Ordinary and Extraordinary Indices of Refraction
Optical materials may have a different refractive index in one direction than in
another direction. These materials are called birefringent. Examples are quartz
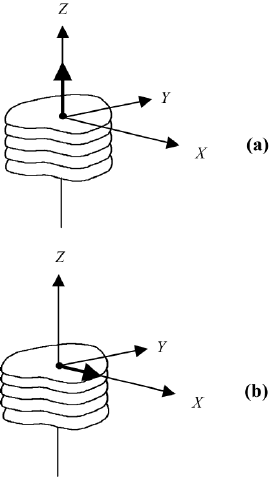
and calcite, both uniaxial crystals. These crystals are composed of layers of
atoms, which are arranged in planes, and the planes are stacked in a pile. The
atoms are symmetrically positioned in each plane and the normal of the planes
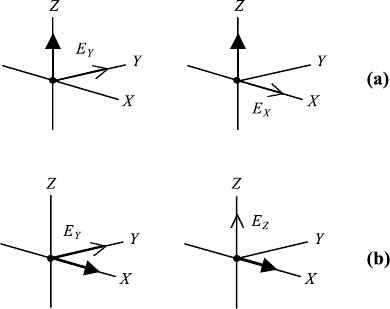
is the symmetry axis (Figure 5.5). We use an X, Y , Z coordinate system. The
symmetry axis is Z and the X and Y axes are in the plane and perpendicular to
each other.
The refractive index along the Z-axis is different from the index along the
X- and Y -axes. The refractive index along the Z-axis is called the extraordinary
index n
e
and along the X and Y -axes ordinary index n
0
.
FIGURE 5.5 Propagation with respect to the optic axis (Z), shown by black arrows: (a) wave
propagating parallel to the Z-axis. Possible directions of the oscillating electric fields are along
the X- and Y -axes; (b) wave propagating perpendicular to the Z-axis, for example in the direction
of the X-axis. Possible directions of the oscillating electric fields are along the Y - and Z- axes.
232
5. MAXWELL’S THEORY
For quartz we have n
e
1.553 and n
0
1.544 (positive crystal);
For calcite we have n
e
1.486 and n
0
1.658 (negative crystal).
The velocity of light in the medium is calculated from v c/n. For quartz the
velocity along the Z-axis is smaller than along the X- and Y -axes and Z is called
the slow axis. Crystals where the optical axis is the slow axis are called positive
crystals. For calcite the velocity along the Z-axis is faster than along the X- and
Y -axes and Z is called the fast axis. Crystals where the optical axis is the fast
axis are called negative crystals.
5.7.3 Phase Difference Between Waves Moving in the
Direction of or Perpendicular to the Optical Axis
The refractive index is related to the polarization of the atoms in the direction of
the oscillating E-vector. As a result, the velocity of propagation is determined
by the direction of vibration of the E-vector that is perpendicular to the direction
of propagation. In Figure 5.6a we show waves propagating in the Z direction,
but vibrating in the X and Y directions, which are in the plane of the layers
perpendicular to the Z direction. The ordinary index determines the velocity of
propagation, which is the same for both. In Figure 5.6b we show two waves
propagating in the X direction, but one oscillates in the Y direction and the
other in the Z direction. The velocity of the wave vibrating in the Y direction is
determined by the ordinary index n
0
, whereas the velocity of the wave vibrating
in the Z direction is determined by the extraordinary index n
e
. These two waves
propagate with different velocities in the X direction and therefore will develop
a phase difference.
FIGURE 5.6 (a) Propagation parallel to the optical axis, vibrations perpendicular to the optical
axis; (b) propagation perpendicular to the optical axis in X direction, vibrations perpendicular and
parallel to the optical axis.
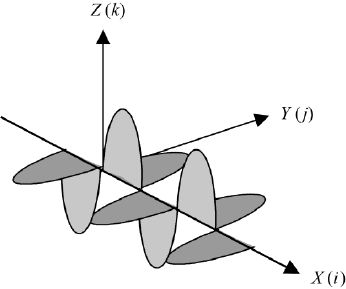
5.7. POLARIZED LIGHT 233
FIGURE 5.7 Waves with electrical vectors E
Y
and E
Z
propagating in the X direction.
For two waves, traveling in the X direction and having the same refractive
index in the Y and Z directions (Figure 5.7) we have
E
Y
jAe
i(k
1
X−ωt)
(5.84)
E
Z
kAe
i(k
1
X−ωt)
, (5.85)
taking equal amplitudes of the electrical field vectors.
Assuming that the material has a refractive index n
1
for the wave vibrating
in the Y direction and index n
2
for the wave vibrating in the Z direction with
corresponding wave vectors k
1
and k
2
, we write
E
Y
jAe
i(k
1
X−ωt)
(5.86)
E
Z
kAe
i(k
2
X−ωt)
. (5.87)
Using
φ
X
(k
2
− k
1
)X (5.88)
we have
E
Y
jA exp i(k
1
X − ωt) (5.89)
E
Z
kA exp i(k
1
X − ωt + φX). (5.90)
In Figure 5.8 we show an example of two waves with a phase difference of φ.
5.7.4 Half-Wave Plate, Phase Shift of π
We consider the case where φ
x
π and have from Eq. (5.88) for the corre-
sponding distance X π/(k
2
− k
1
). At this distance there is a phase difference
of π between the E
Y
and the E
Z
components, compared to the E
Y
and the E
Z
components at X 0 (Figure 5.9). We apply this to the case of quartz using n
e
for
the Z component and n
0
for the Y component and k
1
2πn
0
/λ, k
2
2πn
e
/λ
and have
X π/(2πn
e
/λ − 2πn
0
/λ) (λ/2)/(n
e
− n
0
). (5.91)
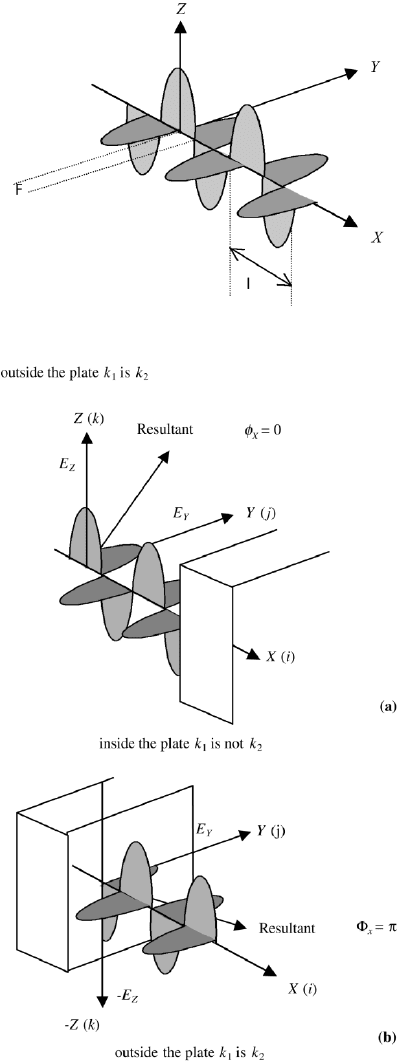
234 5. MAXWELL’S THEORY
FIGURE 5.8 Waves vibrating in the E
Y
and E
Z
directions with a phase difference of φ. The waves
are drawn at a time instant where e
iωt
1.
FIGURE 5.9 Two comonents of linearly polarized light passing throug a half-wave plate: (a)
incident, (b) emerging.

5.7. POLARIZED LIGHT 235
This distance X is very small, but any odd integer of X will have the same effect.
Therefore one may use a plate of thickness
L
h
(λ/2)(1 + 2m)/(n
e
− n
0
), (5.92)
where m is an integer. Since n
e
is larger than n
0
we have a positive value for L
h
,
and therefore quartz has been marked above as a positive crystal.
The case of calcite is reversed. We have n
e
smaller than n
0
so L
h
is a negative
value. Consequently calcite is called a negative crystal.
In FileFigs.8 we first look at the plane X 0. In the first graph the Y and
Z components are plotted as functions of X and in the second graph the Z
component is plotted against the Y component. The third and fourth graphs
show what happens in the plane X L
h
, after a phase shift of π. In the third
graph the Y and Z components are plotted as functions of X and the phase
change of the Z component is shown. In the fourth graph the Z component is
plotted against the Y component. The direction of the resulting vibration of the
two waves is shifted by 90
◦
from the second to the fourth graph (and not by π
(or 180
◦
).
FileFig 5.8 (M8POLIN)
Graphs of the superposition of the E
Y
and E
Z
components before entering the
plate, where the phase angle φ
X
0, and at the plate X L with phase angle
φ
X
π.
M8POLIN is only on the CD.
Application 5.8. Make graphs for φ
X
−π (−180) and compare with φ
X
0
and φ
X
(180) and with Figure 5.9.
5.7.5 Quarter Wave Plate, Phase Shift
π/2
We now consider the case where φ
X
π/2 and have the distance X
(π/2)/(k
2
− k
1
). There is a phase difference of π/2 between the E
Y
and E
Z
components at this distance, compared to the E
Y
and E
Z
components at X 0
(Figure 5.10). We apply this to the case of quartz using n
e
for the Z component,
and n
0
for the Y component, and k
1
2πn
0
/λ, k
2
2πn
e
/λ, and have
X (π/2)/(2πn
e
/λ − 2πn
0
/λ) (λ/4)/(n
e
− n
0
). (5.93)
This distance is very small, but any odd integer of X will have the same effect.
Therefore one may use
L
q
(λ/4)(1 + 4m)/(n
e
− n
0
), (5.94)
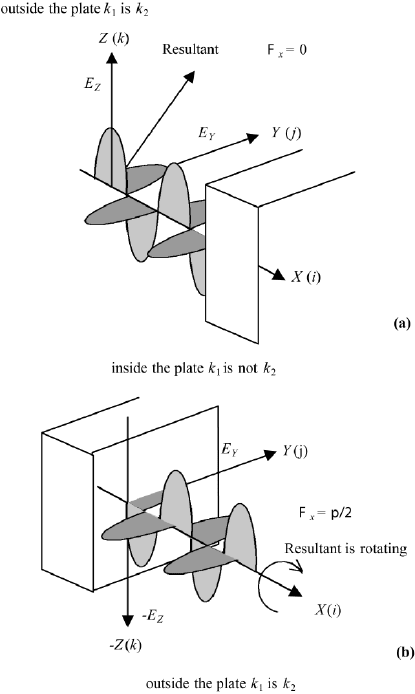
236 5. MAXWELL’S THEORY
FIGURE 5.10 Phase relation of the two components of polarized light: (a) before entering; and
(b) emerging from a quarter-wave plate.
where m is an integer. Since n
e
is larger than n
0
we have a positive value for L
q
,
and therefore quartz has been marked above as a positive crystal, and calcite is
called a negative crystal.
For the quarter-wave plate we have, with Eqs. (5.89) and (5.90),
E
Y
jA exp i(k
1
L
q
− ωt) (5.95)
E
Z
kA exp i(k
1
L
q
− ωt + π/2). (5.96)
To make a graph of the superposition of the E
Y
and E
Z
components, we take
the real parts of the fields as the values at the Y - and Z- axis of Eqs. (5.95) and
(5.96)
E
Y
cos(k
1
L
q
− ωt) (5.97)
E
Z
cos(k
1
L
q
− ωt + π/2). (5.98)

5.7. POLARIZED LIGHT 237
Or converting Eq. (5.98),
E
Y
cos(k
1
L
q
− ωt) (5.99)
E
Z
−sin(k
1
L
q
− ωt). (5.100)
We may write Eqs. (5.99) and (5.100), for a certain time interval, as E
Y
cos(−2πx
1
/360) and E
Z
cos(−2πx
1
/360 + π/2). The time interval corre-
sponds to a certain distance in the direction of propagation and to a certain angle
interval x
1
/360. In FileFig 5.9 we show four graphs, corresponding to intervals
of angles from 1
◦
to 90
◦
,1
◦
to 160
◦
,1
◦
to 235
◦
, and 1
◦
to 315
◦
. Looking onto the
paper, in the direction of the source, we see that the resulting vibration describes
a circle. The circle develops for positive φ
X
+π/2 in a counterclockwise di-
rection and the light is called left polarized. Considering E
Y
cos(−2πx
1
/360)
and E
Z
cos(−2πx
1
/360−π/2), for negative φ
X
−π/2, the circle develops
in the clockwise direction and the light is called right polarized.
FileFig 5.9 (M9POELIP)
Graphs of the superposition of the E
Y
and E
Z
components with positive and
negative phase angle φ
X
. Four graphs for four different time spans are shown.
M9POELIP
Circular and Elliptically Polarized Light
Graphs for circular and elliptically polarized light turning “left or right.” Four
graphs are shown, extending from 0 to 90, 0 to 160, 0 to 235, and 0 to 315 degrees.
The angle ranges (x) correspond to chosen time ranges. Left and right polarized
light is described by positive or negative π/2 in one component: Positive
: we have y Ey A cos(−x), yy Ez A cos(−x +) −A sin(−x);
negative : we have y Ey A cos(−x), yy Ez A cos(−x − )
A sin(−x). We write for Ez bA sin(x). When looking in the direction of the
incoming light, b −1 is for “left” polarized light (counterclockwise), b 1
for “right” polarized light (clockwise).
x1: 1, 2 ...90 x2:
1, 2 ...160
x3: 1, 2 ...235 b ≡−1 x4: 1, 2 ...315
y1(x1) : cos
−2 ·π ·
x1
360
y2(x2) : cos
−2 ·π ·
x2
360
y3(x3) : cos
−2 ·π ·
x3
360
y4(x4) : cos
−2 ·π ·
x4
360
