Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple

Подождите немного. Документ загружается.

198 4. COHERENCE

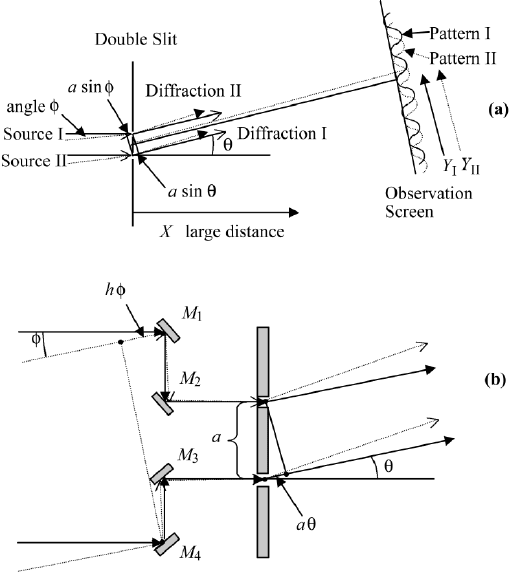
FIGURE 4.4 Michelson stellar interferometer: (a) light waves from two stars, I and II, forming

an angle φ when they arrive at a double slit of width a. The waves from each star produce a fringe

pattern on a screen at distance X, described by the coordinate Y

and Y

; (b) four mirrors are

added, M

to M

, to produce a new optical path difference hφ for the incident light, where h is

adjustable. The angle θ is the diffraction angle.

have

[π(aθ −h

φ)/λ]  (π/2)(2m) (4.22)

and for the following minimum

[π(aθ −h

φ)/λ]  (π/2)(2m + 1). (4.23)

The difference for h

−h

 λ/2φ and φ is obtained since h

−h

can be mea-

sured. This type of modiﬁed interferometer was applied to measure the angular

diameter of Betelgeuse in the Orion constellation. At the Mt. Wilson observatory

an interferometer was used with a distance h of the two mirrors of 302 cm (121

in.). The angle was determined to be 22.6 × 10

−8

rad. The distance to the star

was known from parallax measurement and the diameter was determined to be

about 300 times that of the sun. A simulation with a numerical example is given

in FileFig 4.5. The graph shows a plot of the interference pattern for assumed

values of h and φ. We determine the two values of h for observance and disap-

4.1. SPATIAL COHERENCE 199

pearance of fringes. Application of h

−h

 λ/2φ results in the angle and that

must be the angle we had to assume for the simulation.

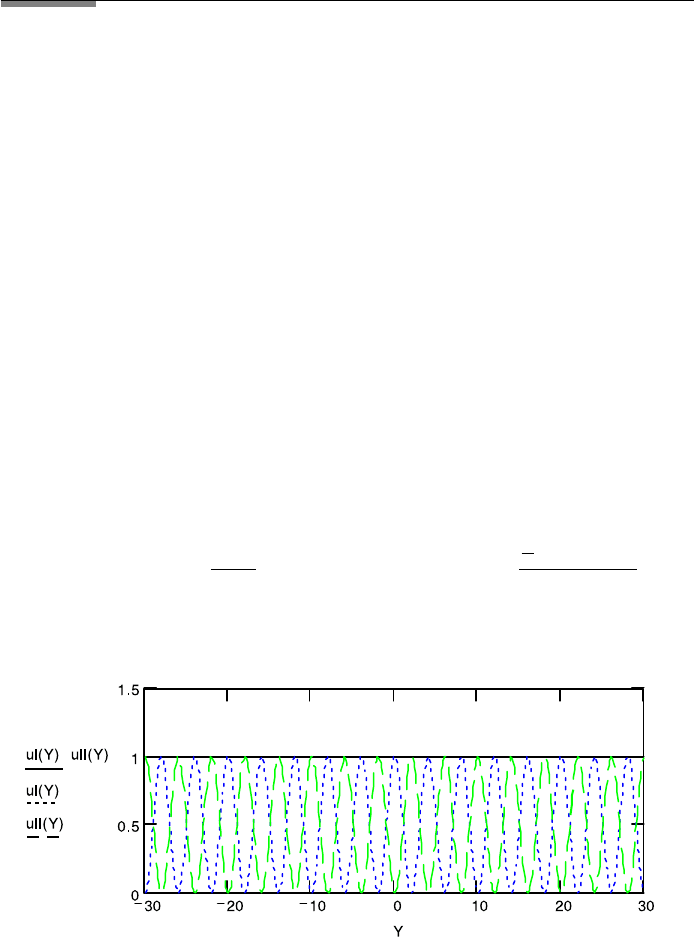
FileFig 4.5 (C5MICHSTS)

Graphs are shown of the resulting intensity interference pattern of u

and u

depending on values of h over the range Y −20 to 20. The distance from

source to interferometer is X  4000, wavelength λ  0.0005, separation in

the interferometer a  0.5. For the simulation we have to use a value for the

angle we actually want to determine and choose φ  0.00005. We then can

determine the h values of the minima and maxima and they must satisfy the

relation h

− h

 λ/2φ.

C5MICHSTS

Michelson’s Stellar Interferometer

Diffraction angle is Y/X, wavelength λ, and angle to be determined is . In-

terferometer distance of mirrors M1 and M4 is h. In the real setup we change

h to go from fringe pattern to no fringe pattern. From the difference of these

two values we calculate the angle . In this simulation we choose an angle 

and show that the fringe pattern changes for the two values of h we determine.

Example h equals 100 and 95.

Y :−30, −29.9.. 30  ≡ .00005 X : 4000 λ : .0005 d ≡ .5

uI (Y ): cos



π · d ·



X · λ



uI I (Y ): cos



π ·

· d − h · 



h ≡ 95

This is an indication of the presence or absence of fringes.

200

4. COHERENCE

Application 4.5. Change the wavelength to 0.00055 and ﬁnd φ from observed

values of h2 −h1.

4.2 TEMPORAL COHERENCE

4.2.1 Wavetrains and Quasimonochromatic Light

We have studied in Chapter 2 the superposition of monochromatic waves and

their amplitude and intensity pattern. In this section we examine ﬁnite wave-

trains and their superposition. Monochromatic waves are inﬁnitely long. The

sum of a number of monochromatic waves with wavelengths in a certain wave-

length interval results in a periodic wave. However, when integrating over the

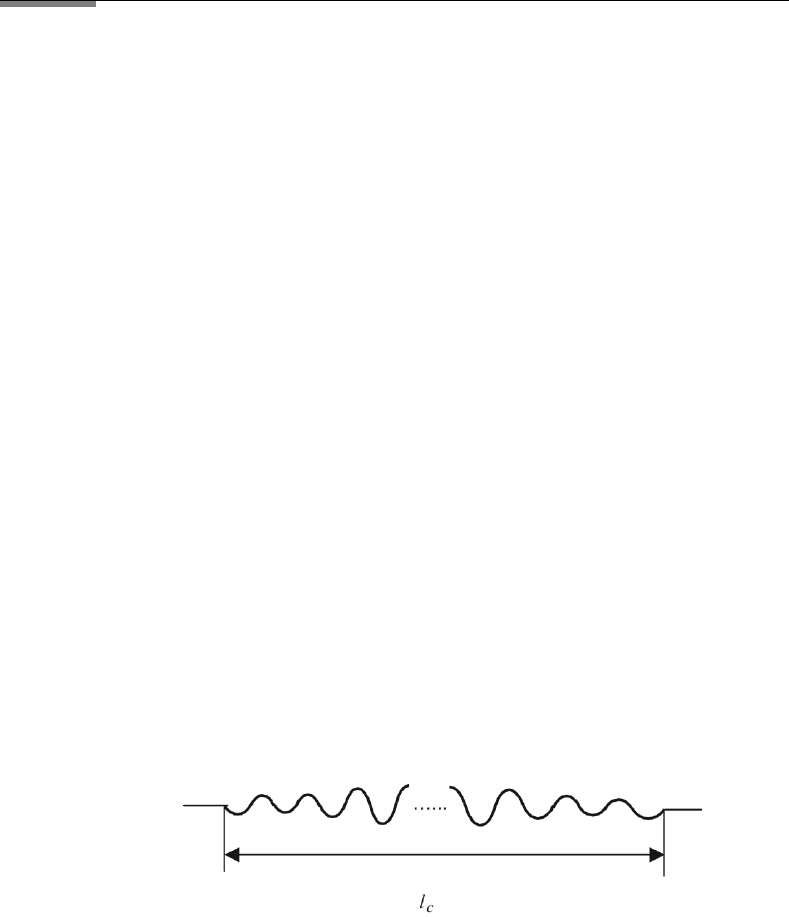
wavelength interval, one obtains a ﬁnite wavetrain, (see Figure 4.5). The wave-

train appears with decreasing amplitude for large distances. The length of the

wavetrain x  l

is proportional 1/ν, where ν is the frequency interval

corresponding to the wavelengthinterval λ of the wavetrain.The average wave-

length of the wavetrain is called λ

. The reciprocity of x and ν comes from

Fourier transformation theory. The “window” in the space domain is l

and ν is

the “window” in the frequency domain. The product x and ν is a constant and

appears in modiﬁed form in quantum mechanics as the “uncertainty relation.”

Wavetrains which satisfy the condition

λ/λ

 1 (4.24)

are called quasimonochromatic light.

To get an idea of how the waveform appears for quasimonochromatic light,

we show in the ﬁrst graph of FileFig 4.6 the superposition of four waves having

wavelength λ  1.85, 1.95, 2.05, and 2.15 for medium wavelength λ

 2.

In the second graph we show the waveform for the integration over the same

wavelength interval.

u(Y ) 



{cos(2πx/λ)}dλ. (4.25)

FIGURE 4.5 Schematic of a wavetrain of ﬁnite length l

. One refers to l

as the coherence length.

4.2. TEMPORAL COHERENCE 201

FileFig 4.6 (C6SUPERS)

First graph: Sum of four waves with wavelength λ  1.85, 1.95, 2.05, and 2.15

for medium wavelength λ

 2. Second graph: Integration over the wavelength

range from λ  1.85 to 2.15.

C6SUPERS is only on the CD.

Application 4.6.

1. Extend the x coordinate to larger ranges to see more of the periodicity for

the “summation" case and the decrease for the integration case.

2. Study the waveform for different wavelength intervals for both cases.

3. Extend the sum of four to a larger sum of different wavelengths, but keep the

wavelength interval constant. Compare with the integration case.

4.2.2 Superposition of Wavetrains

In Chapter 2 we studied interference fringes produced by monochromatic light.

For the magnitude of the superposition of two monochromatic waves with optical

path difference δ, we have used cos(πδ/λ).

Interference fringes may be observed for quasimonochromatic light of narrow

width of wavelength λ. In FileFig 4.7 we show the amplitude pattern of the

superposition of two wavetrains. The interval of integration is λ  1.85 to 2.15

and three optical path differences are considered, δ  0,

, and λ

I (Y ) 



[{cos(2π(x − δ)/λ)}+{cos(2π(x)/λ)}]dλ. (4.26)

The optical path difference of δ  0 corresponds to constructive interference for

δ  (1/2)λ

to destructive interference and for δ  λ

again to constructive

interference. The resulting amplitude of the case of destructive interference is

not zero, but much smaller than for constructive interference. We see that the

interference pattern decreases for larger and larger values of x. In FileFig 4.8 we

have calculated the intensity pattern, corresponding to the cases of constructive

interference, δ  0, and δ  λ

, and destructive interference, δ 

FileFig 4.7 (C7COHTEMS)

Amplitude pattern

of superposition of two wavetrains. Graphs 1 to 3: Integration

of waves over wavelength range from λ  1.85 to 2.15, having optical path

differences of λ  0,

, and λ

, respectively.

202 4. COHERENCE

C7COHTEMS is only on the CD.

Application 4.7. Change the wavelength interval to smaller values and

approach

in 1: the corresponding case of the monochromatic wave;

in 2: the corresponding monochromatic case for destructive interference;

in 3: the corresponding monochromatic case for constructive interference.

FileFig 4.8 (C8COHINTS)

Intensity pattern of superposition of two wavetrains. Graphs 1 to 3: Integration

of waves over wavelength range from λ  1.85 to 2.15, having optical path

differences of δ  0,

, and λ

, respectively.

C8COHINTS is only on the CD.

Application 4.8. Change the wavelength interval to smaller values and

approach

in 1: the corresponding case of the monochromatic wave;

in 2: the corresponding monochromatic case for destructive interference;

in 3: the corresponding monochromatic case for constructive interference.

4.2.3 Length of Wavetrains

The length of ﬁnite wavetrains (see Fig. 4.5) may be determined with a Michelson

interferometer. The incident light is divided at the beam splitter into two parts

traveling to M

and M

, respectively (see Fig. 4.6a). Each part is reﬂected by

a mirror and travels back to the beamsplitter (Fig. 4.6b). At the beam splitter,

the reﬂected part of the light from M

and the transmitted part of the light from

are superimposed and travel to the detector (Fig. 4.6c). When the mirror

in the Michelson interferometer is displaced, the light traveling to the detector

shows a superposition pattern of two wavetrains of ﬁnite length. First, the well-

known pattern of the superposition of two monochromatic waves appears. At a

certain large distance this pattern disappears. The wavetrain from one arm of the

Michelson interferometer will “miss” the other wavetrain because of the ﬁnite

length of the wavetrains (see Fig. 4.6d). As an example we may look at the

emission of light from

Kr at 6056.16

A. Since the wavetrain has a length of

about 1 m and displaces the one mirror by 1/2 meter because of reﬂection, the

interference is not observable. For this reason one calls the length of the wavetrain

the coherence length. For most atomic emission processes the coherence length

is much smaller whereas resonance in laser cavities may produce a much longer

coherence length of the order of 10

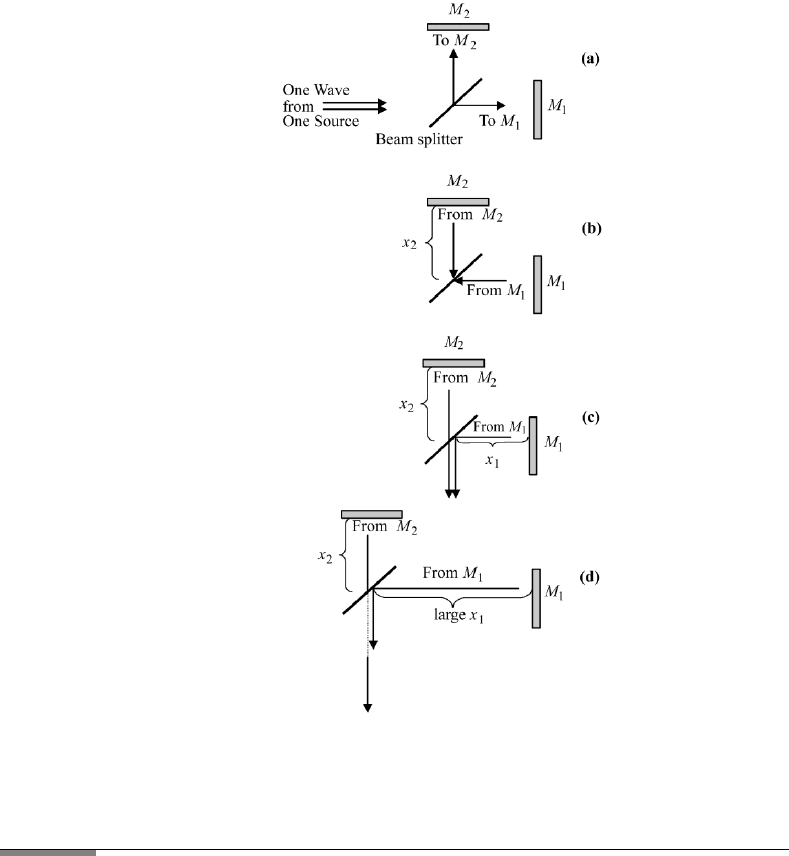
4.2. TEMPORAL COHERENCE 203

FIGURE 4.6 Splitting of the incident light in a Michelson interferometer: (a) incident light;

(b) reﬂected light traveling to beam splitter; (c) two waves traveling to the detector; (d) for large

displacements of M

, a ﬁnite wavetrain “misses” recombination with its “counterpart.”

APPENDIX 4.1

A4.1.1 Fourier Transform Spectrometer and Blackbody

Radiation

Blackbody radiation contains a large band of wavelengths and has a coherence

length with respect to the medium wavelength λ

, of only a few wavelength’s. If

we consider a series of ﬁlters with smaller and smaller band width, the coherence

length of the light passing these ﬁlters has increasingly larger and larger values.

Michelson’s interferometer may be used for Fourier transform spectroscopy, as

discussed in Chapter 9. When using blackbody radiation, the total bandwidth of

204 4. COHERENCE

the incident light has to be limited to the interval from 0 to a highest frequency,

determined by the sampling theorem. The Fourier transform process analyzes

the light and determines the intensity of the resolution width ν, which is equal

to 1/2 L where L is the length of the interferogram in meters. This length L may

be increased to larger values and consequently ν is decreased. Therefore the

length of the corresponding wavetrain l

is increasing. This process comes to a

halt when the signatures of the interferogram are obscured by noise.

In comparison, the size of the coherence length of the atomic emission of

Kr has its limitation in a time-limited emission process whereas when using

blackbody radiation in Fourier transform spectroscopy, the coherence length is

limited by the available signal-to-noise level.

See also on CD

PC1. Two Source Points (see p. 185).

PC2. Extended Sourc.(see p. 190).

PC3. Visibility (see p. 194).

PC4. Caparison of Visibilities (see p. 194).

PC5. Calculation of the Visibility for Fresnel’s Mirror Interferometer (see p.

193 and 93).

PC6. Michelson Stellar Interferometer (see p. 195).

PC7. Quasimonochromatic Light (see p. 198).

PC8. Quasimonochromatic Light and Interferogram (see p. 199).

CHAPTER

Maxwell’s

Theory

5.1 INTRODUCTION

In Chapter 2, we discussed the wave theory of light, developed a model to su-

perimpose waves, and described the resulting interference pattern in terms of

intensity depending on wavelength. The model was based on the scalar wave

equation, butin addition we made reference to electromagnetic theory.Weneeded

to take into account that a light wave changes its wavelength when traveling

through a medium of refractive index n and also used Fresnel’s formulas. Elec-

tromagnetic theory is described by Maxwell’s equations. The ﬁrst hint that light

is electromagnetic radiation came from electromagnetic experiments not involv-

ing visible light. In the analysis of the experiment a constant appeared which had

the value of the speed of light. From relativity theory we know that the speed c of

light is a fundamental constant and the ultimate limit of speed. We derive from

Maxwell’s theory and the laws of reﬂection and refraction, as we assumed in the

chapter on geometrical optics, that light travels in straight lines. We also may

derive from Maxell’s equations what we used in the chapters on interference and

diffraction and obtained from the scalar wave equation.

In this chapter we describe light by electrical and magnetic ﬁeld vectors and

discuss the polarization of light. At each point in space there are two ﬁeld vec-

tors vibrating in the perpendicular direction: taking boundary conditions into

account we derive Fresnel’s formulas. Electromagnetic theory is the basis for

the description of all optical phenomena as long as quantum effects are not

involved.

Maxwell’s equations are a mathematical formulation of the electromagnetic

laws of Faraday, Ampere, and Gauss. Maxwell analyzed the mathematical

structure of these experiments, added some terms suggested by similarities in

appearance of the electric and magnetic ﬁelds, and formulated the four equations

205

206 5. MAXWELL’S THEORY

bearing his name. Today we write Maxwell’s equations in vector notation and

call B the magnetic ﬁeld vector. This point is well explained by Feynman in his

Lecture Notes, Volume II, pp. 32–34.

The four Maxwell’s equations may be written as

∇×E −∂B/∂t

∇×B  j/ε

+ ∂E/∂t (5.1)

∇·E  ρ/ε

∇·B  0,

where E is the electrical ﬁeld vector, B the magnetic ﬁeld vector, j the current

density vector, ρ the charge density, and ε

 8.854×10

−12

F/m the permittivity

of vacuum. The mathematical form of the differential vector operator ∇ and its

scalar “square" ∇

is given in Appendix 5.1.

For light propagating in a vacuum, we have j  0 and ρ  0 and Maxwell’s

equations are reduced to

∇×E −∂B/∂t

∇×B +∂E/∂t (5.2)

∇·E  0

∇·B  0.

From this set of equations we arrive at the wave equations for the vectors E and

B as shown in Appendix 5.1.

∂

E/∂x

+ ∂

E/∂y

+ ∂

/E/∂z

 (1/c

)∂

E/∂t

(5.3)

∂

B/∂x

+ ∂

B/∂y

+ ∂

/B/∂z

 (1/c

)∂

B/∂t

. (5.4)

5.2 HARMONIC PLANE WAVES AND THE

SUPERPOSITION PRINCIPLE

5.2.1 Plane Waves

We consider a nondispersive medium.A plane wave solution of the wave equation

for the electrical ﬁeld components vibrating in the y direction and propagating

in x direction may be written as

 E

cos{2π(x/λ − t/T)}, (5.5)

where E

is the magnitude of the electrical ﬁeld, λ the wavelength, t the time,

and T the period of vibration. Equation (5.5) may be rewritten, introducing the

wave vector k  2π/λ, and the angular velocity ω  2π/T . Using exponential

notation we have

 E

exp i(kx − ωt). (5.6)

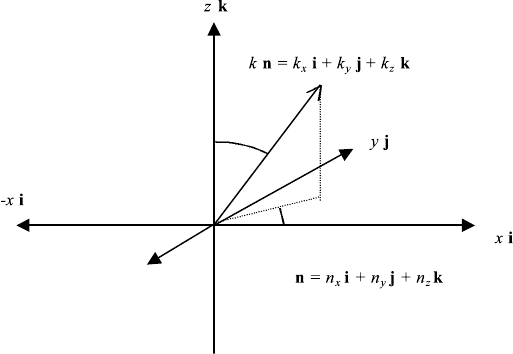
5.2. HARMONIC PLANE WAVES AND THE SUPERPOSITION PRINCIPLE 207

FIGURE 5.1 Coordinate system for a wave with wave vector kn  2π/λn, traveling in x, y, z

space. Using k here must be distinguished from k, the unit vector in the z direction. The vector r

points from 0 to a point in space with the coordinates (x,y, z).

Introduction of Equation (5.6) into the wave equation results in

ω/k  v (here v  c), (5.7)

where ω/k is the phase velocity.

To extend the propagation to any direction in x, y, z space we use vector

notation. For the description of the plane waves we choose in the x, y, z space

the coordinate axes xi, yj, and zk, where i, j, k are unit vectors and a point in x,

y, z space is given as r  xi +yj +zk. (Note that k is used for the wave vector

and for the unit vector in z direction.) When solving Eq. (5.4) by “separation

of variables" one obtains for the wave vector in the direction of propagation

kn  k

i + k

j +k

k, where n is a unit vector and k  2π/λ (Figure 5.1). We

need to ﬁnd the components k

, k

, and k

for a wave moving in x, y, z space in

direction n. To do this we evaluate the dot product k(n · i), k(n · j), and k(n · k)

and obtain for k

, k

, and k

(Figure 5.1),

 (2π/λ) · sin φ cos θ

 (2π/λ) · sin φ sin θ (5.8)

 (2π/λ) · cos φ.

For the special case of the E

component moving in the x direction we have

θ  0

◦

and φ  90

◦

, and get (Chapter 2),

 E

exp i{2πx/λ − 2πt/T}. (5.9)

For the case of E

moving in the x-z plane, one has θ  0

◦

kn  k

i +k

k  (2π/λ)(sin φi +cos φk) (5.10)