Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple
Подождите немного. Документ загружается.


3.5. BABINET’S THEOREM 167
FIGURE 3.23 Examples of complementary screens.
The general appearance of the diffraction pattern on the observation screen is
the same, regardless of one screen having larger openings than the other.
Let us consider two gratings, both having periodicity constant a. One has
a width of opening d
1
and the other of d
2
. These gratings are complementary
screens when d
1
+d
2
a. To get the diffraction pattern, we apply the Kirchhoff–
Fresnel integral to the openings of each screen. The two integrals must add up to
zero since there are no openings to integrate. We assume there is a single wave
incident on all openings and use far field approximation,
ϕ
1
(Y ) C
φ(y)(e
ik(yY)/X
)dy and ϕ
II
(Y ) C
φ(y)(e
ik(yY)/X
)dy
openings of screen I openings of screen II (3.67)
and have for the amplitudes
ϕ
I
(Y ) +ϕ
II
(Y ) 0orϕ
I
(Y ) −ϕ
II
(Y ), (3.68)
and for the intensities
[ϕ
I
(Y )]
2
[ϕ
II
(Y )]
2
. (3.69)
The diffraction pattern of the two screens has the same overall appearance. The
first equation tells us that the two diffraction patterns are “out of phase” by 180

168 3. DIFFRACTION
FIGURE 3.24 Diffraction patterns of complementary screens show the same intensity pattern.
degrees and the second one tells us that the diffraction patterns of the two screens
are similar.
In Figure 3.24 we show schematically the diffraction pattern of two comple-
mentary screens. One screen is made of open squares and the other of black
squares. In FileFig 3.15 we consider two amplitude gratings with complementary
open areas as complementary screens. The appearance of the diffraction pattern
is the same, but the heights of the peaks are different. We assumed that d
1
is
different from d
2
and therefore the open areas are different.
FileFig 3.15 (D15FABAGRS)
Two complementary screens are considered. Both are amplitude gratings of pe-
riodicity constant a. One has the width d
1
of open strips, the other the width
d
2
, and since we assume that a d
1
+ d
2
the screens are complementary. The
diffraction patterns are shown as P
1
for the grid with d
1
and P
2
for the grid
with d
2
. One observes that the diffraction patterns are similar. Both patterns
have peaks at the same location. However, they have different intensities. The
different intensities result from the different d
1
and d
2
values and consequently
different areas of integration.
D15FABAGRS
Babinet’s Theorem
Diffraction on two amplitude gratings, one with width of openings d1, the other
with width of opening d2, and both having center-to-center distance of strips
a d1 +d2. Wavelength λ, distance from gratings to screen X, and coordinate
on screen Y . All distances and wavelengths area in mm; both have number
of lines N. Normal incidence. D1 and D2 are the diffraction factors, I is the
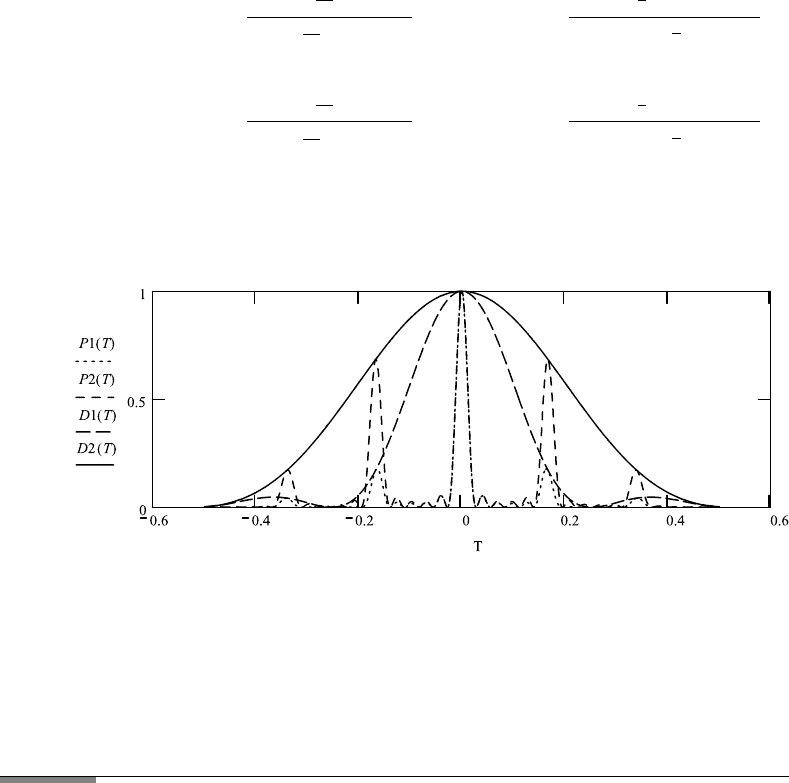
3.6. APERTURES IN RANDOM ARRANGEMENT 169
interference factor, normalized to 1. P (A) is the product of interference and
diffraction factor. Diffraction pattern of the two complementary screens: one is
a grating of width of opening d1, the other of d2, and the periodicity constant
is a d1 +d2.
θ :−.5001, −.4999 ....5
D1(θ):
sin
π ·
d1
λ
· sin(θ )
π ·
d1
λ
· sin(θ )
2
I (θ ):
sin
π ·
a
λ
· sin(θ ) ·N
N · sin
π ·
a
λ
· sin(θ )
2
λ ≡ .0005 N ≡ 6 P 1(θ): D1(θ) · I (θ)
D2(θ):
sin
π ·
d2
λ
· sin(θ )
π ·
d2
λ
· sin(θ )
2
I (θ ):
sin
π ·
a
λ
· sin(θ ) ·N
N · sin
π ·
a
λ
· sin(θ )
2
d2 ≡ .001 d1 ≡ .002 a ≡ d1 + d2 P 2(θ): D2(θ) · I (θ).
We see that the intensity of the diffraction peaks is different for the two com-
plementary patterns, but the position of the peaks is the same, and that is what
Babinet’s Principle tells us.
Application 3.15.
1. Keep a d1+d2 constant and change the width d1 to a much smaller value
than d2. Check how the intensities of the two patterns are affected.
2. For comparison, make d1 and d2 about equal.
3. Change the constant “a” to see how the pattern is changing.
3.6 APERTURES IN RANDOM ARRANGEMENT
In Chapter 2 we studied the interference pattern of an array and found that the
pattern disappears when the array is changed to a random arrangement. We now
study the question of what happens to an interference diffraction pattern if we
assume a random arrangement.
We consider an amplitude grating and want to describe the changes of the
interference diffraction pattern when we change the periodic array into a random
170
3. DIFFRACTION
arrangement. The diffraction pattern is described by the product of the diffraction
and interference factors
P
periodic
{[sin(πd sin θ/λ)]/[(πd sin θ/λ)]}
2
·{[sin(πNa sin θ/λ)]/[(N sin(πasin θ/λ)]}
2
. (3.70)
As discussed in the chapter on interference, the interference factor will average
to a constant when the change to the random array of apertures is done and we
are left only with the diffraction factor
P
random
{[sin(πd sin θ/λ)]/[(πd sin θ/λ)]}
2
. (3.71)
The random array of many openings of width d will give us the diffraction pattern
of a slit at the observation screen.
In FileFig 3.16 we have a one-dimensional calculation. The first graph shows
the interference diffraction pattern of a grating, and the second graph shows what
is left if the interference factor disappears. In FileFig 3.17 we show the diffraction
pattern of a 2-D grating as a 2-D contour plot. The first graph showsthe diffraction
pattern of the periodic arrangement and the second graph shows the diffraction
pattern of the random arrangement.This is schematically shownin Figure 3.25 for
periodic and random arrangements of square apertures.The periodic arrangement
shows the interference diffraction pattern, and the random arrangement appears
as the superposition of the intensity diffraction pattern of squares.
FileFig 3.16 (D16FAGRRANS)
The product P 1 of a diffraction and interference factor for a one-dimensional
grating is shown. When changing the periodic arrangement of the apertures to
a random arrangement, the interference factor is a constant and P 2 shows the
remaining diffraction pattern.
D16FAGRRANS is only on the CD.
FIGURE 3.25 (a) Diffraction pattern of a periodic array of rectangles; (b) diffration pattern of a
random array of rectangles. The resulting pattern is the superposition of the intensity diffraction
pattern of rectangles.
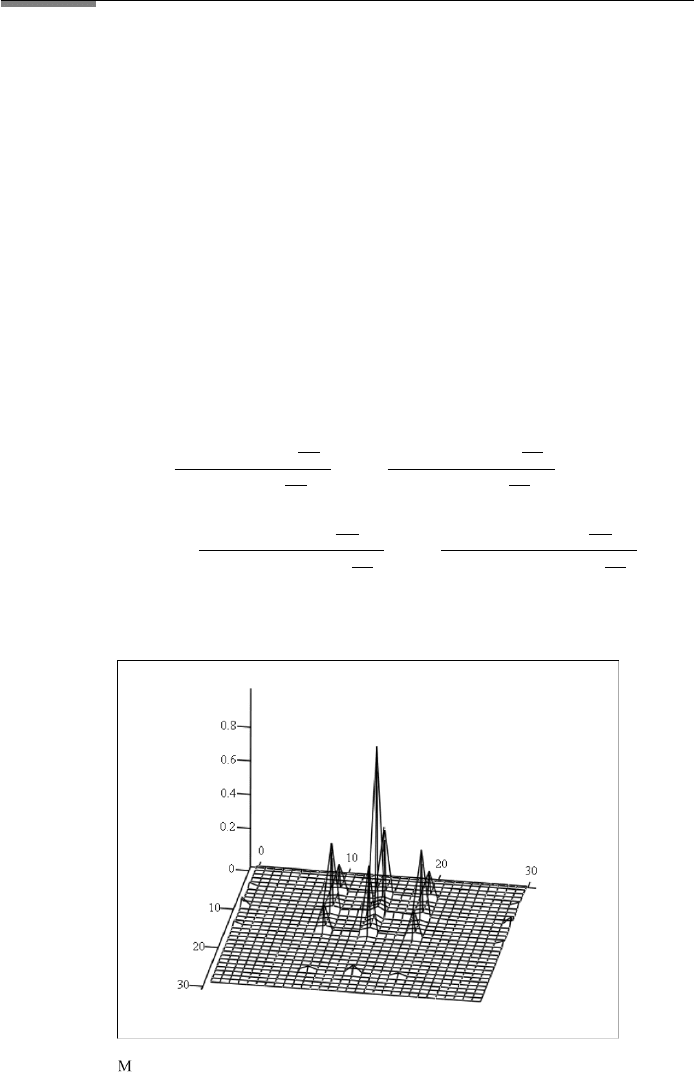
3.6. APERTURES IN RANDOM ARRANGEMENT 171
FileFig 3.17 (D17ARAYRA3DS)
The product f (x, y) of intensity of diffraction and interference factor for a two-
dimensional grating is shown. Three-dimensional plots are shown for regular
and random arrays.
D17ARAYRA3DS
3-D Graph of Diffraction Pattern
Periodic array of rectangular apertures compared to the diffraction pattern of
rectangular apertures in a random array.
1. Periodic array
i : 0 ...N j : 0 ...N
λ ≡ 4 x
i
: (−3) + .20001 · iy
j
: (−4) + .20001 · jp: 6
f (x, y):
sin
2 ·π · d ·
x
2·λ
2 ·π · d ·
x
2·λ
2
·
sin
2 ·π · d1 ·
y
2·λ
2 ·π · d1 ·
y
2·λ
2
·
⎡
⎣
sin
2 ·π · a ·
x·p
2·λ
p · sin
2 ·π · a ·
x
2·λ
2
·
sin
2 ·π · a1 ·
y·p
2·λ
p · sin
2 ·π · a1 ·
y
2·λ
2
⎤
⎦
M
i,j
: f
x
i
,y
j
d ≡ 2 d1 ≡ 2 a1 ≡ 4 a ≡ 4
N ≡ 40.
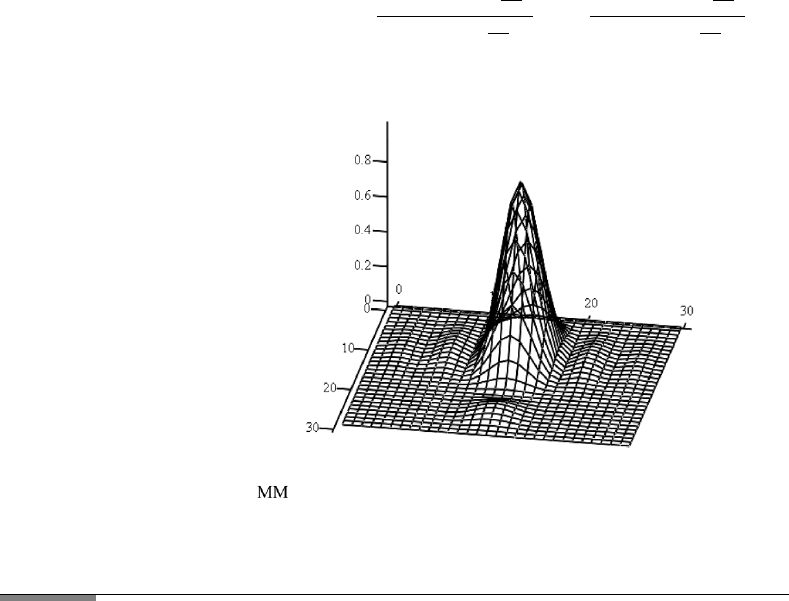
172 3. DIFFRACTION
2. Random array
f 1(x, y):
sin
2 ·π · d ·
x
2·λ
2 ·π · d ·
x
2·λ
2
·
sin
2 ·π · a ·
y
2·λ
2 ·π · a ·
y
2·λ
2
MM
i,j
: f 1
x
i
,y
j
.
3.7 FRESNEL DIFFRACTION
At the beginning of this chapter we used Fresnel diffraction for the calculation
of the Poisson spot. The Kirchhoff–Fresnel integral was applied to a round stop
and we found a constant illumination in the shadow of the round aperture on
the axis of the system. We are now interested in discussing the diffraction on
an edge, which was done by Fresnel using the integrals named after him. The
first steps are to study the Fresnel diffraction on a slit and give the definitions of
Fresnel’s integrals.
3.7.1 Coordinates for Diffraction on a Slit and Fresnels
Integrals
We consider the Kirchhoff–Fresnel diffraction integral in small angle approxi-
mation; see Eq. (3.20).
G(Y ) C
y
2
d/2
y
1
−d/2
exp[ik(1/2X)(Y − y)
2
]dy (3.72)

3.7. FRESNEL DIFFRACTION 173
and set the constant C equal to 1. To get to the definition of Fresnel’s integrals,
we change coordinates
(y −Y )
2
η
2
(λX/2) (3.73)
and have
η (Y − y)
2/λX (3.74)
and for the limits of integration η
1
and η
2
,
η
1
(Y + d/2)
2/λX and η
2
(Y − d/2)
2/λX. (3.75)
Substituting Eqs. (3.74) and (3.75) into the integral, Eq. (3.72) results in
G(η)
η
2
η
1
e
i(π/2)η
2
dη. (3.76)
We may write
η
2
η
1
e
i(π/2)η
2
dη
η
2
η
1
cos[(π/2)η
2
]dη + i
η
2
η
1
sin[(π/2)η
2
]dη (3.77)
and have for the right side of Eq. 3.77
η
2
0
cos[(π/2)η
2
]dη −
η
1
0
cos[(π/2)η
2
]dη
+ i{
η
2
0
sin[(π/2)η
2
]dη −
n
1
0
sin[(π/2)η
2
]dη}. (3.78)
The Fresnel integrals are defined as:
C(η
)
η
0
cos[(π/2)η
2
]dη, S(η
)
η
0
sin[(π/2)η
2
]dη. (3.79)
In FileFig 3.18 we show graphs of Fresnel’s integrals.
FileFig 3.18 (D18FEFNCS)
The integrals C(η
) and S(η
) are plotted as C(Y ) and S(Y ) for Y 0 to 5.
D18FEFNCS is only on the CD.
3.7.2 Fresnel Diffraction on a Slit
Fresnel diffraction on a slit is calculated using the coordinates of a slit of width
d as shown in Fig. 3.26. From Eq. (3.73) and (3.76) we have for the amplitude
at the observation point
G(Y ) C[η
2
(Y )] −C[η
1
(Y )] +i{S[η
2
(Y )] −S[η
1
(Y )]}, (3.80)

174 3. DIFFRACTION
FIGURE 3.26 Coordinates for the calculation of the Fresnel diffraction pattern of a single slit of
width d.
where the dependence on Y is
η
1
(Y + d/2)
(2/λX) and η
2
(Y − d/2)
(2/λX). (3.81)
The intensity is
I (Y ) {C[η
2
(Y )] −C[η
1
(Y )]}
2
+{S[η
1
(Y )] −S[η
1
(Y )]}
2
. (3.82)
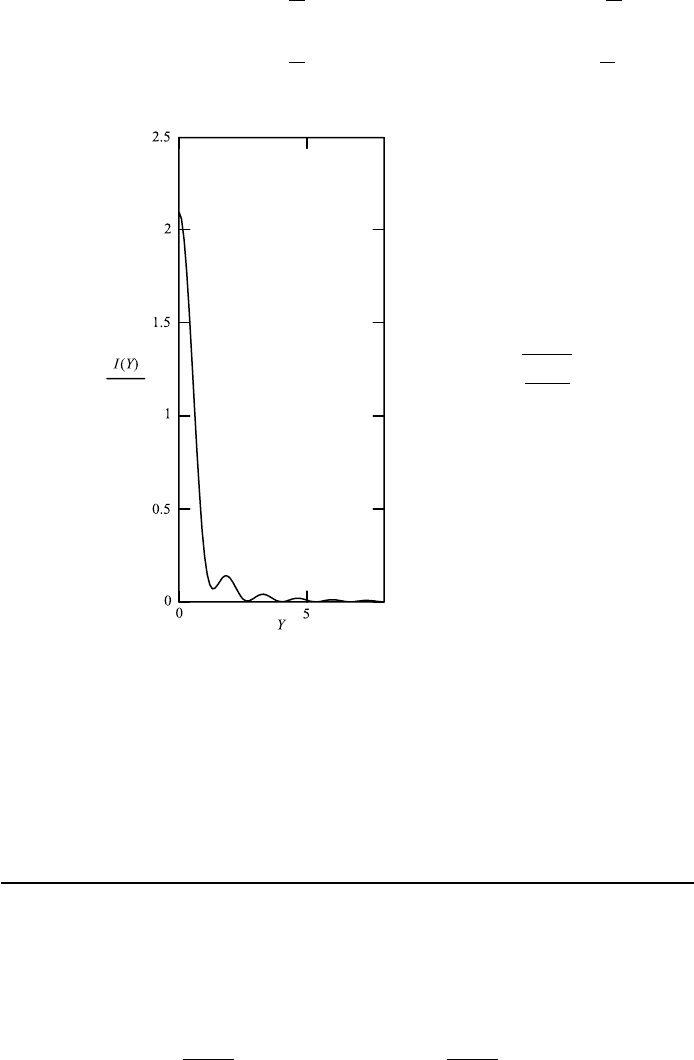
The graph in FileFig 3.19 shows Fresnel diffraction on a slit. One observes
that for the parameters used, the first minimum of the pattern is not zero. By
changing d to a smaller value or X to a larger value, one may get to a zero value
for the first minimum.
FileFig 3.19 (D19FESLITS)
Fresnel diffraction I (Y ) is plotted for a slit of width d at distance X 4000 mm
for λ 0.0005 mm. These are the same values as used in FileFig 3.3 for far
field approximation. For a small slit width, there is no difference. For a larger
slit width, the Fresnel diffraction is not zero for the first minimum.
D19FESLITS
Fresnel’s Integrals for Calculation of Diffraction on a Slit
All units are in mm, global definition of parameters.
We call η1
Y : 0,.1 ...10.
q(Y ):
Y +
d
2
·
"
2
λ · X
We call η2
p(Y ):
Y −
d
2
·
"
2
λ · X
3.7. FRESNEL DIFFRACTION 175
C
q
(Y ):
q(Y )
0
cos
π
2
· η
2
dη C
p
(Y ):
p(Y )
0
cos
π
2
· η
2
dη
S
q
(Y ):
q(Y )
0
sin
π
2
· η
2
dη S
p
(Y ):
p(Y )
0
sin
π
2
· η
2
dη
I (Y ): (Cp(Y ) −Cq(Y ))
2
+ (Sp(Y ) −Sq(Y ))
2
.
"
2
λ · X
1
TOL ≡ .1
λ ≡ 5 ·10
−4
X ≡ 4000
d ≡ 1.5.
Application 3.19.
1. Normalize the pattern of the diffraction on a slit using Fresnel diffraction.
Make it 1 at the center, and extend the Y range to negative and positive values.
2. Add to the graph the diffraction on a slit using far field approximation. Use
the same slit width, wavelength, and distance from aperture to observation
screen.
3. For what values of d do we have close agreement?
3.7.3 Fresnel Diffraction on an Edge
Fresnel diffraction on an edge is treated as the diffraction on a large slit with
one edge at y 0 and the other at y ∞(Figure 3.27). For the slit we had the
limits for −d/2tod/2. Note the negative sign in Eq. (3.74)
η
1
(Y + d/2)
2/λX, η
2
(Y − d/2)
2/λX. (3.83)

176
3. DIFFRACTION
FIGURE 3.27 Coordinates for the calculation of the Fesnel diffraction pattern of an edge treated
as a large slit, position of slit from y 0toy (∞). For the value of the integral from 0 to −∞
we use the value −.5. The dependence on Y is now only contained in η
1
.
The integration limits are now
η
1
(Y )
2/λX η
2
−∞. (3.84)
For the edge presented by a slit with one side at y 0 and the other side at
y ∞,wehave
u(Y )
−∞
η
1
e
−i(π/2)η
2
dη C(η) + iS(η)|
−∞
η
1
. (3.85)
The integrals C(η) and S(η) have to be taken from η
1
to −∞.At−∞, both are
−.5, and we get for the intensity (not normalized)
I (Y ) {−.5 − C(η
1
)}
2
+{−.5 −S(η
1
)}
2
. (3.86)
The first graph in FileFig 3.20 shows the intensity diffraction pattern
(Eq. (3.86)) and Figure 3.28 shows a photograph of the diffraction on an edge.
The second graph in FileFig 3.20 shows how the diffraction on an edge is derived
from the diffraction on a large slit.
FIGURE 3.28 Photograph of the Diffraction on an edge. (From M. Cagnet, M. Francon, and J.C.
Thrieer, Atlas of Optical Phenomena, Springer-Verlag, Heidelberg, 1962.)
