Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple

Подождите немного. Документ загружается.

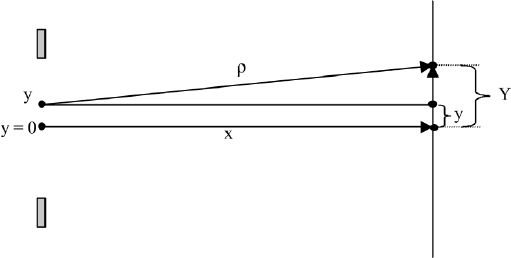
3.3. FRESNEL DIFFRACTION, FAR FIELD APPROXIMATION, AND FRAUNHOFER OBSERVATION

137

we speak of Fresnel diffraction. We use small angle approximation to show the

differences in these approaches to diffraction.

3.3.1 Small Angle Approximation in Cartesian Coordinates

Since the distance from aperture to observation screen is large, we may use

small angle approximation for the diffraction angle. We consider the integral in

Eq. (3.4),



(A/R) exp(ikR)(1/ρ) exp(ikρ) cos θdσ (3.15)

opening of aperture

and neglect the cos θ factor. The factor (A/R) exp(ikR) is a constant and can be

taken before the integral. Using only a one-dimensional approach for the Y and

y directions, we have further to consider,

u(Y )  C



ikρ

)/ρ dy. (3.16)

opening of aperture

The coordinates are shown in Figure 3.8, using X for the distance from the

aperture to the screen. Since the distance X between the observation screen and

the aperture is large, we take ρ in the denominator as a constant, but not in the

exponential. We develop ρ using the coordinates of Figure 3.8 and have

ρ 



(Y − y)

+ X

1/2

 X + (1/2X)(Y − y)

. (3.17)

Inserting Eq. (3.17) into (3.16) and including 1/ρ and e

ikX

in a new constant C



we have

u(Y )  C



exp{ik(1/2X)(Y − y)

} dy. (3.18)

opening of aperture

FIGURE 3.8 Coordinates for small angle approximation.

138 3. DIFFRACTION

We write the exponent of Eq. (3.18) as

ik{+(1/2X)(y

) + (1/2X)(Y

) − (yY)/X}. (3.19)

3.3.2 Fresnel, Far Field, and Fraunhofer Diffraction

3.3.2.1 Fresnel Diffraction

If we do not neglect the quadratic terms in Eq. (3.19), we are back to Eq. (3.18)

and have

u(Y )  C



exp{ik(1/2X)(Y − y)

} dy. (3.20)

opening of aperture

This is called Fresnel diffraction. The integral may be expressed using Fresnel’s

integrals.

3.3.2.2 Far Field Diffraction

In Eq. (3.19) we neglect the quadratic term in y and consider (1/2X)(Y

)asa

constant and include it in C



,wehave

u(Y )  C





−ik(yY/X)

dy. (3.21)

opening of aperture

This is the far ﬁeld approximation.

3.3.2.3 Fraunhofer Diffraction

Fraunhofer diffracton is also far ﬁeld approximation, but we do not have to go

so far, because we observe the pattern in the focal plane of a lens. In this case we

have to ﬁnd the effect on the wavefront when light is focused on the focal plane

of a lens with focal length f . We obtain the result that one has the same integral

for Fraunhofer diffraction as one has for far ﬁeld approximation.

Small angle approximation was obtained by considering in the integral the

exponent, Eq. (3.19),

ik{+(1/2X)(y

) + (1/2X)(Y

) − (yY)/X}. (3.22)

For far ﬁeld approximation we neglected the quadratic term in y and considered

the term in X and Y as a constant.

Now we do not neglect the quadratic term in y and show that this term is

compensated by the effect of the lens (for a detailed discussion see Goodman,

1988, p. 78.) We look at the wavefront passing through the lens. The wavefront

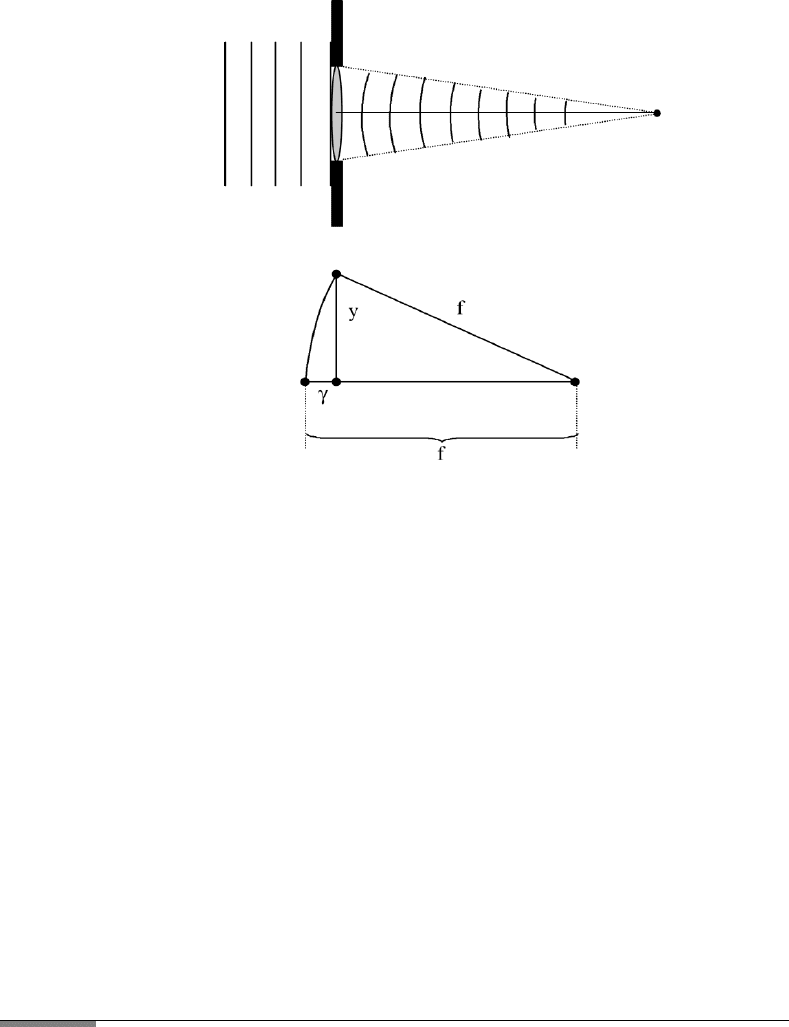
3.4. FAR FIELD AND FRAUNHOFER DIFFRACTION 139

FIGURE 3.9 Coordinates for the calculation of the change of the wavefront by a lens.

is converging to the focal point of the lens (see Figure 3.9). Over the length y

we have an increasing phase shift γ , which is calculated from

+ (f − γ )

 f

. (3.23)

Neglecting γ

in (f

− 2fγ + γ

), we have for the phase shift

γ  (y

)/2f. (3.24)

This shift must be subtracted as the phase shift in our integral. We get in the

exponent, that is, Eq. (3.22), with X  f ,

ik{+y

/2f + (1/2f )(Y

) − (yY)/f }−ik(y

)/2f. (3.25)

The new quadratic term in y cancels the old one, which we neglected in the far

ﬁeld approximation. We then have to consider

u(Y )  C





−ik(yY/X)

dy. (3.26)

This integral is the same as obtained in the far ﬁeld approximation.

3.4 FAR FIELD AND FRAUNHOFER DIFFRACTION

The far ﬁeld diffraction and Fraunhofer diffraction of the Kirchhoff–Fresnel

integral have the same mathematical appearance. The only difference is that in

140 3. DIFFRACTION

far ﬁeld approximation the diffraction pattern is observed on a faraway screen,

whereas in Fraunhofer diffraction the observation screen is placed at the focal

plane of a lens and that may be closer to the aperture.

We now discuss the diffraction pattern of various geometrical shapes of

apertures. From Eq. (3.4) we have

u(Y )  C



ikρ

) dσ, (3.27)

where dσ is the surface element of the aperture and 1/ρ has been taken before the

integral, included in C, which contains all constant terms. Note that in Eq. (3.27)

we have not used small angle approximation in the exponent.

3.4.1 Diffraction on a Slit

The diffraction on a slit is important because it is a simple one-dimensional

diffraction problem and appears in the diffraction pattern of all types of gratings

and in other diffraction-related phenomena. The coordinates for the calculation

of the diffraction on a slit are shown in Figure 3.10. We divide the opening into

N intervals y and sum up all waves traveling in direction θ. In the ﬁrst step

it is assumed that these waves are generated at the limits of all intervals and all

adjacent waves have the same optical path difference δ. This is similar to the

discussion in Chapter 2 for interference on an array (Eq. (2.107)). The optical

path difference between waves of ﬁnite steps is y sin θ and replacing qδ in the

sum of Eq. (2.107), we have



−ik(y sin θ )

. (3.28)

Making the step y inﬁnitesimally small, one gets the integral

u(Y )  C



−ik(y sin θ)

dy, (3.29)

where C includes all constant terms. The integration is from −d/2tod/2, and

we have to calculate

u(Y )  C



d/2

−d/2

−ik(y sin θ)

dy, (3.30)

or in small angle approximation with sin θ  Y/X,

u(Y )  C



d/2

−d/2

−ik(yY/X)

dy. (3.31)

The result of the integration of Eq. (3.31) is

u  Cd sin(πd sin θ/λ)/{(πd sin θ )/λ}. (3.32)

The normalized intensity is written

I  I

{sin(πd sin θ/λ)/{(πd sin θ/λ)}

. (3.33)

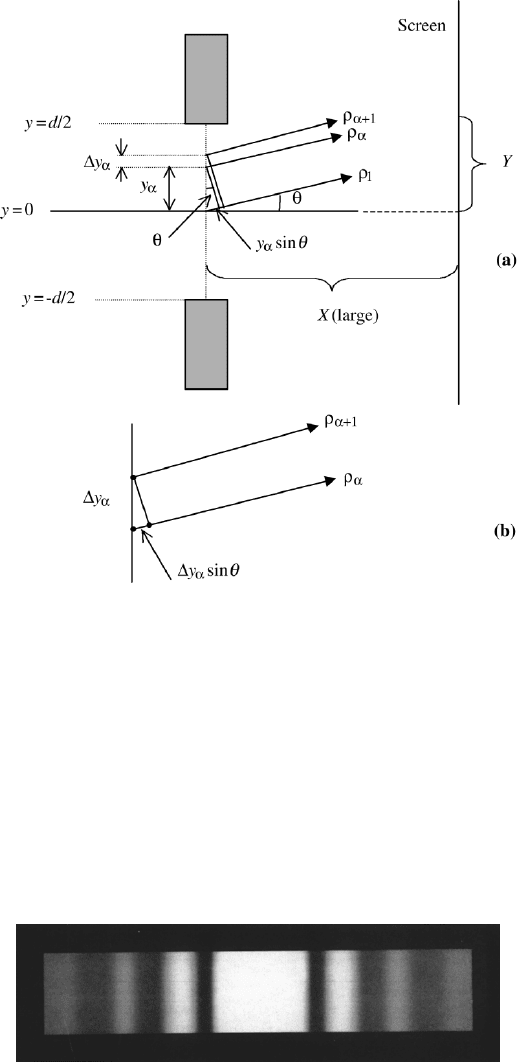
3.4. FAR FIELD AND FRAUNHOFER DIFFRACTION

141

FIGURE 3.10 Coordinates for the calculation of the diffraction on a slit: (a) phase difference of

all wavelets with respect to the center one used for the summation process; (b) path difference

between ρ

and ρ

α+1

Or in small angle approximation,

I  I

[{sin(πdY/Xλ)}/{πdY/Xλ}]

. (3.34)

The diffraction pattern of a slit has a periodic appearance with decreasing

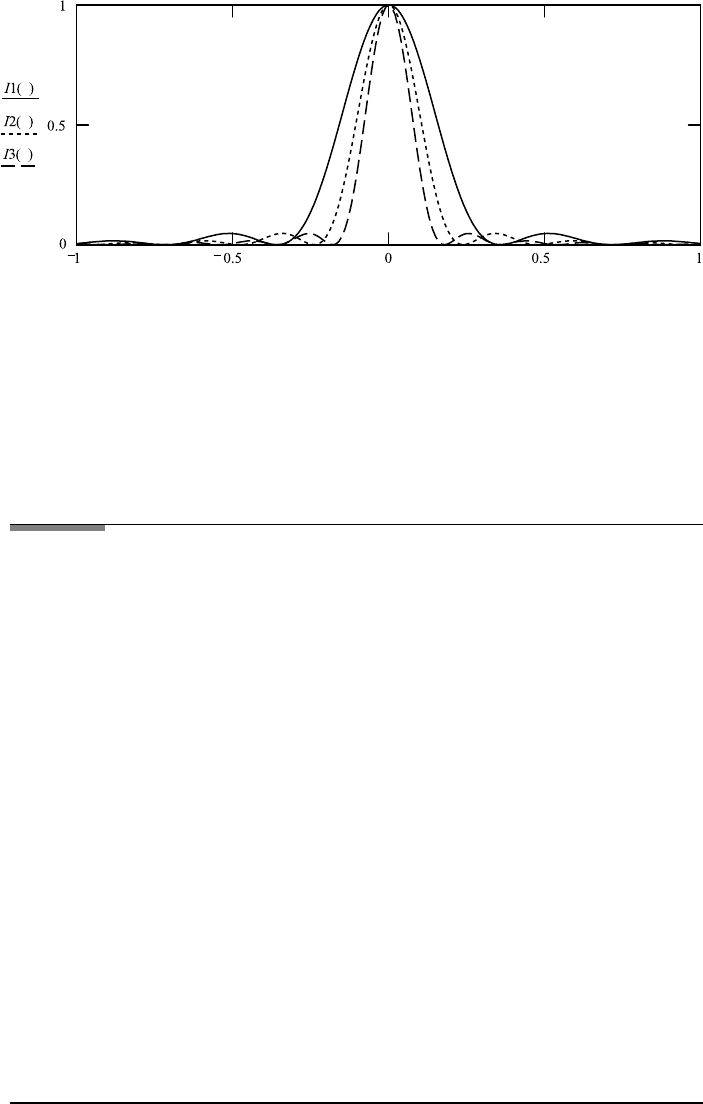
intensity of the maxima. The graph in FileFig 3.2 shows three diffraction patterns.

The wider ones are for the smaller slit openings. In Figure 3.11 we show a

photograph of a diffraction pattern of a slit. In Application FF2 the width of the

diffraction pattern with respect to changes in λ and d is studied.

FIGURE 3.11 Diffraction pattern formed by a single slit (from M. Cagnet, M. Francon, J.C.

Thrierr, Atlas of Optical Phenomena, Springer-Verlag, Heidelberg, 1962).

142 3. DIFFRACTION

The main maxima is at Y  0. At that point we have sin 0/0, and a similar

discussion to that presented in Chapter 2 results in I  I

. The angle from the

center of the slit to the ﬁrst minimum of the diffraction pattern is called the

diffraction angle θ  λ/d, and is used when discussing resolution or the Fresnel

number for characterizing the losses of a laser cavity. The side maxima are ap-

proximately at Y/X  (m+1/2)λ/d, which is approximately centered between

the minima. An exact determination is done using FileFig 3.3 and Application

FF3.

FileFig 3.2 (D2FASLITS)

A graph of the intensity of the diffraction pattern on a slit. By changing the

width d, we see that the width of the diffraction pattern is inversely proportional

to the width of the slit. By changing λ the width of the diffraction pattern is

proportional to the wavelength. This is a general property one observes for

diffraction patterns. The minima are at mλ/d.

D2FASLITS

Diffraction on a Slit of Width d at Wavelength λ

X is distance; slit-screen, Y is coordinate on screen. For small angles, Y/X is

proportional to the diffraction angle θ . MCAD notice the singularity at 0. For

the graph we get around it using the range Y −100.1, −99.1 to 100.1. All

lengths are in mm.

Three slits with different widths d1, d2, and d3:

d1 ≡ .08 d2 ≡ .12 X : 4000 λ ≡ .0005

I 1(θ ):



sin



π ·

· sin



2·π

360

· θ





π ·



2·π

360

· θ)



I 2(θ ):



sin



π ·

· sin



2·π

360

· θ





π ·



2·π

360

· θ)



d3 ≡ .16 I3(θ):



sin



π ·

· sin



2·π

360

· θ





π ·



2·π

360

· θ)



θ ≡−2, −1.99 ...1.

3.4. FAR FIELD AND FRAUNHOFER DIFFRACTION 143

Application 3.2. The dependence of the width of the diffraction pattern on values

of λ and d may be studied by changing λ to λ/2 and 2λ and d to d/2 and 4d

and considering the ratio of d/λ.

FileFig 3.3 (D3FASLITEXS)

Expanded graph of the intensity of the side maxima and minima for the diffraction

pattern on a slit, Y  18, 19 ...150, X  4000, and λ  0.0005. Numerical

determination of the values of the side maxima and minima.

D3FASLITEXS is only on the CD.

Application 3.3.

1. Give the position of the ﬁrst ﬁve minima.

2. Determine the maxima. The values of the secondary maxima are obtained

by differentiation of I  I

[sin{πdY/Xλ}/{πdY/Xλ}]

with respect to Y

and setting the resulting expression equal to 0. One may perform the differ-

entiation with a symbolic computer calculation program. One obtains the

transcendental equation πyd/λ  tan(πyd/λ), where y  Y/X. The so-

lution of the transcendental equation may be obtained by plotting πyd/λ

and tan(πyd/λ) on the same graph and using the intersections. Determine

the values of the ﬁrst ﬁve intersections, corresponding to the ﬁrst ﬁve side

maxima, and compare with the values read from the graph in FF3 and with

the approximate formula Y/X  (m + 1/2)λ/d.

3. Calculate the intensity ratio of the ﬁrst, second, and third maxima to the

zeroth maximum and compare with the theoretical values from the intensity

formula for the diffraction on a slit.

144 3. DIFFRACTION

3.4.2 Diffraction on a Slit and Fourier Transformation

The integral for the calculation of the diffraction on a slit in small angle

approximation (Eq. (3.31)), is

u(Y )  C



d/2

−d/2

exp −i2π(y/λ)(Y/X) dy, (3.35)

where we used k  2π/λ.We do the following substitutions

v  (y/λ),x Y/X, a  d/2λ (3.36)

and have

u(x)  C



exp[−i2π (ν)(x)]dν. (3.37)

To write the integral with integration limits from −∞to ∞we deﬁne the function

Q(ν)as

Q(v)  1 for x between − a and a

Q(v)  0 otherwise. (3.38)

We then have

u(x)  C



∞

−∞

Q(ν)exp−i2π (ν)(x) dν. (3.39)

The integral u(x) in Eq. (3.39) is the Fourier transform of Q(ν). We may integrate

and obtain

u(x)  C



(sin 2πax)/(2πax) (3.40)

similar to that obtained in Eq. (3.40).We havethe result that the Fourier transform

of the slit function Q(v) with opening width a is the function (sin 2πax)/(2πax)

which is sometimes called a sinc-function. When Q(ν) is not the slit function,

but given as a numerical function or a complicated analytical function, one can

not obtain an analytical expression for u(x) but one can calculate the numerical

Fourier transformation. Most computational programs offer Fourier transforma-

tion. In FileFig 3.4 we write a step function for x

with i  0 to 255, assuming

that x

 1for0tod and otherwise 0, and plot x

as a function of i/255. Here

we consider only half of the slit and do the Fourier transformation c

, shown

as the graph of c

depending on j/255, plotted from 0 to 0.5. Since we cover

with the input data only half of the slit, we get only half of the diffraction pat-

tern. However, because the Fourier transformation is real, and we have used

the fast Fourier transformation (FFT), the Fourier transformation c

shows only

N  128 points. The inverse Fourier transformation results again in 256 points.

More details on this subject are given in Chapter 9 on Fourier transformations.

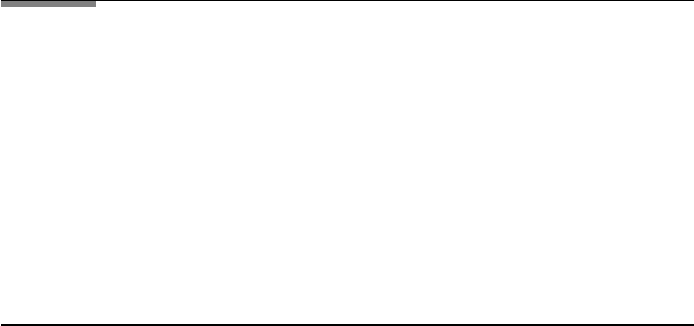
3.4. FAR FIELD AND FRAUNHOFER DIFFRACTION 145

FileFig 3.4 (D4FASLITFT)

Fourier transformation of a step function.The step function has been deﬁned for a

width of d  20. The number of points to be used is 2

−1.The real and imaginary

parts of the Fourier transformation are shown. The Fourier transformation of

the Fourier transformation is also calculated and the real part is again a step

function, and the imaginary part is 0.

D4FASLITFT is only on the CD.

Application 3.4. For several widths of the step, read off the value of the ﬁrst zero

of the transform. A formula for the value of the ﬁrst zero may be obtained from

Eq. (3.40). Compare with the value of the graph of the Fourier transformation

and with Application FF3.

3.4.3 Rectangular Aperture

The diffraction pattern of the rectangular aperture is easy to calculate as an

extension from one dimension, as used for the slit, to two dimensions. In the

next section we do it in small angle approximation and show that the integral is

useful for the calculation of far ﬁeld diffraction on a round aperture, important

for all optical devices and instruments with circular symmetry.

For the calculation of the diffraction pattern of a rectangular aperture with

dimensions d in the y direction and a in the z direction, we go back to the

integral of Eq. (3.31).

u(Y ) 



d/2

−d/2

−ik(yY/X)

dy.

Integration over the y direction will be extended to include the z direction; see

Figure 3.12. As a result, the diffraction pattern is described by a product of two

integrals of the type of Eq. (3.31), one over the opening d in the y direction and

the other over the opening a in the z direction.

u(Y, Z) 



d/2

1−d/2

exp −i2π(y/λ)(Y/X) dy



a/2

−a/2

exp −i2π(z/λ)(Z/X) dz. (3.41)

We obtain

u(Y, Z)  C{d sin(πdY/Xλ)/(πdY/Xλ){a sin(πaZ/Xλ)/(πaZ/Xλ)} (3.42)

and we have for the normalized intensity

I  I

[{sin(πdY/λX)}/{πdY/λX}]

[{sin(π aZ/λX)}/{πaZ/λX}]

. (3.43)

146 3. DIFFRACTION

FIGURE 3.12 Coordinates for the calculation of the diffraction pattern of a rectangular aperture.

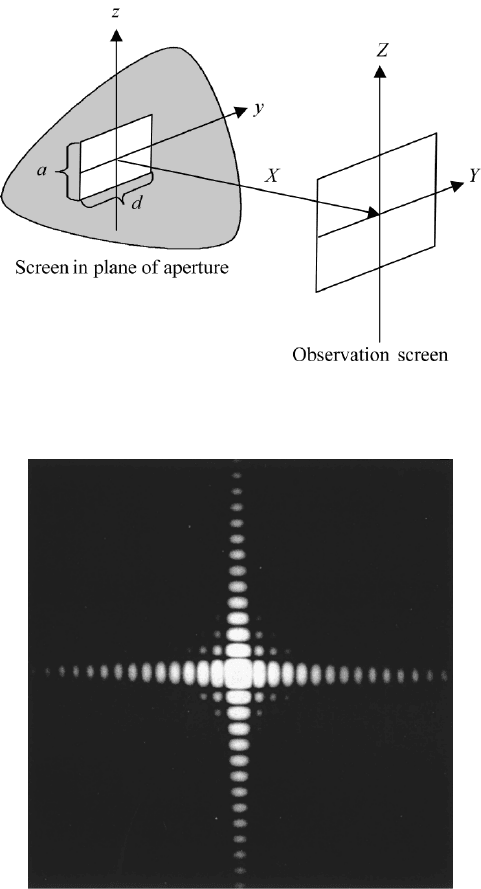
FIGURE 3.13 Far ﬁeld diffraction pattern of a rectangular aperture (from M. Cagnet, M. Francon,

and J.C. Thrierr, Atlas of Optical Phenomena, Springer-Verlag, Heidelberg, 1962).

In FileFig 3.5 we have a 3-D graph of the calculated intensity diffraction

pattern with maxima and minima in the y and z directions. The diffraction angle,

that is, the angle from the center of the aperture to the ﬁrst minimum, is in the y

direction Y/X  λ/d, and in the z direction Z/X  λ/d. A photograph of the

diffraction pattern is shown in Figure 3.13.