Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple

Подождите немного. Документ загружается.

2.5. TWO-BEAM AMPLITUDE DIVIDING INTERFEROMETRY 107

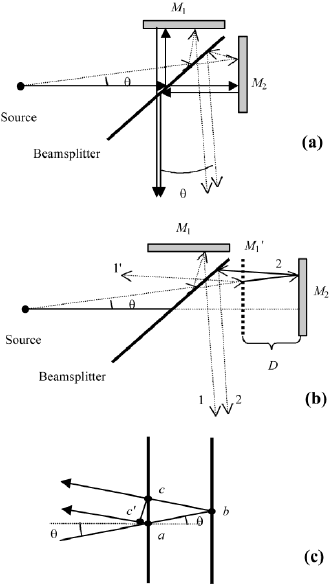
FIGURE 2.15 (a) Light passing through a Michelson interferometer for a light beam incident

under the angle θ ; (b) light passing through a Michelson interferometer for a light beam incident

under the angle θ and one arm folded onto the other; (c) calculation of path difference for a light

beam incident under the angle θ.

The intensity of the superimposed two beams is obtained as

(θ,D)  cos

(π2D(cos θ)/λ). (2.63)

When a fringe is formed by incident light under the same angle of inclination,

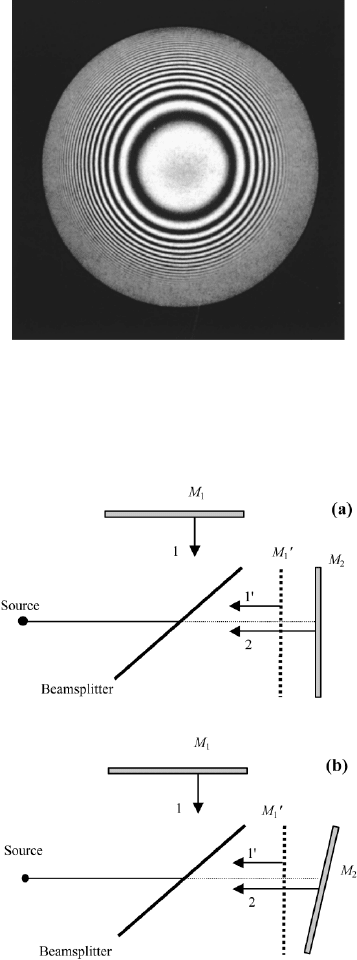
one speaks of Heidinger fringes. Heidinger fringes are shown in Figure 2.16. A

cone of light was used with a Michelson interferometer for the observation of the

ring pattern. In FileFig13. we study graphs of the cross-section of the intensity

pattern of Heidinger fringes. They are produced by the Michelson interferometer

for the dependence on the angle θ, for ﬁxed wavelength λ and for ﬁxed thickness

D. We may also produce with the Michelson interferometer fringes of equal

thickness. We fold one beam onto the other beam, as shown in Figure 2.17a, and

then consider a similar positioning as discussed for the plane parallel plate. If one

of the mirrors of the Michelson interferometer is tilted (Figure 2.17b), we have

the same situation as for the wedge-shaped gap (Figure 2.10a). Therefore, the

fringe pattern of the Michelson interferometer with one tilted mirror is similar

108 2. INTERFERENCE

FIGURE 2.16 Heidinger interference fringes observed with a Michelson interferometer. The ring

pattern is observed when using a cone of light (from Cagnet, Francon, Thrierr, Atlas of Optical

Phenomena, Springer-Verlag, Heidelberg, 1962).

FIGURE 2.17 (a) Michelson interferometer with mirror M

folded onto the other arm;

(b) Michelson interferometer with mirror M

folded onto the other arm and M

tilted.

to the wedge-shaped air gap. When a fringe is formed by incident light for the

same thickness D, one speaks of Fizeau fringes.

2.5. TWO-BEAM AMPLITUDE DIVIDING INTERFEROMETRY 109

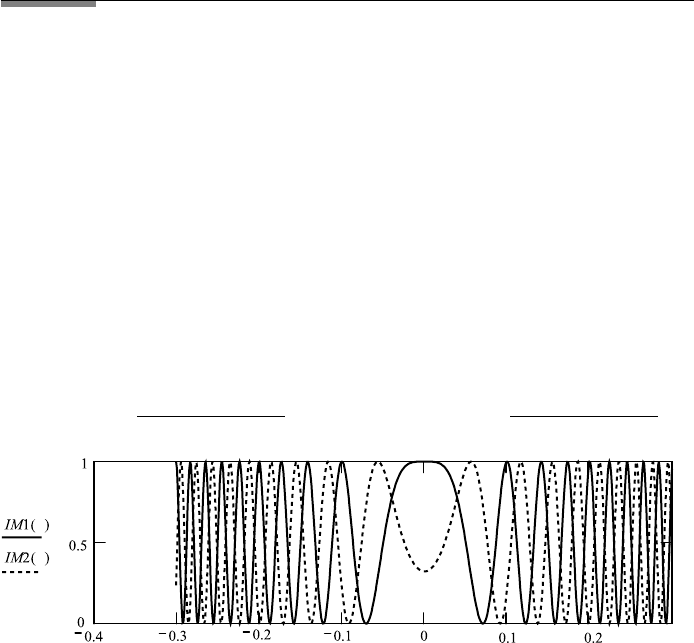
FileFig 2.13 (I3MICHANS)

Ring pattern of intensity of the Michelson interferometer depending on angle θ

for two wavelengths λ and λλ for ﬁxed D.

I13MICHANS

Michelson Interferometer, Dependence on θ

Fringe pattern depending on angle θ for two ﬁxed wavelengths λ and λλ and

ﬁxed displacement D. An ideal beamsplitter is assumed. All lengths in mm.

θ :−301, −300 ...3 λ : .0005 D : .05 λλ : 00052

IM1(θ): cos



2 ·π · D · cos(θ )



IM2(θ): cos



2 ·π · D · cos(θ )

λλ



Application 2.13.

1. Observe that the separation of the fringes for wavelengths λ and λλ gets

smaller for larger angles and that at the center, when one wavelength λ has

a maximum, the other has none.

2. Consider one wavelength only and ﬁxed angle θ . To each maximum cor-

responds an integer m determined by 2D cos θ  mπ. Use D/λ  x

for the ratio, and show that the maxima may be numbered by m(θ ) 

2x cos(2πθ/360). Make graphs for m(θ) for θ from 0 to 90 and determine

the number of rings one has for ratios of x  1, 2, 3, 4. The larger number m

belongs to the smallest angle θ. This is different fromYoung’s experiment and

similar ones, where the angle is proportional to the order of interference.

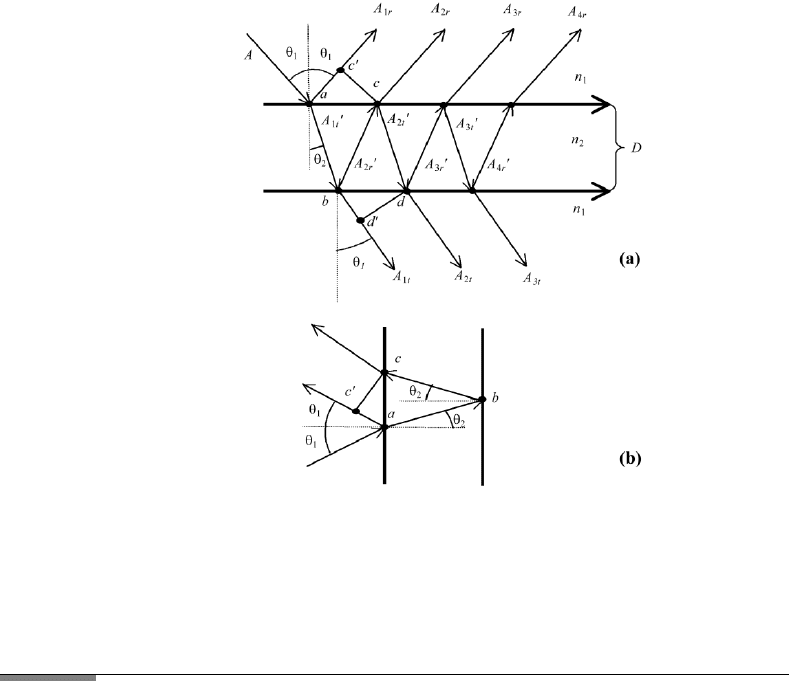
110 2. INTERFERENCE

FIGURE 2.18 (a) Geometry for multiple interference at a plane parallel plate of index n

and

thickness D. The light is incident at an angle θ

from a medium with index n  1. Using Snell’s

law at the ﬁrst and second surface one may show that the emerging angle is equal to the incident

angle θ

. The reﬂection angle within the plate is θ

; (b) geometry for the calculation of the optical

path from point a to point c



and c.

2.6 MULTIPLE BEAM INTERFEROMETRY

2.6.1 Plane Parallel Plate

In Section 5.2 we studied the plane parallel plate and considered only two re-

ﬂected waves (Figure 2.9). We formulated the condition for constructive and

destructive interference, but did not investigate the question, “Where does the

light travel?” when for destructive interference there is no light in the direction

of reﬂection. Now we want to include in our discussion all internal reﬂections of

the plate and calculate the resulting reﬂected and transmitted waves as shown in

Figure 2.18. We show that the reﬂected and transmitted intensity is equal to the

incident intensity. When we have destructive interference for the reﬂected light,

all light is transmitted and vice versa.

The incident wave is assumed to have magnitude A and makes the angle

with the normal. The plate has thickness D and a refractive index n

. The

refractive index on both sides of the plate is assumed to be 1. The magnitudes

of the reﬂected and transmitted waves are A

and A

, where i is 1, 2, 3, ...,

respectively. The calculation of the optical path difference is done by using

2.6. MULTIPLE BEAM INTERFEROMETRY 111

the wave reﬂected on the ﬁrst surface and the wave reﬂected once on the second

surface.We assume that both waves propagate in the same direction and calculate

the optical path difference, (Figure 2.18b) using the distances [ac] and [bc]. One

has [ab]  [bc]  D/ cos θ

and [ac]  [(2D/ cos θ

)(sin θ

)]]  2D tan θ

The optical path difference between A

and A

is then

δ  2n

[bc] − [ac] sin θ

 2Dn

/ cos θ

− 2D tan θ

sin θ

. (2.64)

Using the law of refraction we get

δ  2Dn

/ cos θ

− 2D tan θ

sin θ

 2Dn

cos θ

(2.65)

The same optical path difference is obtained for transmission. We call r

the

amplitude reﬂection coefﬁcient for a wave incident from medium 1 and reﬂected

at medium 2, with the corresponding intensity R

. Similarly, we call r

for a

wave incident from medium 2 and reﬂected at medium 1, with the corresponding

intensity R

. The ﬁrst index indicates the medium in which the wave travels.

The second index indicates the medium at which it is reﬂected. Similarly, we

use τ

for the absolute value of the amplitude of a transmitted wave traveling

from medium 1 to 2 and τ

in the opposite direction. We deﬁne τ



√

and τ



√

, where T

and T

are transmitted intensities. From energy

conservation we have that R

+ T

 1 and R

+ T

 1. The phase

difference  is

  (2π/λ)2Dn

cos θ

(2.66)

and a list of the reﬂected amplitudes

 Ar

 Aτ

i

 Aτ

i2

 Aτ

)

i3

(2.67)

and transmitted amplitudes

 Aτ

i

 Aτ

)

i2

 Aτ

)

i3

(2.68)

For the summation of the reﬂected amplitudes one gets

 Ar

+ Aτ

i

(1 + r

i

+ (r

i

)

+···) (2.69)

and for the transmitted amplitudes

 Aτ

(1 + r

i

+ (r

i

)

+ ...). (2.70)

11 2 2. INTERFERENCE

Using the formula for the summation process

nN−1



n0

 (1 − x

)/(1 − x) (2.71)

we see that the term of the Nth power can be neglected, since the reﬂection

coefﬁcients are all smaller than 1 and N is a large number. We now have for the

reﬂected amplitude

 Ar

+ Aτ

i

/(1 − r

i

) (2.72)

and for the transmitted amplitude

 Aτ

/(1 − r

i

). (2.73)

We call r the absolute value of the amplitude reﬂection coefﬁcients r

and r

and have for n

, using Fresnel’s formulas (Chapter 5), that r

−r and

 r; that is, R

 R

. As result one has 1 − R

 T

 1 − r

 T



1 − R

and we may use τ

 1 − r

and write

−Ar +Ar(1 − r

i

/(1 − r

i

) (2.74)

 A(1 − r

)/(1 − r

i

). (2.75)

The transmitted intensity is obtained by multiplication of A

with its complex

conjugate A

∗

 A

(1 − r

)

[1/(1 − r

i

)(1 − r

−i

)].

One has (1−r

i

)(1−r

−i

)  1−r

i

−r

−i

 1+r

−r

2 cos 

and gets

∗

 A

[(1 − r

)

]/(1 + r

− 2r

cos ). (2.76)

And similarly

∗

 A

[2r

(1 − cos )]/(1 +r

− 2r

cos ). (2.77)

Introduction of the normalized intensities





∗



and I





∗



(2.78)

results in

 [2r

(1 − cos )]/(1 +r

− 2r

cos ) (2.79)

and

 [(1 − r

)

]/(1 + r

− 2r

cos ). (2.80)

Using the abbreviation

g  2r/(1 −r

) (2.81)

2.6. MULTIPLE BEAM INTERFEROMETRY

11 3

and the trigonometric identity

cos   1 − 2 sin

(/2) (2.82)

we obtain

 [g

sin

(/2)]/[(1 + g

sin

(/2)] (2.83)

and

 1/[(1 + g

sin

(/2)], (2.84)

where we recall that   (2π/λ)δ, and δ  2Dn

cos θ

, the optical path

difference of adjacent transmitted and reﬂected waves. Corresponding to the

conservation of energy one has

+ I

 1. (2.85)

depending on the thickness D and the angle of incidence θ

, the incident intensity

is divided between I

and I

. If [sin /2]

 0, we have the condition of,

constructive interference, the reﬂected light I

 0,

δ  2Dn

cos θ

 0,λ,2λ,...,m

. (2.86)

If [sin /2]

 1 we have a minimum of light transmitted. The condition is

δ  2Dn

cos θ

 (1/2)λ, (3/2)λ,...,(m/2)λ, m odd (2.87)

and one has

 1/(1 + g

) and I

 g

/(1 + g

). (2.88)

In FileFig 2.14 we show graphs of Eqs. 2.88 for transmitted and reﬂected

intensity, depending on thickness D for ﬁxed wavelength λ and different refrac-

tive indices outside of the plate. In Figure 2.19 we show photos of interference

fringes for observation in reﬂection and transmission. The fringes depend on

the angle between the incident light and the normal of the surface. They are

FIGURE 2.19 Interference fringes observed with a plane parallel plate using an extended source:

(a) reﬂection; (b) transmission (from Cagnet, Francon, Thrierr, Atlas of Optical Phenomena,

Springer-Verlag, Heidelberg, 1962).

11 4 2. INTERFERENCE

Heidinger fringes. The reﬂection coefﬁcients, used in the graph of FileFig 2.14,

are calculated from Fresnel’s formulas for a glass plate. For the special case of

normal incidence and reﬂection on the optical denser medium, one has from

Fresnel’s formulas

r  (n

− n

)/(n

+ n

). (2.89)

In FileFig 2.15 we show graphs, assuming normal incidence, of the transmitted

and reﬂected intensity depending on wavelength for ﬁxed thickness D.InEq.

(2.81) we deﬁned g  2r/(1 − r

). We mention here that πg/2 is called the

ﬁnesse. It is used for the characterization of the quality of the Fabry–Perot,

discussed in the next chapter.

FileFig 2.14 (I14PLANIDS)

Intensity of interference at a plane parallel plate assuming normal incidence.

Graph of the reﬂection and transmission depending on thickness D for ﬁxed

wavelength and different values of n1, n2, and n3.

I14PLANIDS

Normal Incidence. Plane Parallel Plate: Reﬂected and Transmitted Intensity Depending

on Thickness for Fixed Wavelength

The reﬂection coefﬁcients are calculated from Fresnel’s formulas for θ  0. Re-

fractive indices n1, n2, and n3 may all be different and the reﬂection coefﬁcients

for both surfaces are calculated. The calculation of the fringe pattern is done

depending on D for ﬁxed λ.

  (

2π

)2dn2 θ1: 1

n1: 1 n2: 1.5 n3: 1

r12 :

n2 −n1

n2 +n1

r23 :

n3 − n2

n3 + n2

  (2π/λ)2dn2 cos θ2

r12  0.2 r23 −0.2

λ ≡ .0005 D ≡ .0002,.00021 ...002

IT(D):



1 − r12





1 − r23



1 + (r12 · r23)

− (2 · r12 · r23) ·cos



4 · π ·

· n2



IR(D): 1 − IT(D).

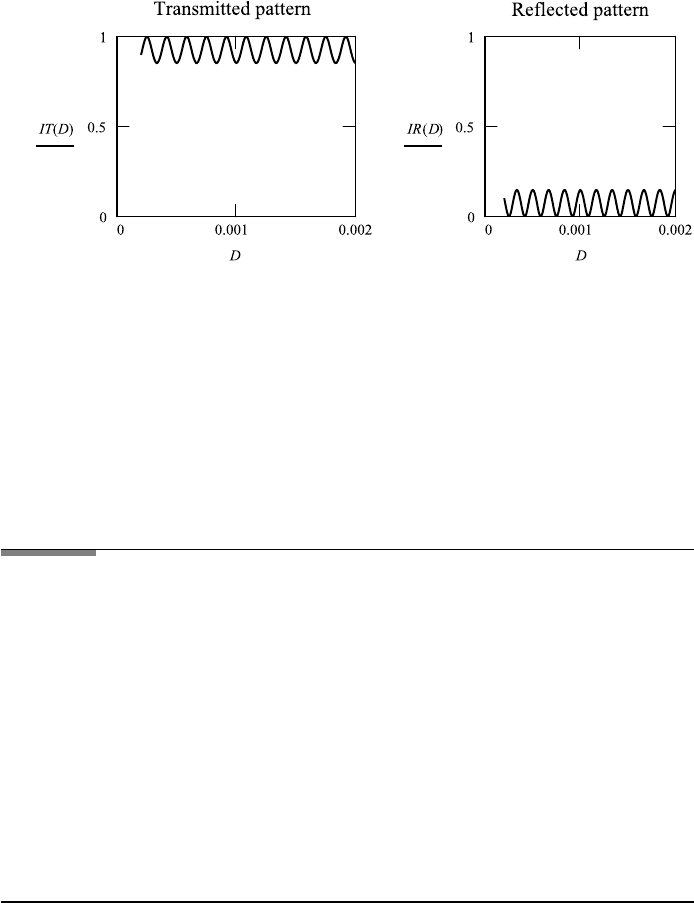
2.6. MULTIPLE BEAM INTERFEROMETRY 11 5

Application 2.14. Consider transmitted and reﬂected intensity depending on

the thickness of the plate.

1. Try out different combinations such as n1 <n2 <n3, n1 <n2 >n3, and

n1 >n2 <n3, and see the effect of the phase jump of reﬂection at the denser

medium.

2. Choose arbitrary values for r<1 and observe how the intensity is changing.

FileFig 2.15 (I15PLANIDS)

Intensity of interference at a plane parallel plate assuming normal incidence.

Graph of the reﬂection and transmission depending on wavelength λ for ﬁxed D

and different values of n1, n2, and n3.

I15PLANIDS is only on the CD.

Application 2.15. Consider the transmitted and reﬂected intensity depending

on wavelength.

1. Try out different combinations such as n1 <n2 <n3, n1 <n2 >n3, and

n1 >n2 <n3, and see the effect of the phase jump of reﬂection at the denser

medium.

2. Find the wavelength for the last fringe, depending on the thickness D of the

plate.

2.6.2 Fabry–Perot Etalon

A plane parallel plate with reﬂecting surfaces on both sides is called an etalon.

The reﬂecting layers may be made of metal or a structure of dielectric ﬁlms.

We show that for a speciﬁc wavelength at a speciﬁc spacing of two reﬂecting

surfaces, all incident light will be transmitted while a single reﬂecting surface

will transmit only a small amount.

11 6 2. INTERFERENCE

We start from the treatment of the plane parallel plate and assume that one can

replace the two interfaces with idealized reﬂectors, having the reﬂectivity r.The

medium between these two reﬂectors has refractive index 1. Assuming normal

incidence and using the reﬂectance R  r

one has from Eq. (2.81),

 4R/(1 −R)

. (2.90)

For normal incidence, one has for /2,

/2  2πD/λ. (2.91)

The reﬂected and transmitted intensities are obtained from Eqs. (2.83) and (2.84):

 g

sin

(/2)/(1 +g

sin

(/2)) I

 1/(1 + g

sin

(/2)). (2.92)

There the mathematical form of I

is called the Airy function.

If [sin /2]

 0 we have the condition of constructive interference for

transmitted light, I

 0,

δ  2D  0,λ,2λ,...,mλ. (2.93)

If [sin /2]2  1 we have a minimum of light transmitted. The condition is

δ  2D  (1/2)λ, (3/2)λ,...,(m + 1/2)λ, (2.94)

where m is an integer.The graph in FileFig 2.16 showsthree transmission patterns

for three different absolute values of the reﬂection coefﬁcient. We have chosen

λ  .1 and plotted the transmitted intensity as a function of the spacing D,

for m  1 and r  .7, .9, and .97, respectively. We see that the width of

the transmitted intensity depends on the absolute value of the reﬂectance r of

a single plate and becomes narrower when r gets close to 1. For constructive

interference, that is, when 2D  mλ, it follows that sin

/2  0. Therefore

is 1, independent of the value of r. We may have r so close to 1 that the

transmission of a single plate is almost zero, but the transmission of the pair of

plates at the right distance will be one.At this distance the Fabry–Perot etalon has

a resonance mode. In experimental Fabry–Perot etalons, the peak transmission

will not be exactly one, due to losses such as absorption in the plates. The Fabry–

Perot etalon, using high orders, is applied to investigate with high resolution

details of a spectral line in a narrow spectral range. The dependence of the width

of the spectral line on the reﬂection coefﬁcient of the etalon is shown in the graph

of FileFig 2.17. The transmittance is plotted depending on the wavelength λ for

three different reﬂection coefﬁcients r and ﬁxed distance D.