Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple

Подождите немного. Документ загружается.

2.3. SUPERPOSITION OF HARMONIC WAVES 87

2.3.2.1 Use of the Time Average

The time average of the square of a cosine function depending on t, taken over

the interval of one period, that is, from 0 to T ,is

(1/T )





cos t]

dt  1/2. (2.14)

Using for the cos-function the “second” factor of Eq. (2.8), we get

 (1/T)



[cos{2π(x/λ − t/T) − 2π(δ/2)/λ}]

dt 

(2.15)

As result, we obtain for the intensity of the wave described in Eq. (2.8),

I  [2A cos{2π (δ/2)/λ}]

(1/2). (2.16)

This is the square of the ﬁrst factor (Eq. (2.13)) multiplied by 1/2.

2.3.2.2 Complex Notation

Complex notation has its advantages, for example, when adding several har-

monic waves. Then, the intensity is calculated by the product zz

∗

and the time

dependence is automatically eliminated.

We rewritethe sum of the two real expressions of Eq. (2.5) in complexnotation:

z  z

+ z

 A exp i(2π(x)/λ − 2πt/T)

+ A exp i(2π(x − δ)/λ − 2πt/T). (2.17)

Here the real part of z, that is, Re(z), is the amplitude of u of Eq. (2.8). The

superposition of the two waves may be written in complex notation as

z  z

+ z

 A exp{−i2πt/T + i(2π (x)/λ)}

×{1 + exp(−i2πδ/λ)}. (2.18)

In the second factor of Eq. (2.18) we may factor out exp −i2πδ/2λ and then

have

z  A exp{−i2πt/T + i(2π(x)/λ)}exp(−i2πδ/2λ)

×{exp i2πδ/2λ + exp −i2πδ/2λ}. (2.19)

Using

{exp i2πδ/2λ + exp −i2πδ/2λ}2 cos 2πδ/

2λ (2.20)

one gets

z  A exp{−i2πt/T + i(2π(x)/λ)}exp(−i2πδ/2){2 cos 2πδ/2λ}. (2.21)

For simplicity we collect all phase factors into one term, call

exp{−i2πt/T + i(2π(x)/λ) − i2πδ/2λ}exp i, (2.22)

88 2. INTERFERENCE

and have

z  [2A cos(2πδ/2λ)] exp i. (2.23)

For the intensity we use the square of the absolute value of z, that is, the product

of z times its complex conjugate z

∗

 [2A cos(2πδ/2λ)] exp i[2A cos(2πδ/2λ)] exp −i (2.24)

∗

 [2A cos(2πδ/2λ)]

. (2.25)

Comparing the intensity in Eq. (2.16) with Eq. (2.25), one sees that they

are different by the factor

. This factor

is not signiﬁcant, since one usually

normalizes the results for the calculation of interference and diffraction pattern.

FileFig 2.4 (I4COSINTS)

Graphs of the real part of the superposition of two waves depending on space and

time, its square, and the time average of the “second factor.” The time-dependent

superposition of two waves is given in complex notation. Its real part and the

square of the real part are plotted. Then the product zz

∗

is plotted, depending

on x, and appearing at a constant. The “fringe pattern” is plotted (i.e., zz

∗

depending on the optical path difference.

I4COSINTS is only on the CD.

2.3.3 Normalization

To compare an interference pattern with observation, one may normalize both.

Let us assume we have an interference pattern with a maximum in the center.

The scale of the observation data may be changed in such a way that at the center

one has the intensity equal to 1. The intensity calculated from the formula will

also be changed: one divides by the value calculated at the center, and obtains

also for the intensity 1. For example, let us assume that an interference pattern

is described by f (x) and that for x  0wehavef (0)  b. Then writing

I (x)  f (x)/f (0)  I

f (x) (2.26)

with I

 1/b results in I (x) equals 1 for x  0.

In FileFig 2.4 we have plotted the real part of u and the time average and

compared it with zz

∗

, which is independent of time. We also plot what one may

call the “fringe pattern,” that is, zz

∗

, depending on the optical path difference.

2.4. TWO-BEAM WAVEFRONT DIVIDING INTERFEROMETRY

2.4 TWO-BEAM WAVEFRONT DIVIDING

INTERFEROMETRY

2.4.1 Model Description for Wavefront Division

The classical experiments by Young, Fresnel, and Lloyd were performed to

demonstrate the wave theory of light. All three experiments use one incident

wave and divide the light from the source into two waves. The two waves are

superimposed after an optical path difference is introduced and a pattern showing

the maxima and minima is observed. One calls such a pattern, consisting of max-

ima and minima, a fringe pattern. The process of splitting up the incident wave at

two small openings into two new waves involves diffraction, considered in detail

in Chapter 3. The incident wave we consider is monochromatic, propagates in

the x direction, vibrates in the y direction, and has a large lateral extension in the

z direction. The experimental setup produces two waves by wavefront division,

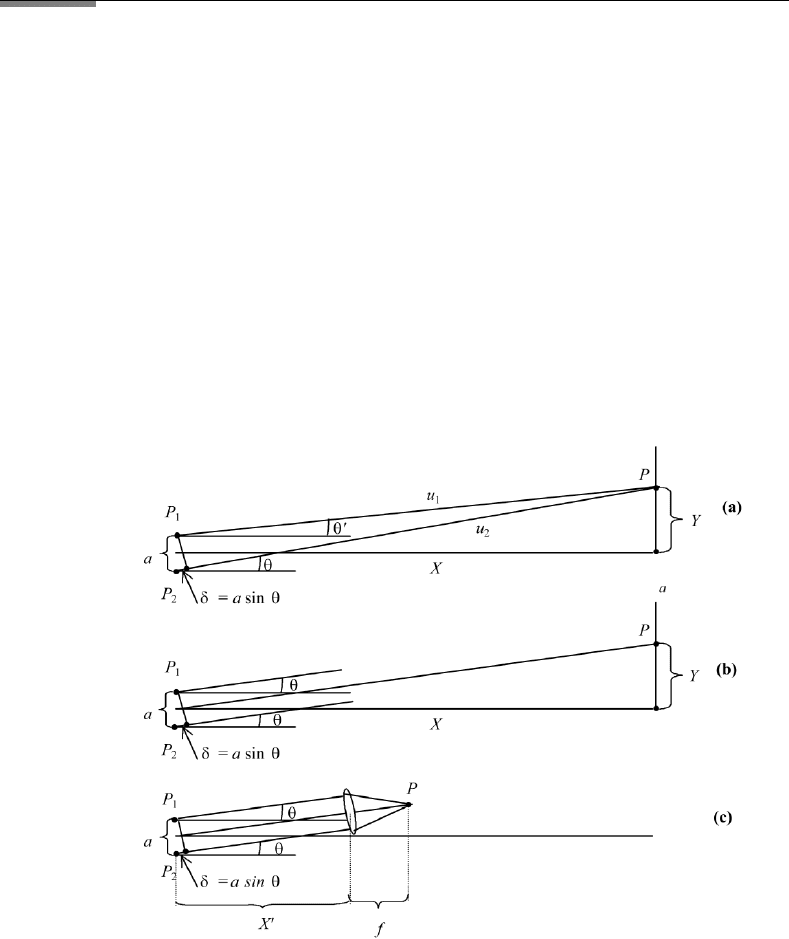
propagating under an angle with respect to each other (see Figure 2.4a). When

we observe the interference pattern at a faraway screen (see Figure 2.4b) the

FIGURE 2.4 Observation of interference pattern generated by two sources. The generated waves

have a constant phase relation: (a) geometry of the experiment with water waves (see also Figure

2.3); (b) Observation at a screen far away from the source; (c) using a lens to reduce the distance

X in (b) to distance X



in (c). In this case only parallel rays meet at one point in the focal plane of

the lens.

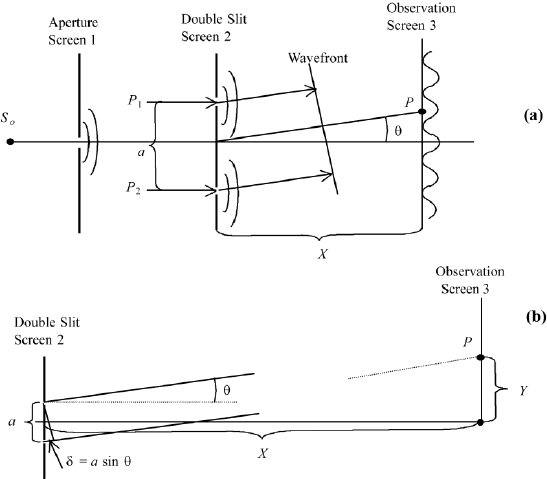
90 2. INTERFERENCE

FIGURE 2.5 Schematic ofYoung’s experiment. Light is emitted by the source S

: (a) according to

Huygen’s principle, the ﬁrst aperture A

produces a spherical wave which generates two spherical

waves with ﬁxed phase relation at P

and P

and produces a fringe pattern; (b) coordinates for the

calculation of the fringe pattern generated by screen 2 and observed on screen 3. The two openings

on screen 2 are separated by a. The distance from screen 2 to screen 3 is X and the coordinate on

screen 3 is Y .

angles θ and θ



are almost equal. We therefore approximate the propagation by

assuming that the two waves move in parallel, and that the optical path difference

δ is the same as it was when moving under an angle. We describe both waves

in the same coordinate system and use for the intensity of their superposition

I  I

[A cos(2πδ/2λ)]

(see Eq. (2.25). In Figure 2.4c we show the observation

in the focal plane of a lens, giving us the opportunity to have the distance between

the experimental setup and the observation screen signiﬁcantly shorter.

2.4.2 Young’s Experiment

The setup of Young’s experiment is schematically shown in Figure 2.5a. The

light from a source S

travels to screen 1, which has a small hole. At the hole, a

spherical wave is created and travels a large distance. The wave arrives at screen

2 as “almost” a plane wave. At two small holes on screen 2, P

and P

, the

incident plane wave is split into two spherical waves. The two spherical waves

travel a large distance and arrive at screen 3 as “almost” plane waves. Their

wavefronts are tilted by a small angle with respect to each other, resulting in

an optical path difference and superposition results in a fringe pattern. In our

2.4. TWO-BEAM WAVEFRONT DIVIDING INTERFEROMETRY

model calculation, we assume that the two monochromatic waves, leaving the

two openings, travel in parallel in the same direction. They have the angle θ with

respect to the symmetry axis and the optical path difference δ (see Figure 2.5),

δ  a sin θ. (2.27)

In the small angle approximation we have δ  aY/X, and obtain the intensity

of the fringes on the observation screen, using Eq. 2.25

I (Y )  I

[cos{(πaY)/(Xλ)}]

. (2.28)

Constructive interference is observed for

δ  Ya/X  0,λ,2λ,.... (2.29)

and destructive interference for

δ  Ya/X  λ/2, 3λ/2, 5λ/2, (2.30)

The graph in FileFig 2.5 shows the intensity forYoung’s experiment, depending

on Y , using the coordinate on the observation screen. One observes that there

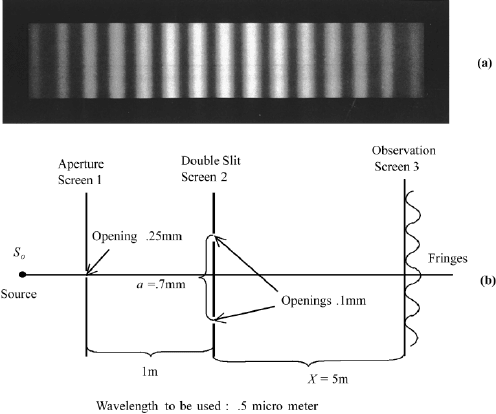
is a maximum at the center. In Figure 2.6, a photograph shows the interference

pattern of Young’s experiment and an experimental setup for its observation.

FIGURE 2.6 (a) Photograph of interference pattern observed with Young’s experiment (from M.

Cagnet, M. Francon, and J.C. Thrierr, Atlas of Optical Phenomena, Springer-Verlag, Heidelberg,

1962); (b) physical dimensions for the observation of fringes inYoung’s experiment, according to

R. Pohl.

2. INTERFERENCE

FileFig 2.5 (I5YOUNGS)

The intensity for Young’s experiment (Eq. (2.28)), is plotted for λ  0.0005 mm,

a  0.4 mm, and X  4000 mm. For this choice of parameters, we see that

the separation of the holes on screen 2 (see Figure 2.5), are three orders of

magnitude larger than the wavelength and four orders of magnitude smaller

than the distance between screens 2 and 3.

I5YOUNGS is only on the CD.

Application 2.5.

1. Change the separation of the source points a to

a and 2a.

2. Change the wavelength λ to

λ and 2λ.

3. Compare the changes of the ratio a/λ to

and 2 times its value.

4. There are no changes if we keep the product (a/λ)(Y/X) constant, where

Y/X is the angle under which we observe the fringes.

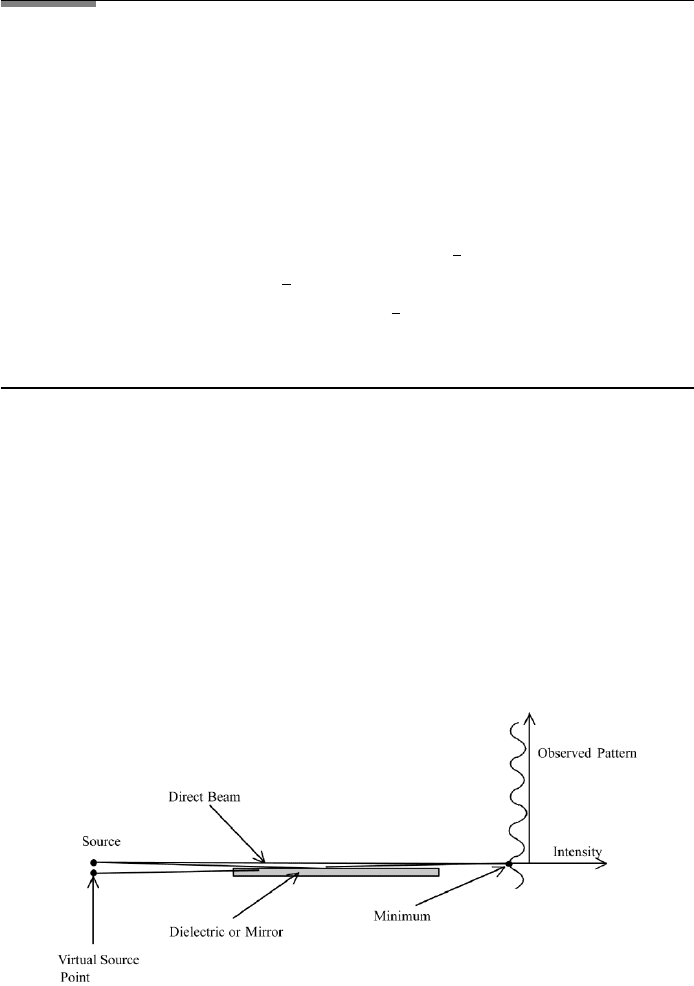
2.4.2.1 Lloyd’s Mirror

In the experiment by Lloyd, interference fringes are produced by using one

mirror. Two parts of the incident wave are superimposed. One part travels directly

from the source to the observation screen, while the other part is incident on the

mirror and is reﬂected under a grazing angle (see Figure 2.7). For the calculation

of the optical path difference δ, we use a virtual source S



at distance a/2 from

the plane of the mirror, but on the “other side” of the mirror. Similarly, as in

Young’s experiment, we have for the optical path difference δ  Ya/X, and

consider the two waves traveling parallel to the observation point. One has to take

into account that one of the two superimposed waves has picked up a phase shift

FIGURE 2.7 Optical schematic for Lloyd’s mirror experiment drawn with exaggerated size of the

angles. One wave from the source travels directly to the observation point; the other is reﬂected

at the mirror. Since the distance of the source from the plane of the mirror is very small the ﬁrst

fringe is about in the plane of the reﬂecting surface. It is a minimum because of the phase shift.

2.4. TWO-BEAM WAVEFRONT DIVIDING INTERFEROMETRY 93

of π upon reﬂection on the mirror. This phase shift appears as π in cos{2π (x/λ−

t/T) + π}, and after superposition, as π/2 in the amplitude factor used for the

intensity. We therefore have

I (Y )  I

[cos{π(Ya/Xλ) + π/2}]

. (2.31)

For interference one has

Ya/X+ λ/2  0,λ,2λ,... or δ  Ya/X  λ/2, 3λ/2, 5λ/2 (2.32)

and for interference

Ya/X+ λ/2  λ/2, 3λ/2, 5λ/2,... or δ  Ya/X  0,λ,2λ... (2.33)

The graph in FileFig 2.6 shows the intensity of Lloyd’s mirror experiment

depending onY, the coordinate on the observation screen. In comparingYoung’s

experiment to Lloyd’s, one has a minimum at the center.

FileFig 2.6 (I6LOYDS)

Intensity of Lloyd’s experiment for λ  0.0005 mm, a  .4 mm, and X 

4000 mm. The “ﬁrst” fringe is dark, that is, a minimum for Y  0, because of

the phase shift upon reﬂection of one of the two waves. The dependence of the

fringes on a and λ are the same as in Young’s experiment.

I6LOYDS is only on the CD.

2.4.2.2 Fresnel’s Double Mirror Experiment

Fresnel’s mirror experiment was originally performed to prove the wavelike

character of light. Even today it is of some interest since the fringes depend on

the tilting angle of the mirrors and may be applied to wavelengths as short as

Xrays. The wavefront of the spherical wave, emerging from the source, is divided

by two mirrors, which are tilted by a very small angle β (Figure 2.8a). Each part

of the incident wave is reﬂected, and the two wavefronts are tilted by the angle

β. The superposition produces the fringe pattern. In our model description we

consider the waves at the faraway observation screen as parallel. The optical

path difference is the same as calculated when the two waves travel under the

small angle β. Making these assumptions, the optical path difference is obtained

using the two virtual source points S



and S



at distance a (see Figure 2.8a).

It is similarly done as for Young’s experiment (Figure 2.8b). The distance from

the virtual sources to the observation screen is c + f  X, and the optical path

difference δ  a(Y/X) of the light reﬂected by the two Fresnel mirrors is

δ  (Y 2b sin β)/(c + f ). (2.34)

94 2. INTERFERENCE

FIGURE 2.8 (a) and (b) are for Fresnel’s mirror experiment. S is the source, S



and S



are virtual

source points. They are separated by a and have a tilting angle β. The coordinate on the observation

screen is Y . The relation a  2b sin β is obtained by associating “one b” with one mirror and the

“other b” with the other mirror, and remembering that light is reﬂected by 2β if the mirror is tilted

by β; (c) approximate treatment of Fresnel’s mirror experiment similar to Young’s experiment.

The intensity is

I (Y )  I

[cos{(πY2b sin β)/[(c + f )λ]}]

, (2.35)

and for constructive interference

δ  Y 2b sin β/(c + f )  0,λ,2λ,... (2.36)

and destructive interference

δ  Y 2b sin β/(c + f )  λ/2, 3λ/2, 5λ/2,... (2.37)

The graph in FileFig 2.7 shows the intensity of Fresnel’s double mirror experi-

ment with a maximum at the center, since both waves are reﬂected on a mirror

2.4. TWO-BEAM WAVEFRONT DIVIDING INTERFEROMETRY 95

and pick up a phase shift π. In FileFig 8 we compare the intensities of Young’s,

Lloyd’s, and Fresnel’s double mirror experiments and see the role the phase shift

plays.

FileFig 2.7 (I7FREMIRS)

Intensity of Fresnel’s double mirror experiment, Eq. (2.35) for λ  0.0005 mm,

b  1000 mm, f  5000 mm, and for the angle β  0.0002.

I7FREMIRS is only on the CD.

Application 2.7.

1. How is the pattern changing when changing λ. How much must λ be changed

to double the separation of the maxima or to make them one half.

2. How is the pattern changing when changing β. How much must β be changed

to double the separation of the maxima or to make them one half.

3. What angle β has to be chosen to have the maxima separated by 500 microns

when using Xrays of 500 Angstrom (1

Ais10

−10

m).

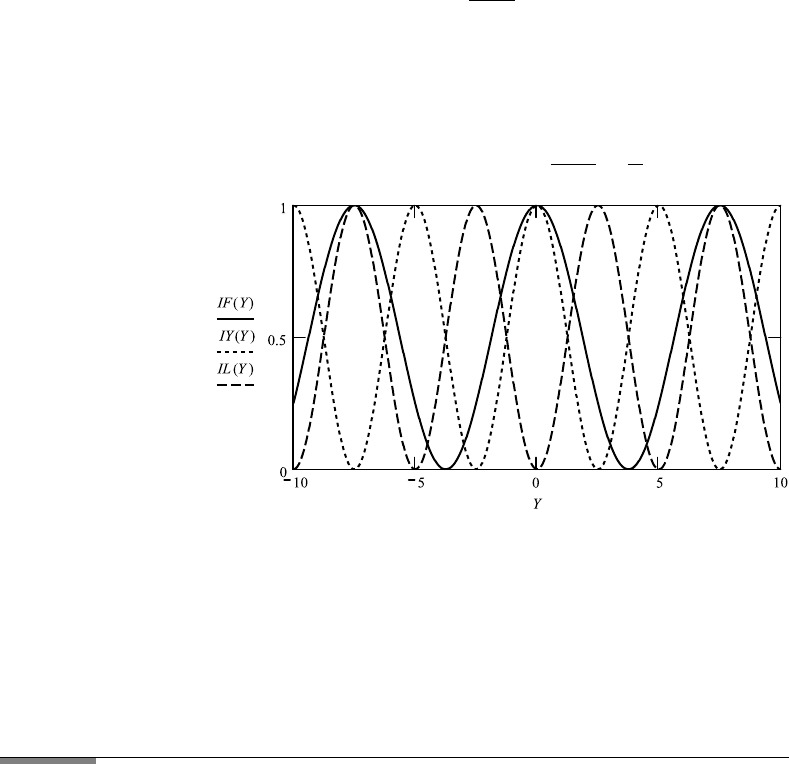
FileFig 2.8 (I8FRYOLOS)

Comparison of experiments by Young, Lloyd, and Fresnel. For the choice of

parameters, we see that the separation of the “sources” are three orders of

magnitude larger than the wavelength, and four orders of magnitude smaller

than the distance X between experimental setup and observation screen.

I8FRYOLOS

Fresnel’s Mirror, Young’s Double Slit, and Lloyd’s Mirror

1. Fresnel’s mirror

Y , c, f , b, and λ in mm, β in rad; c is about b for calculation of X  c +f .

All lengths in mm.

Con : 1 λ deﬁned above

graph

b : 1000 f : 5000 c : b cos(β) β ≡ .0002 Y :−10, −9.99 ...10

IF(Y ): Con · cos



π ·

Y · 2

c+f

· sin(β)



96 2. INTERFERENCE

2. Young’s experiment

a ≡ .4 X ≡ 4000

IY(Y ): Con · cos



π ·

Y · a

λ · X



λ ≡ .0005

3. Lloyd’s mirror

Same as Young, phase term is added.

IL(Y ): Con · cos



π ·

Y · a

λ · X



We see that at Y  0 Young has a maximum, Lloyd a minimum. For Young

and Lloyd: the position of maxima are changed by changing d and λ; X is

considered ﬁxed. For Fresnel, a, b are ﬁxed; position of fringes changes with

β and λ.

2.5 TWO-BEAM AMPLITUDE DIVIDING

INTERFEROMETRY

2.5.1 Model Description for Amplitude Division

We again assume a monochromatic wave incident on the experimental setup,

propagating in the x direction, vibrating in the y direction, and having a large

lateral extension in the z direction.

The incident wave is incident on a beam splitter. One part is reﬂected and the

other part is transmitted. One or both parts are manipulated in the experimental

setup to pass through a beamsplitter a second time. Fractions of each part are

superimposed and travel parallel to the observation screen.