Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple

Подождите немного. Документ загружается.

76 1. GEOMETRICAL OPTICS

matrix, the light may pass through many round trips and no light will escape.

One calls such a resonator stable, and the condition for stability is where the

magnitudes of the eigenvalues are equal to 1.

|λ

||λ

|1. (1.116)

We may write for Eq. (1.114),

 (2g

− 1) + [(2g

− 1)

− 1]

1/2

(1.117)

 (2g

− 1) + i[1 − (2g

− 1)

]

1/2

. (1.118)

The real and imaginary parts of Eq. (1.118) must be on a circle of radius 1; that is,

|(2g

− 1)|≤1, or 0 ≤ g

≤ 1. (1.119)

in agreement with the imaginary part and plotted in FileFig 1.32.

In FileFig 1.33 we show a repetition of the calculations, starting from the

ﬁve matrices of the cavity in Eq. (1.111), but now in terms of r

, r

, and d.In

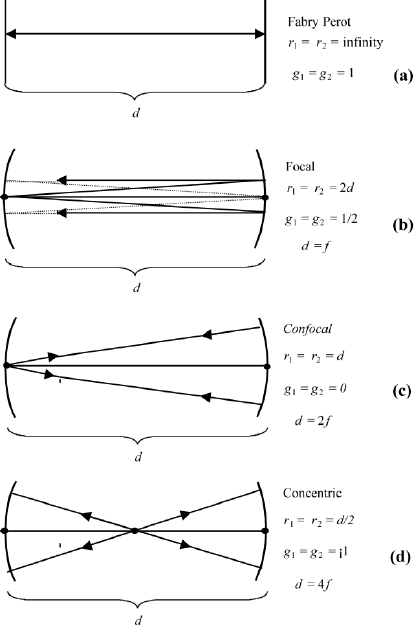
Figure 1.33, we show schematics of the Fabry–Perot, a focal, a confocal and a

spherical cavity for values of the parameters r

, r

, and d, and also of g

and g

For both representations one ﬁnds that the absolute values of the eigenvalues λ

and λ

are always 1.

FileFig 1.33 (G33RESCY)

Calculation of the eigenvalues of the cavity with two reﬂecting mirrors using r

, and d. Numerical calculation with r

 1, r

 1, and d  2.

G33RESCY is only on the CD.

Application 1.33. Use the values of the parameters r

, r

, and d for the Fabry–

Perot, focal, confocal, and spherical cavities, and ﬁnd that all are stable cavities.

1.10. MATRICES FOR A REFLECTING CAVITY AND THE EIGENVALUE PROBLEM 77

FIGURE 1.33 Schematic of light path for four cavities with different values of radii of curvature

and length of cavity. The corresponding valuesof g

and g

are indicated: (a) Fabry–Perot; (b) focal;

CHAPTER

Interference

2.1 INTRODUCTION

In Chapter 1 we described image formation by light, using our model which states

that light propagates along straight lines and utilizes the laws of reﬂection and

refraction. We now consider the wave nature of light. In the famous experiment

by Thomas Young, one observes on a screen an interference pattern, consisting

of bright and not so bright stripes of light. The interpretation of an interference

pattern was done by using an analogy to water waves. However, the water wave

pattern is observed as an amplitude interference pattern whereas the superpo-

sition of light waves, also generated as an amplitude pattern, is observed as an

intensity pattern. Historically, Newton associated the light beams of geometrical

optics with a stream of particles and some scientists attacked Young in his time,

saying that he was diminishing Newton’s work. Today we know that light is an

electromagnetic wave but, in a complementary way, light is also described by

quantum mechanics as an assembly of particles.

In this chapter we use a model for the description of interference phenomena.

We assume that there is always one incident wave when two- or more beam in-

terferometry is discussed. After one has taken into account what happens in the

experimental setup, the waves leaving the setup appear superimposed. The inter-

ference pattern is produced with ﬁnite optical path differences. The calculation

of the optical path difference and the interpretation of the resulting interference

pattern are the main subjects of this chapter. The process of splitting the inci-

dent wave into parts involves diffraction, which we neglect in this chapter as a

secondary effect and discuss in detail in Chapter 3.

In this chapter we use for the incident wave one harmonic wave, a solution of

the scalar wave equation, which is written in Cartesian coordinates as

∂

u/∂x

+ ∂

u/∂y

+ ∂

u/∂z

 (1/v)

∂

u/∂t

, (2.1)

80 2. INTERFERENCE

where v is the phase velocity of light in the medium with refractive index n,

related to the speed of light c in vacuum as v  c/n. The scalar wave equation

follows from Maxwell’s theory. It may also be written in spherical coordinates

∇

u + k

u  0, (2.2)

where ∇ is the differential operator in spherical coordinates, k  2π/λ, and λ

is the wavelength of the light. A simple solution of this equation is a spherical

wave of the type (e

ikr

)/r, where r is the distance from the origin to the ob-

servation point. The spherical wave propagates from its origin in all directions

and its intensity is attenuated by 1/r

. We consider such spherical waves only

conceptually and approximate them at a large distance by plane waves.

The differential equation of the scalar wave equation is linear and superposi-

tion of solutions of the differential equation will again result in a solution. This

is part of the superposition principle. In this chapter we only need the superpo-

sition of a number of monochromatic waves, each of frequency ν, to result in a

monochromatic wave having the same frequency ν.

For our model description we use some results from Maxwell’s theory for

quantitative expressions of the reﬂection and transmission coefﬁcients of mate-

rials contained in Fresnel’s formulas. In particular, we use the results that waves

pick up a phase jump of π, when reﬂected at an optically denser medium, and

that they travel in the optically denser medium with wavelength λ/n, where n is

the index of refraction. The intensity is calculated either as the time average of

the square of the amplitude or the square of the absolute value of the complex

representation and may be normalized with an arbitrary constant.

2.2 HARMONIC WAVES

The solution of the scalar wave equation, (Eq. (2.1)), is a function, depending on

the space coordinates x, y, z and the time t . In addition, there may be an arbitrary

phase factor. We consider harmonic waves in vacuum and in an isotropic and

nonconducting medium of index n. However, in most cases, we only need waves

depending on one space coordinate and time. We describe the transverse waves

by vibrating in the u direction and moving in the x direction, having wavelength

λ and time period T .

u  A cos[2π(x/λ − t/T +φ)]. (2.3)

The amplitude u of the wave varies in the x direction, A is the magnitude of

the wave, and φ is a phase constant. The ﬁrst graph of FileFig 2.1 shows the

amplitude u, depending on the space coordinate x for three time instances t and

three phase constants. The second graph shows the dependence on time for three

points in space and three phase constants. The magnitudes A

to A

and B

2.2. HARMONIC WAVES 81

FIGURE 2.1 Change of wavelength as the wave enters and leaves a dielectric medium.

have been assumed to have the same value, and the three phase constants

to φ

and 

to 

are assumed to be different. Comparing the graphs, one

observes equivalence of the dependence of the cosine function on x/λ and t/T.

Changing the range of variable from x to t, the family of curves depending on x

is similar to the one depending on t.

We may modify x/λ and t/T in such a way that they contain phase constants.

Then, in the “net” expression cos[2π (x/λ−t/T +φ)] we can not distinguish if φ

belongs to the space part or the time part. We show below that for our discussions

on interference we do not need the time dependence and it is eliminated.

The product of the frequency ν and wavelength λ/n is equal to the phase

velocity v  ω/k of the wave propagating in the medium of refractive index n.

The angular frequency ω  2πν, and the wave vector k  2πn/λ, where λ is

the wavelength in vacuum. We may then write Eq. (2.3) as

u  A cos(kx − ωt) (2.4)

u  A cos k(x − (ω/k)t)  A cos k(x − vt).

The phase velocity in vacuum is c, and in an isotropic medium with refractive

index n it is c/n. The wavelength of “free space” λ is reduced in the medium to

λ/n (see Figure 2.1).

FileFig 2.1 (I1COSWS)

Cosine functions depending on space and time coordinate and one additional

phase constant. Graphs are shown for cosine functions depending on the space

coordinates for three time instances. This may be interpreted as graphs of the

82 2. INTERFERENCE

same wave at threeconsecutive snapshots. Graphs are shown for cosine functions

depending on the time coordinates for three points in space.

I1COSWS is only on the CD.

Application 2.1.

1. One may change the phase φ and the space coordinate and choose both so

there is no resulting change in the graph. Choose φ  2,4,6.

2. One may change the phase φ and the time coordinate and choose both so

there is no resulting change in the graph. Choose φ  2,4,6.

3. Change φ in such a way that there is a shift to smaller values of the position

coordinate.

4. Change φ in such a way that there is a shift to larger values of the time

coordinate.

2.3 SUPERPOSITION OF HARMONIC WAVES

2.3.1 Superposition of Two Waves Depending on Space and

Time Coordinates

We describe the interference of two waves in a simple way, using the superpo-

sition of two harmonic waves u1 and u2. Both waves will propagate in the x

direction and vibrate in the y direction.

 A cos 2π[x/λ − t/T] u

 A cos 2π[(x − δ)/λ − t/T]. (2.5)

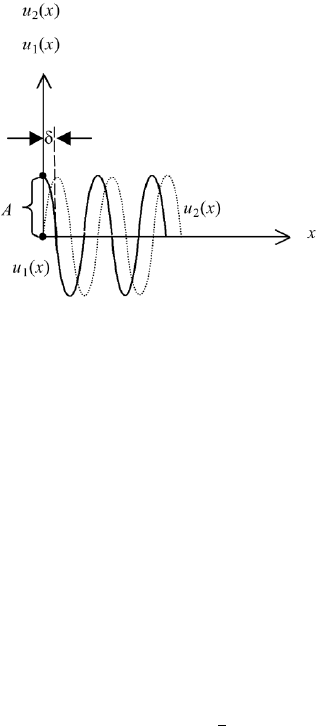
We assume that the two waves have an optical path difference δ.At time instance

t  0, the wave u

has its ﬁrst maximum at x  0, and u

at x  δ (Figure 2.2).

Adding u

and u

we have

u  u

+ u

 A cos 2π[x/λ − t/T] + A cos 2π[(x −δ)/λ − t/T]. (2.6)

Using

cos(α) +cos(β)  2 cos{(α − β)/2}cos (α + β)/2 (2.7)

we get

u  [2A cos{2π(δ/2)/λ}][cos{2π(x/λ − t/T) − 2π(δ/2)/λ}]. (2.8)

In FileFig 2.2 we show graphs of the square of Eq. (2.8) for the same time instant

and wavelength λ. We choose a number of optical path differences δ

 0,

 0.1, δ

 0.2, δ

 0.3, δ

 0.4, δ

 0.5, corresponding to the ratios

of the optical path difference to the wavelength between 0 and

. One observes

that the height of the maxima decreases with increasing δ

to δ

, and shifts to

larger values of x.

2.3. SUPERPOSITION OF HARMONIC WAVES 83

FIGURE 2.2 Two waves with magnitude A and wavelength λ.Wehaveu

 A for x  0 and

 A for x  δ.

We nowdiscuss the twofactors of Eq. (2.8). The ﬁrst factor 2A cos{2π (δ/2)/λ}

depends on δ and λ, but not on x and t. One obtains for δ equal to 0 or a multiple

integer of the wavelength

[2A cos{2π(δ/2)/λ}]

is 4A

(2.9)

and for δ equal to a multiple of half a wavelength

[2A cos{2π(δ/2)/λ}]

is 0. (2.10)

The ﬁrst factor in Eq. (2.8) may be called the amplitude factor and is used for

characterization of the interference maxima and minima.

One has

maxima for δ  mλ, where m is 0 or an integer (2.11)

minima for δ  mλ, where m is

plus an integer (2.12)

and m is called the order of interference.

The second factor is a time-dependent cosine wave with a phase constant

depending on δ and λ. For the description of the interference pattern this factor

is averaged over time and results in a constant, which may be factored out and

included in the normalization constant (see below).

In Figure 2.3 we show schematically the interference of two water waves

with a ﬁxed phase relation. When the interference factor is zero one has minima,

indicated by white strips. They do not depend on time. The maxima oscillate and

appear and disappear along the line in the observable direction.

Maxima and minima are shown in FileFig 2.3 as 3-D graphs. The maxima

are shown for δ  λ, and in the second graph, for δ  λ/2, there is just one

minimum. The maxima show the time dependence of the second factor for each

of the space coordinates. One can estimate that a time average will result in half

the maximum value. The minimum is zero. It is zero for all time.

84 2. INTERFERENCE

FIGURE 2.3 Schematic of the interference pattern produced by two sources vibrating in phase. At

the crossing of the lines, the amplitudes of the waves of both sources are the same and adding. Taking

the time dependence into account, the magnitude changes between maximum and minimum.

These are the maxima when considering light. Between the maxima we indicate the two lines

corresponding to the minima. Along these lines the amplitude of the two waves compensate each

other; their sum is zero for all times.

FileFig 2.2 (I2COSSUPS)

Graphs of the superposition of two cosine waves with wavelength λ  1, for

a number of optical path differences δ

 0, δ

 0.1, δ

 0.2, δ

 0.3,

 0.4, δ

 0.5 corresponding to ratios of the optical path difference to the

wavelength between 0 and

I2COSSUPS is only on the CD.

Application 2.2.

1. Extend the range of the optical path differences of the six graphs from

wavelength to 1 wavelength, and then from 1 wavelength to

wavelength

and indicate in a list when there is repetition.

2. Make a graph of y  cos{2π(δ/2)/λ}for ﬁxed λ as function of δ and make a

list of the δ values for minima and maxima. Compare with a list of δ/λ values.

FileFig 2.3 (I3COSGRA)

3-D demonstration of the superposition of two waves for δ/λ  1 corresponding

to a maximum, and δ/λ  0.5 corresponding to a minimum. In the graph of the

maximum, the amplitude changes in time for a speciﬁc spot in space between

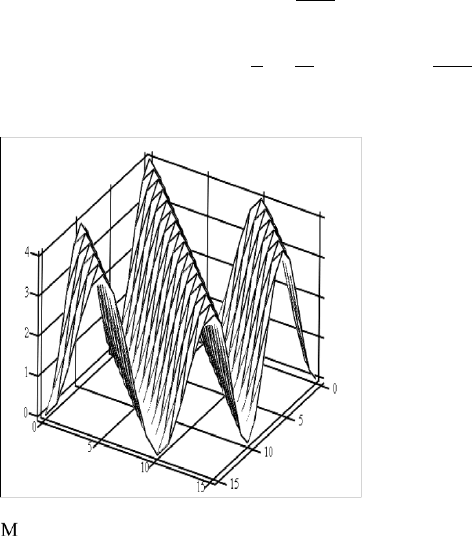
2.3. SUPERPOSITION OF HARMONIC WAVES 85

0 and (2A)

, and one can estimate that the time average will be half of it. The

graph of the minimum is zero for all time and space values.

I3COSGRA

Superposition of Two Cosine Waves

One wave has optical path difference δ with respect to the other. The sum is

squared to result in the intensity. We are looking at them time dependence; the

graphs are plots in space x and time t. Period T , path difference δ, wavelength λ.

1. Graph for optical path difference corresponding to a maximum

λ : 1 A : 1

N : 40 i : 0 ...N j : 0 ...N

:−.2 + .05 · it1

:−.2 + .05 · j

uc(x, t1) :



2 ·A · cos



2 ·π ·



δ1

2 ·λ





cos



2 ·π ·



−



− 2 ·π ·



δ1

2 ·λ



i,j

: uc



,t1



δ1 ≡ 1 T ≡ 1 t1 ≡ .1.

2. Graph for optical path difference corresponding to a minimum

N : 40

i : 0 ...N j : 0 ...N

:−.2 + .04 · it1

:−.2 + .02 · jδ2 ≡ .5

86 2. INTERFERENCE

ud(xx, t1) :



2 ·A · cos



2 ·π ·



δ2

2 ·λ





cos



2 ·π ·



−



− 2 ·π ·



δ2

2 ·λ



i,j

: ud



,t1



t1 ≡ .1 T ≡ 1.

Application 2.3. One may change the wavelength λ such that for δ1/λ one gets

minima, and for δ2/λ one gets maxima.

2.3.2 Intensities

The interference pattern of water waves is an amplitude pattern. We may observe

minima and maxima with respect to the level of the undisturbed water surface.

The interference pattern of light shows intensity minima as dark spots in space

and maxima as bright spots. An amplitude pattern shows negative amplitudes,

but an intensity pattern has only positive or zero values. The amplitude pattern

has to be considered ﬁrst; it produces interference. Then we have to obtain the

intensity pattern. We compare the intensity pattern to observations.

For the square of the amplitude of equation (2.8) we have

 [2A cos{2π(δ/2)/λ}]

[cos{2π(x/λ − t/T) − 2π(δ/2)/λ}]

(2.13)

In Section 2.1 we mentioned that for the intensity we use either the time average

of the square of the amplitude or the square of the absolute value, when using

complex notation. In this section we compare these two calculations.