Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple

Подождите немного. Документ загружается.

2.5. TWO-BEAM AMPLITUDE DIVIDING INTERFEROMETRY

The splitting of amplitude division is different from the splitting discussed for

wavefront division. The two waves after wavefront division travel under an angle.

After amplitude division, it can be arranged, that both parts travel in parallel in

the same direction. The difference between wavefront and amplitude division

is related to energy conservation. It is impossible to superimpose two beams in

such a way that all the light travels in one direction.

The interference pattern is observed at a faraway screen, and the intensity of the

interference pattern is given as I  I

[A cos(2πδ/2λ)]

(see Eq. (2.25)), where

δ is the optical path difference. The observation may be done in the focal plane

of a lens, making the actual distance between the experiment and observation

screen much shorter.

2.5.2 Plane Parallel Plate

The interference on a plane parallel plate is the model for the description of

interference on thin ﬁlms, used in various technologies such as coating lenses or

mirrors for use with Xrays.

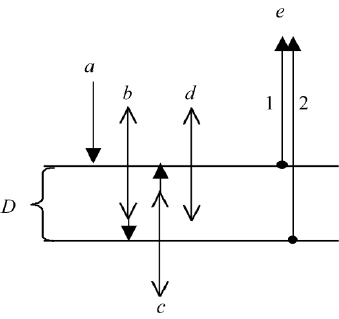
We consider light incident on a plane parallel plate of glass of thickness D

and index of refraction n>1, and assume n  1 for the media outside the plate.

The incident light, shown in Figure 2.9 at (a), is split at the ﬁrst interface into a

reﬂected and transmitted part (shown at (b)). The transmitted light is reﬂected

and transmitted at the second interface (shown at (c)) and the reﬂected light is

again reﬂected and transmitted at the ﬁrst interface (shown at (d)). We use for

further consideration only the light reﬂected from the ﬁrst interface (shown as

(1)) and the light reﬂected at the second interface, and then transmitted through

the ﬁrst interface (shown as (2)).

FIGURE 2.9 Plane parallel plate at thickness D and refractive index n; (a) incident light; (b) split-

ting at ﬁrst interface; (c) splitting at second interface, (d) splitting at ﬁrst interface again; (e) the

two waves, (1) from b and (2) from c superimposed to generate the interference fringes.

98 2. INTERFERENCE

The path difference between the waves (1) and (2) is

δ  2Dn. (2.38)

Both waves (1) and (2) travel in the same direction, and (1) picks up a phase shift

of π when reﬂected at the ﬁrst interface. For the calculation of the optical path

difference we have to multiply 2D by n. In addition, we have to take into account

that the reﬂection on the denser medium, that is, the glass, for wave (1) results

in a phase shift of π, equivalent to λ/2. The optical path difference is then

δ  2Dn + λ/2, (2.39)

where λ is the wavelength outside of the plate. One has for the intensity

I  I

[cos{π(2Dn + λ/2)/λ}]

(2.40)

or equivalently

I  I

[cos{π(2Dn)/λ + π/2}]

. (2.41)

We have for constructive interference

δ  2Dn + λ/2  0,λ,2λ, ... (2.42)

2Dn  λ/2, 3/2λ, 5/2λ, ... (2.43)

and for destructive interference

δ  2Dn + λ/2  λ/2, 3λ/2, 5λ/2,... (2.44)

2Dn  λ, 2λ, 3λ,.... (2.45)

We see that the appearance of maxima and minima depends on the thickness and

the index of refraction of the plane parallel plate. Maxima are obtained for integer

numbers of half a wavelength, minima for integer numbers of a wavelength. One

may observe the interference pattern on a plane parallel plate by looking at a

soap bubble. The ﬁlm of the bubble is curved, but equally thick over a small

area. The colored light we see is produced by individual interference of different

wavelengths on the thin ﬁlm of equal thickness.

The ﬁrst graph in FileFig 2.9 shows the dependence of the fringes on the

thickness of the ﬁlm for ﬁxed wavelength λ and refractive index n  1.5. The

second graph shows the dependence on wavelength for ﬁxed thickness D  0.05

and n  1.5. One observes that there is no interference on the thin ﬁlm when

the wavelength gets too large.

2.5. TWO-BEAM AMPLITUDE DIVIDING INTERFEROMETRY 99

FileFig 2.9 (I9PLANS)

The intensity of two-beam interference on a plane parallel plate of index n2 in

medium with index n1  1. The graphs shown are: (i) Dependence on thickness

for ﬁxed wavelength λ  0.0005 and n  1.5; (ii) Dependence on wavelength

for ﬁxed thickness D  0.05 and n  1.5.

I9PLANS is only on the CD.

Application 2.9.

1. Modify the formula to I(D) {cos(2π Dn/λ + λ/2)}

, for the case that the

index of the outside medium is not 1.

2. Consider the following conﬁgurations:

a. an air gap between glass media (n  1.5).

b. a water ﬁlm (n  1.33) on glass, and incident light in medium n  1.

c. a water ﬁlm on glass and incident light in glass.

Using a graph for ﬁxed D, start counting maxima at any particular maxima

on the graph. Read from the graph the difference in D between, for example,

5 maxima. Recalculate the wavelength using the value of n.

3. When the wavelength exceeds the thickness of the plate, the last fringe is

observed for a value of λ, depending on D and n. Find the formula.

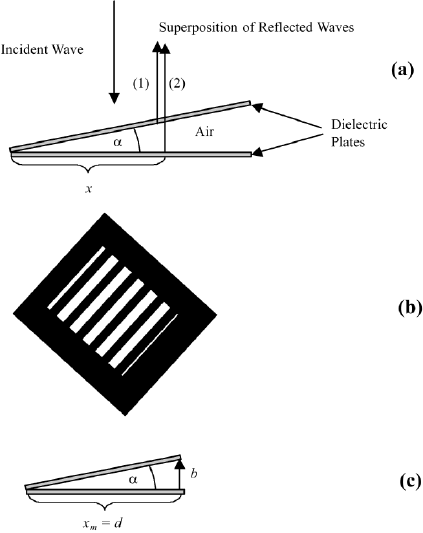
2.5.2.1 Wedge-Shaped Air Gap

We consider two glass plates in air with one on top of the other. With a thin

object, we produce a wedge shaped air gap of small angle α. As we did for the

plane parallel plate, we calculate the optical path difference for the two waves

(1) and (2), on the two interfaces of the air gap (Figure 2.10a (side view)). The

optical path difference is

δ  2x tan α, (2.46)

where α is the angle of the wedge and x the distance from the point where the

plates are touching. The wave reﬂected at the lower plate picks up a phase shift

of π, equivalent to λ/2. For the two waves (1) and (2) one has constructive

interference

2x tan α + λ/2  0,λ,2λ, 3λ,...,mλ (2.47)

and destructive interference

2x tan α + λ/2  1/2λ, 3/2λ, 5/2λ,...,(m + 1/2)λ. (2.48)

The width D



 x tan α at the mth maximum is



 (m − 1/2)λ/2, (2.49)

100 2. INTERFERENCE

FIGURE 2.10 (a) Optical diagram for a wedge-shaped gap of air between two dielectric glass

plates (microscope slides). The gap angle α is assumed to be small. As x increases, the optical

path difference between waves (1) and (2) also increases, resulting in an interference pattern;

(b) schematic of fringe pattern observed with optical plates ﬂat to a fraction of a wavelength λ;

 d and tan α  b/d.

where m  1, 2, 3,...,and for destructive interference



 mλ/2, (2.50)

where m  0, 1, 2, 3,....For the intensity we have

I  I

[cos{(π2x tan α)/λ + π/2}]

. (2.51)

Interference produced by a wedge-shaped air gap is used to determine the uni-

formity of a polishing job, schematically shown in Figure 2.10b. A ﬂat plate is

used to produce an air gap over a plate, which has been polished. If the maxima

and minima are not straight lines, the width of the air gap varies. Deviations of

a fraction of a wavelength can be detected.

One can make a simple experiment with two microscope slides and a plastic

ﬁlm. The ﬁlm is placed at the end of one slide, and a wedge of length approx-

imately 5 cm may be produced with the other microscope slide. Observation

of fringes and their corresponding distances makes it possible to determine the

thickness of the plastic ﬁlm.

2.5. TWO-BEAM AMPLITUDE DIVIDING INTERFEROMETRY 101

FileFig 2.10 (I10WEDGES)

The intensity for interference depending on the distance x, of a wedge of α 

0.002 rad and λ  0.0005 mm. The distance between the maxima is a constant,

given as λ/(2 tan α). We have also plotted the height depending on the length x

for angle α, using a scaling factor a. The ﬁrst fringe is a minimum, as observed

for Lloyd’s mirror, because the thickness at origin D



 0.

I10WEDGES is only on the CD.

Application 2.10.

1. From the condition of constructive interference (2x tan α + λ/2  0, λ,

2λ,...,mλ), show that we have for the difference x

 x

m+1

− x



λ/(2 tan α), where x

is the x coordinate at the mth fringe.

2. Since y

/x

 tan α, where y

is the height difference of the plates

between fringes, show that we have y

 λ/2.

3. Assume we observe M fringes over the length x

 d and want to determine

the height b of the gap at that point (see Fig. 2.10a. Since b/d  tan α 

(λ/2)/x

, show that we have b  (λ/2)M.

4. Recalculation of α: produce a graph with λ  .00054 and α  .0023. Find

the x coordinate at the 23rd fringe and use for the y coordinate y  (λ/2)23.

Calculate α and compare with input data.

5. Modify the determination of the height at some chosen point x

for a water

ﬁlm (n  1.33) between glass plates (n  1.5).

2.5.2.2 Newton’s Rings

A circular interference pattern may be observed if a spherical surface is placed

on a ﬂat surface. The ring pattern is called “Newton’s rings” and may be used

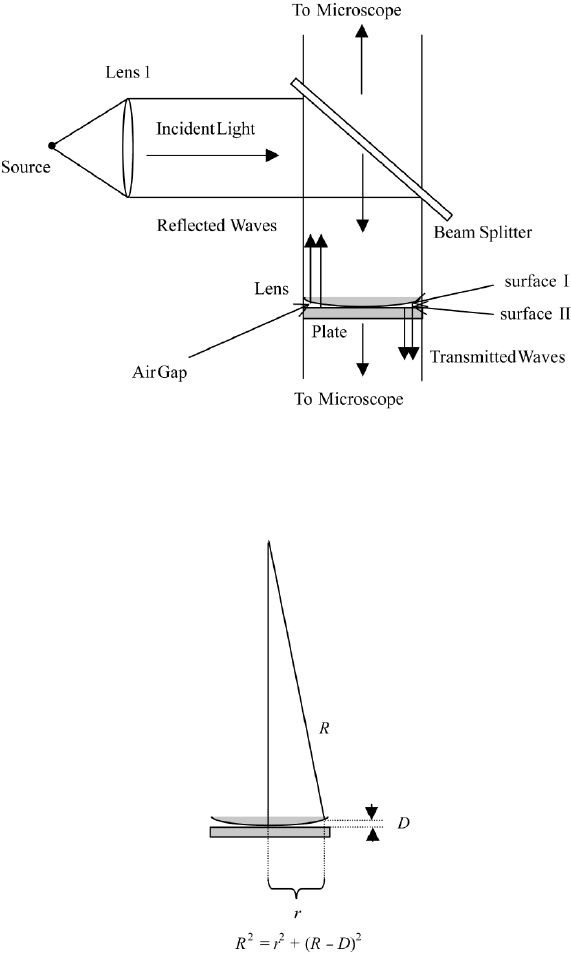
to determine the radius of curvature of the spherical surface. An experimental

setup is shown in Figure 2.11.

A plane convex lens touches a plane parallel plate and an air gap of width D

is formed between the lens and the plate. We call the radius of curvature of the

spherical surface R and the radius of the rings of the pattern r (Figure 2.12). One

has the relation

 r

+ (R − D)

. (2.52)

After solving a quadratic equation, we have for D(r)

D(r)  R −



− r

). (2.53)

The transmitted intensity is

I (r)  I

{cos(π2D(r)/λ)}

. (2.54)

102 2. INTERFERENCE

FIGURE 2.11 Experimental setup for the observation of Newton’s rings. Light is made parallel

by lens 1 and is reﬂected by the beam splitter to the lens-plate assembly. Reﬂected light from

surfaces I and II travels to microscope 1 for observation of fringes in reﬂection. Transmitted light

from surfaces I and II travels to microscope 2 for observation of the tranmission fringes.

FIGURE 2.12 Coordinates for the calculation of the optical path difference D between rays from

surfaces I and II.

In addition the reﬂected intensity has the term π/2 because of the reﬂection on

the plane parallel plate of refractive index larger than 1,

I (r)  I

{cos(π2D(r)/λ + π/2)}

. (2.55)

2.5. TWO-BEAM AMPLITUDE DIVIDING INTERFEROMETRY 103

FIGURE 2.13 Newton’s rings observed: (a) using transmitted light; (b) using reﬂected light

(from M. Cagnet, M. Francon, and J.C. Thrierr, Atlas of Optical Phenomena, Springer-Verlag,

Heidelberg, 1962).

For the reﬂected intensities, one has for constructive interference

δ  D(r) + λ/2  0,λ,2λ,..., (2.56)

and for destructive interference

δ  D(r) + λ/2  λ/2, 3λ/2, 5λ/2,.... (2.57)

For the transmitted intensities one has similar expressions without the λ/2 term.

At the center of the plates, at D  0, one has from Eq. (2.55) for reﬂected light

zero intensity; in other words, we should observe a dark spot, shown in Figure

2.13a. For transmitted light, Eq. (2.54) predicts a bright spot, shown in Figure

2.13b.

FileFig 2.11 (I11NEWTONS)

Intensity for Newton’s rings in transmission and reﬂection depending on the

radius r around the center, for λ  0.0005 mm and R  2000 mm.

I11NEWTONS is only on the CD.

Application 2.11. Recalculation of R:

1. Show that we have for the mth ring (fringe) a height in the air gap of mλ/2.

2. Show that we then have to use (mλ/2 − R)

 R

− r

for the calculation

of R, assuming that we have read r

from the graph.

2.5.3 Michelson Interferometer and Heidinger and Fizeau

Fringes

2.5.3.1 Michelson Interferometer and Normal Incidence

In 1880, Albert Michelson used the interferometer, named after him, for his

famous experiments to show that there is no ether. Today most infrared spec-

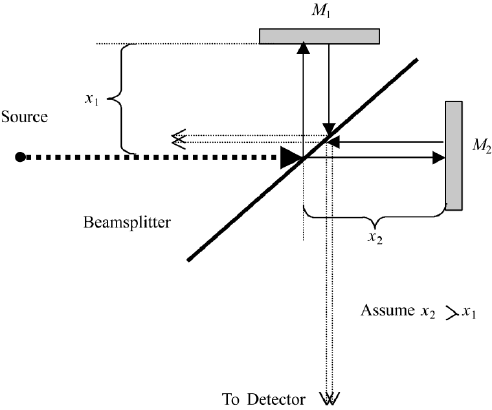
104 2. INTERFERENCE

FIGURE 2.14 The Michelson interferometer with arms of unequal lenght x

and x

in the same

medium.

trometers use the Michelson interferometer to obtain an interferogram and the

application of the Fourier transform produces the desired spectrum. Chapter 9

discusses Fourier transformation and spectroscopy. In Figure 2.14 we show a

schematic of a Michelson interferometer. The amplitude of the incident beam is

partly reﬂected under an angle of 90

◦

toward mirror M

, and partly transmitted

in the direction to mirror M

. The beam splitter may be a plane parallel plate,

and the reﬂection and transmission properties of such a plate are discussed be-

low, including all multiple reﬂections. Here we use an idealized beamsplitter

and assume that 50% of the incident light will be reﬂected, that 50% will be

transmitted, and no phase shift will be introduced.

The reﬂected wave travels to mirror M

, where it is reﬂected and travels back

to the beam splitter for a “second splitting.” It has traveled the distance 2x1

between mirror and beam splitter. We call the transmitted part (1), and note

that the reﬂected part travels back to the source. Similarly, the transmitted wave

travels to M

, is there reﬂected, and travels to the beam splitter for a second

splitting. It has traveled the distance 2x2 and we call the reﬂected part (2); the

transmitted part travels back to the source. Parts (1) and (2) are superimposed

and travel to the detector. If the distances 2x1 and 2x2 are not the same, we have

an optical path difference between (1) and (2) of

δ  2D  2(x

− x

), (2.58)

where we assume that x

. Constructive interference is obtained for

δ  mλ (2.59)

2.5. TWO-BEAM AMPLITUDE DIVIDING INTERFEROMETRY 105

and destructive interference for

δ 



m +



λ, (2.60)

where m  0, 1, 2, 3.

The intensity of interference is obtained as

I  4A

cos

(π2D/λ). (2.61)

The Michelson interferometer was originally designed to perform exact length

measurements. Some time ago, it was used for a now outdated procedure to

deﬁne the length of the meter by using

Kr emission.

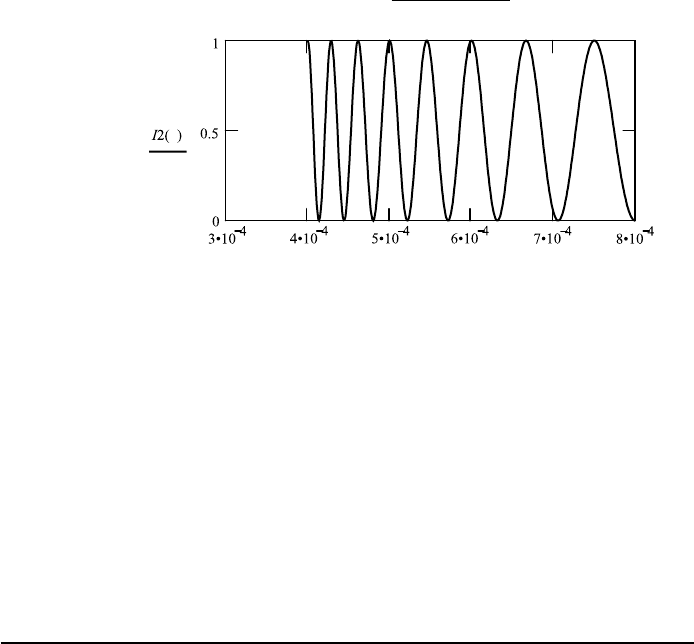
The ﬁrst graph in FileFig 2.12 shows the fringes depending on thickness D.

The second graph shows the fringes depending on wavelength λ.

FileFig 2.12 (I2MICHDLS)

Intensity of the Michelson interferometer depending on the displacement D of one

mirror for wavelength λ  .0005 mm, and for dependence on λ for D  .003.

I12MICHDLS

Michelson Interferometer

Beam splitter is assumed to be a plane parallel plate. Fringe pattern depending

on D for wavelength λ  .0005, and depending on wavelength λ for D  .003.

The angle θ  0. All lengths in mm.

1. Dependence on D.

θ : 0 λ;.0005

D : 0.027,.02701 ....0325

I 1(D): cos



2 ·π · D · cos(θ )



106 2. INTERFERENCE

2. Dependence on λ

λ : .0004,.000401 ....0008

D : .003

I 2(λ): cos



2 ·π · D · (θ )



Application 2.12.

1. Resolution depending on displacement D. Add to the graph of the intensity

depending on D a graph with a second wavelength λλ  λ+λ; for example,

λλ  0.00052. Observe that the separationof the fringes gets larger for larger

m. For the mth fringe we have the path differences mλλ and mλ. When this

difference is λ/2, we call the two fringes resolved and have mλλ−mλ  λ/2,

mλ  λ/2,orλ/λ  2m. Compare the formula λ/λ  2m with values

read from the graph for choice of λλ.

2. Add to the graph of the intensity depending on λ a second graph with different

D value. The graph shows the change in phase for one wavelength when D is

changed. Choose D

such that maxima change to minima and D

that mimima

change to the next maxima. Read from the graph the numerical values and

compare with the formula for constructive and destructive interference.

2.5.3.2 Michelson Interferometer, Nonnormal Incidence, Heidinger, and Fizeau

Fringes

If the light from the point source ﬁlls a cone with opening angle θ, the distance

− x

depends on the angle θ and a ring pattern will result in the plane of

the observation screen. For the mathematical treatment we fold one beam of the

Michelson interferometer over to the other beam as shown in Figure 2.15a. To

calculate the path difference of the two beams (1) and (2), we use Figure 2.15b

and calculate the path difference using Figure 2.15c. We have for the distances

[ab]  [bc]  D/ cos θ, and for the distance [ac]  [(2D/ cos θ)(sin θ )] 

2D tan θ . The optical path difference δ is then

δ  2[bc] −[ac] sin θ  2D/(cos θ ) −2D tan θ sin θ  2D cos θ. (2.62)