Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple
Подождите немного. Документ загружается.

2.7. RANDOM ARRANGEMENT OF SOURCE POINTS 127
The result for the intensity in the case where the array is not periodic is
I
R
A
2
N. (2.123)
We compare this result to Eq. (2.117), that is, for the periodic array. For maxima
we obtained
I
A
A
2
N
2
. (2.124)
This is an important result for the discussion of phenomena having their origin in
periodic and non periodic appearance. In our case of interference, one has for the
non periodic case an “incoherent” addition of the waves. The result is an average
distribution I ∝ N, and there is no interference pattern. In the periodic case, the
waves add coherently and an interference pattern is observed. The light appears
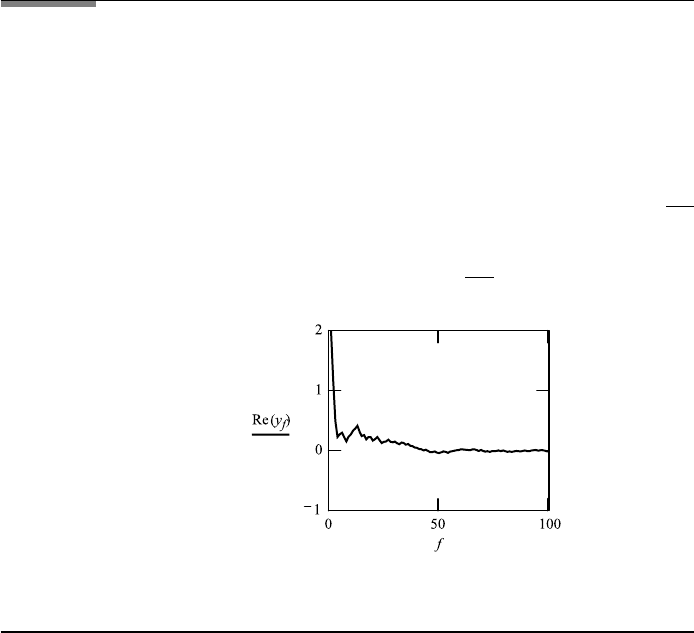
as maxima and minima. In FileFig 2.21 we show the incoherent addition of the
waves for the non periodic case. The sum of Eq. (2.122) is plotted depending
on the number N
f
of randomly positioned openings and approaches zero when
choosing large numbers of N
f
.
FileFig 2.21 (I21RANDS)
Incoherent addition of N phase factors.
I21RANDS
Addition of Exponential Functions with Random Angles
The real part of the sum of exp iθ is plotted.
f : 1 ...100 N
f
: fk: 1, 2,...1000 i :
√
−1
θ
k
: rnd(2 · π) y
f
:
1
N
f
·
N
f
k0
e
i·(θ
k
)
.
Application 2.21. Change f to a small value and then increase it and observe
the changes in the average.
128 2. INTERFERENCE
See also on CD
PI1. Cos-Waves depending on Space and Time (see p. 80).
PI2. Superposition of two cos-waves with fixed Optical path Difference (see
p. 82).
PI3. 3-D Graph of Maxima and Minima (see p. 84).
PI4. Average( see p. 85).
PI5. Fresnel’s Mirrors (see p. 93).
PI6. Young’s and Lloyd Experiment (see p. 93).
PI7. Plane parallel Plate in two Beam Interferometry with different Refractive
Indices (see p. 95).
PI9. Wedge shaped Film (see p. 99).
PI10. Newton’s Rings (see p. 101).
PI11. Ring pattern and Michelson interferometer (see p. 107).
PI12. Plane parallel plate (see p.108-111).
PI13. Interference of white light on a thin film (see p. 113).
PI14. Reflection and Transmission coefficients (p. 111–112).
PI15. Plane parallel plate, graphs depending on wavelength (see p. 113).
PI16. Dependence on angle of the Finesse (p. 117).
PI17. Plane parallel plate with mirror surface.
PI18. Fabry-Perot (see p. 115).
PI19. Interference with an array of source points (see p. 122).
PI20. Summation of random phase angles (see p. 125).

3
3
CHAPTER
Diffraction
3.1 INTRODUCTION
We know Huygens’Principle from introductory physics. It tells us that a “new”
wavefront of a traveling wave may be constructed at a later time by the envelope
of many wavelets generated at the “old” wavefront. One assumes that a primary
wave generates fictitious spherical waves at each point of the “old” wavefront.
The fictitious spherical wave is called Huygens’wavelet and the superposition of
all these wavelets results in the “new” wavefront. This is schematically shown in
Figure 3.1. The distance between the generating source points is infinitely small
and therefore, integration has to be applied for their superposition.
We discussed in Chapter 2 the superposition of light waves and the resulting
interference patterns. In the division process of the incident wave into parts, we
neglected the effect of diffraction. In this chapter we take into account interfer-
ence and diffraction of the wave incident on an aperture. Optical path differences,
FIGURE 3.1 Schematic of wavefront construction using Huygens’ Principle.
129

130 3. DIFFRACTION
FIGURE 3.2 Conditions for diffraction on a single slit: (a) d λ, no appreciable diffraction; (b)
d of the same order of magnitude of λ, diffraction is observed (fringes); (c) d λ, nonuniformly
illuminated observation screen, but no fringes.
generated between adjacent light waves, are finite for the superposition process
of interference and infinitely small for diffraction.
If we apply this division process to an open aperture, the incident wave gen-
erates new waves in the plane of the aperture, and these newly generated waves
have fixed phase relations with the incident wave and with one another. We as-
sume that all waves generated by the incident wave propagate only in the forward
direction, and not backward to the source of light. Let us consider the diffraction
on a slit (Figure 3.2). The observed pattern depends on the wavelength and the
size of the opening. A slit of a width of several orders of magnitude larger than
the wavelength of the incident light will give us almost the geometrical shadow
(Figure 3.2a). A slit of width of an order or two larger than the wavelength
will bend the light and fringes will occur; see Figure 3.2b. A slit smaller than the
wavelengthwill showan intensity pattern with no fringes and decreasing intensity

3.2. KIRCHHOFF–FRESNEL INTEGRAL 131
for larger angles; see Figure 3.2c. All openings will show small deformations of
the wavefront close to the edges of the slit (not shown in Figure 3.2).
The model we are using for the description of diffraction is called scalar wave
diffraction theory and uses the Kirchhoff–Fresnel integral. All the waves we
consider are solutions of the scalar wave equation, as used for the discussion of
the interference phenomena in Chapter 2. Here we use spherical waves of the
type Ae
ikr
/r, where A is the magnitude of the wave, r the distance from the
origin, and k 2π/λ. These spherical waves are solutions of the scalar wave
equation
∇
2
u + k
2
u 0. (3.1)
Written in spherical coordinates r, θ , and φ one has
∇
2
(1/r
2
){∂/∂r(r
2
∂/∂r)}+ (terms in θ and φ), (3.2)
where we have not explicitly given the terms in θ and φ because we only use
spherical symmetric solutions and they do not depend on the angular terms.
There is the question of why we should use a summation process based on
the idea of Huygen’s Principle to describe diffraction theory. Why not solve
Maxwell’s equations with the appropriate boundary conditions? The mathemat-
ical formulation of Huygens’ Principle was performed by Gustav Kirchhoff and
Augustin Jean Fresnel before Maxwell’s theory was developed. It turned out
that the use of the Kirchhoff–Fresnel integral for many applications is so much
easier than solving Maxwell’s equations and applying boundary conditions, that
one just continues to use the scalar wave diffraction theory. The wavelength is
assumed to be smaller than the aperture opening under consideration.
3.2 KIRCHHOFF–FRESNEL INTEGRAL
3.2.1 The Integral
We assume for the summation process of the Huygens’wavelets, that the primary
wave from the source S has amplitude A and travels distance R in the direction
of the aperture (Figure 3.3). We disregard the time factor for all waves consid-
ered in this chapter. We recall that in Chapter 2 the time factor disappeared when
calculating the intensity. At each point of the aperture a Huygens’wavelet is gen-
erated, [(1/ρ) exp(ikρ)], and travels only in the “forward” direction (Figure 3.3).
It has the amplitude of the incident wave, that is, {(A/R) exp(ikR)}.Wehavefor
a newly generated wavelet
[(A/R) exp(ikR)](1/ρ) exp(ikρ) exp(iα), (3.3)
where exp(iα) is a phase factor related to the generation process. However, it is
set to 1.
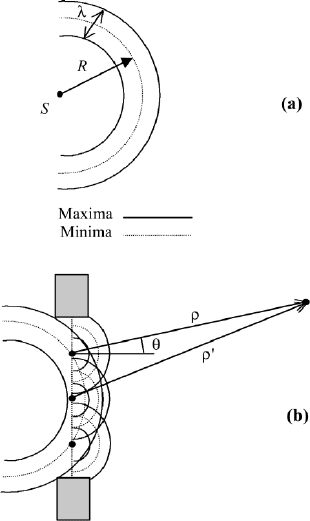
132 3. DIFFRACTION
FIGURE 3.3 (a) Maxima and minima of incident wave; (b) three newly generated Huygen’s
wavelets are shown at the aperture.
From experiments we know that there is an angular dependence of the in-
tensity in the direction of propagation. Therefore we multiply by cos θ , where
θ is the angle to the normal of the aperture, pointing into the forward direc-
tion. Integration over all points of the aperture results in the Kirchhoff–Fresnel
integral,
(A/R) exp(ikR)(1/ρ) exp(ikρ) cos θdσ, (3.4)
opening of aperture
where dσ is the surface element for integration over the opening of the aperture.
This integralmay be derived from the scalar wave equation and Green’s Theorem.
The derivation yields the factor cos θ and shows that the diffracted light is only
traveling in the forward direction. However, there are some problems with the
boundary conditions. A formulation using Green’s function avoids this problem,
but is not necessarily better. For more information, see Goodman, 1988, p. 42.
In the following two sections we apply Eq. (3.4) to a special symmetric ar-
rangement of source and observation points, both at large distances from the
aperture. We calculate the diffracted intensity only at one observation point on

3.2. KIRCHHOFF–FRESNEL INTEGRAL 133
FIGURE 3.4 Coordinates for the circular opening. The source point and the observation point
have the same distance from the aperture.
the axis of the system for the diffraction on a round aperture and a round stop.
These calculations are taken from Sommerfeld’s book on theoretical physics.
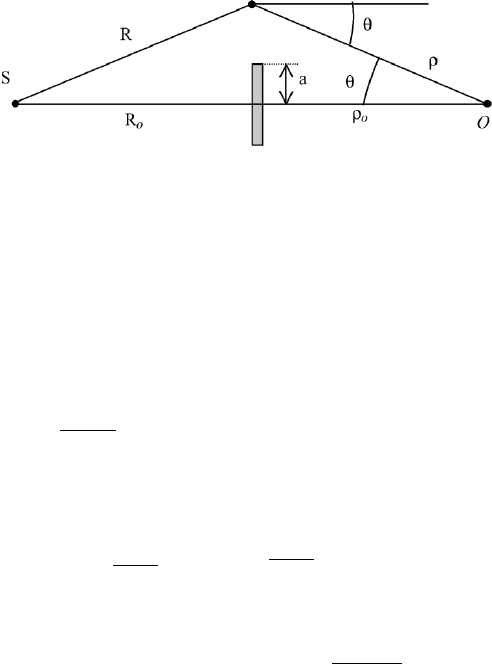
1
3.2.2 On Axis Observation for the Circular Opening
The diffraction on a round opening is important since most lenses, spherical
mirrors, and optical instruments have circular symmetry. We consider a round
aperture of radius a with equal distance to the aperture of the source point S and
the observationpoint O. In Figure 3.4 we showthe coordinates and have R
0
ρ
0
,
R ρ, cos θ ρ
0
/ρ, and for the surface element dσ 2πrdr. The amplitude
at the observation screen is then obtained by the integral over the opening
u A
{(1/Rρ) exp(ik(R + ρ))}{ρ
0
/ρ} 2πrdr. (3.5)
opening
The integration limits are from ρ
0
to
(a
2
+ ρ
2
0
). We get from r
2
+ ρ
2
0
ρ
2
that rdr ρdρ and have
u A2πρ
0
√
(a
2
+ρ
2
0
)
ρ
0
(1/ρ
2
) exp(ik2ρ)dρ. (3.6)
Integration by parts with u 1/ρ
2
, dv e
ik2ρ
, and v (1/2ik)e
ik2ρ
results in
(1/ρ
2
)(1/2ik)e
ik2ρ
√
(a
2
+ρ
2
0
)
ρ
0
+(1/ik)
√
(a
2
+ρ
2
0
)
ρ
0
(1/ρ
3
)e
ik2ρ
dρ.
Since ρ is large, we retain only the first term with the power of 1/ρ
2
and have
u (2πAρ
0
/2ik)
e
i2k
√
a
2
+ρ
2
0
/(a
2
+ ρ
2
0
) − (exp{i2kρ
0
})/ρ
2
0
. (3.7)
1
Vorlesungen uber theoretische Physik, Band IV, by A. Sommerfeld. Dieterich’sche Verlagsbuchhandlung,
Wiesbaden, 1950.
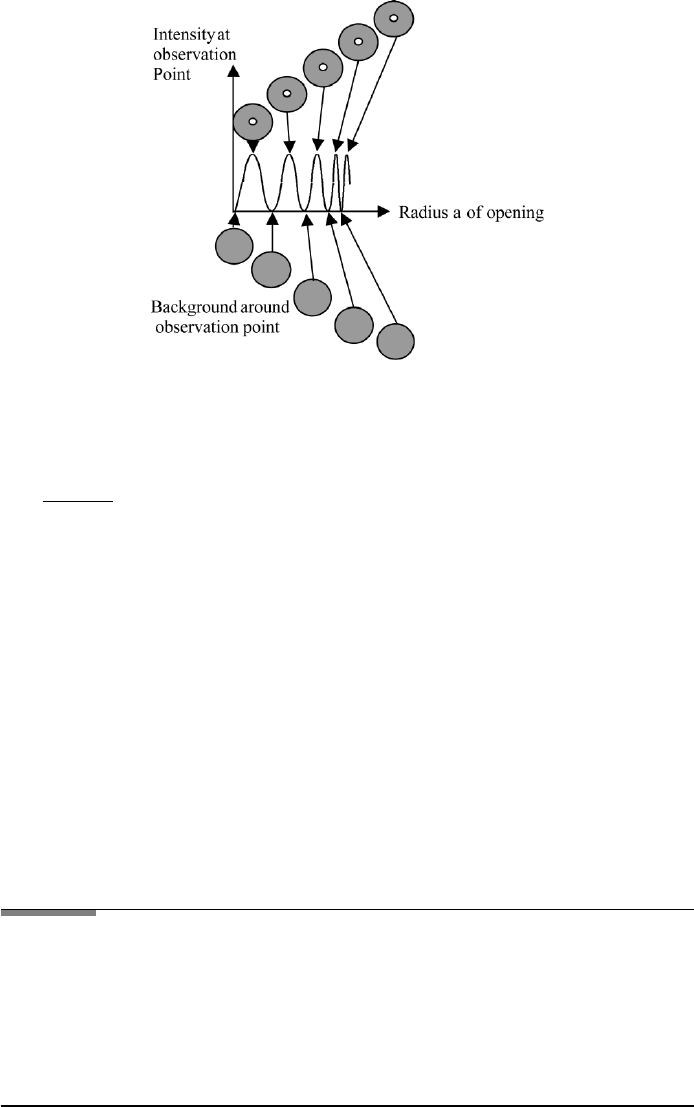
134 3. DIFFRACTION
FIGURE 3.5 Diffraction pattern for a circular aperture at the observation point. The intensity has
a maximum for certain values of the radius a, shown as a white spot on the gray background. For
other values of a the intensity is zero; only the gray background is shown.
Further simplification is obtained by assuming ρ
0
a,
a
2
+ ρ
2
0
≈ ρ
0
(1 + a
2
/2ρ
2
0
), (3.8)
and obtaining for the amplitude
u (2πAρ
0
/2ik)(exp{i2kρ
0
})(1/ρ
2
0
)[exp{ik(a
2
/ρ
0
)}−1]. (3.9)
The intensity uu
∗
is obtained after normalization as
I I
0
λ
2
sin
2
(ka
2
/2ρ
0
). (3.10)
In Figure 3.5 we show maxima and minima for different radii a of the circular
opening, at the center. Our calculation refers to the center spot only and the radius
of the corresponding maxima or minima may be read from the graph in FileFig
3.1.
FileFig 3.1 (D1CIRS)
In FileFig 3.1 we show a graph of the intensity at the center. We use λ
0.0005 mm, ρ
0
4000 mm, and radius a of 0.1 to 5 mm. With increasing
diameter of the aperture, that is, with increasing a, we have at the center a
change from maxima to minima to maxima and so on.
D1CIR is only on the CD.
3.2. KIRCHHOFF–FRESNEL INTEGRAL 135
FIGURE 3.6 Coordinates for the circular stop. The source point and the observation point have
the same distance from the aperture.
3.2.3 On Axis Observation for Circular Stop
In optics, it is often of interest to study complementary screens or arrays. We
apply the Kirchhoff–Fresnel integral, Eq. (3.4), to a circular stop, as shown in
Figure 3.4. Similar to the “opening,” we must now evaluate
u A2πρ
0
∞
√
(a
2
+ρ
2
)
(1/ρ
2
) exp(ik2ρ)dρ. (3.11)
Integration by parts yields
(1/ρ
2
)(1/2ik)e
ik2ρ
∞
√
a
2
+ρ
2
0
+(1/ik)
∞
√
a
2
+ρ
2
0
(1/ρ
3
)e
ik2ρ
dρ. (3.12)
Neglecting the last integral we get
u (2πAρ
0
/2ik)[−{1/(a
2
+ ρ
2
0
)}]{exp(i2k
a
2
+ ρ
2
0
)}. (3.13)
Multiplication of u in Eq. (3.13) by u
∗
yields the intensity, and taking for the
normalization I
0
A
2
ρ
2
0
/(a
2
+ ρ
2
0
), we have
I I
0
λ
2
/4. (3.14)
The intensity of Eq. (3.14) depends only on the wavelength, not on the diameter
of the aperture or the distance from it. We have the result that at any point in the
shadow of an aperture stop, we will observe a bright spot.
There is the story that Fresnel presented his wave theory of light to the French
Academy of Sciences. The famous Poisson questioned the validity and argued
that there should be a light spot in the shadow of an illuminated sphere, for
example, a steel ball. Another scientist of the Academy, Arago, made the exper-
iment, observed the spot and presented his finding to the Academy in support of
Fresnel’s theory, but the spot remains the “Poisson spot.” A photograph of the
Poisson spot and an experimental setup for observation are shown in Figure 3.7.
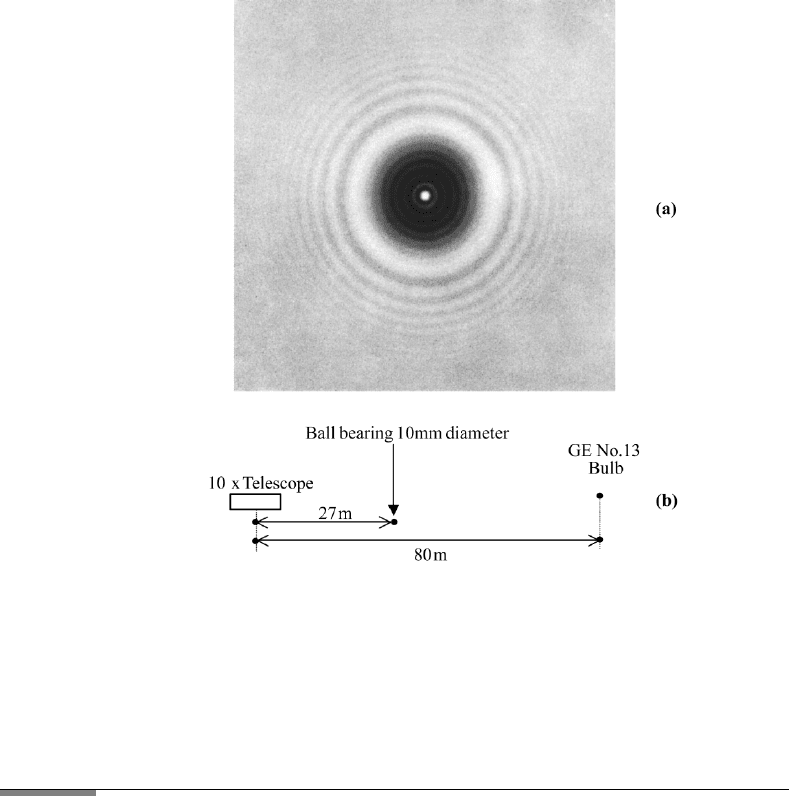
136 3. DIFFRACTION
FIGURE 3.7 (a) Photograph of the diffraction pattern produced by a round stop. The Poisson
spot appears in the middle (from Cagnet, Francon, Thrierr, Atlas of Optical Phenomena, Springer-
Verlag, Heidelberg, 1962); (b) parameters for the observation of the Poisson spot (after R. Pohl.
Einf¨uhrung in die Optic, R.W. Pohl, Springer-Verlag, Heidelberg, 1948).
3.3 FRESNEL DIFFRACTION, FAR FIELD
APPROXIMATION, AND FRAUNHOFER
OBSERVATION
In the first two applications of the Kirchhoff–Fresnel integral, we have assumed
that the source of light and the observation point are at large distances from
the aperture. How large was not specified. When assuming that the distance is
“infinitely large,” so large that we essentially have plane waves incident on the
aperture, we are at the approximation used in Chapter 2. When observing at
a screen similarly far away from the aperture, the waves arriving there are also
considered plane waves and are also parallel for their superposition. This is called
far field approximation.When we use a lens and observe the diffraction pattern in
the focal plane, we have Fraunhofer diffraction. The mathematical presentation
of far field approximation and Fraunhofer diffraction is the same. In contrast,
when the distance from the aperture to the observation screen is large but finite,
