Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple

Подождите немного. Документ загружается.

3.4. FAR FIELD AND FRAUNHOFER DIFFRACTION

157

2. Use FileFig 3.9 for the amplitude grating with d  0.0018 mm, λ  0.0005

mm, a  0.0036 mm, and θ −1.401 to 1.4.

a. How is the width of the main maxima dependent on the diffraction angle

θ?

b. What happens to the main maxima if we change d to 0.0009?

c. For blue light use λ  0.0004 mm and for red light λ  0.0007 mm. Plot

for both the interference and diffraction factor on one graph and compare

the two intensity patterns for different values of N .

d. Use close values of the two wavelengths, (e.g., 0.0005 and 0.00055) and

determine when two peaks of different wavelengths and at different orders

may be resolved depending on choices of N . (For changes in the angle,

we have that 1 rad is about 5 to 6 degrees.)

3. From the interference factor ﬁnd the numerical values of sin θ for which the

interference factor is equal to N

(or 1 in the normalized case). Express the

numerical factor in terms of a, m, and λ; this is the grating equation.

FileFig 3.10 (D10FAGRDSLS)

Graph of the intensity P (Y ) of a double slit for d  0.02, λ  0.0005, a  0.2,

X  4000, N  2, and Y −800, −799.9 to 800. A photograph is shown in

Figure 3.18.

D10FAGRDSLS is only on the CD.

Application 3.10.

1. When d is changed from d  a/2 to d  a, what happens to the diffraction

factor D(Y ) and how is the intensity P (Y )  D(Y )I (Y ) affected, where I (Y )

is the interference factor?

2. From Figure 3.16 one can obtain (a sin θ)  mλ with an elementary deriva-

tion. This is the grating equation. This equation may also be obtained from

the formula of the intensity for the main maxima. Using this formula make a

FIGURE 3.18 Diffraction pattern of a double slit where the separation a of the slits is much larger

than the width d. The central part of the diffraction pattern shows an interference pattern similar

to that observed in Young’s experiment (from M. Cagnet, M. Francon, and J. C. Thrieer, Atlas of

Optical Phenomena, Springer-Verlag, Heidelberg, 1962).

158 3. DIFFRACTION

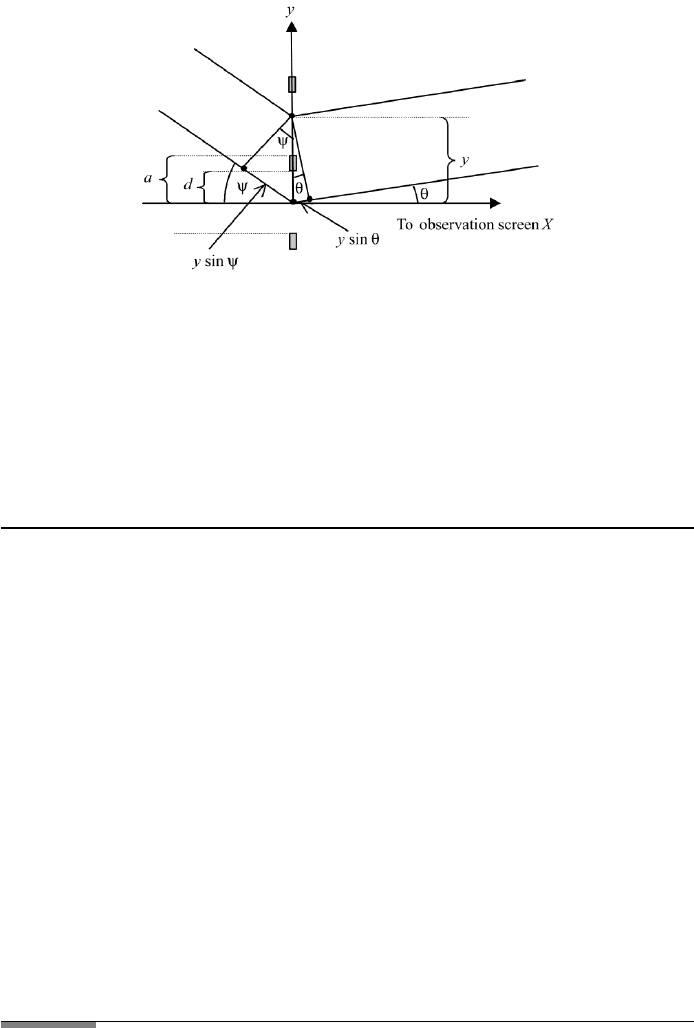
FIGURE 3.19 Coordinates for the amplitude grating. The incident light has angle ψ with the X

direction.

list of the maxima depending on Y , for d  a/10, and compare with P (Y ) of

the graph.

3. Missing order: Use 4d  a and start counting the maxima of P (Y ) from the

center at 0. The fourth maximum of I (Y ) is suppressed by the factor D(Y ).

Use other ratios of a/d.

4. Continue (3) on missing order. Change the wavelength to twice its value and

to 1/2 and see what happens to the pattern.

3.4.5.2 Amplitude Grating with Incidence Light at an Angle

An experimental setup may require that the incident light enter the grating not

in the direction of the normal but under an angle ψ with respect to the grating

surface (Figure 3.19). The only difference now is that the optical path difference

(i.e., a(sin θ) of the two parallel beams; see Eq. (3.54) is enlarged by the term

a(sin θ). One obtains for the intensity

I (θ ) {[sin(πd(sin θ +sin ψ)/λ)]/[πd(sin θ + sin ψ)/λ)]}

·{sin[πNa(sin θ +sin ψ)/λ]/N sin[πa(sin θ + sin ψ)/λ]}

. (3.61)

The interference diffraction pattern is similar to the pattern of the amplitude grat-

ing used at normal incidence. The difference is that the main maximum is not at

θ  0. The normalized interference factor is equal to 1 for the main maximum,

that is, for (sin θ +sin ψ)  0, or at sin θ −sinψ. The zeroth order is shifted

from θ  0toθ −ψ. This is shown in the graph of FileFig 3.11.

FileFig 3.11 (D11FAGRANGS)

A graph is shown of the diffraction pattern of an amplitude grating with the

incident light under an angle ψ to the normal.

3.4. FAR FIELD AND FRAUNHOFER DIFFRACTION

159

D11FAGRANG is only on the CD.

Application 3.11. Find the numerical values of (sin θ + sinψ) for which the

normalized interference factor is equal to N

. Express the numerical factor in

terms of a, m, and λ and compare with the grating equation.

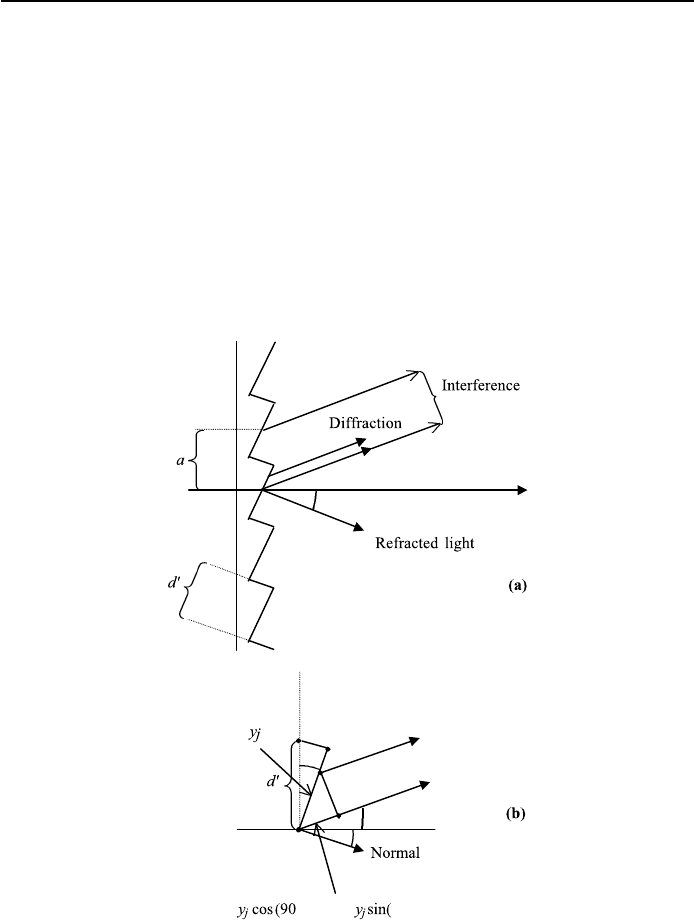
3.4.5.3 Echelette Grating (Phase Grating)

A transmission grating with periodic differences in thickness is called a phase

grating. When the grating has steps with angle ε, as shown in Figure 3.20, it

is called an echelette grating. It may be produced from materials of refractive

index n or with a metal surface such as a reﬂection grating. To calculate the

interference diffraction pattern of the echelette grating, we have to determine

the optical path difference between equivalent wavelets from neighboring steps

and integrate over all the steps. The result is an interference factor, depending

on the periodicity constant a of the steps and a diffraction factor, depending on

−θ

− θ − ε) = θ + ε)

−ε

FIGURE 3.20 Coordinates for an echelette grating: (a) refracted and diffracted light and interfer-

ence; (b) coordinates for the diffraction on one facet. Integration of the diffraction factor over the

facet uses the optical path difference y

sin(θ + ε). The maximum is at θ −ε. We set d



 d.

160 3. DIFFRACTION

the shape of the step. To make the calculation of the diffraction factor easy, we

assume that the periodicity constant is equal to the width of the steps d and we

choose the angle of incidence such that the transmitted light is refracted in a

direction perpendicular to the plane of the step (Figure 3.20a). The angle ε is

then the angle between the normal of the facet and the normal of the plane of

periodicity. The intensity is again given as the product of the interference and

diffraction factor. The interference factor is the same as the one obtained for the

amplitude grating, but the diffraction factor is calculated with the optical path

difference y

sin(θ + ε); see Figure 3.20. The intensity is then

I (θ ) {[sin(πd sin{θ +ε}/λ)]/[πd sin{θ + ε}/λ]}

(3.62)

·{[sin(πNa sin θ/λ)]/N sin(πasin θ)/λ]}

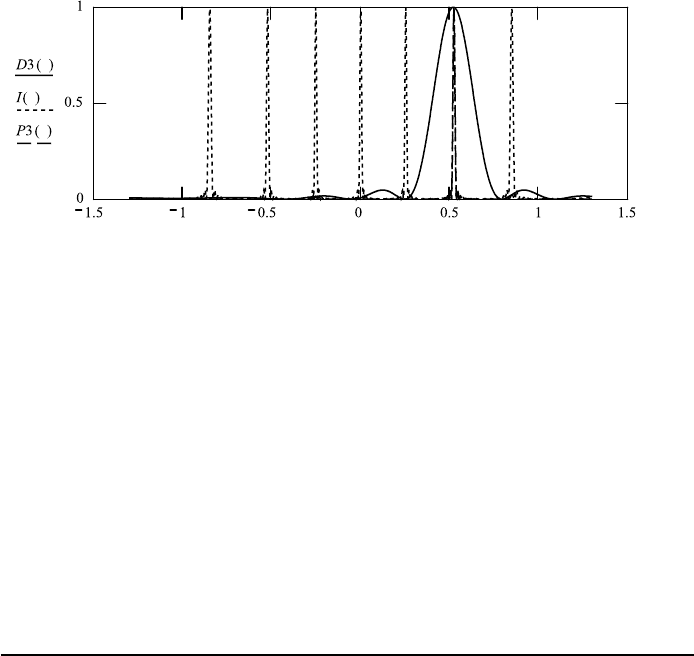
The three graphs in FileFig 3.12 demonstrate the dependence on the step angle

ε. When ε −.25 we see that the maximum of the diffraction factor is lined

up with the ﬁrst-order maximum of the interference factor. The zeroth order of

the interference factor is at the ﬁrst minimum of the diffraction factor and is

suppressed. For the particular wavelength the grating is said to be blazed. For

slightly different wavelengths, the ﬁrst order would be displaced within the enve-

lope of the diffraction factor. Considering a source emitting many wavelengths,

the ﬁrst order of a range of wavelengths is distributed over the range determined

by the diffraction factor.

When changing the step angle ε, one has for ε  .25 that the zeroth order of

the diffraction factor is shifted to the −1 order of the interference factor (see the

second graph of FileFig 3.12). For ε −.52, the zeroth order of the diffraction

factor is at the +2 order of the interference factor (third graph of FileFig 3.12).

For other values of (between these values, one ﬁnds that the maxima of the

interference factor are not lined up with the maxima of the diffraction factor.

FileFig 3.12 (D12FAELGRS)

Graphs of the intensity of diffraction on an echelette grating. Three graphs are

shown for three values of ε. There is only one interference factor and three

diffraction factors. We see that the diffraction factor is lined up with the ﬁrst

maximum of the interference factor for ε −0.25. The zero order of the inter-

ference factor is at the ﬁrst minimum of the diffraction factor and is suppressed.

If one applies a source emitting many wavelengths, the ﬁrst-order of a narrow

band of different wavelengths is “ﬁlling” the area of the diffraction factor. For the

wavelength for which both maxima coincide, the grating is said to be “blazed.”

When choosing ε  0.25 the zeroth order of the diffraction factor is shifted to

the −1 order of the interference factor. For ε −0.52 we have the zeroth order

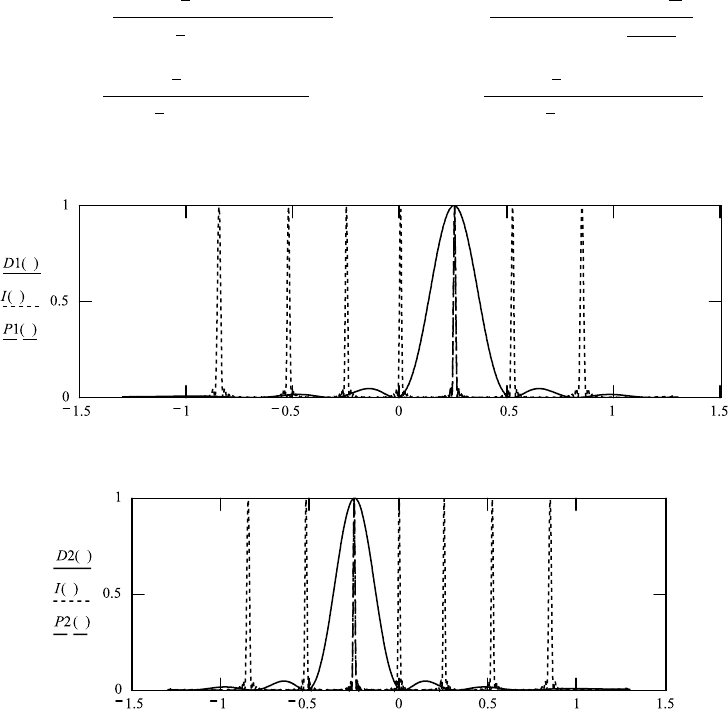
3.4. FAR FIELD AND FRAUNHOFER DIFFRACTION 161

of the diffraction factor at the +2 order of the interference factor. We may choose

other values of ε and ﬁnd a misalignment.

D12FAELGRS

Diffraction on an Echelette Grating

The graphs for the three different values of . D(θ ) is the diffraction factor,

I (θ ) the interference factor, and P (θ) the product. The angle in radians of the

echelette is . Diffraction angle θ in radians, wavelength λ, width of openings

d, and separation of openings a in mm. N is the number of lines. All parameters

are deﬁned globally above the graph.

θ :−.301, −1.299 ...1.3

D1(θ):



sin



π ·

· (sin(θ + 1))



π ·

· sin(θ + 1)





I (θ ):



sin



π · a · (sin(θ )) ·

N · sin



π · a ·

(sin(θ ))



D2(θ):



sin



π ·

· sin(θ + 2)





π ·

· sin(θ + 2))



D3(θ):



sin



π ·

· (sin(θ + 3))



π ·

· sin(θ + 3)





P 1(θ): D1(θ) · I (θ) P 2(θ): D2(θ) · I (θ ) P 3(θ): D3(θ) · I (θ )

1 ≡−0.25 d ≡ 37 λ ≡ 10 a ≡ 40 N ≡ 20.

2 ≡ 0.25.

162 3. DIFFRACTION

3 ≡ 0.52.

Application 3.12. Use FileFig 3.12 with d  0.04, a  0.04, λ  0.01, and

N  20.

1. Start from ε  0 and use for ε positive numbers until the negative ﬁrst-order

of I(θ) is at the peak of D(θ). Make another graph using a negative value for

ε until the positive ﬁrst-order of I (θ ) is at the peak of D(θ).

2. Make three graphs with nine plots, starting with P 1(θ ), D1(θ), and I 1(θ ) for

λ1  0.015, then P 2(θ), D2(θ), and I 2(θ ) for λ2  0.01, and

P 3(θ), D3(θ),

and λ3(θ ) for λ3  0.007. Find a value of ε such that the interference peak

of the positive ﬁrst order of λ2 is at the maximum of the diffraction factor. The

grating is now “blazed” for the wavelength λ2  0.01. Make an extra plot

only of P 1(θ ) to P 3(θ) and see that for the wavelengths λ1 and λ3 more than

one peak appears. These wavelengths do not have maximum intensity and

two orders would be observed. The echelette grating would be less efﬁcient.

3.4.6 Resolution

Gratings are used in spectrometers to obtain the spectrum of the incident light. Let

us consider incident light containing a spectrum of just two different wavelengths

and λ

. As an example let us consider the sodium D lines at 5890 and 5896

◦

in the yellow part of the visible spectrum, emitted when the Sodium atom

is at a high temperature. One may observe these lines when salt falls into a gas

ﬂame and one sees yellow light. The wavelength difference of the two lines is

just 6

◦

and we now discuss the question of what has to be required of a grating to

observe the two separated lines. We consider two lines of wavelength difference

λ  λ

− λ

. The diffraction angles in the ﬁrst order will have maxima at

sin θ

 λ

/a and sin θ

 λ

/a (Figure 3.21a). Assuming λ

<λ

we have

to determine how large λ  λ

− λ

must be in order to recognize the two

spectral lines separately. If λ is large enough, we can recognize these two lines

(Figure 3.21b on the left) and if λ is too small, we would have just one peak

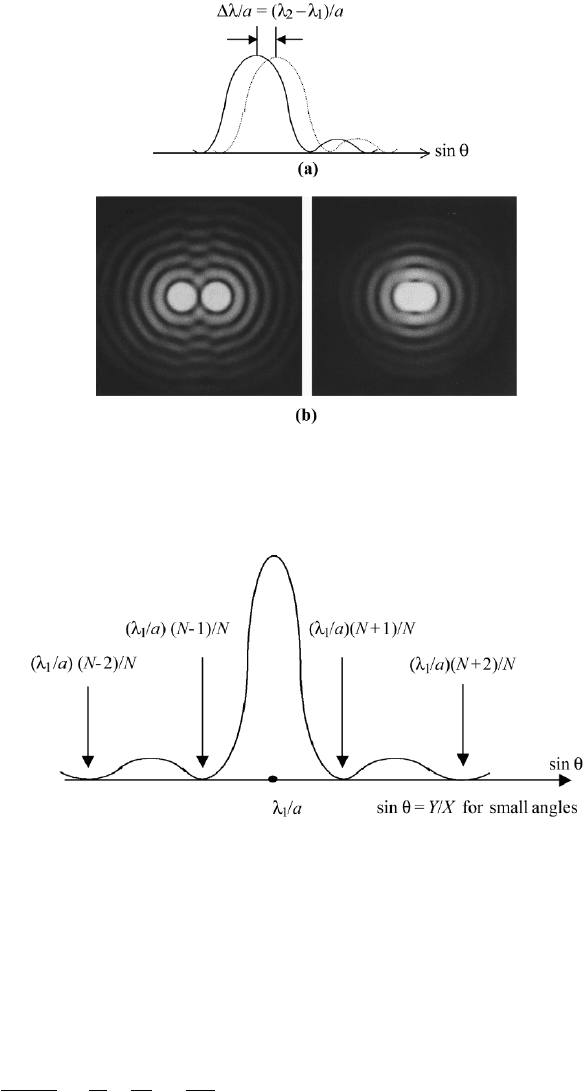
3.4. FAR FIELD AND FRAUNHOFER DIFFRACTION 163

FIGURE 3.21 (a) Closely positioned main maxima of the diffraction patterns produced by the

wavelengths λ

and λ

with λ  λ

− λ

; (b) (left) images of two point sources sufﬁciently

separated; (right) image of two point sources at the limit of resolution. (From M. Cagnet, M.

Francon, and J.C. Thrieer, Atlas of Optical Phenomena, Springer-Verlag, Heidelberg, 1962.)

FIGURE 3.22 Main maximum and side maxima of the diffraction pattern obtained with a grating

having N lines and using the wavelength λ

(Figure 3.21b on the right). To get a quantitative value for the case where the two

lines are just separated, we use the Rayleigh criterion. Which states that the two

maxima of a diffraction pattern are considered separated when the maximum of

one is at the position of the minimum of the other.

From Figure 3.22 we have for the distance from maximum to minimum of

the diffraction pattern of a grating for any order



N + 1

−





λ

(3.63)

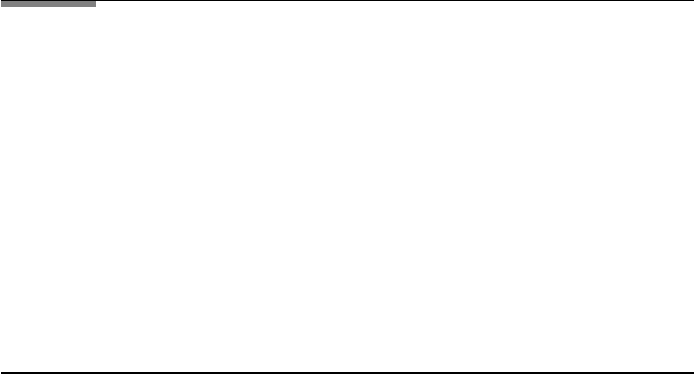
164 3. DIFFRACTION

and obtain

λ  λ

/N. (3.64)

Calling λ

just λ and considering the mth diffraction order, we have

λ/λ  mN. (3.65)

Since λν  velocity of the light in the medium, where ν is the frequency, one

also has

ν/ν  mN. (3.66)

The ratio λ/λ or ν/ν is called the resolving powers of the grating.

The graph in FileFig 3.13 shows two diffracted waves of wavelength λ

and

on a grating. The separation of their maxima depends on N and one may

change N to ﬁnd the separation in agreement with the Rayleigh criterion. Also

seen is the dependence of the resolution on the diffraction order. The ﬁrst graph

in FileFig 3.14 shows the diffraction pattern of two round openings of radius a.

One is at zero and the other at distance b. One can determine b using the Rayleigh

criterion. The second graph shows the two spectral lines in three dimensions.

For our example of the sodium D lines we have from Eq. (3.66) about 1000

for mN. In other words, in ﬁrst order we need 1000 lines of the grating. If the

grating has a periodicity constant of about 1 micron, the width of the grating

would be one millimeter. If one could use a larger grating of 10 cm then the

number of lines would be 100,000 and in ﬁrst order, for a wavelength of 5000

λ would be 0.02

FileFig 3.13 (D13FAGRRES)

Graph of the diffraction on an amplitude grating for two wavelengths λ



0.0005, λ

 0.0006, openings d  0.0001, periodicity constant a  0.002,

and number of lines N  6.

D13FAGRRES is only on the CD.

Application 3.13.

1. Make three choices of λ

and determine the N value so that the maximum of

is on the minimum of λ

2. Choose λ

and λ

and determine the N value necessary to resolve the two

maxima.

3. Consider higher orders m. Choose a pair of lines so close together that they

are not resolved in ﬁrst-order. Determine the order for resolution.

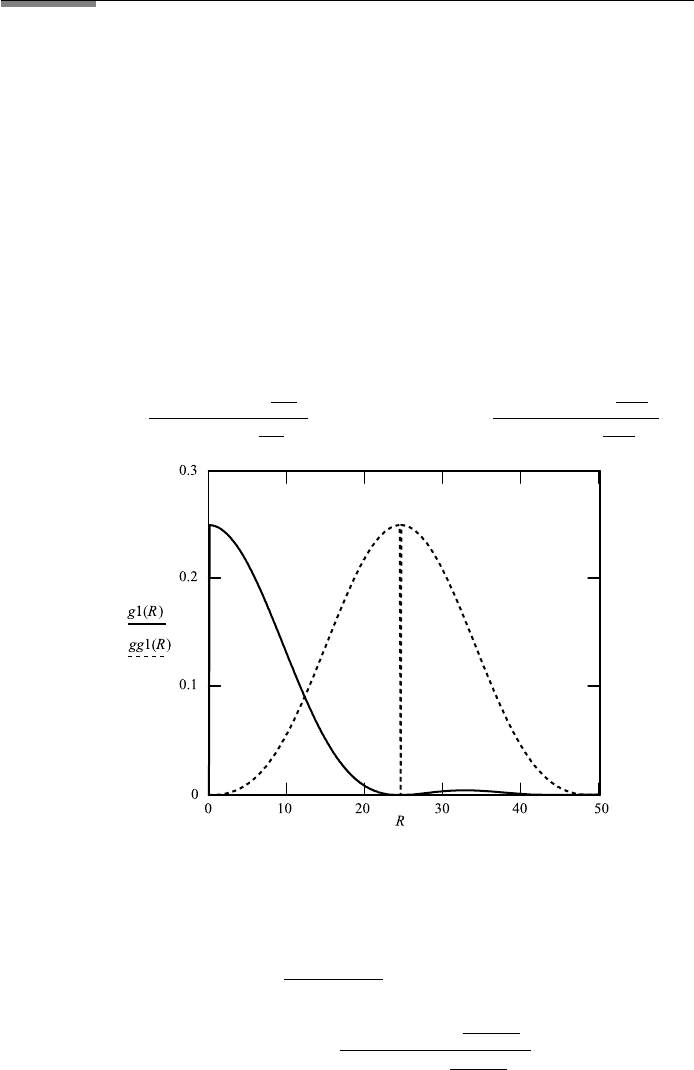
3.4. FAR FIELD AND FRAUNHOFER DIFFRACTION 165

FileFig 3.14 (D14FARES3DS)

Determination of Rayleigh distance and graph of the 3-D-diffraction pattern of

two round apertures of radius a and distance b.

D14FARES3DS

Determination of the Wavelength difference for Two Peaks, Resolved According to the

Rayleigh Criterion

We call the distance between the maxima b, radius of apertures a, distance

between the apertures d, coordinate on the observation screen R, wavelength λ,

and distance from aperture to screen X.

1. Determination of Rayleigh distance

a ≡ .05 X ≡ 4000 R : 0,.1 ...50

g1(R):



J 1



2 ·π · a ·

X·λ





2 ·π · a ·

X·λ





gg1(R):



J 1



2 ·π · a ·

R−b

X·λ





2 ·π · a ·

R−b

X·λ





Distance b is assumed to be b ≡ 24.5.

2. 3-D Graph of pattern of two round apertures at distance b

i : 0 ...N j : 0 ...N

: (−40) + 2.0001 · iy

: (−40) + 2.0001 · jλ≡ .0005

RR(x,y):



(x)

+ (y)

N ≡ 60 X : 4000

g2(x, y):



J 1



2 ·π · a ·

RR(x,y)

X·λ





2 ·π · a ·

RR(x,y)

X·λ





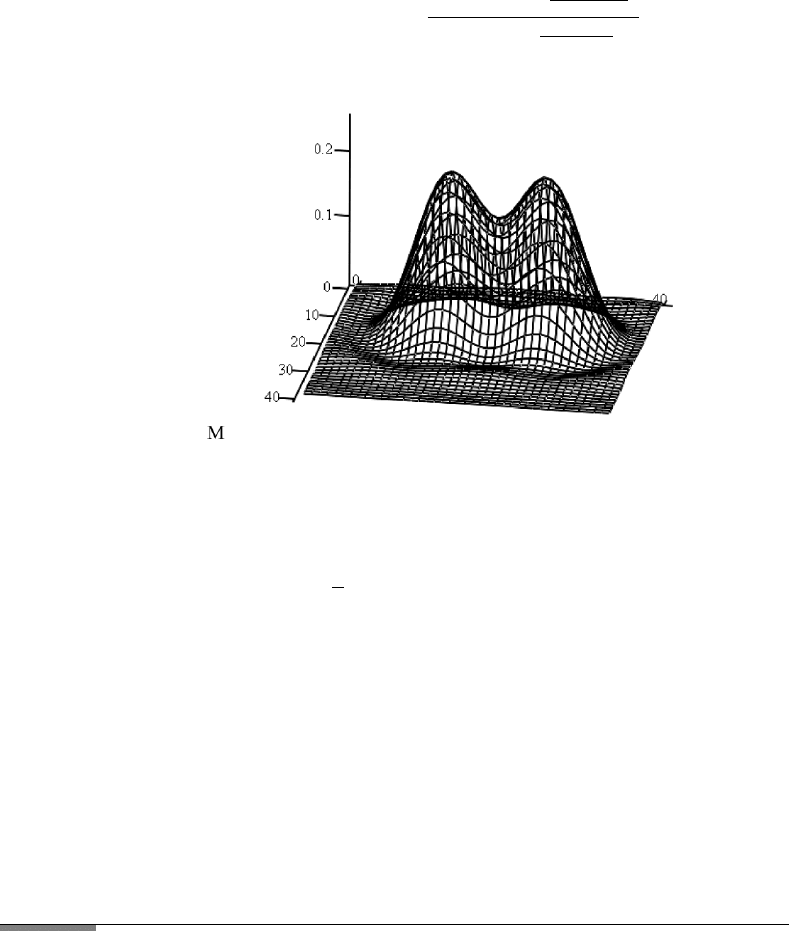
166 3. DIFFRACTION

gg2(x,y):



J 1



2 ·π · a ·

RR(x,y−b)

X·λ





2 ·π · a ·

RR(x,y−b

X·λ





i,j

: g2(x

) + gg2(x

3. Calculation of wavelength difference corresponding to b

The diffraction angle is calculated from b/X  θ. The grating is made of

round apertures of diameter a and spaced at distance d. From the grating

formula we have for the wavelength difference λ  dθ or λ  (d/X)b.

For d : .1, λ : d ·

, λ  6.125 ×10

−4

Application 3.14.

1. Convert to a surface plot and make b such that the maximum of one of the

peaks is on the minimum of the other. Then go back to the contour plot.

2. We have used the same wavelength for both peaks. After determining the

wavelength resolution, introduce the corresponding wavelengths into the two

expressions of the Bessel function and estimate the change.

3. Assume that the angle difference for resolution is given for order m and ﬁnd

the wavelength difference.

3.5 BABINET’S THEOREM

Babinet’s Theorem tells us that two complementary screens will give us the

same diffraction pattern at the observation screen. Complementary screens are

two screens, one of which is transparent at areas where the other is opaque

(Figure 3.23). If the two complementary screens are placed together in the same

plane, no aperture will exist.