Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple

Подождите немного. Документ загружается.

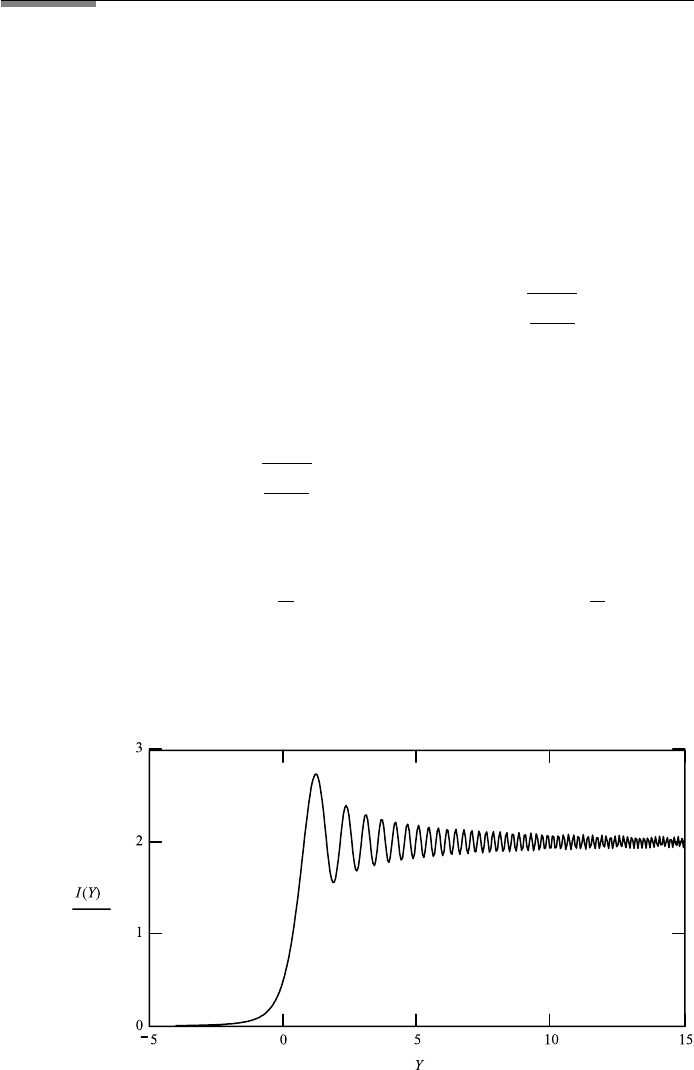
3.7. FRESNEL DIFFRACTION 177

FileFig 3.20 (D20FEEDGES)

The intensity I (Y ) for the diffraction on an edge is shown for the range from

Y −5 mm to Y +15 mm. To show that this is one side of a large slit, the

diffraction pattern of a large slit is shown as II(Y ).

D20FEEDGES

Fresnel’s Integrals for Calculation of Diffraction on an Edge

All units are in mm, global deﬁnition of the parameters.

Y :−4, −3.95 ...15 TOL ≡ .001

λ · X

 1

We treat the diffraction at an edge as diffraction on a large slit. One side is set

at d  0, the other at d −∞. This translates into

For p(Y ) −inﬁnte; we have Cp(Y )  Sp(Y ) −.5

q(Y ): (Y ) ·

λ · X

We take q(Y ) equal Y , square root is for scaling q(Y ): Y .

Cq(Y ):



q(Y )

cos



· η



dη Sq(Y ):



q(Y )

sin



· η



dη

I (Y ): (Cq(Y ) − (−.5))

+ (Sq(Y ) − (−.5))

X ≡ 4000

λ ≡ 5 ·10

−4

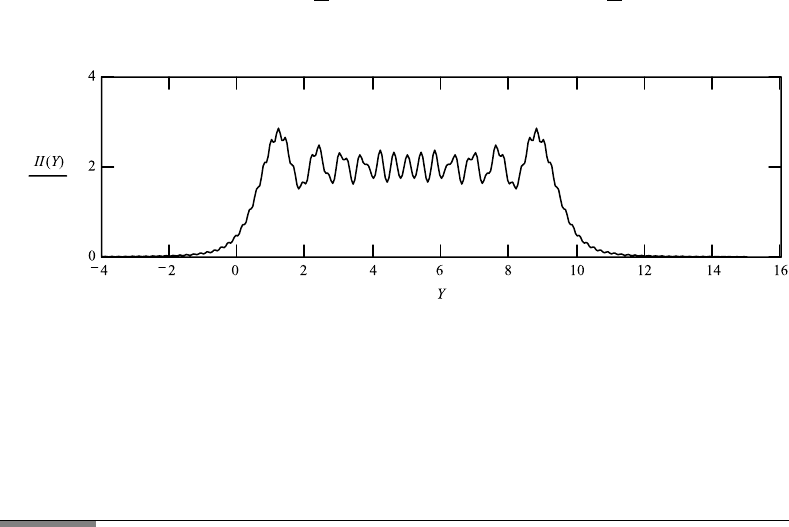
178 3. DIFFRACTION

To see that we actually derived this from a large slit, we treat a large slit with

positions at 0 and 10.

p(Y ):(Y − (10))

Cp(Y ):



p(Y )

cos



· η



dη Sp(Y ):



p(Y )

sin



· η



dη

II(Y ): (Cq(Y ) − Cp(Y ))

+ (Sq(Y ) − Sp(Y ))

Application 3.20. Vary the width of the slit by choosing values other than 10 in

P (Y )  Y − 10 and compare the diffraction pattern of the slit with the pattern

of the edge.

APPENDIX 3.1

A3.1.1 Step Grating

A grating with a rectangular reﬂecting surface is called a step grating. The grating

has the periodicity constant a, and the reﬂecting surfaces of length a/2 are

positioned in two planes. Such a grating may be produced by using two sets

of interpenetrating gratings, shown schematically in Figure A3.29. The distance

H between planes I and II may be varied, and the corresponding interference

diffraction pattern, depending on the height of H, is called an interferogram. As-

suming that the incident light contains many wavelengths, the application of a

Fourier transformation to the interferogram results in a spectrum.

We discuss here the step grating as shown in Figure A3.29b for a ﬁxed step

height H. The incident light is reﬂected at planes I and II and travels in direction

θ. At a faraway screen, one observes an interference diffraction pattern. We

calculate the diffraction pattern on the array of N steps, having width d, step

height H, and periodicity constant a.

Each of the two interpenetrating gratings produces the pattern of an amplitude

grating and, in addition, we have the interference of the light from planes I

3.7. FRESNEL DIFFRACTION 179

FIGURE A3.29 (a) Schematic of a step grating; (b) coordinates for the calculation of the diffraction

on a step grating. Only the emerging diffracted light is shown for the calculation of the path

difference. The two gratings in planes I and II interfere with each other in the X direction.

and II in the direction of the observation screen. The optical path difference

is δ  d sin θ + H and in order to get the intensity of the interference (see

Chapter 2, Eq. (2.8)), we have to insert this path difference δ into [cos(πδ/λ)]

The intensity P  uu

∗

of the diffraction and interference of each grating and

the interference of the two gratings with each other is then the product of the

diffraction factor

D(θ) {[sin(πd sin θ/λ)]/[(πd sin θ/λ)]}

, (A3.1)

the interference factor

I (θ ) {[sin(πNasin θ/λ)]/[N sin(πasin θ/λ)]}

, (A3.2)

and the step factor

ST (θ)  [cos{(π/λ)(d sin θ + H )}]

. (A3.3)

180 3. DIFFRACTION

The diffracted intensity is

P (θ) {[sin(πd sin θ/λ)]/[(d sin θ/λ)]}

{(sin πNasin θ/λ)/N sin(πasin θ/λ)}

· [cos{(π/λ)(d sin θ +h)}]

. (A3.4)

The diffraction pattern depends not only on d and a, but also on H. The graph of

FileFig A3.21 shows P (θ ) for several values of H and also the diffraction factor

D(θ). The diffraction factor supplies the envelope and the interference factor

supplies the lines. The zeroth order is at the center and the ﬁrst order is within

the envelope. Since we necessarily have 1:2 for the ratio d/a, the second order

is suppressed by the zeros of the diffraction factor. Variation of H will redis-

tribute the intensity between the zeroth and ﬁrst order. This may be understood

from energy conservation. We assume that the third and higher orders may be

neglected. Then for H  0, the incident light is reﬂected into the zeroth order,

that is, in the direction of reﬂection on the mirror surface. When H  λ/4, no

light can travel in the direction of the zeroth order. In other words, no light may

be reﬂected on the surface of the grating facets and all light travels into the ﬁrst

order. For H  λ/2 we have again reﬂection on the grating facets.

For H being a multiple of the wavelength, all light is diffracted into the zeroth

order and for H being a multiple of half a wavelength, all light is diffracted into

the ﬁrst order. The graph in FileFig A3.21 shows the intensity pattern P (θ) for

two different wavelengths. One observes only one peak for the zeroth order, but

two peaks for the ﬁrst order. The zeroth order changes its intensity depending

on H . Recording the intensity depending on H will reveal the interferogram.

FileFig A3.21 (DA1FAGSTEP1S)

There are four intensity patterns P 1 to P 4, each for a different value of H .

The values of H are presented as H  nλ. When n is an integer, we have all

light in the zeroth order. For noninteger values of n, we subtract from λ all full

wavelengths and look at the remaining fraction n



. For example, if n  10.5,

we look at n



 0.5. The optical path difference is now half a wavelength and

all the light is diffracted in the ﬁrst orders. For values such as 0.125, 0.25, and

0.375 there is light partly diffracted into the zeroth and the ﬁrst order.

DA1FAGSTEP1S is only on the CD.

Application A3.21.

1. Find the values of n for which the patterns of constructive and destructive

interference are repeating for values of n from 0 to 2. Observe that the path

difference between constructive and destructive interference is λ/2, and the

successive constructive or destructive interference pattern is λ. These length

differences correspond to the length differences produced by H .

3.7. FRESNEL DIFFRACTION 181

2. A lamellar grating is an interferometer with adjustable length H .Itpro-

duces the optical path difference by increasing H in small steps. It is usually

operated in reﬂection and then the length is only 1/2 the length needed to pro-

duce the same optical path difference compared to the case of transmission,

discussed in (1).

FileFig A3.22 (DA2FAGRSTEP2S)

There are four intensity patterns P 1 to P 4, each for a different value of H 1

to H 4. Each two are written for the same wavelength. The values of H 1 and

H 2 have been chosen such that P 1 and P 2 show the constructive interference

pattern for λ1 and λ2, and H 3 and H 4 that P3 and P4 show the destructive

interference pattern for λ1 and λ2.

DA2FAGSTEP2S is only on the CD.

Application A3.22.

1. Get FileFig 3.A2 on the screen and save it. Then modify P 1 to P 4 such that

all H have the same height. Now we can simulate the lamellar grating inter-

ferogram for two wavelengths λ1  0.0005 and λ2  0.0007 by changing

from H  0.00005 in steps of 0.00005 and see how the constructive and

destructive interference patterns change on the observation screen for the

two wavelengths. An interferogram can be obtained by observing the center

and recording the sum of the intensities for the two wavelengths.

2. We go backto FileFig3.A2.The four patterns show constructed and destructed

interference for different settings of the lamellar grating. In other words, all

four patterns using H 1 to H 4 are different. For the two wavelengths, we have

the constructed interference at the center. Destructive interference appears

at different length Y from the center on the observation screen. Since the

detector should only observe the zero order, one has to choose the size such

that the ﬁrst orders are not detected.

3. What is the diameter of the detector area when the smallest wavelength is

λ1  0.

001 and the largest wavelength λ2  0.004?

4. What are the changes of the detector area, when changing a to 2a or

5. What happens when changing N.

APPENDIX 3.2

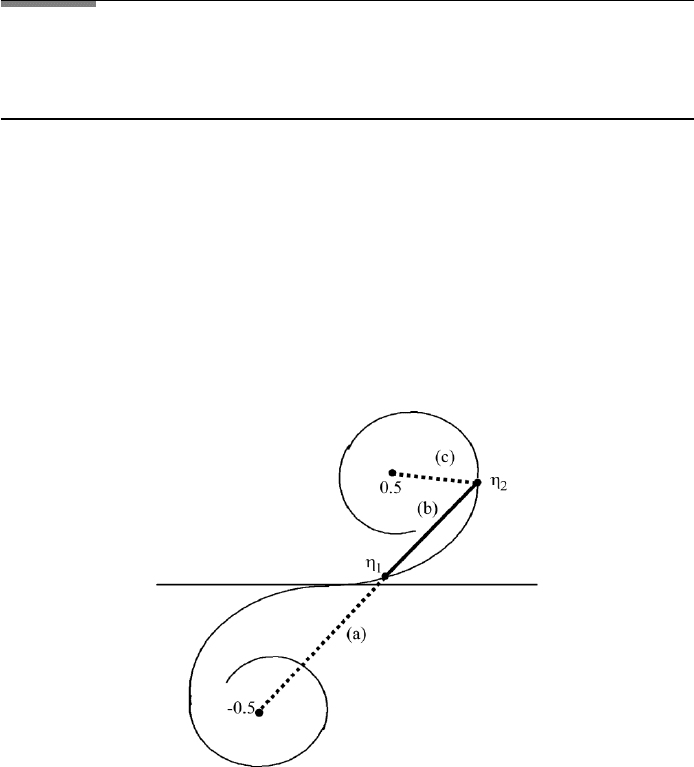
A3.2.1 Cornu’s Spiral

A graph of the Fresnel integrals S versus C is called a Cornu spiral (FileFig

3.A3). One can graphically obtain a diffraction pattern from Cornu’s spiral. As

182

3. DIFFRACTION

an example we discuss the diffraction on a slit. The intensity is given by

I (Y ) {C[η

(Y )] −C[η

(Y )]}

+{S[η

(Y )] −S[η

(Y )]}

(A3.5)

and depends on the points η

(Y ) and η

(Y ), assuming that d, λ, and X are given.

I (Y ) is the square of the geometrical distance on the Cornu spiral between the

points η

and η

. The diffraction pattern is obtained by plotting (distance)

a function of Y for η

and η

. By the division of all values by (distance)

for

Y  0 one can obtain a normalized pattern.

FileFig A3.23 (DA3FECOR)

Graph of S(Y ) as function of C(Y ). This graph is called Cornu’s spiral.

DA3FECOR is only on the CD.

A3.2.2 Babinet’s Principle and Cornu’s Spiral

We consider two complementary screens, I and II. Screen I may just have a hole

and screen II has a stop of the same size as the hole. If added together, no light may

pass. Babinet’s principle tells us that complementary screens generate similar

diffraction patterns. In FileFig 3.A3 we have plotted one-half of the Cornu spiral

for η from 0 to ∞. Let us consider a slit and the complementary screen, a stop of

the same width. The diffraction pattern of screen I for one point Y is obtained by

measuring the length between the corresponding points η

and η

(as discussed

FIGURE A3.30 Cornu’s spiral. The line(b) corresponds to the diffraction pattern of a slit and (a)

and (c) of a stop.

3.7. FRESNEL DIFFRACTION 183

above) which we call length (b) (see Figure A3.30). The diffraction pattern of

screen II may be obtained by using the distances (a) from −∞ to η

and (c)

from η

to ∞. If we want to get the diffraction pattern on a different point Y , the

points η

and η

are displaced in correspondence with the choice of the Y -value

and will affect the diffraction pattern for both screens in the same way.

The distances (a) and (c) and the distance (b) from η

to η

represent the

diffraction pattern for the addition of the two complementary screens for which

no diffraction pattern can be observed.

See also on CD

PD1. Diffraction on a Slit and Width of Diffraction Pattern (see p.1 40).

PD2. Diffraction on a Slit and the ﬁrst Maxima (see p. 141).

PD3. Rectangular Aperture (see p. 145).

PD4. Circular Aperture, ﬁrst Minimum (see p. 149).

PD5. Circular Aperture, Comparison with Slit (see p. 149).

PD6. Double Slit (see p. 153).

PD7. Grating at Normal Incidence (see p. 153).

PD8. Amplitude Grating (see p. 156).

PD9. Echelette Grating (see p. 158).

PD10. Resolution depending on N and d/a ratio (see p. 162).

PD11. Grating Resolution (see p. 163).

PD12. Babinet’s Principle (see p. 166).

PD13. Fresnel and Far Field Diffraction of a Slit and round Aperture (see p.

173).

PD14. Fresnel Diffraction on an Edge (see p. 175).

CHAPTER

Coherence

4.1 SPATIAL COHERENCE

4.1.1 Introduction

In the chapter on interference, we always considered only one incident wave

and assumed that it was emitted by a distant point source. Recalling Young’s

experiment, the incident wave generated two new waves at the two openings at

distance a of a double slit screen. The two new waves had a ﬁxed phase relation

and their superposition generated the interference pattern. The two waves were

called coherent waves. In our model description we used two monochromatic

waves with a ﬁxed phase relation. The superposition generated the amplitude

interference pattern, and the corresponding intensity pattern could be related to

observations.

In this chapter we study waves emitted independently from several distant

sources and assume that there is no ﬁxed phase relation among them. Using for

the analysis the double slit aperture of Young’s experiment, one may observe an

intensity interference pattern for speciﬁc distances of the source points between

them. However, one may also choose other speciﬁc distances, and one will not

ﬁnd an intensity interference pattern. It is common to call the light of the same

sources “spatially coherent" when an intensity interference pattern is observed

and “spatially incoherent" when the intensity interference pattern disappears.

4.1.2 Two Source Points

Let us look at a double star, where each star emits its light independently of

the other. The waves of both are incident on a screen of two slits of width d

and separation a of Young’s experiment. In Figure 4.1, this is shown (without

diffraction) for one source point S

positioned on the axis and for a second source

point S

at distance s from the ﬁrst.

185

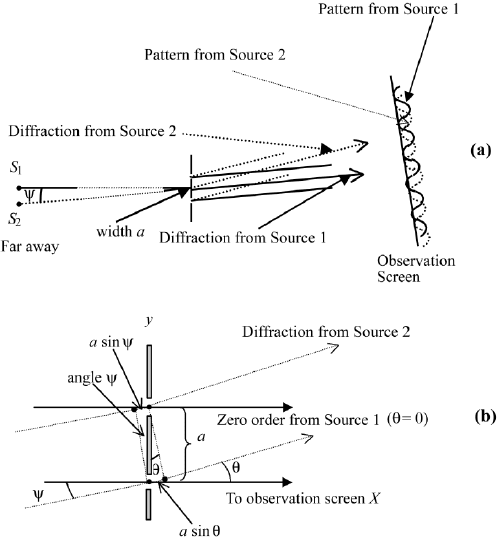
186 4. COHERENCE

FIGURE 4.1 (a) Superposition of two of Young’s experiments using separate sources S

and S

The distance between the sources is s and both “use” the same separation a of the double slit. The

distance from the sources to the aperture is Z, and to the observation screen is X; (b) light from

has the angle ψ with the axis and is diffracted into the angle θ.

For each source point we have an intensity diffraction pattern and for the two

source points we look at the superposition of two intensity patterns. We assume

in our model calculation that each source point generates a monochromatic wave

of wavelength λ and both are incident on the double slit aperture. The light from

source point S

produces on the observation screen the intensity

I (θ,0)  I

{sin[(πd/λ) sin θ]/[(πd/λ) sin θ ]}

{cos[(πa/λ) sin θ]}

, (4.1)

where θ is the diffraction angle and Io is the normalized intensity. Equation

(4.1) is obtained from the discussion of the double slit (Chapter 3, FileFig 3.10).

For source point S

, the axis of the double slit experiment is rotated by the

angle ψ around the point at the center between the two openings. As a result, the

diffraction angle is counted from the new axis and we have to use d(sin θ −sin ψ)

and a(sin θ −sin ψ) in the diffraction and interference factors of Equation (4.1),

respectively. For the intensity of the light from point S

we have

I (θ,ψ)  I

{sin[(πd/λ)(sin θ − sin ψ)]/[(πd/λ)(sin θ −sin ψ)]}

·{cos[(πa/λ)(sin θ − sin ψ)]}

. (4.2)

4.1. SPATIAL COHERENCE 187

The calculation of the optical path difference is similar to the calculation of the

optical path difference for a grating, illuminated under an angle to the normal

(see Chapter 3, Eq. (3.61)). In this model of spatial coherence, monochromatic

light from each point source uses the same double slit aperture and generates an

intensity fringe pattern. The waves from each source point have no ﬁxed phase

relation between each other and each produces an intensity fringe pattern of

its own. The intensities of these two fringe patterns are superimposed. Whether

fringes can be observed depends not only on the separation s (and consequently

on ψ) and the wavelength, but also on the separation a of the two slits in the

double slit arrangement. However, this separation “a” is assumed to be constant.

In FileFig 4.1 we calculate the superposition of the intensity pattern depending

on the separation of the two source points. The separation s is taken in “common

length units” as discussed in Chapter 1. The ﬁrst graph shows the intensity

interference pattern for both source points at the same spot, that is, for s  0.

The second graph showsthe reduced interference pattern for the distance between

the two source points of s  1.5. The third graph shows the disappearance of

the intensity pattern at the distance of s  2.25 and the fourth graph shows the

reappearance at s  2.6. We see that the superposition of the intensity pattern,

produced by the two sources with incoherent light, cancel for the speciﬁc distance

between the two source points of s  2.25.

When fringes are observed of the superposition of the two intensity fringe

patterns, one calls the light producing the fringe pattern spatially coherent. When

no fringes are observed, the light is called spatially incoherent.

FileFig 4.1 (C1COH2S)

Graphs are shown for the superposition of the intensities I (θ,0) and I (θ,ψ) for

two point sources at variable distances s as a function of the angle θ. Parameters

used are the separation of the two openings a  1 mm, opening of the slits

d  0.05mm, wavelength λ  0.0005 mm, distance from source to double slit

Z  9000 mm, and distance from aperture to observation screen X  4000 mm.

Four distances are used, s  0, s  1.5mm, s  2.25mm, and s  2.6mm, of

separation s  Zψ of the two source points, corresponding to four values of

ψ. Fringe patterns are observed for separations s smaller than 2.25 mm. For

a ·ψ  λ/2, that is for s  2.25 mm, we have for the ﬁrst time disappearance of

fringes; that is, the maxima of I(θ,ψ) are at the minima of I(θ,0).Fors larger

than 2.25 mm the fringe pattern reappears.