Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple

Подождите немного. Документ загружается.

208 5. MAXWELL’S THEORY

and obtain

 E

exp i{kx sin φ + kz cos φ − 2πt/T} (5.11)

For the general case of E and B propagating in three dimensions one gets

E  E

exp i{k(n

x +n

y +n

z) −ωt} (5.12)

and

B  B

exp i{k(n

x +n

y +n

z) −ωt}.

5.2.2 The Superposition Principle

The superposition principle is an important principle in physics. Adding n

solutions of the wave equations we may write

E(x, y, z, t) 



(x,y,z,t). (5.13)

Since the wave equation is a linear second-order differential equation and the

(x,y,z,t) are solutions to it, it follows that E(x, y, z,t) is also a solution.

5.3 DIFFERENTIATION OPERATION

Inserting E and B into Maxwell’s equations, one ﬁnds, the following as a result

of differentiation with respect to time and space coordinates.

5.3.1 Differentiation “Time" ∂/∂t

One obtains for operating (∂/∂t) on the function exp i{k(n

x +n

y +n

z)−ωt}:

−iω exp i{k(n

x +n

y +n

z) −ωt}, (5.14)

that is, multiplication by −iω of the exponential function.

5.3.2 Differentiation “Space" ∇i∂/∂x + j∂/∂y + k∂/∂z

Differentiation with respect to x, that is, (∂/∂x) on the function exp i{k(n

x +

y +n

z) −ωt}, results in

ikn

exp i{k(n

x +n

y +n

z) −ωt} (5.15)

and operating with ∇ on the function exp i{k(n

x +n

y +n

z) − ωt} one gets

ikn exp i{k(n

x +n

y +n

z) −ωt}, (5.16)

that is, multiplication by ikn of the exponential function.

5.4. POYNTING VECTOR IN VACUUM 209

The results of differentiation under Sections 5.3.1 and 5.3.2 may be stated as:

the differentiations of plane wave solutions of E and B with respect to time or

space coordinates are equivalent to multiplications by

Time coordinate: (∂/∂t) →−iω

Space coordinate: ∇→ikn.

Substitution of these operations into the set of Maxwell’s equations for a vacuum

results in

kn × E  iωB (5.17a)

kn × B −iωE (5.17b)

kn · E  0 (5.17c)

kn · B  0. (5.17d)

From Eq. (5.17a) and (5.17b) one sees that the vectors n, E, and B form a mutual

orthogonal triad. Since n points into the direction of propagation, E and B are

perpendicular to n and vibrate perpendicular to each other and to the direction of

propagation.The ﬁeld vectors E and B are both transverse waves (see Eqs. (5.17c)

and (5.17d)) and have no component in the direction of propagation. Forthe phase

velocity ω/k, we obtain c for the wave traveling in a vacuum. The components

of E and B are related by

|B|(1/c)|E|. (5.18)

5.4 POYNTING VECTOR IN VACUUM

The Poynting vector S is deﬁned as the time rate of ﬂow of electromagnetic

energy per unit area

S  ε

E × B  (1/µ

)E × B. (5.19)

We have in MKS units: watts per square meter. The direction of the Poynting

vector is parallel to the wave vector kn. If one takes E in the x direction and B

in the y direction, the vector product of Eq. (5.19) is in the z direction

S  k(1/µ

cos

{k(n

x +n

y +n

z) −ωt}, (5.20)

where we used

E  iE

cos{k(n

x +n

y +n

z) −ωt}

and

B  jB

cos{k(n

x +n

y +n

z) −ωt}.

In the case of vacuum one has B

 (1/c)E

and gets

S  k(1/cµ

cos

{k(n

x +n

y +n

z) −ωt}.

210 5. MAXWELL’S THEORY

Since detectors cannot follow a time variation of optical frequencies, the time

average of the cos

function must be used. The integral over one period T , divided

by T , results in 1/2 (see Chapter 2). Therefore, one has for the time average of

the Poynting vector

S(1/2)(1/cµ

. (5.21)

One observes that the ﬂow of energy is proportional to the square of the amplitude

of the electrical ﬁeld vector. Using complex notation, one may write

S  k(1/cµ

exp i{k(n

x +n

y +n

z) −ωt}.

The absolute value of S is calculated from the square root of SS

∗

. As a result the

exponential factor is eliminated and one has

|S|(1/cµ

. (5.22)

Equation (5.21) for the time average carries the factor 1/2, but that factor is

not present when taking the absolute value. However, the ﬂow of energy is still

proportional to the square of the amplitude of the electrical ﬁeld vector. Compare

the factor 1/2 with what has been discussed in Chapter 2 on complex notation

and intensities.

5.5 ELECTROMAGNETIC WAVES IN AN ISOTROPIC

NONCONDUCTING MEDIUM

In the following we consider isotropic materials which do not have an optic axis.

In contrast, in Section 5.7 we discuss birefringent materials which have an optic

axis.

A harmonic wave vibrating in the y direction and propagating in the x direction

may be represented as

 E

cos(2π{x/λ − t/T}). (5.23)

Using k  2π/λ and ω  2πν, where ν is the frequency ν  1/T ,wehave

for the product λν  c, and for the phase velocity ω/k  c. One may write

Eq. (5.23) as

 E

cos(kx − ωt). (5.24)

In an isotropic, nonconductive medium, the phase velocity ω/k is the same in

all directions and is called v. The index of refraction n is deﬁned as n  c/v.

We call the wavelength in the medium λ

and have λ

ν  v. One may write for

the wave in the medium

 E

cos(2πx/λ

− ωt). (5.25)

5.6. FRESNEL’S FORMULAS 211

Since the frequency is the same in vacuum or in the medium, one has ν  c/λ



v/λ

, or the wavelength in the medium λ

 λ(v/c)  λ/n. Therefore we may

also write

 E

cos(2πxn/λ − ωt). (5.26)

As the refractive index n is always larger than one, the wavelength λ in vacuum

is reduced to λ

 λ/n in the medium. (Also see “optical path difference" in

Chapters 2 and 3.) For harmonic waves, the proportionality of B and E changes

from Eq. (5.18) for a vacuum to

|B|(1/v)|E|(n/c)|E|. (5.27)

Consequently the Poynting vector S has for this case the average value

S(1/2)(n/cµ

(5.28)

and the absolute value is

|S|(n/cµ

. (5.29)

5.6 FRESNEL’S FORMULAS

5.6.1 Electrical Field Vectors in the Plane of Incidence

(Parallel Case)

We consider an interface in the X–Z plane of two nonconducting isotropic media

with refractive indices n

and n

. A wave is incident on the interface and we

assume that its electrical ﬁeld vector E vibrates in the plane of incidence,



 E

o

exp i(k(n · r) − ωt), (5.30)

and its magnetic ﬁeld vector is perpendicular to the plane of incidence,

⊥

 B

⊥o

exp i(k(n · r) − ωt). (5.31)

The propagation vector kn is in the plane of incidence and in our coordinate

system, B

⊥

is in the Z direction. The sign is determined with the right-hand rule

for the triad of n, E, and B. To determine the analytical expression of the exponent

in Eqs. (5.30) and (5.31), the unit vectors n

, n

, and n

, pointing in the direction

of propagation of the incident, reﬂected, and transmitted light (Figure 5.2), are

calculated as

 (n

· i) i + (n

· j) j (5.32)

 (n

· i) i + (n

· j) j (5.33)

 (n

· i) i + (n

· j) j (5.34)

212 5. MAXWELL’S THEORY

FIGURE 5.2 Coordinates for the derivation of Fresnel’s formulas for the case where the electrical

ﬁeld vectors are parallel to the plane of incidence.All magnetic ﬁeld vectors point in the Z direction.

The choice of the direction of the E vectors is such that for normal incidence E

and E

point in

the opposite direction (Born and Wolf convention).

and for the dot products one gets

· i)  sin θ

(5.35)

· j) −cos θ

· j)  cos θ

· j) −cos θ

. (5.36)

The incident wave, using n

(Xi + Y j) may be written as

 E

exp i[k

(sin θ

i −cos θ

j) · (Xi +Y j) − ωt]. (5.37)

After calculating the dot products and proceeding similarly for the reﬂected and

transmitted components of the electrical ﬁeld E

and E

, we list all components

 E

exp i{k

(sin θ

X − cos θ

Y ) −ωt} incident (5.38)

 E

exp i{k

(sin θ

X + cos θ

Y ) −ωt} reﬂected (5.39)

 E

exp i{k

(sin θ

X − cos θ

Y ) −ωt} transmitted, (5.40)

where k

 2πn

/λ and k

 2πn

/λ. The refractive index n

is the refractive

index of the medium of the incident and reﬂected waves, and n

the refractive

index of the medium of the transmitted wave. Note that both are refraction indices

and not components of the vector n.

The boundary condition of electromagnetic theory for a dielectric interface

requires that the tangential component of the ﬁeld vectors E and B are continuous.

We have to take the amplitudes of the incident and reﬂected wave and set it equal

5.6. FRESNEL’S FORMULAS 213

to the amplitude of the transmitted wave. (This should not be confused with

energy conservation, which is when the intensity of the incident wave is equal to

the intensity of the reﬂected plus transmitted wave.) The ﬁeld components E

, and E

are not parallel to the X-axis and their directions have been chosen

similar to those by Born and Wolf (II Ed. 1964, p.38–41). To apply the boundary

conditions, one has to use the projections on the X-axis (see Figure 5.2), and has

for Y  0, using Eqs. (5.38) to (5.40),

cos θ

exp i[k

(sin θ

X) − ωt] − cos θ

exp i[k

(sin θ

X) − ωt]

 cos θ

exp i[k

(sin θ

X) − ωt]. (5.41)

This has to be true for all times; that is,

sin θ

 k

sin θ

 k

sin θ

. (5.42)

As a result one has the law of reﬂection,

 θ

, (5.43)

and with k

 2πn

/λ and k

 2πn

/λ, the law of refraction,

sin θ

 n

sin θ

. (5.44)

We therefore have to consider

cos θ

− cos θ

 cos θ

. (5.45)

Since E

and E

are unknowns, we need a second equation to determine their

values. This can be obtained from the applications of the boundary conditions

to the magnetic ﬁeld vectors B

⊥

. The three vectors perpendicular to the plane

of incidence B

, B

, which correspond to E

, E

, and E

, all point in the Z

direction (Figure 5.2). The phase of the three B vectors is the same as it was for

the three E vectors. The application of the boundary condition results in

+ B

 B

(5.46)

From Eq. (5.27), one has B  (1/v)E. For a medium with refractive index

v  c/n one has B  (n/c)E. Insertion into Eq. (5.46) results in

+ n

 n

. (5.47)

Dividing Eqs. (5.45) and (5.47) by E

, which normalizes by the magnitude of

the incident wave, and calling the reﬂected amplitude r



 E

, and the

transmitted amplitude t



 E

, one has two equations for r



and t



cos θ



+ cos θ



+cos θ

(5.48)

and



− n



−n

. (5.49)

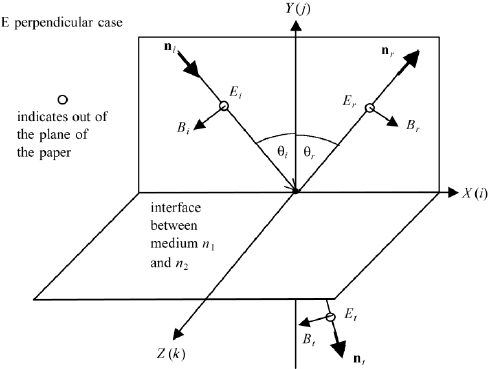
214 5. MAXWELL’S THEORY

FIGURE 5.3 Coordinates for the derivation of Fresnel’s formulas for the case where the electrical

ﬁeld vectors are perpendicular to the plane of incidence. All electrical ﬁeld vectors point in the

Z direction. The choice of direction of the B vectors is such that for normal incidence B

and B

point in the opposite direction (but E

and E

are parallel; Born and Wolf convention).

Renaming θ, both the angle of incidence θ

and the angle of reﬂection θ

, and

calling the angle of refraction θ

 θ



, we solve Eqs. (5.48) and (5.49) for r



and t



(FileFig 5.1):



 (n

cos θ − n

cos θ



)/(n

cos θ + n

cos θ



) (5.50)



 (2n

cos θ )/(n

cos θ + n

cos θ



). (5.51)

These are Fresnel’s formulas for the case where the E vector of the incident light

is in the plane of incident, called the parallel case, the TM-case, or p-polarization.

5.6.2 Electrical Field Vector Perpendicular to the Plane of

Incidence (Perpendicular Case)

In Figure 5.3, we show E

, E

, and E

pointing out of the plane of incidence,

parallel to the Z-axis. The corresponding magnetic ﬁeld vectors B

, B

, and B

are

also indicated. They are in the plane of incidence and need to be projected onto

the X-axes. Similar to the discussion above, after application of the boundary

conditions, we have for the magnetic ﬁeld vectors,

−cos θ

+ cos θ

−cos θ

, (5.52)

or, rewritten using the electrical ﬁeld vector,

−n

cos θ

+ n

cos θ

−n

cos θ

. (5.53)

A second relation is obtained for the electrical ﬁeld vectors

+ E

 E

. (5.54)

5.6. FRESNEL’S FORMULAS 215

We divide Eqs. (5.53) and (5.54) by E

and call E

the reﬂected amplitude

⊥

, and E

the transmitted amplitude t

⊥

.After rearranging the twoequations

for r

⊥

and t

⊥

we have

cos θ

⊥

+ n

cos θ

⊥

+n

cos θ

(5.55)

⊥

− t

⊥

−1. (5.56)

After solving for r

⊥

and r

⊥

one obtains

⊥

 (n

cos θ − n

cos θ



)/(n

cos θ + n

cos θ



) (5.57)

⊥

 (2n

cos θ )/(n

cos θ + n

cos θ



). (5.58)

These are Fresnel’s formulas for the case where the E vector of the incident

light is pointing out of the plane of incidence, called the perpendicular case, the

TE-case,ors-polarization.

FileFig 5.1 (M1FRFOR)

We may use the symbolic operations of a computer program to solve for Fresnel’s

formulas for the p-case (parallel) and s-case (perpendicular).

M1FRFOR is only on the CD.

5.6.3 Fresnel’s Formulas Depending on the Angle of

Incidence

Using the law of refraction, we can eliminate θ



and express Fresnel’s formulas

depending on the angle of incidence. Application of

cosθ





1 − (sin θ



)



(1 − [(n

) sin θ]

results in r

and t

for the parallel (p) case



cos −n



1 − [(n

) sin θ]

)

cos θ + n



1 − [(n

) sin θ]

)

(5.59)



(2n

cos θ )

cos θ + n



1 − [(n

) sin θ]

)

, (5.60)

and r

and t

for the perpendicular (s) case



cos θ − n



1 − [(n

) sin θ]

)

cos θ + n



1 − [(n

) sin θ]

)

(5.61)



(2n

cos θ )

cos θ + n

√

(1 − [(n

) sin θ

)

. (5.62)

216 5. MAXWELL’S THEORY

5.6.4 Light Incident on a Denser Medium, n

, and the

Brewster Angle

5.6.4.1 Phase Shifts

We mentioned in Section 6.1 that we have chosen the sign of the reﬂected electri-

cal vectors at the boundary in the same way as done by Born and Wolf (1964). At

normal incidence, this sign convention results in a negative sign for the reﬂection

coefﬁcient of the p-case. For the s-case there is a positive sign. Since there is no

distinction between the p-case and s-cases for normal incidence, how can this

be explained?

A light wave reﬂected at a denser medium picks up a phase shift of π , and

we may write for the reﬂection coefﬁcients: absolute value times the complex

phase factor; that is, for the p- and s-cases, r

|r

iφ

and r

|r

iφ

respectively. In the book by Born and Wolf (1964) the phase factor for the p-

case is included in r

; that is, for normal incidence φ

 π, e

iφ

−1, and r

is −|r

|.Inthes-case the phase factor is not included; that is φs  0, e

iφ

 1,

and r

is |r

|. Graphs of |r

|, |r

|, φ

, and φ

are shown in FileFig 5.2 for light

incident from a less dense medium to a more dense medium. Note that φ

is the

argument of r

, and φ

of r

5.6.4.2 Brewster’s Angle

In FileFig 5.2 one observes from graphs of r

and r

, depending on the angle of

incidence θ, that for a speciﬁc angle, called the Brewster angle, r

is zero and

is not. From Eq. (5.59) we have for the Brewster angle

cos θ

− n



1 − [(n

) sin θ

]

)  0. (5.63)

We abbreviate a  n

and square Eq. (5.63):

cos

 1 − (sin

)  cos

+ sin

− (sin

) (5.64)

− 1) cos

 (1 − a

−2

)(sin

)  [(a

− 1)/a

] sin

Since a

> 1 we can cancel (a

− 1) and obtain

tan θ

 n

. (5.65)

This is the tangent of the Brewster angle.

FileFig 5.2 (M2FRN2L)

Fresnel’s formulas for n

. Graphs are shown of the absolute value and

the argument of r

, r

, and t

, t

, depending on the angle of incidence θ. The

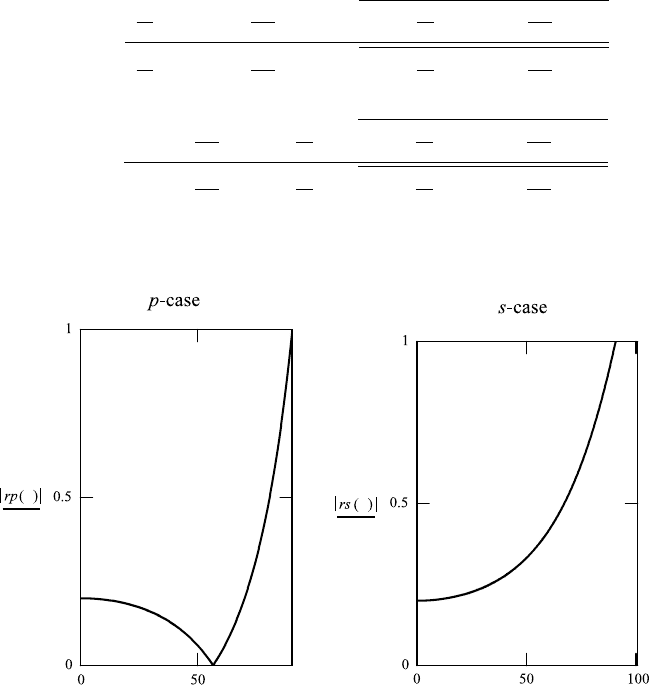
5.6. FRESNEL’S FORMULAS 217

choice of n

 1 and n

 1.5 presents the case for light incident on a material

like glass. At the Brewster angle, one sees that the phase angle changes for

the parallel case from 0 to 180 degrees. For the perpendicular case there is no

Brewster angle and no change. The transmission coefﬁcients are not undergoing

any phase shifts.

M2FRN2L

Amplitudes

Fresnel’s formulas as function of angle of incidence for ﬁrst medium 1, second

medium 2, and n1 <n2.

1. Reﬂection coefﬁcients

Absolute value and imaginary parts for p-case (parallel) and s-case

(perpendicular).

rp(θ):





· cos



2 ·

360

· θ



−



1 −





· sin



2 ·

360

· θ

!





· cos



2 ·

360

· θ





1 −





· sin



2 ·

360

· θ

!

rs(θ):

cos



2 ·

360

· θ



−







1 −





· sin



2 ·

360

· θ

!

cos



2 ·

360

· θ









1 −





· sin



2 ·

360

· θ

!

θ ≡ .1,.2.. 90 n1 ≡ 1 n2 ≡ 1.5.