Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple
Подождите немного. Документ загружается.

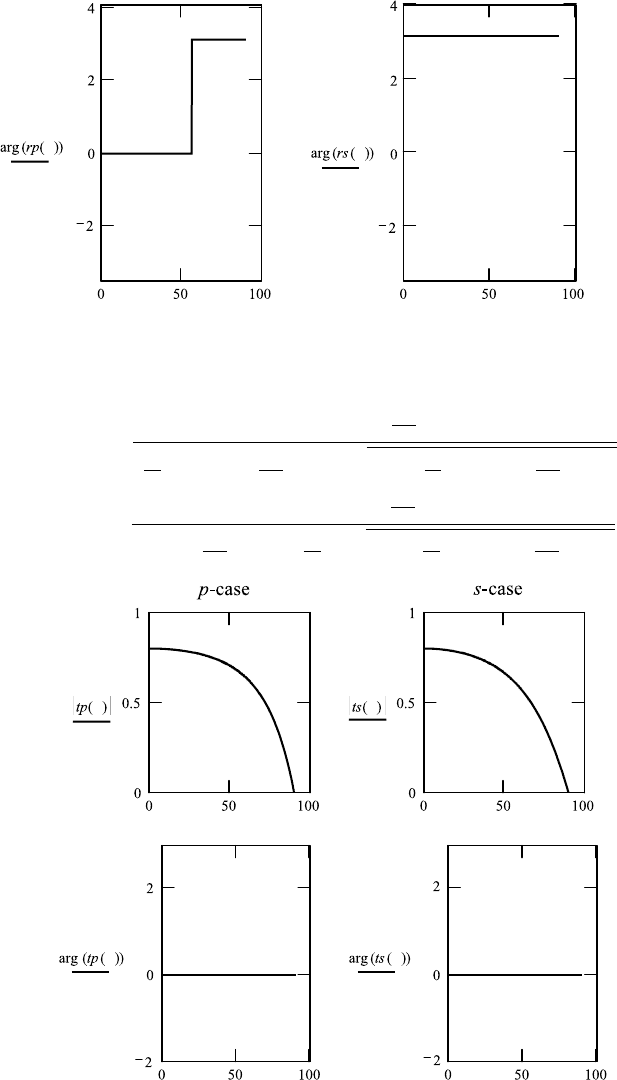
218 5. MAXWELL’S THEORY
q
q
q
q
2. Transmission coefficient
Absolute value and imaginary part for p-case and s-case.
tp(θ):
2 ·cos
2 ·
π
360
· θ
n2
n1
· cos
2 ·
π
360
· θ
+
1 −
n1
n2
· sin
2 ·
π
360
· θ
!
2
ts(θ):
2 ·cos
2 ·
π
360
· θ
cos
2 ·
π
360
· θ
+
n2
n1
·
1 −
n1
n2
· sin
2 ·
π
360
· θ
!
2
q q
q
q
q
q
q
q
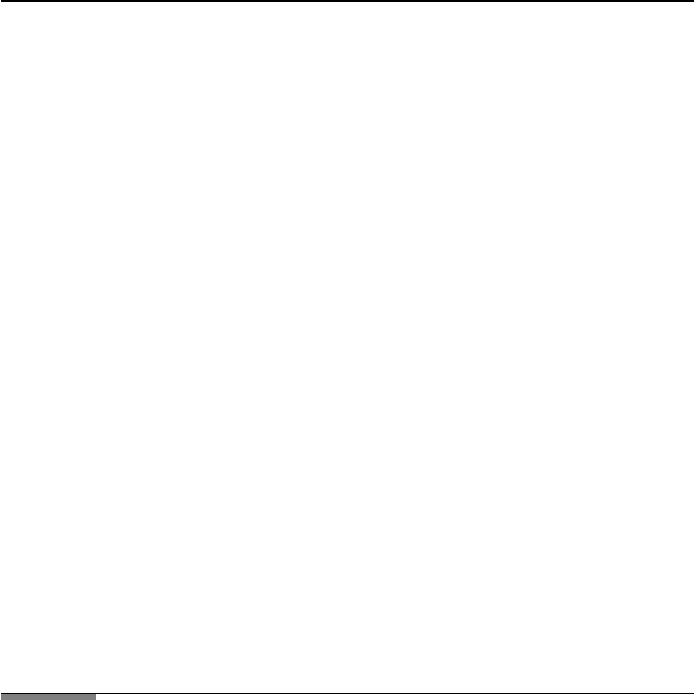
5.6. FRESNEL’S FORMULAS 219
Application 5.2.
1. Study, for a large angle, the changes of the Brewster angle and the slope of
the reflection coefficient. Choose n
1
from a value close to n
2
to values much
smaller than n
2
. Save the case n
1
smaller than n
2
for FileFig 5.4.
2. Make graphs for n
1
1 and n
2
for two different refractive indices. Study
the changes of the argument, the Brewster angle, and the slope of the reflec-
tion coefficient at large angles, that is, at grazing angle incidence. Make the
difference of n
2
and n
2
larger and smaller.
3. Look at the transmission coefficients for the p- and s-cases and plot them on
one graph. Study the difference of the two for different refractive indices n
2
.
5.6.5 Light Incident on a Less Dense Medium, n
1
>n
2
,
Brewster and Critical Angle
5.6.5.1 Brewster Angle
In FileFig 5.3 we have plotted the reflection and transmission coefficients for
light incident on a less dense medium. One sees that the general shape of the
reflection and transmission coefficientsare the same as found for the case n
1
<n
2
discussed in Section 5.6.4, and the Brewster angle is present for the parallel case.
5.6.5.2 Critical Angle and Phase Shifts
At a larger angle than the Brewster angle, called the critical angle θ
c
, the curves
for the absolute value of r
p
and r
s
approach 1, while the transmission coefficients
decrease to 0. All arguments of r
p
and r
s
, and t
p
and t
s
decrease after the critical
angle. We apply the law of refraction to this case and find that the refraction
angle becomes imaginary when the angle of incidence exceeds the critical angle
given by
sin θ
c
n
2
/n
1
, (5.66)
where n
1
is the medium with the larger index of refraction, from which the light
is incident on the interface. The question of real and imaginary refraction angles
is studied in FileFig 5.4.
FileFig 5.3 (M3FRN2S)
Fresnel’s formulas for the case n
1
>n
2
. Graphs are shown of the absolute value
and the argument of r
p
, r
s
, and t
p
, t
s
, depending on the angle of incidence θ.
The choice of n
1
1 and n
2
1.5 presents the case for light incident on a
glasslike material. The Brewster angle appears again for r
p
and for both r
p
and
220 5. MAXWELL’S THEORY
r
s
the critical angle appears. The absolute value of the transmission coefficients
increases before the critical angle and decreases thereafter.
M3FRN2S
Amplitudes
Fresnel’s formulas as function of angle of incidence for first medium 1, second
medium 2, and n1 >n2.
1. Reflection coefficients
Absolute value and imaginary parts for p-case (parallel) and s-case
(perpendicular).
rp(θ):
n2
n1
· cos
2 ·
π
360
· θ
−
1 −
n1
n2
· sin
2 ·
π
360
· θ
!
2
n2
n1
· cos
2 ·
π
360
· θ
+
1 −
n1
n2
· sin
2 ·
π
360
· θ
!
2
rs(θ):
cos
2 ·
π
360
· θ
−
n2
n1
·
1 −
n1
n2
· sin
2 ·
π
360
· θ
!
2
cos
2 ·
π
360
· θ
+
n2
n1
·
1 −
n1
n2
· sin
2 ·
π
360
· θ
!
2
θ ≡ .1,.2.. 90 n1 ≡ 1.5 n2 ≡ 1.
q
q
q
q
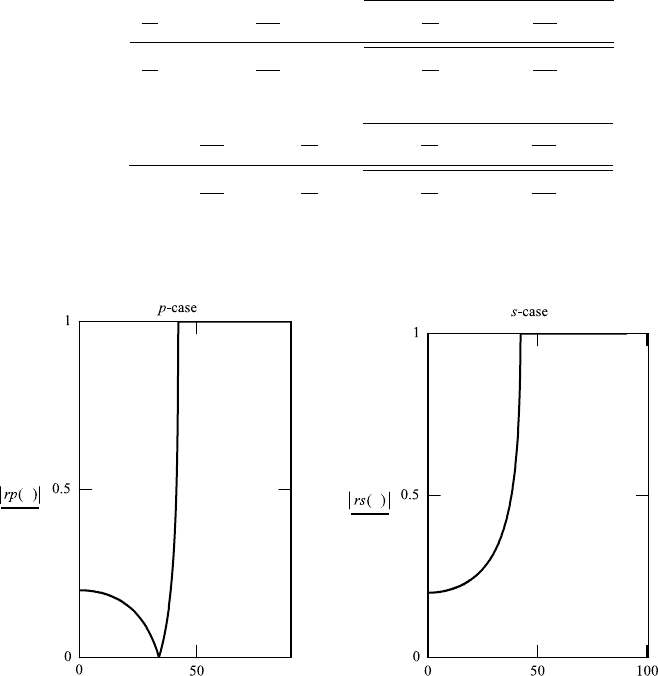
5.6. FRESNEL’S FORMULAS 221
q
q
q
q
2. Transmission coefficient
Absolute value and imaginary part for p- and s-cases.
tp(θ):
2 ·cos
2 ·
π
360
· θ
n2
n1
· cos
2 ·
π
360
· θ
+
1 −
n1
n2
· sin
2 ·
π
360
· θ
!
2
ts(θ):
2 ·cos
2 ·
π
360
· θ
cos
2 ·
π
360
· θ
+
n2
n1
·
1 −
n1
n2
· sin
2 ·
π
360
· θ
!
2
q
q
q
q
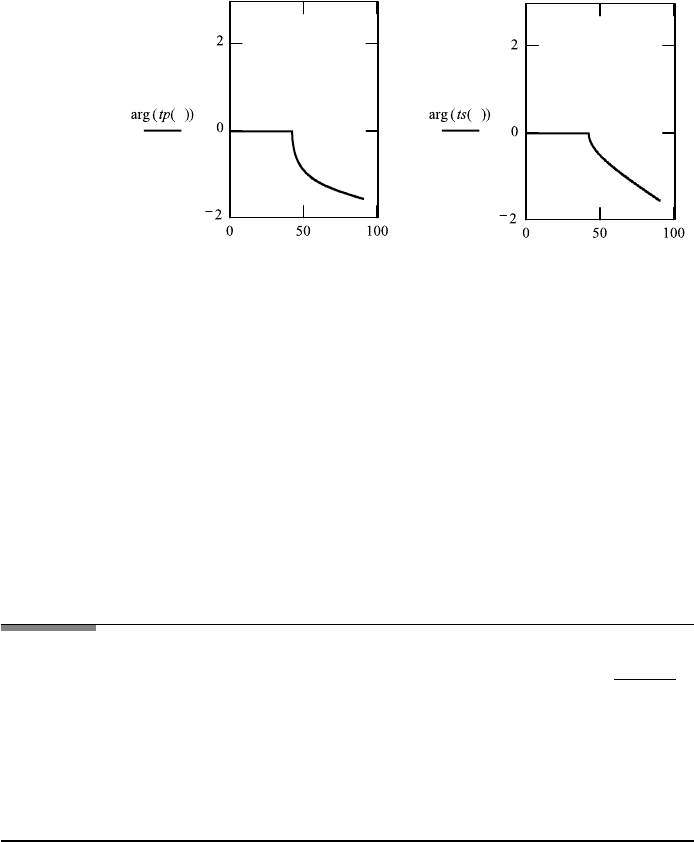
222 5. MAXWELL’S THEORY
q
q
q
q
Application 5.3.
1. Study reflection and transmission coefficients by changing from n
1
>n
2
to
n
1
≈ n
2
and n
1
<n
2
and compare with FileFig 5.2. Observe the different
shape of t
s
and t
p
as they appear in FileFigs.3 and 4. This is an indication
that t
2
s
and t
2
p
are not to be confused with the transmitted intensity.
2. Plot on the same graph, for n 1.5 and two different indices of refraction,
the reflection coefficients and look at the differences of the curves for larger
and smaller differences of the two indices.
3. Change the indices of refraction and observe how the critical angle is
changing.
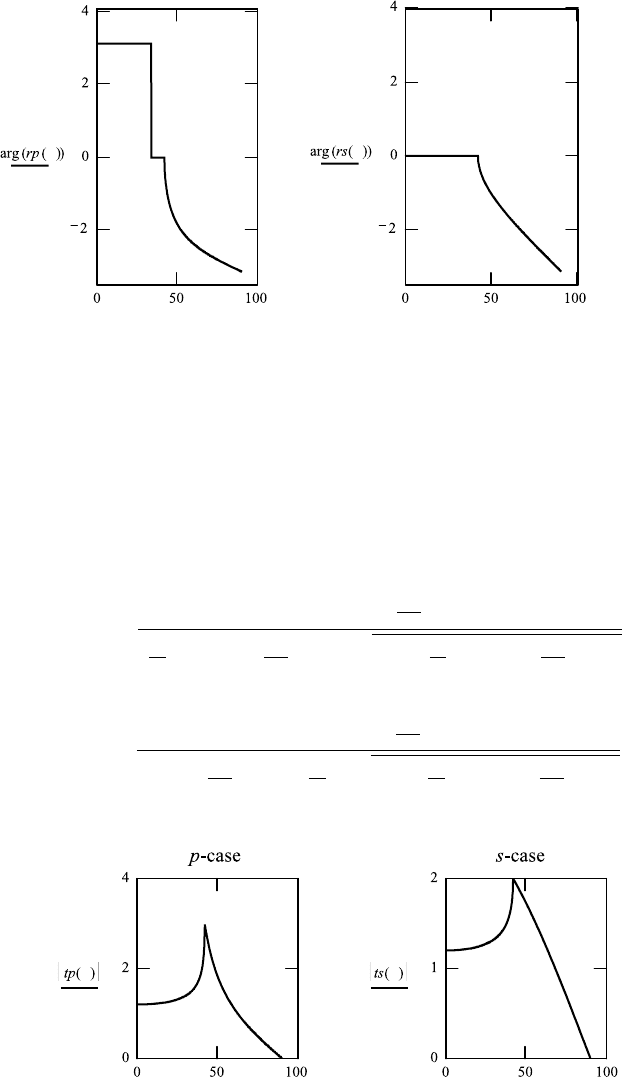
FileFig 5.4 (M4SNELL)
The law of refraction n
1
sin θ
1
n
2
sin θ
2
is plotted as θ
2
(θ
1
) asin
n
1
sin(θ
1
)
n
2
!
:
(1) a graph of θ
2
(θ
1
) for n
1
<n
2
; (2) a graph of θ
2
(θ
1
) for n
1
>n
2
. The
graph ends at the critical angle; and (3) real and imaginary parts, separately
for n
1
>n
2
. One extends from zero to the critical angle, the other from the
critical angle to 90
◦
.
M4SNELL is only on the CD.
5.6.6 Reflected and Transmitted Intensities
In contrast to what was done in the application of the boundary conditions, we
now calculate the energy flow. At the boundary, we equated the sum of the fields
of incident and reflected amplitude on one side with the transmitted amplitude
on the other side. Now we want to find out how much of the incident energy is
reflected and transmitted. From Eq. (5.19) we have for the Poynting vector S for
a vacuum
S ε
0
c
2
E × B (1/µ
0
)E × B. (5.67)
5.6. FRESNEL’S FORMULAS 223
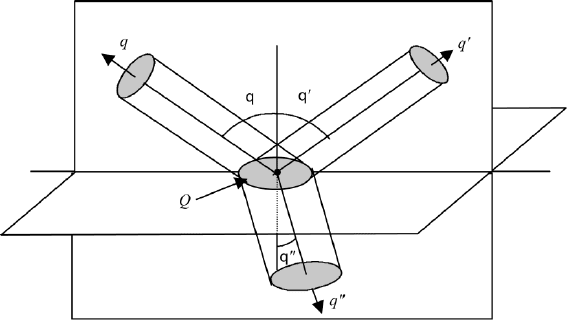
FIGURE 5.4 Areas q, q
, and q
are cross-sections of the power flow of incident, reflected, and
refracted light. Q is the common area at the interface.
For a medium with refractive index n we have with Eq. (5.22) the absolute value
of S,
S (1/µ
0
)E
0
(n/c)E
0
(5.68)
and obtain the time average, similar to Eq. (5.21),
S(1/2)(n/cµ
0
)E
2
0
. (5.69)
Let us call the incident energy per area S
i
, the reflected S
r
, and the refracted
S
t
. In Figure 5.4 we have indicated the areas through which the energy flows.
The area q corresponds to the incident energy and q
and q
to the reflected and
refracted energy, respectively. At the interface we have to use the same area Q
for incident, reflected, and refracted energy and have to multiply S
i
, S
r
, and S
t
by a cosine factor corresponding to the projections of q, q
, q
onto the X–Z
plane. We then have
(1/2)(n
1
/µ
0
c)E
2
io
cos θ
1/2(n
1
/µ
0
c)E
2
ro
cos θ + 1/2(n
2
/µ
0
c)E
2
to
cos θ
. (5.70)
5.6.6.1 The Case n
1
<n
2
We call the reflectance R E
2
ro
/E
2
io
r
2
, where r stands for both the parallel
and perpendicular cases. Using conservation of energy,
R + T 1, (5.71)
we obtain from Eq. (5.70) for the transmittance T ,
T 1 − r
2
(n
2
cos θ
/n
1
cos θ )t
2
, (5.72)
where E
2
to
/E
2
io
and t stands again for both cases.

224 5. MAXWELL’S THEORY
We call (n
2
cos θ
/n
1
cos θ ) α and have, writing the parallel and
perpendicular cases separately,
R
r
2
and T
αt
2
(5.73)
R
⊥
r
2
⊥
and T
⊥
αt
2
⊥
. (5.74)
Energy conservation holds for both cases and by using
T 1 − R (5.75)
one can avoid using the factor α. One can calculate R
and R
⊥
from Fresnel’s
formulas, using the amplitude reflection coefficients, and then use 1−R to obtain
T . In FileFig 5.5 we have plotted R
p
, R
s
, T
p
1 −R
p
and T
s
1 −R
s
for the
case where n
1
<n
2
,from0to90
◦
.
FileFig 5.5 (M5FRINTN2L)
Graphs of R
p
, R
s
, T
p
1 − R
p
, and T
s
1 − R
s
depending on the angle of
incidence for the case where n
1
<n
2
.
M5FRINTN2L
Intensities
Fresnel’s formulas as function of angle of incidence for n1 <n2 for Rp rp
2
,
Rs rs
2
, and Tp 1 − R
p
, Ts 1 − Rs.
1. Amplitude reflection coefficients
rp(θ):
n2
n1
· cos
2 ·
π
360
· θ
−
1 −
n1
n2
· sin
2 ·
π
360
· θ
!
2
n2
n1
· cos
2 ·
π
360
· θ
+
1 −
n1
n2
· sin
2 ·
π
360
· θ
!
2
rs(θ):
cos
2 ·
π
360
· θ
−
n2
n1
·
1 −
n1
n2
· sin
2 ·
π
360
· θ
!
2
cos
2 ·
π
360
· θ
+
n2
n1
·
1 −
n1
n2
· sin
2 ·
π
360
· θ
!
2
n1 ≡ 1 n2 ≡ 1.5 θ ≡ 0,.4..90.
2. Reflection: intensities
Rp(θ): rp(θ)
2
Rs(θ ): rs(θ)
2
.

5.6. FRESNEL’S FORMULAS 225
q
q
q
q
3. Transmission: intensities
Tp(θ): 1 − Rp(θ) Ts(θ): 1 − Rs(θ ).
q
q
q
q
Application 5.5.
1. Make graphs of r
2
p
, r
2
s
, t
2
p
and t
2
s
for the case where n
1
<n
2
. Find which
quantities, just squared, are useful for calculation of corresponding intensi-
ties, and which are not. Compare the graphs of the intensities and find out if

226 5. MAXWELL’S THEORY
R
p
or R
s
are equal to r
2
p
or r
2
s
, and similarly if T
p
or T
s
are equal to t
2
p
or t
2
s
,
respectively.
2. Make a graph of the factor α (n
2
cos θ
/n
1
cos θ ) for n
1
<n
2
and n
1
>n
2
and compare. To do this one has to use the law of refraction to substitute for
cos θ
.
5.6.6.2 n
1
>n
2
, Critical Angle and Total Reflection
From Eqs. (5.59) to (5.62) one sees that the square root in all expressions may
become negative when θ is beyond the critical angle.We may rewritethe formulas
by taking out of the square root the factor
√
−1 i and have all reflection and
transmission coefficients be complex functions. Let us look, as an example, at
the perpendicular case where we have for r,
r
s
cos θ − (n
2
/n
1
)i
[(n
1
/n
2
) sin θ]
2
− 1)
cos θ + (n
2
/n
1
)i
[(n
1
/n
2
) sin θ]
2
− 1)
(5.76)
which we may write with the abbreviations a cos θ and
b n
2
/n
1
[(n
1
/n
2
) sin θ]
2
− 1as
r
⊥
(a − ib)/(a + ib). (5.77)
The complex conjugate is
r
∗
⊥
(a + ib)/(a − ib). (5.78)
To get the reflectance R, one has to take rr
∗
, where r
∗
is the complex conjugate of
r and R r
⊥
r
∗
⊥
1, and it follows that T 0. For all angles of incidence equal
to or larger than the critical angle we have total reflection; that is, R
R
⊥
1
and T
T
⊥
0. In FileFig 5.6 we have plotted R
, R
⊥
, T
, and T
⊥
for n
1
1.5,
n
2
1 and θ from0to90
◦
.
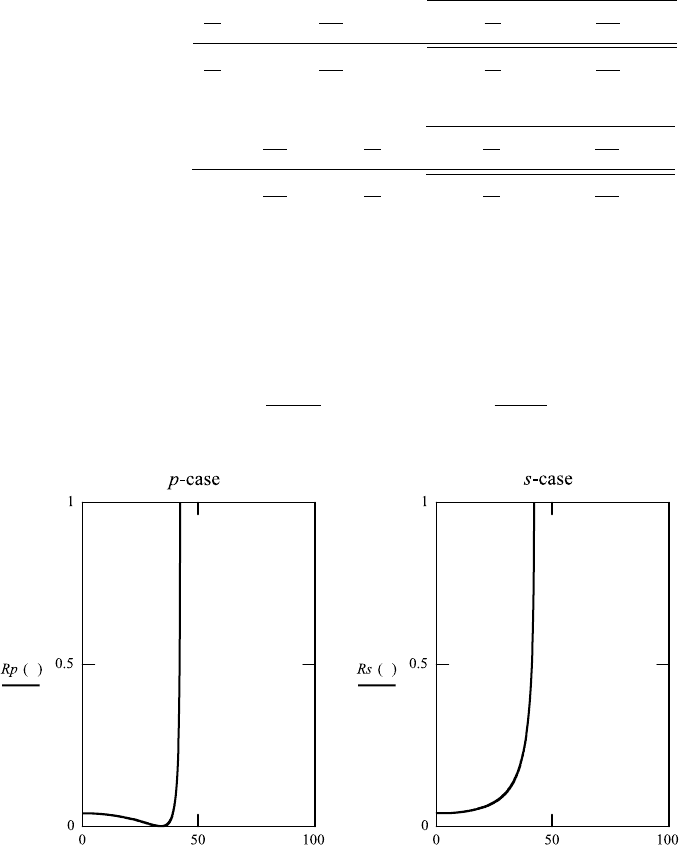
FileFig 5.6 (M6FRINTN2S)
Graphs of R
p
, R
s
, T
p
1 − R
p
, and T
s
1 − R
s
depending on the angle of
incidence for the case where n
1
>n
2
.
M6FRINTN2S
Intensities
Fresnel’s formulas as function of angle of incidence for n1 >n2 for Rp rp
2
,
Rs rs
2
, and Tp 1 − Rp, Ts 1 − Rs.
5.6. FRESNEL’S FORMULAS 227
1. Amplitude reflection coefficients
rp(θ):
n2
n1
· cos
2 ·
π
360
· θ
−
1 −
n1
n2
· sin
2 ·
π
360
· θ
!
2
n2
n1
· cos
2 ·
π
360
· θ
+
1 −
n1
n2
· sin
2 ·
π
360
· θ
!
2
rs(θ):
cos
2 ·
π
360
· θ
−
n2
n1
·
1 −
n1
n2
· sin
2 ·
π
360
· θ
!
2
cos
2 ·
π
360
· θ
+
n2
n1
·
1 −
n1
n2
· sin
2 ·
π
360
· θ
!
2
n1 ≡ 1.5 n2 ≡ 1 θ ≡ 0,.01.. 90.
2. Reflection: intensities
Rp(θ): rp(θ)
·rp(θ) Rs(θ ): rs(θ)·rs(θ).
q
q
q
q
3. Transmission: intensities
Tp(θ): 1 − Rp(θ) Ts(θ): 1 − Rs(θ ).
