Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple
Подождите немного. Документ загружается.

238 5. MAXWELL’S THEORY
yy1(x1) : b · sin
−2 ·π ·
x1
360
yy2(x2) : b · sin
−2 ·π ·
x2
360
yy3(x3) : b · sin
−2 ·π ·
x3
360
yy4(x4) : b · sin
−2 ·π ·
x4
360
.
Application 5.9. Modify the four graphs to plot left and right polarized light on
the same graph.
5.7.6 Crossed Polarizers
The experimental setup of crossed polarizers is a sequence of a horizontal (X
direction) and a vertical (Y direction) polarizer. Any light passin the first polar-
izer will not pass the second. Therefore no light passes the crossed polarizers
configuration.
5.7.6.1 Half Wave Plate Between Crossed Polarizers
We next discuss the case where a half-wave plate is placed between the polarizer
and analyzer of the crossed polarizers configuration. We assume that the half
wave plate is oriented with its optical axis (Z)at45
◦
degrees to the horizontal
direction of the polarizer (Figure 5.11). The incident light is first horizontally
polarized by the polarizer and then incident on the half wave plate. The horizontal
polarized light is split up in a Z component along the axis of the half-wave plate

5.7. POLARIZED LIGHT
239
FIGURE 5.11 Half-wave plate between crossed polarizers. The horizontal polarized light is rep-
resented by the two perpendicular vectors E
Y
and E
Z
. The half-wave plate turns E
Z
into −E
Z
.
The resultant of E
Y
and −E
Z
is polarized in the vertical direction and may pass the analyzer.
and a Y component perpendicular to it. The Z component leaves the plate with a
phase shift of π , oscillating in the Z direction, while the Y component remains
oscillating in the Y direction. The resultant of the two components leaving the
half-wave plate is polarized in the vertical direction, and will pass the vertical
polarizer. In this setup all the light passing the horizontal polarizer will also pass
the vertical polarizer, sometimes called the analyzer.
5.7.6.2 Quarter-Wave Plate Between Crossed Polarizers
A quarter-wave plate is placed between crossed polarizers with its axis at 45
◦
(Figure 5.12). The light passing the first polarizer, incident on the quarter-wave
plate, is decomposed into two components. One oscillates parallel and the other
perpendicular to the axis of the quarter wave plate. The resultant, leaving the
quarter-wave plate, is not stationary. It rotates around the direction of propagation
X and light passes the second polarizer, also called the analyzer. Rotation of the
quarter wave plate around a range of angles will not affect this. However, the
axis of the quarter-wave plate should not be parallel to the linear polarizers.
FIGURE 5.12 A quarter-wave plate between polarizers.

240 5. MAXWELL’S THEORY
5.7.7 General Phase Shift
5.7.7.1 Half- and Quarter-Wave Plates
We have discussed the generation of phase differences of π and π/2 by a half-
wave plate and a quarter-wave plate. Another way to produce a phase difference
between the two components of the electrical field vector is by internal total
reflection. In the case of n
1
>n
2
, we have complex reflection coefficients in the
region of total reflection. The range of the phase shifts is between plus or minus
π, different for the p- and s-cases. We also have a change in the magnitude of
reflection. If we superimpose the vectors of the total internal reflected light for
the p- and s-cases, we would, in general, obtain elliptical polarized light.
5.7.7.2 Linear, Circular, and Elliptical Polarized Light
We now examine elliptically polarized light. We consider the plane X L and
the corresponding phase difference of φ
X
, for angles between 0 and 360
◦
.We
refer to Eqs. (5.89) and (5.90):
E
Y
jA exp i(k
1
L − ωt) (5.89)
E
Z
kA exp i(k
1
L − ωt + φ
X
). (5.90)
By only using the real part of the Y and Z components and substituting α
(k
1
L − ωt), we have
E
Y
A cos α (5.101)
E
Z
A cos(α + φ) A[cos α cos φ − sin α sin φ]. (5.102)
Eliminating α, the equation of an ellipse is obtained:
E
2
Z
− 2E
Y
E
Z
cos φ + E
2
Y
A
2
sin φ
2
. (5.103)
In FileFig 5.10 we show that one may write Eq. (5.103) in matrix form and that
we have for φ 0, linearly polarized light,
E
Y
E
Z
, (5.104)
for φ π/4, elliptically polarized light, and have the equation of an ellipse,
E
2
Z
/(1 − 1/
√
2) + E
2
Y
/(1 + 1/
√
2) 1, (5.105)
and for φ π/2, circular polarized light, and have the equation of a circle,
E
2
Z
+ E
2
Y
1. (5.106)
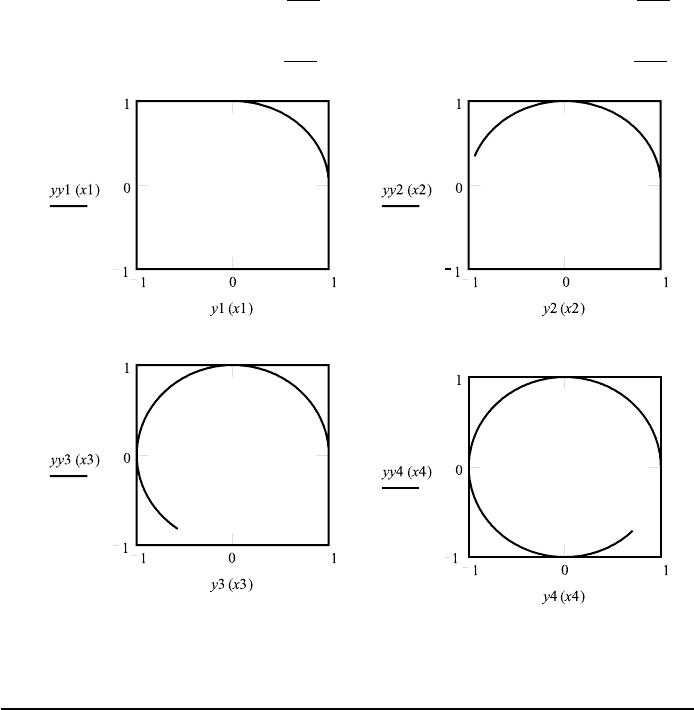
FileFig 5.10 (M10POELIPSES)
The general equation of the ellipse is shown in vector-matrix notation, using
the eigenvalue method. The equations are obtained for φ 0 (linear polarized
5.7. POLARIZED LIGHT 241
light) for φ π/4, (elliptically polarized light), and φ π/2 (circularpolarized
light).
M10POELIPSES is only on the CD.
Application 5.10. Derive the equations for φ 3π/4, φ 5π/2, π 3π/2,
and φ 7π/4 and compare with results of FileFig 5.11.
In Appendix A5.2 we show that the rotation of the coordinate system may be
equivalent to a transformation to principal axes. In FileFig 5.11 we show graphs
of one component plotted against the other for
φ 0,φ π/4,φ π/2,φ 3π/4,
φ π, φ 5π/4,φ 3π/2,φ 7π/4,
φ 2π
. (5.107)
One sees that the two components of linearly polarized light, vibrating along
perpendicular directions, result in linear polarized light when the phase difference
is φ
X
0, π , and 2π. The resulting vibration takes place along a line tilted by
45
◦
for φ
X
0, 2π, and tilted by 135
◦
for φ
X
π.Forφ
X
π/2 we have left
circular polarized light and for φ
X
3π/2, equivalent to −π/2, right circular
polarized light. The ellipse is left turning, when the φ
X
values are first larger and
then smaller than φ
X
π/2, and “right turning" for φ
X
values first larger and
then smaller than φ
X
3π/2. The large axis of the ellipse is always oriented in
the same direction as the axis of the “closest" linear polarized light.
FileFig 5.11 (M11POELIPLIS)
Graphs are shown of the equation of the ellipse, that is, Eq. (5.103) for φ 0,
φ π/4, φ π/2, φ 3π/4, φ π, φ 5π/4, φ 3π/2, φ 7π/4, and
φ 2π.
M11POELIPLIS
Elliptical Polarized Light
Similarly to that discussed in FileFig 5.9 we plot cos(−2πx/360) on the z-axis
and cos(−2πx/360 +) on the y-axis.
x ≡ 1, 2.. 360 φ1: 0
y1(x): cos
−2 ·π ·
x
360
yy1(x): cos
−2 ·π ·
x
360
+ φ1
φ2:
π
4
242 5. MAXWELL’S THEORY
y2(x): cos
−2 ·π ·
x
360
yy2(x): cos
−2 ·π ·
x
360
+ φ2
φ3:
π
2
y3(x): cos
−2 ·π ·
x
360
yy3(x): cos
−2 ·π ·
x
360
+ φ3
φ4: 3 ·
π
4
y4(x): cos
−2 ·π ·
x
360
yy4(x): cos
−2 ·π ·
x
360
+ φ4
φ5: π
y5(x): cos
−2 ·π ·
x
360
yy5(x): cos
−2 ·π ·
x
360
+ φ5
φ6:
5 · π
4
y6(x): cos
−2 ·π ·
x
360
yy6(x): cos
−2 ·π ·
x
360
+ φ6
φ7:
3 · π
2
y7(x): cos
−2 ·π ·
x
360
yy7(x): cos
−2 ·π ·
x
360
+ φ7
φ8: 7 ·
π
4
y8(x): cos
−2 ·π ·
x
360
yy8(x): cos
−2 ·π ·
x
360
+ φ8
APPENDIX 5.1
A5.1.1 Wave Equation Obtained from Maxwell’s Equation
∇×E −∂B/∂t
c
2
∇×B +∂E/∂t (A5.1)
∇·E 0
∇·B 0.
From the first equation of A5.1 we have by taking the cross product with ∇
∇×∇E −∂/∂t∇×B (A5.2)
and using the identity
∇×∇×E ∇(∇·E) −∇
2
E (A5.3)
we get
∇(∇·E) −∇
2
E −∂/∂t∇×B. (A5.4)
5.7. POLARIZED LIGHT 243
Inserting the second equation of Eq. (A5.1), we obtain
∇(∇·E) −∇
2
E −(1/c
2
)∂/∂t(∂E/∂t). (A5.5)
With ∇·E 0 of the third equation of (A5.1) we have the vector wave equation
for the electrical field vector E,
∂
2
E/∂x
2
+ ∂
2
E/∂y
2
+ ∂
2
E/∂z
2
(1/c
2
)∂
2
E/∂t
2
. (5.3)
Using a similar formalism we derive the vector wave equation for the magnetic
field vector B,
∂
2
B/∂x
2
+ ∂
2
B/∂y
2
+ ∂
2
B/∂z
2
(1/c
2
)∂
2
B/∂t
2
. (5.4)
A5.1.2 The Operations ∇ and ∇
2
Cartesian coordinates (x,y,z)
∇i∂/∂x + j∂/∂y + k∂/∂z
∇
2
∂
2
/∂x
2
+ ∂
2
/∂y
2
+ ∂
2
/∂z
2
Spherical coordinates (r, θ , φ)
∇i∂/∂r + j(1/r)∂/∂θ +k(1/r sin φ)∂/∂φ
∇
2
(1/r
2
)∂/∂r(r
2
∂/∂r)
+ [1/(r
2
sin θ)]∂/∂θ(sin θ ∂/∂θ) + [1/(r
2
sin
2
θ)]∂
2
∂φ
2
APPENDIX 5.2
A5.2.1 Rotation of the Coordinate System as a Principal
Axis Transformation and Equivalence to the Solution
of the Eigenvalue Problem
FileFig A5.12 (MA2ROTMAS)
1. Rotation matrices and their multiplication.
2. Demonstrated that the equation of the ellipse is obtained without cross terms
when introducing φ π/4.
a. Introduction of φ π/4 into the general equation of the ellipse
b. Introduction of φ π/4 as rotation angle
If the value of φ π/4 is not known, it may be determined from the
transformation making the matrix of the general equation of the ellipse
diagonal.
MA2ROTMAS is only on the CD.

244 5. MAXWELL’S THEORY
APPENDIX 5.3
A5.3.1 Phase Difference Between Internally Reflected
Components
We have mentioned above that elliptically polarized light may be produced by
total internal reflection. The incident light is reflected at a denser medium and
the two components, the p and s components, have a fixed phase angle between
them which is assumed to be zero. The reflected light is the superposition of
the two reflected components, each “picking up" a different phase angle upon
reflection. The difference between the two “new" phase angles after reflection is
the phase angle between the two components and may be calculated as
tan /2 (sin θ )
2
/[cos θ
((sin θ)
2
− (n
2
/n
1
)
2
)]. (A5.6)
We can get a graph of the angle from the complex reflection coefficients r
p
and r
s
. We just have to take the argument of r
p
/r
s
. This is done in FileFigA3.
FileFig A5.13 (MA3DIFINTRO)
A graph is shown of the difference between the arguments of the reflection
coefficients for internal total reflection.
MA3DIFINTRO is only on the CD.
Application A5.13. Observe the change of the difference angle depending on
the refractive index.
APPENDIX 5.4
A5.4.1 Jones Vectors and Jones Matrices
We have presented the two mutually perpendicular components propagating in
the X direction of the electrical field vectors. The phase angle φ between them
is
E
Y
jA exp i(k
1
X − ωt) (A5.7)
E
Z
kA exp i(k
1
X − ωt + φ). (A5.8)
One may want to write this in vector notation as
E
Y
E
Z
A exp i(k
1
X − ωt)
1
e
iφ
. (A5.9)

5.7. POLARIZED LIGHT 245
Disregarding the common factor A exp i(k
1
X−ωt) we may describe polarized
light by such vectors and have
1
0
horizontal
0
1
vertical (A5.10)
1/
√
2
1
0
+45 degrees 1/
√
2
0
1
-45 degrees (A5.11)
1/
√
2
1
−i
right circular 1/
√
2
0
i
left circular (A5.12)
All Jones vectors are listed in FileFig 5.14.
A5.4.2 Jones Matrices
We have discussed above the transformation between coordinate systems using
the rotation matrix and found, for example, that the rotation of 45
◦
degrees is
expressed as
EE
Y
E
Y
− E
Z
(A5.13)
EE
Z
E
Y
+ E
Z
. (A5.14)
In matrix formulation we have
EE
Y
EE
Z
1 −1
11
E
Y
E
Z
(A5.15)
In a similar martix representation we can obtain other operations on the two
components of the electrical field vectors (FileFig 5.14).
A5.4.3 Applications
We discuss two applications of the Jones vectors and Jones matrices.
Half-Wave Plate Between Crossed Polarizers
We start off with linear polarized light and apply the half-wave plate with 45
◦
orientation, disregarding the normalization factor. Then we do the multiplication
11
11
1
0
1
1
. (A5.16)
The result is 45
◦
polarized light. Then we apply the vertical linear polarizer and
obtain vertically polarized light.
00
01
1
1
0
1
. (A5.17)

246 5. MAXWELL’S THEORY
Quarter-Wave Plate Between Crossed Polarizers
We start off with linear polarized light and apply the quarter-wave plate as the
right circular polarizer, disregarding the normalization factor.
1 i
−i 1
1
0
1
−i
. (A5.18)
The result is circular polarized light. Then we apply the vertical polarizer
00
01
1
−i
0
−i
(A5.19)
and obtain right circular polarized light, passing the vertical polarizer.
FileFig A5.14 (MA4JONES)
Vector formulation of Jonesvectors for linear and circularpolarized light. Matrix
formulation of Jones matrices for linear polarizer, circular polarizer, and half-
wave and quarter-wave plates.
MA4JONES is only on the CD.
Application A5.14.
1. Derive Jones vectors for linear (−45
◦
), left circular, and right circular
polarized light.
2. Derive Jones matrices for the half-wave and quarter-wave plates.
3. Apply Jones matrices to Jones vectors for:
a. Matrices of horizontal and vertical polarizers, and the half-wave plate to
each horizontal, vertical, and 45
◦
Jones vector. Comment on the results.
b. Let light first be polarized horizontally, then pass a 45
◦
polarizer, and a
−45
◦
polarizer. Comment on the results.
c. What is the resulting matrix of a quarter-wave plate and then a half-wave
plate? What is the resulting operation?
d. What is the resulting matrix of a half-wave plate and then a quarter-wave
plate? What is the resulting operation?
e. What is the resulting matrix of a half-wave plate, then a quarter-wave
plate, and then another half-wave plate? What is the resulting operation?
See also on the CD
PM1. Time Averages (see p. 208).
PM2. Fresnel’s Formulas with the second Medium of higher Refractive Index
(see p. 214).
5.7. POLARIZED LIGHT 247
PM3. Fresnel’s Formulas with the second Medium of lower Refractive Index
(see p. 217).
PM4. Phase Angle Calculation for Total Reflection (see p. 217 and 242).
PM5. Transmission through two Interfaces (see p. 218).
PM6. Law of Refraction (see p. 220).
PM7. Reflection and Transmission Coefficients and Intensities (see p. 222).
PM8. Attenuation (at Total Reflection) in the less dense medium (see p. 22.)
PM9. Half Wave Plate, Quarter Wave Plate (see p. 231).
PM10. Quarter Wave Plate (see p. 235).
PM11. Elliptically polarized Light (see p. 23.)
PM12. Elliptically polarized Ligh (see p. 239).
