Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple
Подождите немного. Документ загружается.


6
6
CHAPTER
Maxwell II.
Modes and Mode
Propagation
6.1 INTRODUCTION
In the chapter on interference we discussed the resonance mode of a Fabry–
Perot. We found that all light was transmitted for a specific wavelength λ and
separation D of the Fabry–Perot plates. The condition for generation of the modes
was D mλ/2, where m was an integer.
The modes may be considered as a standing wave. A standing wave can be
described by the superposition of two traveling waves moving in opposite di-
rections. The standing waves are characterized by m + 1 nonmoving nodes,
including both nodes on the Fabry–Perot plates. Between the nodes, the ampli-
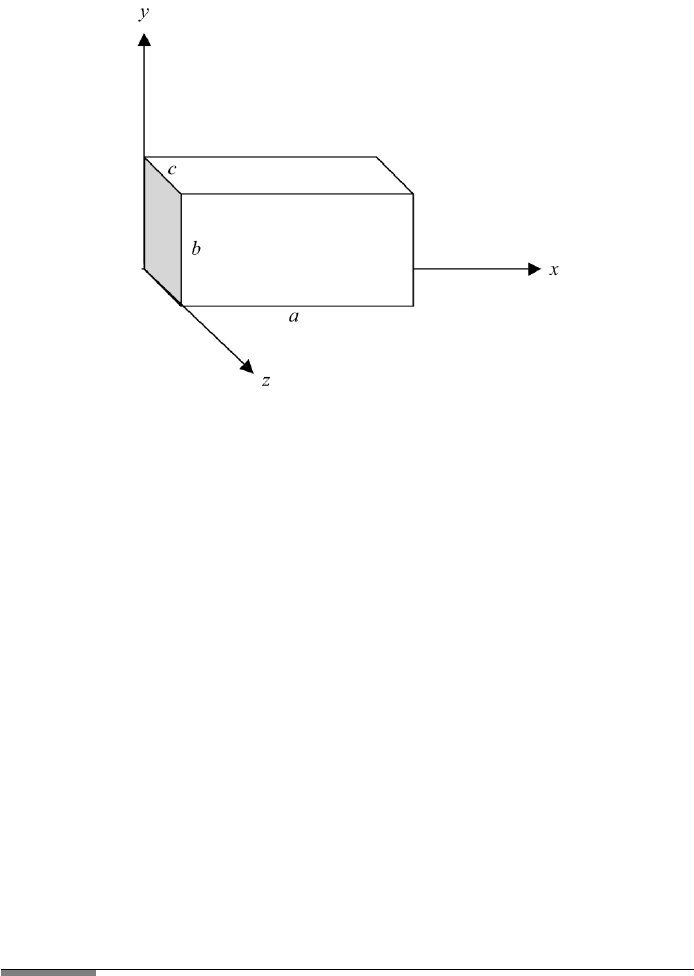
tudes oscillate from maximum to minimum. A rectangular box of dimensions a,
b, c with reflecting walls (Figure 6.1) has three pairs of parallel plates in the x,
y, and z directions. Each pair may be considered as a Fabry–Perot. The walls
are assumed to be perfectly reflecting, and the boundary conditions for the mode
formation are required to have nodes at the walls. Using plane wave solutions,
the modes are represented by sine functions. For the x direction, we have at
length a of the box that sin(2πa/λ
x
) 0or2πa/λ
x
π. A similar result is
found for the y and z directions and we have three standing wave conditions
a n
1
λ
x
/2,b n
2
λ
y
/2,c n
3
λ
z
/2. (6.1)
Since the n
i
s are integers, and a, b, c are constants, the possible values of the
wavelengths are restricted. Using wave vectors, Eqs. (6.1) may be written as
k
x
πn
1
/a k
y
πn
2
/b k
z
πn
3
/c. (6.2)
These are the wave vectors for the three components of a general mode of the
box. The corresponding wave vector is obtained by vector addition of the three
249
250 6. MAXWELL II. MODES AND MODE PROPAGATION
FIGURE 6.1 Coordinates for the discussion of the modes of a box with reflecting walls and
dimensions a, b, c.
components of Eq. (6.2). For the square of the scalar value one gets
k
2
π
2
{(n
1
/a)
2
+ (n
2
/b)
2
+ (n
3
/c)
2
}. (6.3)
The corresponding wave is a product of three standing waves in the three direc-
tions x, y, and z. The standing waves have fixed nodes, and the number of nodes
is related to the values of n
i
as (1 +n
i
) for i 1, 2, 3. Therefore, the number of
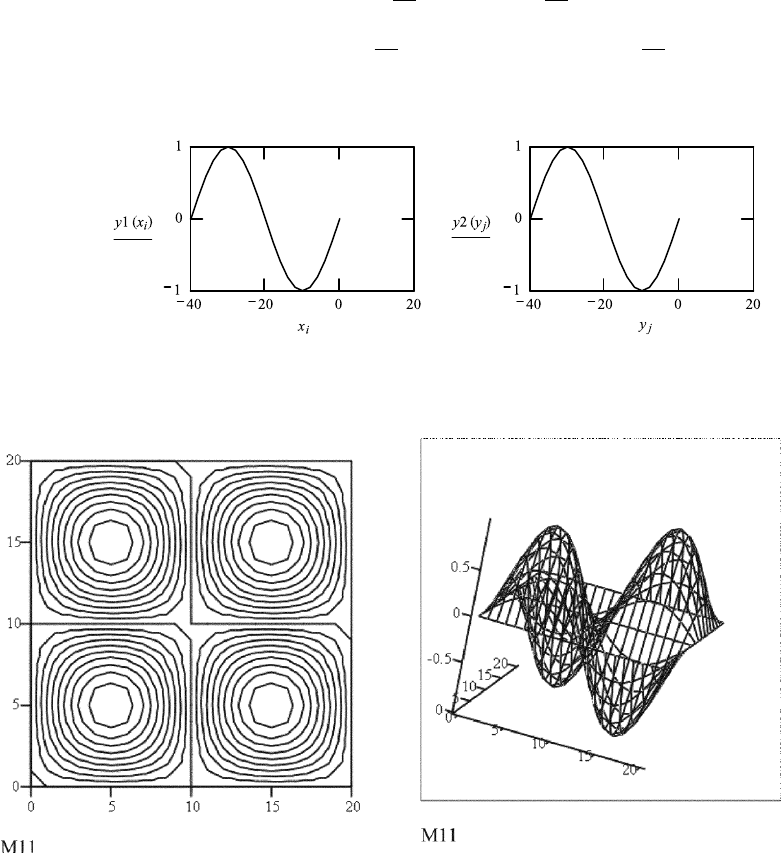
nodes may be used for the characterization of the modes. In FileFig 6.1 the first
two graphs show the one-dimension standing waves for the x and y directions
for the case of n
x
2 and n
y
2. The third and fourth graphs are the contour,
and surface plots of the amplitude for M
i,k
with i 2 and k 2 and the fifth
and sixth graph, show the intensity. In the third through sixth graphs we see six
node lines.
FileFig 6.1 (N1RECBOX)
Graphs of sine functions in one and two dimensions with nodes depending on
the integers n
1
, n
2
. The modes are numbered by Mik, where i gives the number
of nodes in the x direction and k in the y direction. Note that the node lines are
the same for the graphs of amplitude and intensity.
6.1. INTRODUCTION 251
N1RECBOX
Modes of the Rectangular Box in Two Dimensions
Standing sine waves in x and y directions. Mode number constants. x direction
n1 and a; y direction n2 and b. The wave in each direction is shown as well as
contour and surface plots. The square is also shown as surface plot.
i : 0 ...N j : 0 ...N
x
i
: (−40) + 2.001 · iy
j
: (−40) + 2.0001 · j
λ1: 2 ·
a
n1
λ2: 2 ·
b
n2
y1(x): sin
2 ·π ·
x
λ1
y2(y): sin
2 ·π ·
y
λ2
.
1. One dimension
2. Amplitude, 2 D
M11
i,j
: y1(x
i
) · y2(y
j
) n1 ≡ 2 a ≡ 40 n2 ≡ 2 b ≡ 40 N ≡ 20.
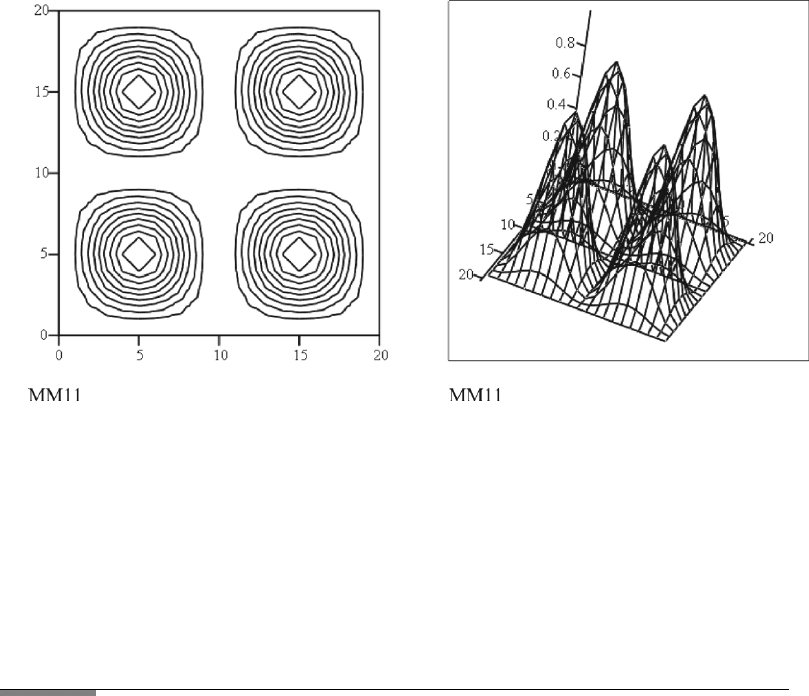
252 6. MAXWELL II. MODES AND MODE PROPAGATION
3. Intensity, 2D
MM11
i,j
: (y1(x
i
) · y2(y
j
))
2
.
Application 6.1.
1. Print out M00, M01, M10, M11, and M22.
2. Make graphs of M00, M01, M10, and M11, using a cosine function for x. The
corresponding boundary condition would be an “open end" of the box.
3. Make graphs of M00, M01, M10, and M11, using cosine functions for x and
y.
6.2 STRATIFIED MEDIA
In the chapter on geometrical optics we discussed image formation with spherical
mirrors. We also discussed astronomical telescopes composed of an objective
lens and magnifiers. Lenses always reflect some of the incident light, according
to Fresnel’s formulas. To reduce the reflection, an antireflection coating was
developed. A thin film of a specific material was vacuum-deposited on the lens
surface, preventing most of the incident light of a specific wavelength from being
reflected. In the same chapter we also discussed laser cavities. The mirrors of a
laser cavity need to have high reflectivity only for a limited wavelength range,
but the reflectivity should be close to one in order to obtain a high gain.
In this section we show that stacks of dielectric layers may have very high
reflectance or transmittance. Applications are antireflection coatings of lenses
and mirrors for laser cavities with extremely high reflectivity. We study the
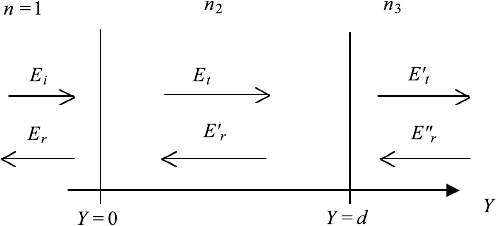
6.2. STRATIFIED MEDIA 253
FIGURE 6.2 Three media of index of refraction n
1
1, n
2
, and n
3
. In each medium we consider
a forward and a backward traveling wave.
reflection and transmission of light incident on stacks of dielectric layers. All
layers have the thickness d (1/4)(λ/n) n/4λ, but some may have different
refractive indices from others.
6.2.1 Two Interfaces at Distance d
When calculating Fresnel’s formulas, we equated the fields on both sides of
a boundary and obtained a set of linear equations for the amplitudes of the
reflection and the transmission coefficients. This method is called the boundary
value method and is now applied to two interfaces at distance d. In the chapter
on interference we studied the plane parallel plate and summed up all reflected
and transmitted waves. This method is called the summation method and is less
rigorous than the boundary value method. We consider three media and assume
normal incident light. In each medium we assume forward and backward trav-
eling waves (Figure 6.2). We do not show the time dependence of the waves,
giving us these equations for incident, reflected, and transmitted waves at the
two interfaces:
1. before the first interface
E
i
A
1
exp ik
1
(+Y ) incident (6.4)
E
r
A
1
exp ik
1
(−Y ) reflected, (6.5)
2. after the first interface
E
t
A
2
exp ik
2
(+Y ) transmitted after 1 (6.6)
E
r
A
2
exp ik
2
(−Y ) reflected back to 1, (6.7)
3. after the second interface
E
t
A
3
exp ik
3
(+Y ) transmitted after 2 (6.8)
E
r
A
3
exp ik
3
(−Y ) reflected back to 2. (6.9)
We take the electrical field vector perpendicular to the plane of incidence,
which is the case of perpendicular polarization discussed in Chapter 5. We first
254 6. MAXWELL II. MODES AND MODE PROPAGATION
take into account the electrical field vectors at boundary 1, where Y 0. The
sum of Eqs. (6.4) and (6.5) is equal to the sum of Eqs. (6.6) and (6.7). At the
boundary for Y d the sum of Eqs. (6.6) and (6.7) is equal to the sum of
Eqs. (6.8) and (6.9). We obtain the following equations
A
1
+ A
1
A
2
+ A
2
(6.10)
A
2
e
ikd
+ A
2
e
−ikd
A
3
e
ik
d
+ A
3
e
−ik
d
, (6.11)
where k 2πn
2
/λ, k
2πn
3
/λ, and d is the distance between the two
interfaces. In a similar manner we obtain a second set of two equations for the
B-fields. This is similar to the calculations of Fresnel’s formulas in Chapter 5,
applying the corresponding boundary conditions for the B-field at Y 0 and
Y d.
−A
1
+ A
1
−n
2
A
2
+ n
2
A
2
(6.12)
−n
2
A
2
e
ikd
+ n
2
A
2
e
−ikd
−n
3
A
3
e
ik
d
+ n
3
A
3
e
−ik
d
. (6.13)
In order to derive a vector-matrix formulation, we abbreviate the sum of the
amplitudes before the first boundary (Eq. (6.10)), by E
1,d0
. Since Eq. (6.11)
was derived using the magnetic field vector we call the amplitude B
1,d0
.Ina
similar way we use E
2,d0
and B
2,d0
for the sum of the amplitudes after the
first boundary. For the amplitudes before and after the second boundary, we use
E
2,dd
and B
2,dd
, and E
3,dd
and B
3,dd
, respectively. We may now write
E
1,d0
A
1
+ A
1
A
2
+ A
2
E
2,d0
(6.14)
B
1,d0
−A
1
+ A
1
−n
2
A
2
+ n
2
A
2
B
2,d0
(6.15)
E
2,dd
A
2
e
ikd
+ A
2
e
−ikd
A
3
e
ik
d
+ A
3
e
−ik
d
E
3,dd
(6.16)
B
2,dd
−n
2
A
2
e
ikd
+ n
2
A
2
e
−ikd
−n
3
A
3
e
ik
d
+ n
3
A
3
e
−ik
d
B
3,dd
. (6.17)
Equations (6.14) and (6.15) may be written in matrix notation as
Field
1,d0
E
1,d0
B
1,d0
11
−11
A
1
A
1
M
1,0
A
1
(6.14) and (6.15)
Field
2,d0
E
2,d0
B
2,d0
11
−n
2
+n
2
A
2
A
2
M
2,0
A
2
(6.14) and (6.15)
and have
M
2,0
A
2
M
1,0
A
1
or
A
2
M
−1
2,0
M
1,0
A
1
M
−1
2,0
Field
1,d0
. (6.18)
Equations (6.16) and (6.17) may be written in matrix notation as
Field
2,dd
e
ikd
e
−ikd
−n
2
e
ikd
+n
2
e
−ikd
A
2
A
2
M
2,d
A
2
(6.16) and (6.17)

6.2. STRATIFIED MEDIA 255
Field
3,dd
e
ik
d
e
−ik
d
−n
3
e
ik
d
n
3
e
−ik
d
A
3
A
3
M
3,d
A
3
(6.16) and (6.17)
and we have
Field
3,dd
M
3,d
A
3
M
2,d
A
2
. (6.19)
We want to express the vector Field
3,dd
as the product of matrices times the
vector Field
1,d0
, and have
Field
3,dd
M
2,d
A
2
M
2,d
M
−1
2,0
Field
1,d0
. (6.20)
The manipulation of the matrices is shown in FileFig 6.2.
FileFig 6.2 (N2SYMATR)
Demonstration of the matrix manipulations and multiplication of M
2,d
M
−1
2,0
and
the resulting matrix M
2
.
M
2
cos(kd) −i sin(kd)/n
2
−n
2
i sin(kd) cos(kd)
. (6.21)
N2SYMATR is only on the CD.
The final result is
E
3,dd
B
3,dd
cos(kd) −i sin(kd)/n
2
−n
2
i sin(kd) cos(kd)
E
1,d0
B
1,d0
. (6.22)
Using this matrix approach, we discuss some applications.
6.2.2 Plate of Thickness d (λ/2n
2
)
We apply Eq. (6.22) to a plate of thickness d (λ/2n
2
)q, where q is an integer.
The thickness of the plate is a multiple of half a wavelength divided by the
refractive index n
2
of the material of the plate. Using k 2πn
2
/λ and d
(λ/2n
2
)q we have for the product kd qπ. At the boundary we have for the
exponentials e
−ik
d
e
−ikd
. Both are 1 for even q. Equation (6.22) is now
E
3,dd
B
3,dd
10
01
E
1,d0
B
1,d0
. (6.23)
The matrix M is the unit matrix and the result is that the medium of thickness
d has no effect on the transmitted fields. The same result is obtained when q is
odd. A similar result has been obtained in Chapter 2 for the plane parallel plate.
All incident power of the particular wavelength λ will be transmitted when the
plate has the thickness d (λ/2n
2
)q.
256 6. MAXWELL II. MODES AND MODE PROPAGATION
6.2.3 Plate of Thickness d and Index n
2
We apply Eq. (6.22) to a plate of thickness d with refractive index n
2
. We also
assume that there is no backwards traveling wave in medium 3 and that the
refractive indices of the first and third media are assumed to be 1. We then have
A
3
e
ik
d
−A
3
e
ik
d
cos(kd) −i sin(kd)/n
2
−n
2
i sin(kd) cos(kd)
A
1
+ A
1
−A
1
+ A
1
. (6.24)
In FileFig 6.3 we calculate the transmitted intensity of a plane parallel plate.
Calling x A
1
/A
1
and y A
3
/A
1
and observing that e
ik
d
1, we have
R xx
∗
for the reflected intensity and T yy
∗
for the transmitted intensity.
Equation (6.24) is a system of two linear equations in x and y and is solved for
x and y. The result for T is
T 1/[1 +{(n
2
− 1)
2
/4n
2
}(sin(kd)
2
]. (6.25)
Here we can use T for the transmitted intensity because we have assumed that
the refractive index in the first medium is n
1
1. This is the same result one
obtains with the summation method for the case of normal incidence, discussed
in Chapter 2.
FileFig 6.3 (N3SYMATPL)
Calculation of the transmitted intenstiy T of a plane parallel plate of thickness
d with indices outside the plate equal to 1. We use x A
1
/A
1
and y A
3
/A
1
and have T yy
∗
for the transmitted intensity and R xx
∗
for the reflected
intensity.
N3SYMATPL is only on the CD.
Application 6.3.
1. Calculate the reflected intensity R.
2. Make graphs for T and R in the wavelength range from 1 to 20 microns. Use
for d values equal to kd qπ, one for q even and one for q odd.
3. Make graphs for T for two different refractive indices between 1.1 and 4 in
the wavelength range from 1 to 20 microns. Use for the thickness d values
not equal to kd qπ, q even or odd.
6.2.4 Antireflection Coating
Antireflection coating may be found on camera lenses. A thin dielectric film
of refractive index n
2
is vacuum-deposited on the surface of a lens of refractive
index n
3
. We assume for the film a thickness λ/(4n
2
). The light is incident from a

6.2. STRATIFIED MEDIA 257
medium with index n
1
and the product kd in Eq. (6.22) is [(2πn
2
/λ)(λ/4n
2
)]
π/2. One gets
A
3
e
ik
d
−n
3
A
3
e
ik
d
0 −i/n
2
−n
2
i 0
A
1
+ A
1
−n
1
A
1
+ n
1
A
1
. (6.26)
Because e
ik
d
i one has
iA
3
(−i/n
2
)(−n
1
A
1
+ n
1
A
1
) (6.27)
−n
3
iA
3
(−in
2
)(A
1
+ A
1
). (6.28)
To get to the condition for no reflection, we set the ratio A
1
/A
1
0 and have
A
3
/A
1
n
1
/n
2
n
2
/n
3
(6.29)
or
n
1
n
3
n
2
2
. (6.30)
We have the result: the antireflection film of a thickness of a quarter-wavelength
must have a refractive index equal to the square root of the product of the re-
fractive index on both sides. Let us consider a glass lens of index n
3
1.5. The
incident light travels in the medium with n
1
1 and n
3
1.5 being the index
of the lens. The square root of the product is 1.22. A material with exactly that
refractive index is hard to find, but material with approximately that value is used
for antireflection coating.
In FileFig 6.4 we calculate from Eqs. (6.27) and (6.28) the reflection coefficient
r A
1
/A
1
and the transmission coefficient t A
3
/A
1
and investigate the
reflected and transmitted intensities. Using rr
∗
R and tt
∗
, the sum R +tt
∗
is
not 1. However, if we use the correct expression for T (see Chapter 5), we show
that (n
3
/n
1
)tt
∗
is equal to T and that one has R + T 1. The graph in FileFig
6.4 shows a plot of the antireflection coating depending on the refractive index
n
2
.
FileFig 6.4a (N4SYMULANTa)
Antireflection coating. The reflected amplitude r A
1
/A
1
and the transmitted
amplitude t A
3
/A
1
as solutions of Eq. (6.26). The products rr
∗
and tt
∗
are
also calculated.
FileFig 6.4b (N4SYMULANTb)
Numerical calculations.

258 6. MAXWELL II. MODES AND MODE PROPAGATION
1. Special case of zero thickness for demonstration of reflected and transmitted
intensities.
2. Antireflection coating.Graph of reflected intensity depending on the refractive
index of the coating.
N4SYMULANTa and N4SYMULANTb are only on the CD.
Application 6.5.
1. Using the correct expression for T (see chapter 5), derive formulas for the
transmitted and reflected intensities for one interface with refractive indices
n1 and n2 1. Show that T + R 1.
2. Find the refractive index for an antireflection coating material for silicon
(n 3.4).
3. Use polyethylene (n 1.5) as a coating of silicon and calculate the
percentage of reflected amplitude and intensity.
6.2.5 Multiple Layer Filters with Alternating High and Low
Refractive Index
High-reflecting dielectric mirrors are composed of a large number of dielectric
layers with alternating high and low refractive indices. We extend Eq. (6.22) to
f − 1 layers of equal thickness and obtain
E
f,dd
B
f,dd
M
f −1
M
f −2
,...,
E
1,d0
B
1,d0
. (6.31)
For a rigorous derivation see Born and Wolf (1964; p.66).
We apply Eq. (6.31) to a sequence of double layers, consisting of a high and
a low refractive index, assuming that the refractive index outside is 1. Assuming
N double layers the sequence of the refractive indices is then
(n 1)(n
H
n
L
),...,(n
H
n
L
)(n 1). (6.32)
The product of the matrices is
(M
H
M
L
),...,(M
H
M
L
). (6.33)
The thickness of one layer is assumed to be one-quarter of a wavelength and
we have the product kd [(2πn
2
/λ)(λ/4n
2
)], resulting in sin(kd) 1 and
cos(kd) 0. For one double layer we get for the product of M
H
times M
L
−n
L
/n
H
0
0 −n
H
/n
L
(6.34)
and for N double layers
(−n
L
/n
H
)
N
0
0(−n
H
/n
L
)
N
. (6.35)
