Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple

Подождите немного. Документ загружается.

188 4. COHERENCE

C1COH2S

Intensity of Two Sources Separated by s

Superposition of two double slit patterns. The slits have width d and separation

a; one pattern is untilted with ψ  0, the other tilted by ψ  x/Z, and distance

from sources to slit is Z. Distance from slit to screen is X, coordinate on screen

is Y , Y/X  θ. By enlarging ψ, starting from 0, one ﬁnds the ﬁrst fringe

disappearance. If ψ is further enlarged, the fringes reappear, but now the minima

are not zero. Another point of view: fringes may disappear for constant s and

changing a.

θ ≡−.006, −.00599.. .006 d ≡ .05 a : 1 Z ≡ 9000 λ : .0005

I 1(θ ):

sin



(π) ·

· sin(θ )



π ·

· (sin(θ ))

· cos



π ·

· (sin(θ ))

II1(θ):

sin



π ·

· (sin(θ ))



π ·

· (sin(θ ))

· cos



π ·

· (sin(θ ) +sin(ψ1))

s1 ≡ 0

ψ1 ≡

II2(θ):

sin



π ·

· (sin(θ ))



π ·

· (sin(θ ))

· cos



π ·

· (sin(θ ) +sin(ψ2))

s2 ≡ 1.5

ψ2:

II3(θ):

sin



π ·

· (sin(θ ))



π ·

· (sin(θ ))

· cos



π ·

· (sin(θ ) +sin(ψ3))

s3 ≡ 2.25

ψ3:

4.1. SPATIAL COHERENCE 189

II4(θ):

sin



π ·

· (sin(θ ))



π ·

· (sin(θ ))

· cos



π ·

· (sin(θ ) +sin(ψ4))

s4 ≡ 2.6

ψ4:

Application 4.1.

1. Change d to 0.1 and determine the s value for disappearance of fringes. Save

the changed values for future comparisons.

2. Change λ to 0.0006 and determine the s value for disappearance of fringes.

Save the changed values for future comparisons.

3. Change a to 1.2 and determine the s values for disappearance of fringes.

Save the changed values for future comparisons.

4.1.3 Coherence Condition

We have seen that the two source points produce superimposed intensity patterns

for certain distances s between them. In our case we found fringes for distance

s  0, and for a larger distance s  2.25mm, the fringes disappeared. For a

small separation s of the two source points, one would observe fringes similar to

the pattern produced by one source point. The coherence condition tells us how

large one can make the separation s and still have a fringe pattern similar to the

one produced by one source point only. For the discussion, we assume that the

openings of the two slits are very small and therefore we may omit diffraction.

190 4. COHERENCE

ψ λ

ψ ω

ω λ

FIGURE 4.2 The condition a sin ψ  a(s/Z)  λ/2 is equivalent to sa/Z  s sin ω  λ/2

and tells us that the product of the distance between the source times the opening angle must be

similar to that of a pointlike source.

We then have for the pattern generated by sources S

and S

(θ,0)  I

{cos[(πa/λ) sin θ]}

(4.3)

(θ,ψ)  I

{cos[(πa/λ)(sin θ − sin ψ)]}

. (4.4)

The center of the pattern of I

is at (a sin θ )  0 and the ﬁrst minimum is at

(a sin θ )  λ/2. We want to ﬁnd the magnitude of the angle ψ for which we will

see only one fringe pattern. If the center of the pattern of I

is at the minimum of

(i.e., for (a sin ψ )  λ/2), the angle ψ is too large and we are at the position

where fringes disappear for the ﬁrst time. Therefore, in order to observe just one

fringe pattern of the superposition of I

and I

we have to require that

(a sin ψ)  λ/2. (4.5)

Equation (4.5) may also be written in good approximation as s ·a/Z, where a/Z

is the opening angle ω from the source points (Figure 4.2) and one has

s ·a/Z  s · ω  λ/2. (4.6)

The opening angle ω seen from the middle of the two source points is given as

a/Z and the product of this angle times the separation s of the source points

must be small compared to half of the wavelength. We state this as

(source size) times (opening angle ω) must be  λ/2. (4.7)

This is called the coherence condition.

4.1.4 Extended Source

The discussion of the double star was the ﬁrst step in investigating the question

of how far away a source has to be to qualify as a point source, even if it has a

4.1. SPATIAL COHERENCE

191

ﬁnite diameter. To discuss an extended source we look at a line source made of a

sequence of point sources. The distance between the source points is considered

inﬁnitesimally small, but there is no ﬁxed phase relation between the light of one

source point with respect to any other. We apply to the line source what we have

done for two source points, and now have to integrate I (θ,ψ) over the angle ψ

from 0 to ψ

 s/Z





s/Z

{sin[(πd/λ)(sin θ − sin ψ)]/[(πd/λ)(sin θ −sin ψ)]}

·{cos[πa/λ)(sin θ − sin ψ)]}

dψ. (4.8)

The integration may be interpreted as the superposition of the intensity fringe

pattern, produced by all source points between S

and S

. The upper integration

limit, that is, the angle s/Z, is taken as such a numerical value that we can

compare the angles with calculations of the fringes for the two point sources.

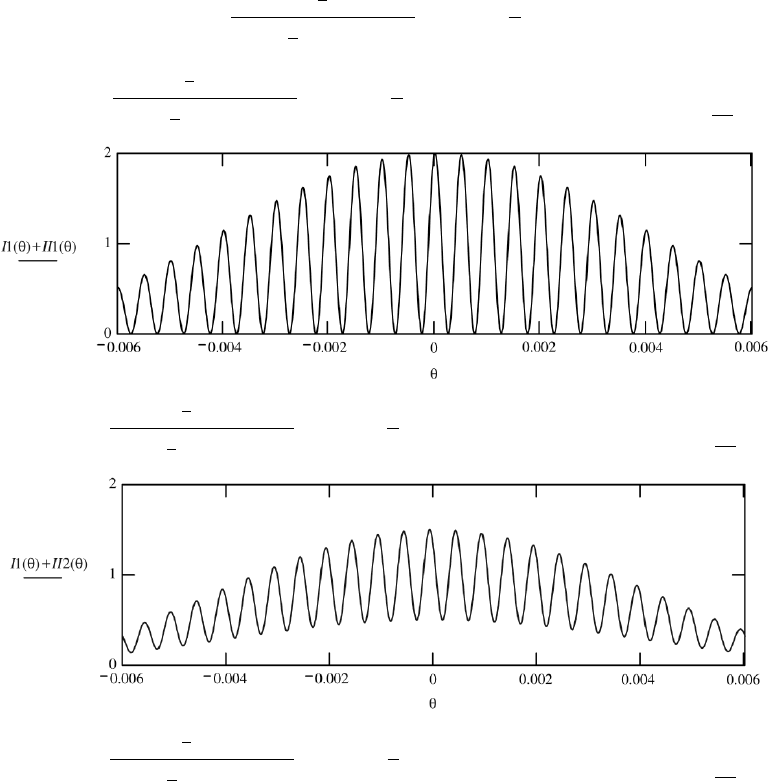
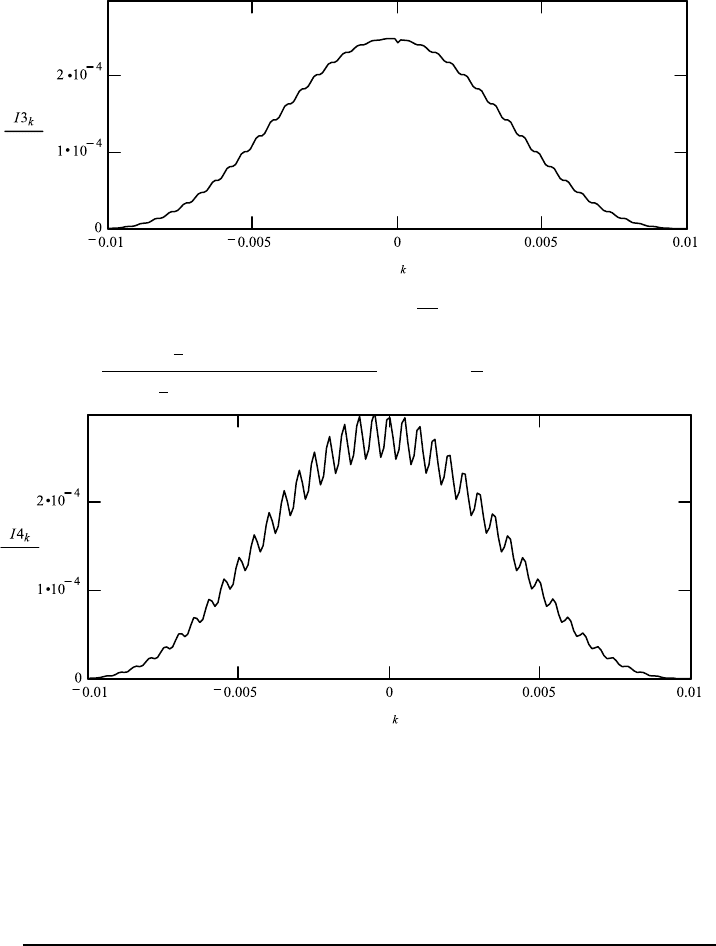
The ﬁrst graph in FileFig 4.2 shows the intensity interference pattern for a line

source of length s  1 mm. The second graph for the length of s  1.5mmagain

shows a fringe pattern. The third graph shows the disappearance of the intensity

pattern at a length of s  4.5, and the fourth graph shows the reappearance at

s  5. We see that the integrated intensity pattern is produced by an extended

source of length s  4.5 mm. All fringes cancel for s  4.5 mm. This value is

twice as large as s  2.25 mm, the value we found for the two source points.

We may associate the length of a line source with the diameter of a circular

source. The disappearance of the interference pattern occurs when the diameter

of the circular source is twice the distance of the two source points. In Figure 4.3

we show an experimental setup to observe a fringe pattern of an extended source.

The coherence condition (Eq. (4.7)) may be applied to the extended source

as well. One has that the area s times the solid angle a/Z of the source must

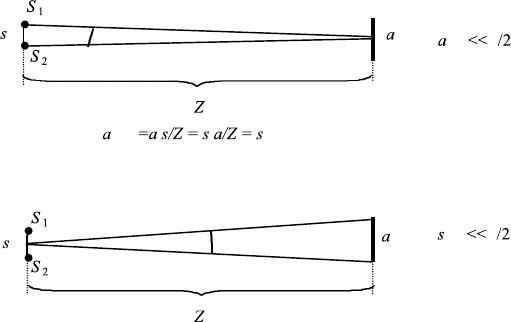
FIGURE 4.3 Laboratory setup for the observation of fringes from an extended source. Experi-

mental values: B  20 m, X  1 m, width of S

and S

 .4 mm, b  6 mm, λ  .00057 mm.

At 2a  2 mm, the fringes disappear for the ﬁrst time, and the upper limit of the experiment is

2a  4 mm. (Adapted from Einf¨uhrung in die Optic, R.W. Pohl, Springer-Verlag, Heidelberg,

1948.)

192 4. COHERENCE

be small compared to (1/2)λ. This condition must be obeyed when setting up

Young’s experiment. The source point is the illuminated hole of the ﬁrst screen

and must be so small and far away that the wave at the next two holes has a ﬁxed

phase relation. The size of the hole must be determined by the opening angle a/Z

of the experimental setup. On the other hand, a star may be very large, but if the

star is so far away that the product s times the opening angle ω (see Figure 4.2)

is small compared to λ/2, the coherence condition is met. As the result, the light

from the star is like parallel light when entering the double slit. Fringes may be

observed and the light of the “large star" is called spatially coherent.

FileFig 4.2 (C2COHEX)

Graphs are shown for the superposition of the integrated intensities I (θ,ψ

)

depending on the upper limit of the integration values ψ

of the angle ψ

 s/Z.

Four values of ψ

are used, correspondingto s  1mm, s  1.5 mm, s  4.5 mm,

and s  5 mm. Parameters used are the separation of the two openings a  1mm,

opening of the slits d  0.05 mm, wavelength λ  0.0005 mm, distance from

source to the double slit Z  9000mm, and distance fromaperture to observation

screen X  4000 mm. By choosing the same values for a and λ as used in

FileFig 4.1, we ﬁnd fringes disappear for the ﬁrst time for the size of the source

of s  4.5 mm, that is, twice as large as found for the distance between the

two point sources. Fringe patterns are observed for separations s smaller than

4.5 mm. For s  4.5 mm we have disappearance of fringes for the ﬁrst time. For

s larger than 4.5 mm the fringe pattern reappears.

C2COHEX

Intensity of an Extended Source

Width is s and interference diffraction is on a double slit. Slit openings are d and

separation a, distance from source to slit Z, from slit to screen X, coodinare on

screen is Y , and small angle approximation Y/X  θ.

a : 1 d ≡ .05

0 ≤ ψ ≤ 2 k ≡ 0..200 θ

≡ .01 − k ·.0001 λ : .0005 Z  9000

s1 ≡ 1 ψ

≡

I 1

:



sin



π ·

· (sin(θ

) + sin(ψ))



π ·

· (sin(θ

) + sin(ψ))

· cos



π ·

· (sin(θ

) + sin(ψ))

dψ.

4.1. SPATIAL COHERENCE 193

s2 ≡ 1.5 ψ

≡

I 2

:



sin



π ·

· (sin(θ

) + sin(ψ))



π ·

· (sin(θ

) + sin(ψ))

· cos



π ·

· (sin(θ

) + sin(ψ))

dψ.

s3 ≡ 4.5 ψ

≡

I 3

:



sin



π ·

· (sin(θ

) + sin(ψ))



π ·

· (sin(θ

) + sin(ψ))

· cos



π ·

· (sin(θ

) + sin(ψ))

dψ.

194 4. COHERENCE

s4 ≡ 5 ψ

≡

:



sin



π ·

· (sin(θ

) + sin(ψ))



π ·

· (sin(θ

) + sin(ψ))

· cos



π ·

· (sin(θ

) + sin(ψ))

dψ.

Application 4.2.

1. Change d to 0.1 and determine the s value for disappearance of fringes.

Compare to FileFig 4.1.

2. Change λ to 0.0006 and determine the s value for disappearance of fringes.

Compare to FileFig 4.1.

3. Change a to 1.2 and determine the s values for disappearance of fringes.

Compare to FileFig 4.1.

4.1.5 Visibility

4.1.5.1 Visibility for Two Point Sources

We have discussed appearance and disappearance of fringe patterns for two point

sources at variable distances, and for extended sources of variable diameters. To

4.1. SPATIAL COHERENCE 195

measure how well the fringes may be seen, Michelson has deﬁned the visibility

of fringes as the absolute value of

V 



tot,max

− I

tot,min

tot,max

+ I

tot,min



. (4.9)

The intensities are taken in the nominator and denominator of one fringe. For the

pattern shown in the ﬁrst graph of FileFig 4.2, one has I

max

 1 and I

min

 0

and obtains for the visibility, V  1. When considering the superposition of two

intensity patterns, one has to determine I

max

and I

min

depending on the angle

ψ. We saw that the angle ψ is small because Z is large and applied the small

angle approximation (i.e., sin θ  Y/X and sin ψ  Y



/X). From Eqs. (4.3)

and (4.4), disregarding the diffraction factors, we have for the total intensity I

tot

(i.e., the sum of Eqs. (4.3) and (4.4)),

tot

(Y ) {cos[(π a/λX)(Y )]}

+{cos[(πa/λX)(Y − Y



)]}

. (4.10)

Using 2 cos

α/2  1 + cos α,weget

tot

(Y )  1 + 1/2{cos[(2πa/λX)(Y )]}+1/2{cos[(2π a/λX)(Y − Y



)]}, (4.11)

and with cos α +cos β  2 cos{(α +β)/2}cos{(α − β)/2} one has

tot

(Y )  1 +{cos[(2πa/λX)(Y



/2)]}{cos[(2πa/λX)(Y − Y



/2)]}. (4.12)

The minimum and maximum values of I

tot

depend only on Y , since Y



is ﬁxed

by the angle ψ for which we want to determine the visibility. The maximum

value of {cos(2πa/λX)(Y − Y



/2)} is 1 because that is the maximum of the

cos-function and similarly the minimum value is −1. We have therefore

tot,max

 1 +{cos[(2πa/λX)(Y



/2)]}

tot,min

 1 −{cos[(2πa/λX)(Y



/2)]} (4.13)

and using the deﬁnition of Eq. (4.9) one obtains for the visibility

V |cos(π a/λX)(Y



)|. (4.14)

For small values of ψ  Y



/X  s/Z we have a maximum. The ﬁrst zero of

the visibility is for πaY



/λX  π/2; that is, Y



/X  s/Z  λ/2a.

In FileFig 4.3 we have plotted Eq. (4.14), using similar values to those in

FileFig 4.1. We observe that the visibility is ﬁrst zero for s  2.25 mm, the value

we determined in FileFig 4.1 for the ﬁrst disappearance of the fringes. For larger

values of s we found reappearance of fringes (see the fourth graph of FileFig

4.1).

The interval from s  0 to the value of s for which the visibility is ﬁrst zero

is called the coherence interval.

196 4. COHERENCE

FileFig 4.3 (C3VIS2S)

Graph of the visibility for two point sources.

C3VIS2S is only on the CD.

Application 4.3.

1. Change λ to 0.0006 and determine the s value for V  0. Compare to FileFig

4.1.

2. Change a to 1.2 and determine the s value for V  0. Compare to FileFig

4.1.

4.1.5.2 Visibility for an Extended Source (Line Source)

The visibility for an extended source is obtained by determination of I

tot,max

and

tot,min

of the total integrated intensity. Again, disregarding the diffraction factor,

one has

tot

(Y )  I



s/Z

{cos[(πa/λ)(sin θ − sin ψ)]}

dψ. (4.15)

We calculate in small angle approximation the integral

tot

(Y )  I



{cos[(πa/λ)(Y/X − Y



/X)]}

d(Y



/X). (4.16)

First one has to go through the steps of Eqs. (4.10) to (4.12) and determine the

maxima and minima. The second step is the integration of Eq. (4.14) and the

result is

V |{sin(π a/λX)(Y



)}/(πa/λX)(Y



)|, (4.17)

where Y



/X  s/Z. The ﬁrst minimum of the visibility is obtained at

(πa/λX)Y



 π, (that is for Y



/X  λ/a). This is twice the value we found for

the two point sources at distance s. In FileFig 4.4 we have plotted, for similar

values to those used in FileFig 4.2, Eq. (4.17) as a function of the length s of the

extended source. One ﬁnds the ﬁrst disappearance of the fringes at s  4.5, the

same value determined in FileFig 4.2.

FileFig 4.4 (C4VISEX)

Graph of the visibility for an extended source.

C4VISEX is only on the CD.

4.1. SPATIAL COHERENCE 197

Application 4.4.

1. Change λ to 0.0006 and determine the s value for V  0. Compare to FileFig

4.2.

2. Change a to 1.2 and determine the s value for V  0. Compare to FileFig

4.2.

4.1.6 Michelson Stellar Interferometer

In the discussion of the intensity pattern produced byYoung’s experiment for the

two source points and the extended source, we assumed a ﬁxed separation a of

the two openings. We studied the change in the intensity pattern depending on

the separation s of the source points and the diameter s of the extended source.

Michelson was interested in the measurement of the diameter of a star. In the

Young’s experiment we discussed above, the separation a of the two slits was

ﬁxed and the distance between the two source points s was varied. Application

of this experiment to the measurement of the diameter of a star is very difﬁcult

because both parameters s and a are ﬁxed. Michelson wanted to modifyYoung’s

experiment by making the separation a variable. However, since the diameter

he wanted to measure was so small, the setup of Young’s experiment had to be

modiﬁed.

We start with Young’s experiment for two source points. The fringe pattern of

the superposition of the two patterns on the observation screen depends on the

distance of the two source points. This is shown in Fig. 4.4a. The intensities of

the two source points are for small angles

 A

{cos(πaθ/λ)}

(4.18)

 A

{cos(πa(θ − φ)/λ)}

. (4.19)

The angle φ is what we wish to determine. In the setup of Figure 4.4a the

displacement of the intensity pattern of source I with respect to source II is

limited by the size of the distance a between the two slits. The modiﬁcation is

shown in Figure 4.4b. A new parameter h of the large distance between the ﬁrst

two mirrors is introduced. Changing the length h produces a change of the fringe

pattern. From the variation of the fringes for two values of h one can determine

the angle φ. In Figure 4.4b we show the modiﬁed setup and the two intensity

patterns are now given as

 A

{cos(πaθ/λ)}

(4.20)

 A

{cos[π(aθ −hφ)/λ]}

. (4.21)

The superposition u

+ u

will show maxima and minima depending on h for

ﬁxed φ and a. We may calculate the angle φ from the observed h values for a

resulting maximum and the following minimum. For a resulting maximum we