Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple

Подождите немного. Документ загружается.

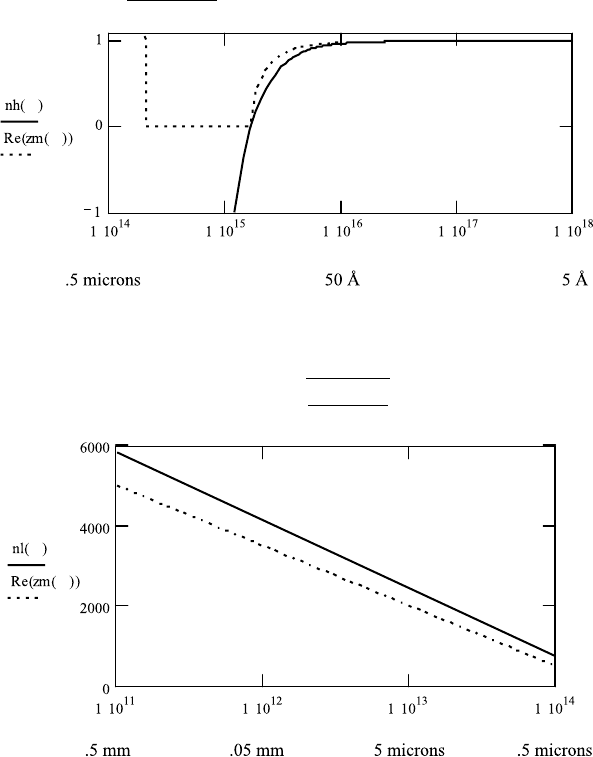
330 8. OPTICAL CONSTANTS

2. High frequency limit

nh(ω): 1 −

εo · ω

· τ

. . . . .

3. Low frequency limit

nl(ω):

2 ·εo · ω

. . . .

frequency

3 ·10

is1mm

3 ·10

is 1 micron

3 ·10

is1mm is10

frequency

1 ·10

is3mm

1 ·10

is 3 micron

1 ·10

is3mm is30

angular frequency

1 ·10

is 3/(2 ·π )mm

1 ·10

is 0.477 micron

1 ·10

is 0.477 mm is 40

Application 8.5.

1. Check your computer program manual and get familiar with physical unit

systems, MKS, and cgs.

2. Modify the calculations for gold, 4.5 · 10

[1/Ohm m].

3. Modify the calculations for silver, 6.3 · 10

[1/Ohm m].

8.4. OPTICAL CONSTANTS OF METALS 331

4. Modify the calculations for nickel, 1.5 · 10

[1/Ohm m].

5. Modify the calculations for lead, 0.5 · 10

[1/Ohm m].

6. Compare the graphs for the long wavelength region. At what frequency have

the absolute values of n and K about the same value? At what frequency have

the optical constants of all metals about the same value?

8.4.4 Skin Depth

In the low frequency region, where the light is strongly attenuated in the metal,

the light may only penetrate into the metal a small distance, called the skin depth.

An incident wave u

exp −i(ωt + kX) may be written with complex k

∗

u  u

exp −iωt exp −i{(n − iK)ωX/c}. (8.59)

We write Eq. (8.58) in real and complex factors as

u  u

exp −(ωKX/c)exp−iω{t − nX/c}. (8.60)

One deﬁnes the penetration depth as the length at which the wave is attenuated

to 1/e, that is,

 l  c/ωK 



[(2c

)/(ωσ)]. (8.61)

In most cases one is interested in the intensity and has



/2ωσ ] (8.62)

or with a good conductor such as copper, with σ  5.76 10

(ohm meter)

−1

one

gets with ω in sec

−1

 .17{



[(1sec

−1

/ω)]} meter . (8.63)

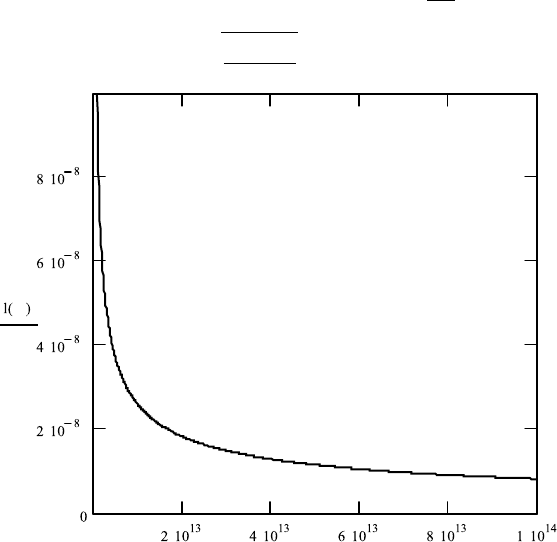
In FileFig 8.6 the ﬁrst graph shows the penetration depth for the intensity

of frequencies in the range of 10

, the visible and near infrared. The second

graph shows the penetration depth for the intensity of frequencies in the long

wavelength range.

FileFig 8.6 (O6SKINS)

Graph of the skin depth of the intensity for copper in the wavelength range from

−3

to 10

−7

332 8. OPTICAL CONSTANTS

O6SKINS

Skin Depth

1. Skin depth (in meters) for intensity depending on frequency

εo : 8.85 · 10

−12

/Nm c : 3 ·10

m/s

σ : 6 · 10

(Am)

−1

ω : 10

, (10)

...10

i :

√

−1

l(ω)



εo · c

2 ·ω · σ

in meters.

. . . . .

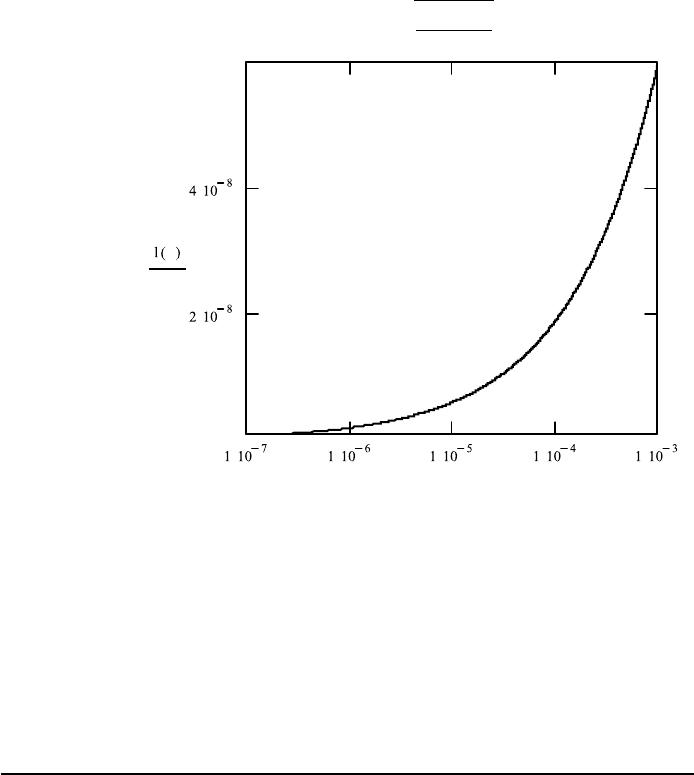
8.4. OPTICAL CONSTANTS OF METALS 333

2. Skin depth (in meters) for intensity depending on wavelength

(For checking: for 1 mm wavelength angular frequency is 2π ·3 · 10



l(λ):

εo · c · λ

4π · σ

. . . . .

1 · 10

meter is 1 nm  .001 microns  10

Application 8.6.

1. Derive the penetration depth for the intensity, Eq. (8.61).

2. Check your Mathcad manually and get familiar with physical unit systems,

MKS, and cgs.

3. Modify the calculations for gold, 4.5 · 10

[1/Ohm m].

4. Modify the calculations for silver, 6.3 · 10

[1/Ohm m].

5. Modify the calculations for nickel, 1.5 · 10

[1/Ohm m].

6. Modify the calculations for lead, 0.5 · 10

[1/Ohm m].

8.4.5 Reﬂectance at Normal Incidence and Reﬂection

Coefﬁcients with Absorption

We have seen in Section 8.3 that the r



component is not zero at the principal

angle, which means the angle corresponding to the Brewster’s angle for the case

of the lossless dielectric. The reﬂectance R is equal to the square of the reﬂection

coefﬁcients of Fresnel’s formulas, (Eq. (8.32) and (8.33)) and is valid for both

dielectric and metals if the corresponding values of n and K are used. For normal

incidence, when the parallel and perpendicular components are the same we have

334 8. OPTICAL CONSTANTS

for the reﬂectance R,

R  (1 −n)

+ K

/[(1 + n)

+ K

]. (8.64)

In FileFig 8.7 we show for normal incidence the dependence of the reﬂectance

R on K. When K  0 we go back to Fresnels formulas, depending only on the

real part of the refractive index, as discussed in Chapter 5 for lossless dielectrics.

When K is large, we have high reﬂectance R as observed for metals.

FileFig 8.7 (O7REFNKS)

Graph of the reﬂectance at normal incidence depending on K.

O7REFNKS is only on the CD.

8.4.6 Elliptically Polarized Light

We mentioned in Chapter 5 that elliptically polarized light may be produced

when light is totally internally reﬂected in a dielectric medium. Reﬂection on

metal surfaces shows a similar phenomenon. The reﬂection coefﬁcients r

and r

may have arguments depending on the angle of incidence. Since each component

picks up a different change in the argument, the difference of the arguments of

the reﬂected components is not the same and corresponds to the angle φ of

elliptically polarized light, as discussed in Chapter 5.

In FileFig 8.8 we have plotted the difference of the phase angles after

reﬂection, depending on the angle of incidence.

FileFig 8.8 (O8ARDELS)

Graph of the difference  of the arguments of zrp and rzs depending on speciﬁc

values of n and K.

O8ARDELS is only on the CD.

Application 8.8.

1. Change the optical constants and plot a graph of  depending on a range of

values n for ﬁxed K and three values of θ, for example, 35

◦

, 45

◦

, 55

◦

2. Change the optical constants and plot a graph of  depending on a range of

K for ﬁxed value of n and three values of θ, for example, 35

◦

, 45

◦

, 55

◦

8.4. OPTICAL CONSTANTS OF METALS 335

APPENDIX 8.1

A8.1.1 Analytical Expressions and Approximations for the

Determinaton of

n and K

As discussed in Section 3.2 there are approximate methods to represent n and

K analytically. We show that an approximation is used to get formulas for n

and K depending on the ratio of r

to r

, the phase difference  of r

and r

after reﬂection, and the angle of incidence θ. This method is called ellipsometry

because one measures the absolute value of the ratio r

to r

and the phase

difference  of r

and r

; see Section 8.4.6. Using the law of refraction one may

rewrite Fresnel’s formulas for ratios r

and r

 (−1) sin(θ − θ



)/sin(θ + θ



) (A8.1)

 tan(θ −θ



)/ tan(θ +θ



), (A8.2)

and obtain for r

−{cos(θ − θ



)/ cos(θ + θ



)}. (A8.3)

The ratio r

may be complex, and therefore we call P the absolute value of

the ratio r

, and  the argument.

−i

 r

−cos(θ − θ



)/ cos(θ + θ



). (A8.4)

Using the formula for the sum and difference of angles in a cosine function one

may write

(1 − Pe

−i

)/(1 + Pe

−i

) −(cos θ cos θ



)/(sin θ sin θ



) (A8.5)

and with the complex law of refraction

(1 − Pe

−i

)/(1 + Pe

−i

)  (−1)





∗2

− (sin θ)

}/(sin θ)(tan θ ). (A8.6)

By using P  tan ψ one can write for the left side of Eq. (A8.6),

(1 − tan ψe

−i

)/(1 + tan ψe

−i

)

 (cos 2ψ + i sin  sin 2ψ)/(1 +cos  sin 2ψ) (A8.7)

and one has for Eq. (A8.7)





∗2

− (sin θ)

}

−(sin θ )(tan θ)(cos 2ψ + i sin  sin 2ψ)/(1 + cos  sin 2ψ). (A8.8)

We obtain for n



and K



the complex expression



+ iK





[(sin θ)

+{(sin θ)(tanθ)(cos 2ψ + i sin  sin 2ψ)/(1 + cos  sin 2ψ)}

(A8.9)

336 8. OPTICAL CONSTANTS

In order to get to n



and K



we have to determine the real and imaginary parts of

the right side of Eq. (A8.9). As done in Born and Wolf (1964, p. 619), one can

make an approximation by neglecting in the square root of Eq. (A8.8) the term

(sin θ)

with respect to n



∗2

, and obtain explicit expressions for n



and K



{(sin θ )(tan θ)(cos 2ψ)}/{1 + cos  sin 2ψ} (A8.10)



{(sin θ )(tan θ)(sin )(sin 2ψ)}/{1 + cos  sin 2ψ}. (A8.11)

We show in FileFig 8.9, graphs of P , , and ψ depending on the angle of

incidence θ. These graphs are for speciﬁc values of n and K. A comparison of

the exact and approximate calculation, again for speciﬁc values of n and K,is

shown in FileFig 8.10. In praxis one often uses iteration for the determination

of n



and K



and uses more than two input data for a best ﬁt calculation.

FileFig A8.9 (OA1DELTAFfS)

For zp  r

exp(iδ

) and zs  r

exp(iδ

), graphs are shown for P  tan ψ with

P  r

,  (difference of the arguments of r

and r

), and of atan(zs/zp).

OA1DELTAFfS is only on the CD.

Application A8.9.

1. Change the optical constants and plot a graph of P depending on a range of

values n for ﬁxed K and three values of θ, for example, 35

◦

, 45

◦

, 55

◦

2. Change the optical constants and plot a graph of atan(zs/zp) depending

values of on a range of K for ﬁxed value of n and three values of θ , for

example, 35

◦

, 45

◦

, 55

◦

FileFig A8.10 (OA2METPDS)

Graphs are shown for z  n + iK depending on ψ because one has P 

tan ψ, P  r

and  is the difference of the arguments of r

and r

. Curves

of the exact expressions are compared with the approximations.

OA2METPDS is only on the CD.

Application A8.10.

1. Study the approximation for different values of P and ﬁxed value of .

2. Study the approximation for different values of  and ﬁxed value of P .

8.4. OPTICAL CONSTANTS OF METALS 337

See also on the CD

PO1. Principal Angle. (see p. 315)

PO2. Oscillator. (see p. 317)

PO3. Sellmeir Expression. (see p. 319)

PO4. Drude Model. (see p. 322)

PO5. Skin Depth. (see p. 325)

PO6. Reﬂected Intensities. (see p. 328)

PO7. Phase Angle. (see p. 328)

CHAPTER

Fourier

Transformation and

FT-Spectroscopy

9.1 FOURIER TRANSFORMATION

9.1.1 Introduction

In this chapter we present some basic properties of Fourier transformation and

applications of Fourier transform spectroscopy. A simple example of an applica-

tion of Fourier transformation is the determination of the frequencies one needs

to compose a function f (x), presenting a rectangular pulse. Such a pulse may be

generated by superposition of many monochromatic waves with many different

wavelengths and amplitudes. The input data to Fourier transformation are the

space coordinates of f (x). The result of Fourier transformation is the frequency

spectrum corresponding to the different wavelengths used to compose f (x). A

more complicated application is the analysis of the interferogram obtained from

incident light traversing an absorbing material. The Fourier transformation of

the interferogram will calculate the absorption spectrum of the material.

The discussion uses a considerable number of examples and not much of the

mathematical theory of Fourier transformations. Most important is numerical

Fourier transformation, available in most computational computer programs and

applied in Fourier transform spectroscopy.

9.1.2 The Fourier Integrals

The integrals we used in the far ﬁeld approximation of the Kirchhoff–Fresnel

diffraction theory are Fourier integrals. The integral transforms the “input func-

tion" (in our case the aperture function), into the “output function" (in our case

the diffraction pattern). For the example of the diffraction at a slit, the aper-

ture function is the “(double) step function" S(y) and is transformed into the

339

340 9. FOURIER TRANSFORMATION AND FT-SPECTROSCOPY

diffraction pattern G(ν). The step function is deﬁned as

S(y) 

⎧

⎪

⎨

⎪

⎩

0 for ∞ to d/2

1 for d/2to − d/2

0 for − d/2to −∞,

(9.1)

and the Fourier integral transforms S(y) into the Fourier transform G(ν).

Using slightly different coordinates from those in Chapter 3, we have that the

Fourier transform of S(y)isG(ν).

G(ν) 

∞

∫

−∞

S(y)e

−i2πνy

dy. (9.2)

From Fourier transform theory we ﬁnd that the inverse relationship is also true

and we have the Fourier transform of (note the plus sign in the exponent)

S(y) 

∞

∫

−∞

G(ν)e

i2πνy

dν. (9.3)

Both variables ν and y have continuous valuesfrom −∞to +∞. The variable y is

the variable in the space domain and the variable ν is the variable in the frequency

domain and has the dimension of 1/space coordinate. (In infrared spectroscopy

one uses as the unit cm

−1

). Both G(ν) and S(y) are not normalized. When G(ν)

is symmetric with respect to zero, the integral may be written as

S(y)  2

∞

∫

G(ν) cos(2πνy)dν. (9.4)

We now discuss some analytical Fourier transformations.

9.1.3 Examples of Fourier Transformations Using Analytical

Functions

We present two examples to calculate the Fourier transformation, and the Fourier

transformation of the Fourier transformation. We show that the latter is indeed

the original function.

9.1.3.1 Gauss Function

We consider

S(y)  exp(−a

/2). (9.5)

We insert it into the integral of Eq. (9.2) and use the integral formula

∞

∫

exp(−c

) cos(bx)dx  (

√

π/2c) exp(−b

/4c

) (9.6)

and obtain

G(ν)  (

√

2π/a) exp(−2π

). (9.7)