Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple

Подождите немного. Документ загружается.

9.1. FOURIER TRANSFORMATION 341

If we take the function G(ν)  (

√

2π/a) exp(−2π

) and insert it into

Eq. (9.3) and use the same integral formula, we get back the original function

S(y):

S(y)  exp(−a

/2). (9.8)

This example shows that the Fourier transformation of the Fourier transformation

reproduces the original function.

9.1.3.2 The Functions

1/(1 + x

) and πe

−2πν

If we use

S(y)  1/(1 + y

) (9.9)

and apply the integral formula

∞

∫

{(cos ax)/(1 +x

)}dx  (π/2)e

−a

, (9.10)

we obtain

G(ν)  πe

−2πν

, (9.11)

and for the Fourier transform of G(ν) we ﬁnd the original function by using the

integral formula

∞

∫

−ax

cos mxdx  a/(a

+ m

). (9.12)

As result we ﬁnd that the Fourier transform of 1/(1 + y

)isπe

−2πν

, and the

Fourier transform of πe

−2πν

is 1/(1 + y

−2πν

↔ 1/(1 + y

). (9.13)

These two examples are exceptions to the point of view that one may calculate

analytically the Fourier transformation and that one can get analytically the

inverse Fourier transformation. A simple example when this is not the case is

the Fourier transformation of the step function S(y) of Eq. (9.1). The Fourier

transformation is a function of the type (sin aν)/aν, and its Fourier transform may

not be calculated analytically because the result of the Fourier transformation of

(sin aν)/aν is a discontinuous function. However, using numerical methods, one

may perform the Fourier Transformation and the inverse Fourier transformation.

9.1.4 Numerical Fourier Transformation

9.1.4.1 Fast Fourier Transformation

For numerical calculations of Fourier transformations we use the fast Fourier

transformation program, available in most computational computer programs.

342 9. FOURIER TRANSFORMATION AND FT-SPECTROSCOPY

Real Fourier Transformation (ff t)

This program (ff t) is used for real input data and works with 2

input and 2

n−1

output points. For a real Fourier transformation we have, from Eq. (9.4),

S(y)  2

∞

∫

G(ν) cos(2πνy)dν. (9.14)

This integral may be written as

∫

−∞

G(ν) cos(2πνy)dν +

∞

∫

G(ν) cos(2πνy)dν. (9.15)

The ﬁrst term over the negative part of ν is the “mirror" image around 0 of the

second term overthe positive part. Negative frequencies are a formality in Fourier

transformations. They may be eliminated in order to correlate to observable

results.

The input data of the Fast Fourier transformation is arranged in such a way

that the negative part of the Fourier transformation follows the positive part. Let

us assume we have a total of 128 points. The positive part is from point 1 to 64,

and the negative part follows as a “mirror image" from 65 to 128. The frequency

content of the negative part is the same as that of the positive part. The fast

Fourier transformation therefore considers only one part, analyzes it, and plots

the determined frequencies for only 1/2 of the total points (in our example for

64 points). The inverse transformation (iff t ) works backward. It has 64 input

points, but takes care of the imaginary part and again ends up with 128 output

points. The Fourier transform program of Mathcad numbers 2

 64 points from

0 to 63, and 2

 128 points from 0 to 127.

We demonstrate in FileFig 9.1 the real Fourier transformation of a single-sided

step function with 256 points. For comparison in FileFig 9.2, we demonstrate the

real Fourier transformation of a double-sided step function with 256 points. Both

show the same transformation with 128 points, and the inverse transformation

for both is the original function.

FileFig 9.1 (F1FTSTEPS)

Real:The original function is a one-sided step function, 256 points.The transform

is a single-sided sin z/z function shown for 128 points. The inverse transforma-

tion reproduces the original function with 128 points. The imaginary part is

zero for the original, appears in the transform, and is zero again for the inverse

transformation.

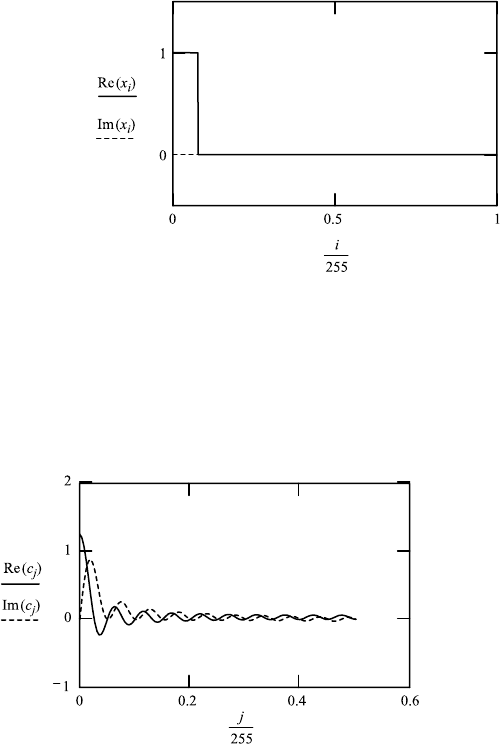
9.1. FOURIER TRANSFORMATION 343

F1FTSTEPS

Fourier Transform of a Single-Sided Step Function of Width 0 to d

The real FT is used. Orginal function

i : 0 ...255

: ((i) −(i − d)).

Global deﬁnition of d:

d ≡ 20.

Fourier transform

c : ff t(x)

N : last(c) N  128

j : 0 ...N.

The ﬁrst zero of FT is at 1/2d.

Fourier transform (inverse) of Fourier transform

y : iff t (c)

N : last(c) N  128

344 9. FOURIER TRANSFORMATION AND FT-SPECTROSCOPY

j : 0 ...N.

2 ·d

 0.025.

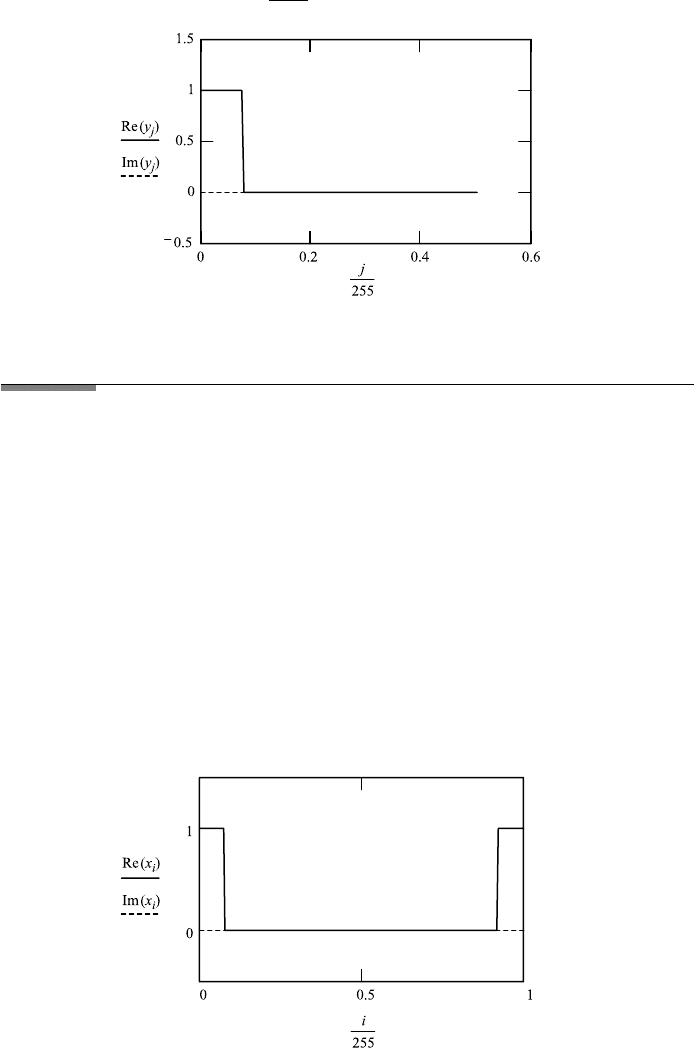
FileFig 9.2 (F2FTSTEPDS)

Real Fourier transformation: The Original Function is a double-sided step func-

tion, 256 points. The Fourier transform is a single-sided sin z/z function shown

for 128 points. The inverse transformation reproduces the original function. The

imaginary part is zero for the original, appears in the transform, and is zero

again for the inverse transformation.

F2FTSTEPDS

Fourier Transform of a Double-Sided Step Function of Width 0 to d

The real FT is used. Orginal function

i : 0 ...255

: [(i) −(i − d)] +(i − 255 + d).

9.1. FOURIER TRANSFORMATION 345

Fourier transform

c : ff t(x)

N : last(c) N  128

j : 0 ...N.

Global deﬁnition of d: d ≡ 20. The ﬁrst zero of FT is at 1/2d.

Fourier transform (inverse) of Fourier transform

y : iff t (c)

N : last(z) N 2  255

k : 0 ...N2

2 ·d

 0.025.

Complex Fourier Transformation (cf f t )

We saw in FileFigs 9.1 and 9.2 that the real Fourier transformation of the step

function, which is real, has a nonzero imaginary part. The imaginary part of the

transformations is different for the original single- and double-sided step func-

tions. To learn more about real and complex Fourier transformations, we apply

346 9. FOURIER TRANSFORMATION AND FT-SPECTROSCOPY

the complex Fourier transform in FileFig 9.3 to the single-sided step function

and in FileFig 9.4 to the double-sided step function.

The complex Fourier transformation program (cf f t ) works with 2

input

and 2

output points. The inverse transformation (icfft) works backwards with

input points and 2

output points. The imaginary part of the transformation

is again different for the single- and double-sided original step functions. The

inverse transformation reproduces the original function.

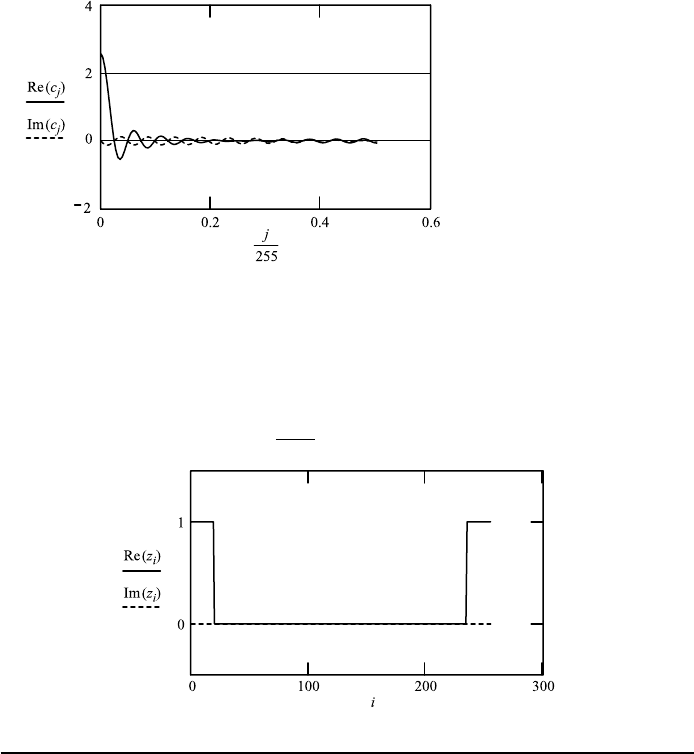
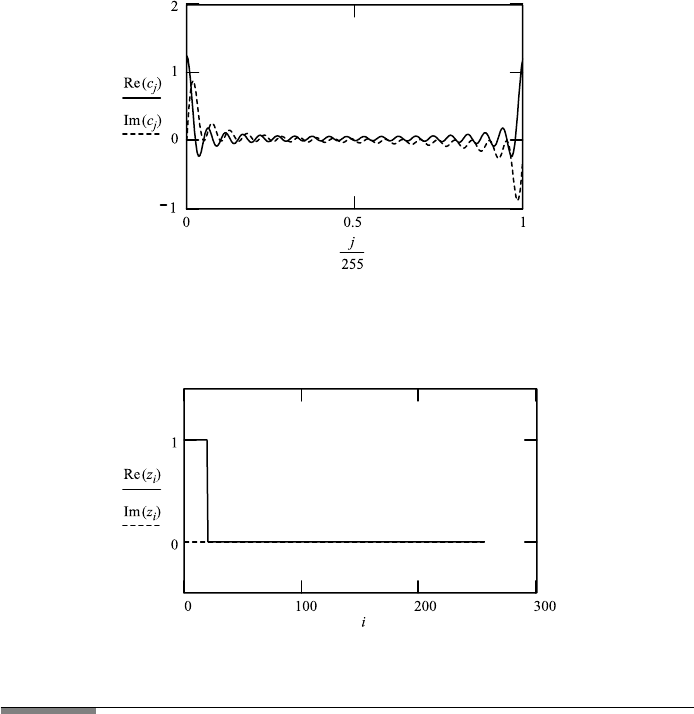
FileFig 9.3 (F3FTSTEPC1S)

Complex Fourier transformation: the original function is a one-sided step func-

tion, 256 points. The complex transformation is a double-sided sin z/z function

shown for all 256 points. The second part is a mirror image of the ﬁrst part. The

inverse transformation reproduces the original function. The imaginary part is

zero for the original, appears in the transform, and is zero again for the inverse

transform.

F3FTSTEPC1S

Fourier Transform of a Single-Sided Step Function of Width 0 to d

The complex FT is used. Orginal function

i : 0 ...255

: [(i) −(i − d)].

Global deﬁnition of d: d ≡ 20.

Fourier transform

c : cff t (x) N : last(c)

N  255 j : 0 ...N.

9.1. FOURIER TRANSFORMATION 347

Fourier transform (inverse) of Fourier transform

y : ff t(c) N : last(z)

N2  255 k : 0 ...N2.

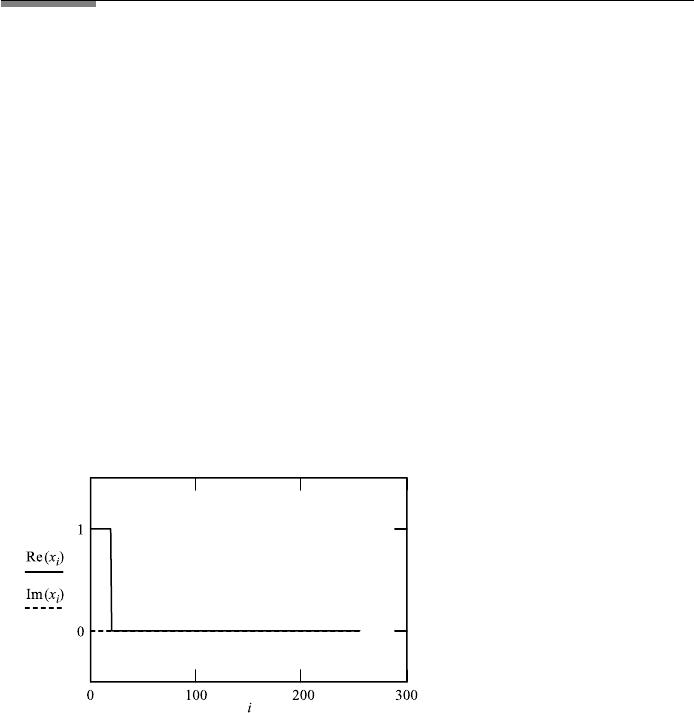
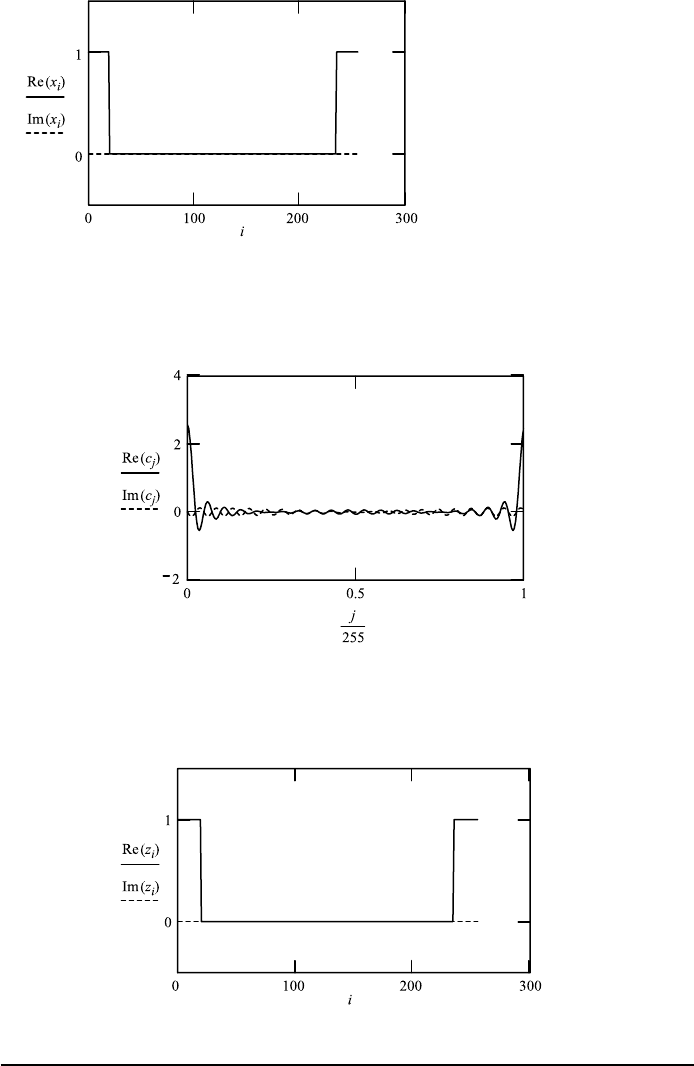
FileFig 9.4 (F4FTSTEPOSS)

Complex Fourier transformation; the original function is a double-sided step

function, 256 points. The complex transformation is a double-sided sin x/x func-

tion shown for all 256 points. The second part is a mirror image of the ﬁrst part.

The inverse transformation reproduces the original function. The imaginary part

is zero for the original, appears in the transform, and is zero again for the inverse

transform.

F4FTSTEPOSS

Fourier Transform of a Double-Sided Step Function of Width 0 to d

The complex FT is used. Original function

i : 0 ...255

: [(i) −(i − d)] +(i − 255 + d).

348 9. FOURIER TRANSFORMATION AND FT-SPECTROSCOPY

Global deﬁnition of d: d ≡ 20.

Fourier transform

c : cff t (x) N : last(c)

N  255 j : 0 ...N.

Fourier transform (inverse) of Fourier transform

z : icfft(c) N 2: last(z)

N2  255 k : 0 ...N2.

9.1. FOURIER TRANSFORMATION 349

In FileFigs.5 and 6 we compare real and complex Fourier transformations

for the sin x/x function, and observe the difference in the second graphs of the

FileFigs.5 and 6.

FileFig 9.5 (F5FTSINCRS

Real Fourier transformation:the original function is a one sided sin x/x function,

256 points. The real transformation is a single-sided step function shown for

128 points. The real inverse transformation reproduces the original function.

The imaginary part is zero for the original, appears in the transform, and is zero

again for the inverse transform.

F5FTSINCRS is only on the CD.

FileFig 9.6 (F6FTSINCCS)

Complex Fourier transformation: the original function is a one-sided sin x/x

function, 256 points. The complex transform is a double-sided step function

shown for 256 points. The complex inverse transformation reproduces the origi-

nal function.The imaginary part is zero for the original, appears in the transform,

and is zero again for the inverse transform.

F6FTSINCCS is only on the CD.

9.1.4.2 General Fourier Transformation

The fast Fourier transformation needs 2

input points. In the case where we

have a different number of input points we have to use the complex Fourier

transformation and its inverse. In FileFig 9.7 we show the complex Fourier

transformation for the step function using 184 points, and in FileFig 9.8 for the

sin z/z function.

FileFig 9.7 (F7FTSTEP183S)

The original function is a step function. The number of points is 184. The complex

Fourier transformation results in a double-sided sin z/z function. The inverse

complex transformation reproduces the original function. The imaginary part is

zero for the original, appears in the transform, and is zero again for the inverse

transform.

F7FTSTEP183S is only on the CD.

350 9. FOURIER TRANSFORMATION AND FT-SPECTROSCOPY

FileFig 9.8 (F8FTSINC183S)

The original function is a sin z/z function. The number of points is 184. The

complex Fourier transformation results in a double-sided step function. The

inverse complex transformation reproduces the original function. The imaginary

part is zero for the original, appears in the transform, and is zero again for the

inverse transform.

F8FTSINC183S is only on the CD.

A comparison of the fast Fourier transformation with the general Fourier

transformation is givenin FileFigs.9 and 10. The complex Fourier transformation

of a Gauss functions with different a values is given in FileFig 9.9 for 256 points,

and in FileFig 9.10 for 326 points.

FileFig 9.9 (F9FTGAUSS)

The original function is the Gauss function with values of 50 and 100 for a. The

number of points is 256. The complex Fourier transformation again results in

a Gauss function, however, with a narrower shape. The inverse transformation

reproduces the original function. The imaginary part is zero for the original,

appears in the transform, and is zero again for the inverse transform.

F9FTGAUSS is only on the CD.

FileFig 9.10 (F10FTGAUSGS)

The original function is the Gauss function with values of 50 and 100 for a. The

number of points is 326. The complex Fourier transformation again results in

a Gauss function, however, with a narrower shape. The inverse transformation

reproduces the original function. The imaginary part is zero for the original,

appears in the transform, and is zero again for the inverse transform.

F10FTGAUSGS is only on the CD.

9.1.5 Fourier Transformation of a Product of Two Functions

and the Convolution Integral

The Fourier transformation S(y) of the function G(ν)is

S(y) 

+∞

∫

−∞

G(ν)expi2πνydν. (9.16)