Moller K.D. Optics. Learning by Computing, with Examples Using Mathcad, Matlab, Mathematica, and Maple
Подождите немного. Документ загружается.

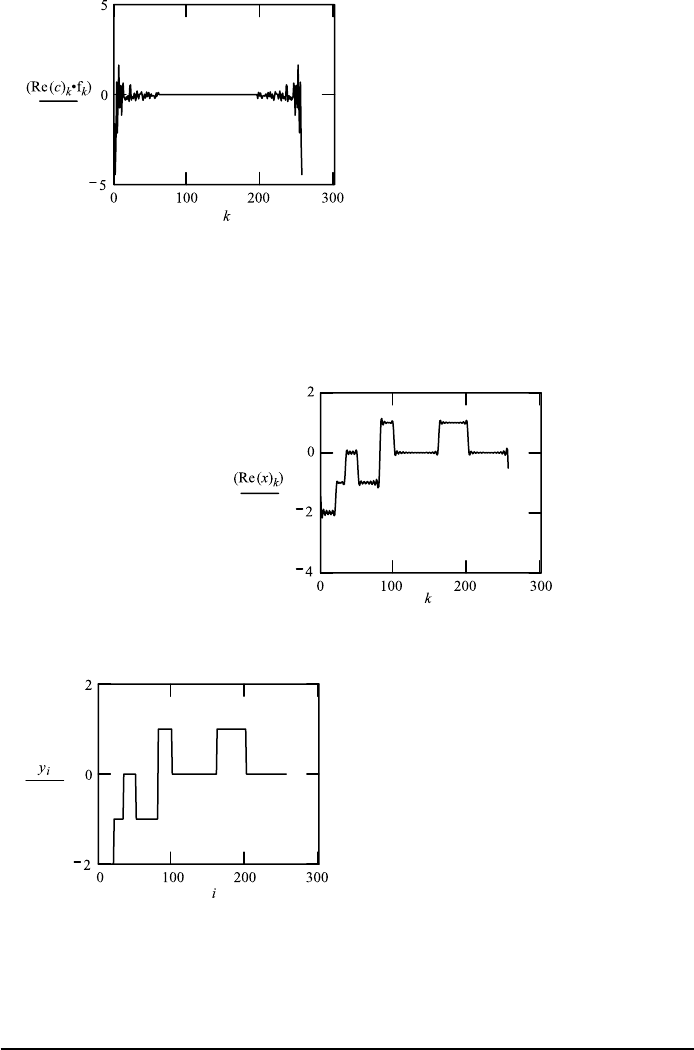
412 10. IMAGING USING WAVE THEORY
The product: hologram × filter
The FT (inverse) of the changed hologram (hologram × filter), similar to the
object
ccc
k
: c
k
· f
k
x : icff t(ccc) N : last(ccc) N 255
k : 0 ...255.
For comparison: the object
Application 10.18. Observe the changes of the size of the hologram when mak-
ing the range of passing low frequencies larger or smaller. The blocking function
and the final image may be modified by changing a and b.
10.6. HOLOGRAPHY 413
See also on the CD
PW1. Fourier Series. (see p. 370)
PW2. Two Bars. (see p.381)
PW3. Two round Objects. (see p. 383)
PW4. Demonstration of the use of Spread Function (siny/y)
2
as a Transfer
Function. (see p. 386)
PW5. Demonstration of the use of Spread Function (J1(y)/y)
2
as a Transfer
Function. (see p. 386)
PW6. Rayleigh Distance and Resolution with incoherent Light. (see p. 389)
PW7. Rayleigh Distance and Resolution with coherent Light. (see p. 392)
PW8. Transfer Function for (sinx/x) of the Coherent Case. (see p. 394)
PW9. Transfer Function for (Bess/arg) of the Coherent Case. (see p. 394)
PW10. Blocking Function for removing high Frequencies. (see p. 399)
PW11. Blocking Function passing a band of Frequencies. (see p. 399)
PW12. Blocking Function passing periodic portion of all Frequencies. (see p.
400)
PW13. Size of Hologram and Quality of Image. (see p. 402)

11
11
CHAPTER
Aberration
11.1 INTRODUCTION
In Chapter 1 on Geometrical Optics we discussed geometrical image formation
by using paraxial theory. The essential assumption of paraxial theory is that
the angles between an emerging ray from the object and the axis of the system
are small. In general small means that one could replace sin α by the angle α
(in radians). When this assumption can not be made, one obtains a distorted
image. There are elaborate computational programs available for lens design,
including systematic corrections for the various types of aberrations. To give
an introduction to the most commonly known monochromatic aberrations, we
discuss spherical aberration of a single refracting surface and a thin lens, and
coma, and astigmatism of a spherical surface and a thin lens. At the end we also
discuss chromatic aberration.
11.2 SPHERICAL ABERRATION OF A SINGLE
REFRACTING SURFACE
In Figure 11.1, two rays are shown from the object point P
1
to the spherical
surface. After refraction one ray is connected to the image point P
2
, the other to
P
2
. When paraxial theory can not be used, the ray with the larger angle α
2
has
the image point P
2
closer to the refracting surface. The difference between the
points P
2
and P
2
is called the longitudinal spherical aberration.Forits derivation,
we look at Figure 11.2 and derive the relations for image formation at one
spherical surface
(s
1
+ r)/(sin(180 − θ
1
) ζ
1
/ sin β (11.1)
415
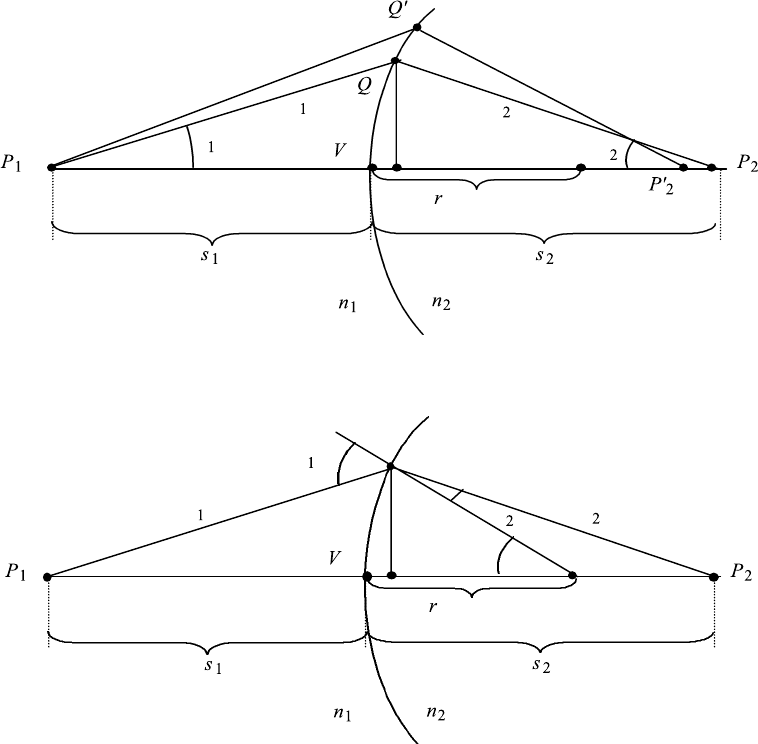
416 11. ABERRATION
ρ
ζ
ζ
α
α
ε
FIGURE 11.1 Spherical aberration of a single surface. The image point P
2
is formed by the paraxial ray
P
1
QP
2
. The marginal ray P
1
Q
P
2
forms the image at P
2
, a position closer to the lens.
β
ρ
θ
θ
ζ
ζ
FIGURE 11.2 Coordinates for the treatment of spherical aberration of a single surface.
and
(s
2
− r)/ sin θ
2
ζ
2
/ sin(180 − β). (11.2)
Equations (11.1) and (11.2) may be combined to form
(s
1
+ r)/(s
2
− r) nζ
1
/ζ
2
, (11.3)
where n is the refractive index of the refracting medium. To get expressions for
ζ
1
and ζ
2
, we look at the triangle P
1
QP
2
(Figure 11.2) and have
ζ
2
1
r
2
+ (s
1
+ r)
2
− 2r(s
1
+ r) cos β. (11.4)
Expanding cos β 1 − β
2
/2 and setting β ρ/r one gets
ζ
2
1
r
2
+ (s
1
+ r)
2
− 2r(s
1
+ r)(1 −[ρ
2
/2r
2
]), (11.5)
11.2. SPHERICAL ABERRATION OF A SINGLE REFRACTING SURFACE 417
which results in
ζ
2
1
s
2
1
+ (s
1
+ r)[ρ
2
/r]. (11.6)
Similarly one obtains
ζ
2
2
s
2
s
− (s
2
− r)[ρ
2
/r]. (11.7)
Expanding the root one has
ζ
1
s
1
+ (1/s
1
+ 1/r)[ρ
2
/2] (11.8)
ζ
2
s
2
+ (1/s
2
− 1/r)[ρ
2
/2]. (11.9)
Introduction of Eqs. (11.8) and (11.9) into (11.3) results in
(s
1
+ r)/(s
2
− r)
n{s
1
+ (1/s
1
+ 1/r)[ρ
2
/2]}/{s
2
+ (1/s
2
− 1/r)[ρ
2
/2]}. (11.10)
This equation may be rewritten as
1/s
1
+ n/s
2
+ (1 − n)/r
(1/r + 1/s
1
)(1/r − 1/s
2
)(n/s
1
+ 1/s
2
)[ρ
2
/2]. (11.11)
Introduction of s
1
−x
0
and s
2
x
i
results in
− 1/x
0
+ n/x
i
+ (1 − n)/r
(1/r − 1/x
0
)(1/r − 1/x
i
)(1/x
i
− n/x
0
)[ρ
2
/2]. (11.12)
In the limit of ρ → 0 we must get back to the imaging equation of paraxial
theory,
−1/x
0
+ n/x
i1
+ (1 − n)/r 0, (11.13)
where we have written x
i1
for the image distance for the paraxial case. The
coefficient of correction on the right side of Eq. (11.12) depends on x
0
and x
i
.
To have it depending only on x
0
, we use Eq. (11.13), eliminating x
i
and get
n/x
i1sal
1/x
0
+ (n − 1)/r + ((n − 1)/n
2
)(1/r − 1/x
0
)
2
(1/r − (n + 1)/x
0
))[ρ
2
/2],
(11.14)
where we have written x
i1sal
to indicate the image distance for the longitudinal
spherical aberration of a surface of radius of curvature ρ.
The longitudinal spherical aberration (LSA) is defined as x
i1
−x
i1sal
, which is
the difference of the image positions calculated for the paraxial and the spherical
aberration cases. In FileFig 11.1, we study the LSA for an object distance, which
corresponds to a real image, and two different refractive indices. In FileFig 11.2,
we study the dependence of LSA on object distances, which corresponds to real
images, and on the refractive index and the radius of curvature. For real images
spherical aberration may not be eliminated.

418 11. ABERRATION
FileFig 11.1 (A1SPHASS)
Calculation of LSA x
i1
− x
i1sal
for a single spherical surface and negative
object distance for two different refractive indices.
A1SPHASS is only on the CD.
Application 11.1.
1. Consider positive and negative object distances and choose one refractive
index. Show that one can get positive and negative values for the LSA.
2. Decide how small you want to make the LSA and determine the corresponding
value of n.
FileFig 11.2 (A2SPASSS)
Calculations for a single spherical surface to demonstrate the dependence of
LSA x
i1
−x
i1sal
on the object position, the refractive index, and the radius of
curvature. Note that for the choice of parameters used, there is no value of the
refractive index for which the LSA is zero.
A2SPASSS is only on the CD.
11.3 LONGITUDINAL AND LATERAL SPHERICAL
ABERRATION OF A THIN LENS
In Figure 11.3 spherical aberrations are shown for a positive and a negative thin
lens. To calculate the LSA x
i1
− x
sph
for a thin lens we use twice the result
obtained for a single spherical surface, as discussed in Section 11.2. There we
calculated for a spherical surface with refractive index n, the position x
i1sal
(see
Eq. (11.14)). The light entered from the medium of index 1 and traveled into the
medium of index n. We obtained
− 1/x
0
+ n/x
i
(11.15)
(n − 1)/r
1
+ ((n − 1)/n2)(1/r
1
− 1/x
0
)
2
(1/r
1
− (n + 1)/x
0
)[ρ
2
/2].
This result may be used to get a similar expression for light incident on the second
surface traveling from the medium with index n into the medium of index 1. We
substitute x
0
with → x
ii
and x
i
with → x
00
and obtain
− n/x
00
+ 1/x
ii
(11.16)
−(n − 1)/r
2
− ((n − 1)/n2)(1/r
2
− 1/x
ii
)
2
(1/r
2
− (n + 1)/x
ii
)[ρ
2
/2],

11.3. LONGITUDINAL AND LATERAL SPHERICAL ABERRATION OF A THIN LENS 419
FIGURE 11.3 (a) Spherical aberration for a positive lens, real image points; (b) spherical aberration
for a negative lens, virtual image points.
where x
i
and x
00
are the same points when considering the case of a thin lens.
Addition of Eqs. (11.15) and (11.16) will eliminate the terms n/x
i
and −n/x
00
,
and results in
− 1/x
0
+ 1/x
ii
(11.17)
(n − 1)/r
1
+ ((n − 1)/n
2
)(1/r
1
− 1/x
0
)
2
(1/r
1
− (n + 1)/x
0
)[ρ
2
/2]
− (n − 1)/r
2
− ((n − 1)/n
2
)(1/r
2
− 1/x
ii
)
2
(1/r
2
− (n + 1)/x
ii
)[ρ
2
/2].
To calculate x
ii
one uses the paraxial equation of the thin lens
1/x
ii
1/x
0
+ (n − 1)(1/r
1
− 1/r
2
), (11.18)
where
1/f (n − 1)(1/r
1
− 1/r
2
) (11.19)
and finally we have
− 1/x
0
+ 1/x
iisph
(11.20)
(n − 1)(1/r
1
− 1/r
2
) + ((n − 1)/n
2
)[(1/r
1
− 1/x
0
)
2
(1/r
1
− (n + 1)/x
0
)
− (1/x
0
+ (n − 1)/r
1
− n/r
2
)
2
(n
2
/r
2
− (n + 1)/x
0
− (n
2
− 1)/r
1
)][ρ
2
/2].
The longitudinal spherical aberration of a thin lens is defined as LSA x
ii
−
x
iisph
. We call the right side of Eq. (11.20) the reciprocal focal length for the
420
11. ABERRATION
spherical aberration case, 1/f f (x
0
), where ff (x
0
) is the focal length of the case
of spherical aberration. The result is
−1/x
0
+ 1/x
iisph
1/ff (x
0
) (11.21)
with
ff (x
0
) 1/{1/f +{(n − 1)/n
2
}[ρ
2
/2]{a(x
0
) − b(x
0
)c(x
0
)}} (11.22)
and the abbreviations
a(x
0
) [(1/r
1
− 1/x
0
)
2
(1/r
1
− (n + 1)/x
0
)],
b(x
0
) [1/x
0
+ (n − 1)/r
1
− n/r
2
]
2
(11.23)
c(x
0
) [n
2
/r
2
− (n + 1)/x
0
− (n
2
− 1)/r
1
].
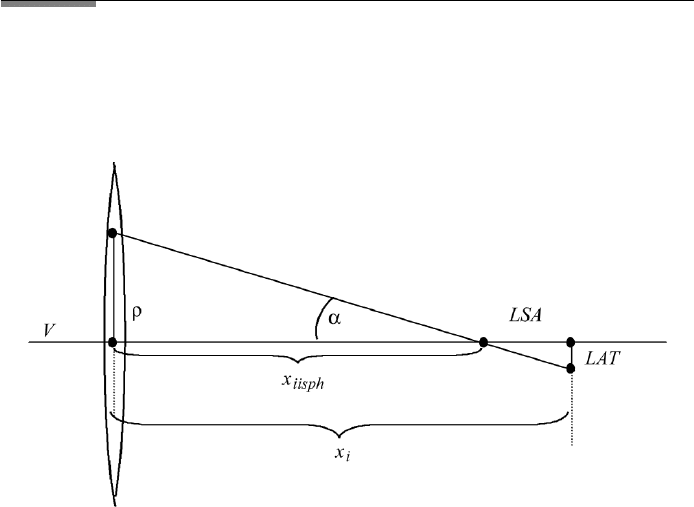
In Figure 11.4 we define the lateral spherical aberration as LAT LSA times
ρ/x
iisph
. In FileFig 11.3 we study the question of elimination of spherical aber-
ration and calculate numerical values of LSA and LAT for a choice of parameters
of n, r
1
, r
2
, ρ, and object distance x
0
. The elimination of spherical aberration is
further discussed in the next section using the π–σ equation.
FileFig 11.3 (A3SPHTINS)
Calculations of the spherical aberration of a thin lens. Longitudinal spherical
aberration and lateral spherical aberration.
A3SPHTINS is only on the CD.
FIGURE 11.4 Longitudinal spherical aberration (LSA). The lateral spherical aberration (LAT) is
calculated using tan α.

11.4. THE π –σ EQUATION AND SPHERICAL ABERRATION 421
Application 11.3.
1. Use different values of n and observe that spherical aberration may not be
eliminated for real objects and images.
2. Assume x
0
values for virtual images and find positive and negative values for
the LSA. Therefore, for this case, spherical aberration may be eliminated.
11.4 THE π–σ EQUATION AND SPHERICAL
ABERRATION
We now study whether spherical aberration can be removed when using a special
choice of parameters. We introduce the parameters π (position factor) and σ
(shape factor),
π (x
ii
+ x
0
)/(x
ii
− x
0
) and σ (r
2
+ r
1
)/(r
2
− r
1
). (11.24)
Using Eqs. (11.18) and (11.19) we may write
1/x
0
−(π + 1)/2f and 1/x
i
(1 − π )/2f (11.25)
1/r
1
(σ + 1)/{2f (n − 1)} and 1/r
2
(σ − 1)/{2f (n − 1)}. (11.26)
Introducing the expressions of Eqs. (11.24) to (11.26) into Eq. (1.17) we get
− 1/x
0
+ 1/x
iisph
(n − 1)(1/r
1
− 1/r
2
) + [ρ
2
/f
3
]{Aσ
2
+ Bσπ + Cπ
2
+ D}, (11.27)
where we abbreviated
A (n + 2)/{8n(n − 1)
2
} B (n +1)/{2n(n − 1)} (11.28)
C (3n +2)/(8n) D n
2
/{8(n − 1)
2
}. (11.29)
We may look at Eq. (11.27) as the thin lens equation plus a correction term. To
study whether spherical aberration can be removed we look at the correction
term
Y [ρ
2
/f
3
]{Aσ
2
+ Bσπ + Cπ
2
+ D}. (11.30)
When Y is equal to zero, spherical aberration is eliminated.
In FileFig 11.4 a graph is shown for f 10, n 1.5, ρ 4, and x
0
4.
There are Y values smaller than zero and, using these parameters, spherical
aberration may be eliminated. In FileFig 11.4 one may study an example for
positive and negative values of x
0
and ρ between 1 and 4. When Y shows negative
values, spherical aberration may be eliminated.
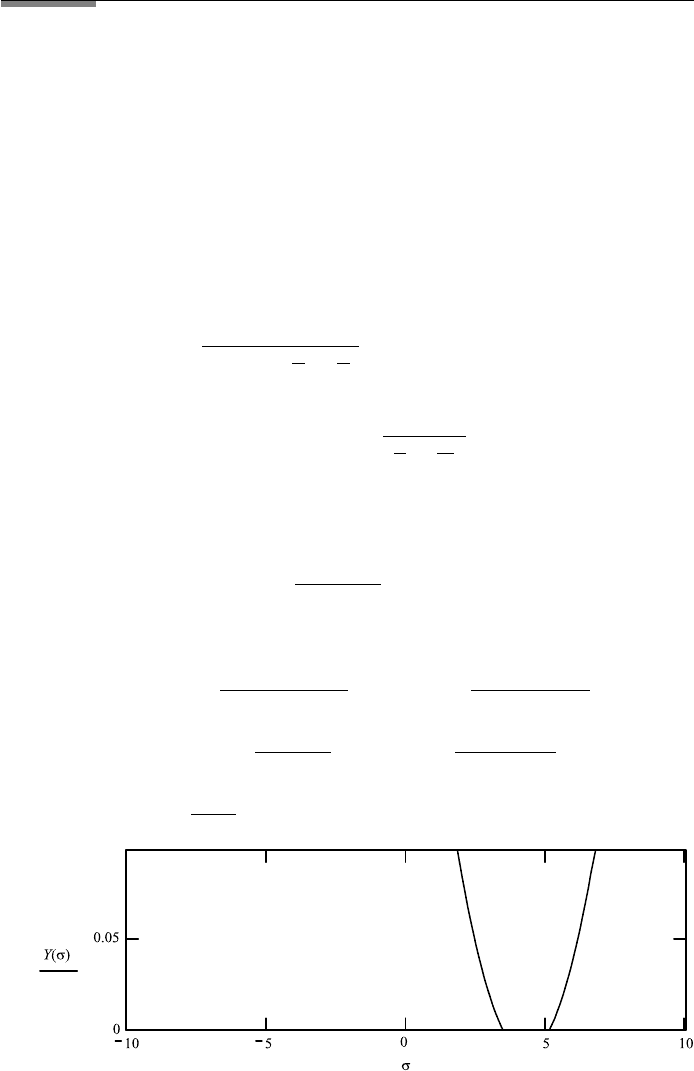
422 11. ABERRATION
FileFig 11.4 (A4SPHLSIPIS)
The π–σ equation and spherical aberration for the thin lens. The graph shown is
for ρ 1 and x
0
−11, and one only has positive values of Y (σ ). This means
spherical aberration is not eliminated.
A4SPHLSIPIS
Spherical Aberration and the π − σ Equation
We assume n 1.5 and compare the cases of real and virtual images.
1. Image for f 10, and xo to the left of focal point, LSA may not be eliminated
f :
1
(n − 1) · (
1
r
1
−
1
r
2
)
r
1
≡ 10 r
2
≡−10 n ≡ 1.5
ro ≡ 4 xo ≡ 4
f 10 xi :
1
1
f
+
1
xo
xi 2.857.
2. Definitions
σ (r
2
+ r
1
)/(r
2
− r
1
) σ :−10, −9.9 ...10
π :
xi + xo
(xi − xo)
π −6.
3. π–σ Equation
A(n):
n + 2
8 · n · (n − 1)
2
B(n):
n + 1
2 ·n · (n − 1)
C(n):
3 · n + 2
8 · n
D(n):
n
2
8 · (n − 1)
2
Y (σ ):
(ro)
2
f
3
· (A(n) · σ
2
+ B(n)σπ + C(n)π
2
+ D(n)).
