Моклячук М.П., Ямненко Р.Є. Лекції з теорії вибору та прийняття рішень (на укр. языке)

Подождите немного. Документ загружается.

5.3. ВТРАТИ ПРОПОРЦIЙНI АБСОЛЮТНIЙ ВЕЛИЧИНI

ПОХИБКИ

Припустимо, що збиток пропорцiйний абсолютнiй величинi похибки.

Нехай при ω ∈ R

та d ∈ R

збиток L(ω,d) має вигляд

L(ω,d)=a|ω − d|. (5.3.1)

Якщо функцiя втрат задається формулою (5.1.1), то байєсiвське рiшен-

ня d

∗

при довiльно заданому розподiлi W визначається, як число d,яке

мiнiмiзує математичне сподiвання E(|W − d|).

Кажуть, що число m –цемедiана розподiлу W ,якщоP(W ≥ n) ≥ 1/2

i P(W ≤ m) ≥ 1/2. Кожний розподiл має принаймнi одну медiану, але не

обов’язково єдину.

Наступна теорема показує, що медiана розподiлу W буде байєсiвською

оцiнкою параметра для функцiї втрат (5.3.1).

Теорема 5.3.1. Нехай E(|W | < ∞.Числоd

∗

задовольняє спiввiдношення

E(|W − d

∗

|)= inf

−∞<d<∞

E(|W − d|) (5.3.2)

тодi i тiльки тодi, коли d

∗

– медiана розподiлу W .

Доведення. Нехай d

∗

– медiана розподiлу W ,аd – довiльне iнше число.

Тодi

E(|W − d|)=



E(|W − d

∗

|)+2



∗

(d − x)dF (x), при d>d

∗

E(|W − d

∗

|)+2



∗

(x − d)dF (x), при d<d

∗

(5.3.3)

Приклад 5.3.1. Розглянемо повторну вибiрку X

,...,X

знормального

розподiлу з невiдомим значенням середнього W i заданою мiрою точно-

стi r. Припустимо, що потрiбно оцiнити значення W при функцiї втрат

(5.3.1). При пiдходящому виборi системи одиниць в цiй рiвностi a =1.

З теореми 4.4.1 випливає, що якщо апрiорний розподiл W нормальний

зсереднiмµ та мiрою точностi τ, то для довiльних значень X

,...,X

апостерiорний розподiл W нормальний з середнiм



τµ+ nr



/(τ + nr)

та мiрою точностi τ + nr. Оскiльки єдина медiана нормального розподiлу

спiвпадає з його середнiм, то байєсiвська оцiнка δ

∗

визначається насту-

пним чином:

∗

,...,X

τµ+ nr

τ + nr

. (5.3.4)

Байєсiвський ризик ρ

∗

(p) дорiвнює

∗

(p)=E [|W − δ

∗

,...,X

) |] . (5.3.5)

231

Апостерiорний розподiл випадкової величини [W −δ

∗

,...,X

)] при

= x

,i =1,...,n, буде нормальним з середнiм 0 та мiрою точностi τ+nr,

незалежно вiд значень x

,...,x

.Далi,якщоY – нормальна випадкова

величина з середнiм 0 та мiрою точностi τ,то

E|Y | =



πτ



. (5.3.6)

Отже, для довiльних значень X

,...,X

середнє значення у правiй частинi

(5.3.5) дорiвнює (2/ [π(τ + nr)])

1/2

. Iз спiввiдношення (5.3.5) випливає,

що

∗

(p)=

π(τ + nr)

. (5.3.7)

Припустимо тепер, що цiна одного спостереження дорiвнює c (c>0) i

статистик може вибирати об’єм вибiрки. З рiвностi (5.3.7) видно, що для

вибiрки об’ємом n загальний ризик дорiвнює

π(τ + nr)

+ cn (5.3.8)

i вiн мiнiмiзується при

n =

(2πrc

)

−

. (5.3.9)

Зрозумiло, що число повинно бути невiд’ємним та цiлим. Якщо τ → 0,то

граничне значення в рiвностi (5.3.9) буде оптимальним значенням числа

спостережень в цiй задачi для випадку, коли апрiорна iнформацiя щодо

W незначна.

5.4. ОЦIНЮВАННЯ ВЕКТОРНОГО ПАРАМЕТРА

Розглянемо задачу оцiнювання вектора

W =(W

,...,W

)

при k ≥ 2. Стандартною функцiєю втрат для такої задачi є квадратична

функцiя втрат L,якавизначенадлявсiхw ∈ R

та d ∈ R

за формулою

L(w,d)=(w − d)



A(w − d). (5.4.1)

Тут A – симетрична невiд’ємно визначена k ×k матриця. Якщо A –дода-

тно визначена матриця, то кожному ненульовому вектору похибок w − d

вiдповiдає додатнiй збиток. З iншого боку, якщо матриця A не є додатно

визначеною, то iснують ненульовi вектори похибок з нульовими втрата-

ми. Такi вектори iснують, наприклад, якщо статистик цiкавиться оцiнкою

232

лише декiлькох компонент W, а значення iнших компонент для нього

несуттєвi i розглядаються як заважаючi параметри.

Припустимо, що для W iснує вектор середнiх i коварiацiйна матриця,

E(W)=µ iCov(W)=Σ. Байєсiвська оцiнка при заданому розподiлi W

–цеточкаd ∈ R

, яка мiнiмiзує математичне сподiвання

E[(W − d)



A (W − d)] =

= E{[(W − µ)



+(µ − d)



] A [(W − µ)+(µ − d)]} =

= E[(W − µ)



A (W − µ)] + (µ − d)



A(µ − d). (5.4.2)

У правiй частинi спiввiдношення (5.4.2) рiшення d не входить пiд знак

математичного сподiвання. Оскiльки A – невiд’ємно визначена матриця,

то другий доданок правої частини невiд’ємний для всiх значень d.Отже,

d ∈ R

– байєсiвська оцiнка тодi i тiльки тодi , коли

(µ − d)



A(µ − d)=0. (5.4.3)

Звiдси випливає, що значення d = µ єбайєсiвськоюоцiнкоюдляW.

Далi, якщо A – додатно визначена матриця, то це значення d буде єди-

ноюбайєсiвськоюоцiнкою.ЯкщоматрицяA не є додатно визначеною,

то знайдуться iншi значення d, якi задовольняють спiввiдношення (5.4.3).

Пiдкреслимо, що вектор середнiх µ = E(W) завжди є байєсiвською оцiн-

кою для довiльної симетричної невiд’ємно визначеної матрицi A.

Можна показати, що

E[(W − µ)



A (W − µ)] = tr(AΣ), (5.4.4)

де Σ – коварiацiйна матриця для W розмiрностi k ×k.Отже,зiспiввiдно-

шення (5.4.2) випливає, що математичне сподiвання збитку для довiльної

байєсiвської оцiнки d дорiвнює tr(AΣ).

Нехай X – спостереження з умовною щiльнiстю розподiлу f (·|w) при

W = w. З викладеного вище зрозумiло, що байєсiвська розв’язуюча фун-

кцiя δ

∗

визначається рiвнiстю δ

∗

(X)=E(W|X) iбайєсiвськийризикρ

∗

(p)

при заданiй апрiорнiй щiльностi розподiлу p дорiвнює

∗

(p)=trace{A E[Cov (W|X)]}. (5.4.5)

Тут Cov (W|X) – коварiацiйна матриця апостерiорного розподiлу W при

заданому X.

Приклад 5.4.1. Нехай X

,...,X

– повторна вибiрка iз нормального роз-

подiлу, в якому середнє M iмiраточностiR невiдомi. Припустимо далi,

що при M = m i R = r та оцiнках -m i -r вiдповiдно для M i R збиток

задається наступним чином:

L(m,r, -m,-r)=a

(m − -m)

+ a

(r − -r)

+2a

(m − -m)(r − -r). (5.4.6)

233

Вимога невiд’ємної визначеностi матрицi A з (5.4.1) у випадку (5.4.6)

приймає вигляд: a

≥ 0 та a

≥ a

Припустимо, що апрiорний сумiсний розподiл M i R є нормальний–

гамма розподiл. Тодi апостерiорний розподiл M –цеt–розподiл з пара-

метром змiщення µ



, який вказаний у теоремi 4.4.3. Для того щоб дис-

персiя апостерiорного розподiлу була скiнченною, припустимо, що n>2.

Оскiльки щiльнiсть t–розподiлу симетрична вiдносно значення параметра

змiщення, то середнiм значенням апостерiорного розподiлу є µ



.Далi,з

тiєї ж теореми 4.4.3 видно, що апостерiорний розподiл R єгаммарозподiл

iз середнiм (2α + n)/(2β



), де значення β



наведене в теоремi. Iз сказаного

в цьому параграфi випливає, що байєсiвськими оцiнками для M та R є

середнi вказаних апостерiорних розподiлiв.

Зауваження. Ми показали, що в деяких задачах прийняття рiшень се-

реднє та медiана апостерiорного розподiлу одновимiрного параметру W

є байєсiвськими оцiнками. Для випадку векторного параметра W вектор

середнiх апостерiорного розподiлу також є байєсiвська оцiнка при квадра-

тичнiй функцiї втрат. Оскiльки не iснує стандартного визначення медiани

багатовимiрного розподiлу, то для випадку векторного параметра немає i

аналогiчних результатiв.

5.4.1. Задачi для самостiйної роботи

1. Нехай X

,...,X

– повторна вибiрка з розподiлу Пуассона з невi-

домим значенням середнього W , i нехай апрiорний розподiл W є

гамма-розподiл з параметрами α i β (α>0, β>0 ). Припустимо,

що потрiбно оцiнити значення W при функцiї втрат L, яка задає-

ться формулою (5.2.14). Доведiть, що байєсiвська оцiнка для W має

вигляд (5.2.15) i що байєсiвський ризик дорiвнює 1/(β + n).

2. Нехай X

,...,X

– повторна вибiрка з розподiлу Бернуллi, параметр

W якого невiдомий, i нехай апрiорний розподiл W єбета-розподiл

зпараметрамиα i β.Покажiть,щоякщозначенняW оцiнюється

при функцiї втрат L(ω,d)=(ω − d)

i цiна одного спостереження

дорiвнює c, то оптимальним числом спостережень буде

n =

αβ

c(α + β)(α + β +1)

1/2

− (α + β)

3. Нехай X

,...,X

– повторна вибiрка з нормального розподiлу з невi-

домим значенням середнього W i заданим значенням мiри точностi

234

r, причому апрiорний розподiл W нормальний з середнiм µ та мi-

рою точностi τ . Нехай потрiбно оцiнити значення W при функцiї

втрат L(ω,d)=(ω − d)

та цiнi c за спостереження. Покажiть, що

оптимальним числом спостережень буде

n =





1/2

−

4. Нехай X

,...,X

– повторна вибiрка з рiвномiрного розподiлу на

iнтервалi (0,W ), де значення W невiдоме i апрiорний розподiл W є

розподiлом Парето з параметрами ω

i α (α>2). Покажiть, що якщо

значення W оцiнюється при функцiї втрат L(ω,d)=(ω − d)

та цiнi

одного спостереження c, то оптимальний об’єм вибiрки n задається

формулою

n =

2αω

c(α − 2)

1/3

− (α −1)

5. Нехай W – випадкова величина з функцiєю розподiлу G,причому

E(|W |

) < ∞, α>1. Доведiть, що математичне сподiвання E(|W −

) мiнiмiзується при d, яке дорiвнює тому єдиному числу, для

якого



ω<d

(d − ω)

α−1

dG(ω)=



ω>d

(d − ω)

α−1

dG(ω).

6. Нехай W – параметр, який оцiнюється при функцiї втрат

L(ω,d)=



ω −d



Нехай E(W

) < ∞.Покажiть,щоякщоE(W ) =0,тобайєсiвська

оцiнка d задається рiвнiстю

d =

E(W

)

E(W )

аякщоE(W )=0i E(W

) > 0, то байєсiвська оцiнка не iснує. Далi,

покажiть, що в будь-якому випадку байєсiвський ризик ρ

∗

задається

формулою

∗

Var(W )

E(W

)

7. Припустимо, що W – параметр, який оцiнюється при функцiї втрат

вигляду

L(ω,d)=



(ω − d)

(d − ω)

при

d ≤ ω,

d ≥ ω.

235

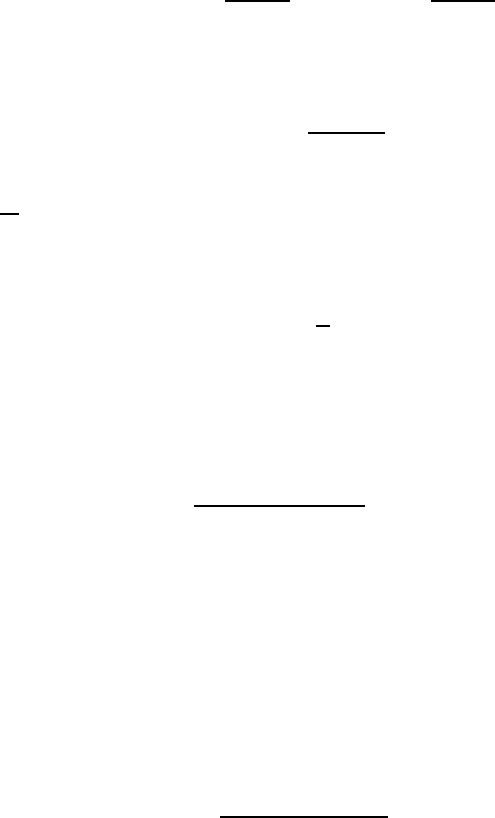
Тут k

i k

–додатнiсталiiE(|W |) < ∞.Покажiть,щоd –байєсiв-

ська оцiнка тодi i тiльки тодi, коли виконанi спiввiдношення

P(W ≤ d) ≥

+ k

, P(W ≥ d) ≥

+ k

8. Нехай X

,...,X

– повторна вибiрка з розподiлу Бернуллi з невi-

домим параметром W i потрiбно оцiнити значення W при функцiї

втрат

L(ω,d)=

(ω −d)

ω(1 − ω)

Покажiть, що якщо апрiорний розподiл W є рiвномiрним на iнтерва-

лi (0,1), то байєсiвська оцiнка δ

∗

задається рiвнiстю δ

∗

,...,X

X iбайєсiвськийризикдорiвнює1/n.

9. Нехай X

,...,X

– повторна вибiрка з експоненцiйного розподiлу з

невiдомим параметром W ,якийоцiнюєтьсяприфункцiївтрат

L(ω,d)=



− d



Нехай апрiорний розподiл для W є гамма-розподiлом з параметрами

α i β, α>2. (а) Для фiксованого числа спостережень n знайдiть

байєсiвську вирiшуючу функцiю i пiдрахуйте байєсiвський ризик.

(б) Покажiть, що якщо цiна одного спостереження дорiвнює c,то

оптимальним числом спостережень буде

n =

[c(α − 1)(α − 2)]

1/2

− (α − 1).

10. Нехай випадковий вектор X =(X

,...,X

) має мультиномiнальний

розподiл з пaраметрами n i W =(W

,...,W

) i необхiдно оцiнити

значення W при функцiї втрат

L(w,d)=



i=1

− d

)

Припустимо, що апрiорний розподiл W є розподiлом Дiрiхле з пара-

метричним вектором α =(α

,...,α

). Знайдiть байєсiвську оцiнку i

покажiть, що значення Байєсiвського ризику є

−



i=1

(α

+1)(α

+ n)

де α



i=1

236

11. Нехай X

,...,X

– повторна вибiрка з нормального розподiлу з не-

вiдомим середнiм M та мiрою точностi R. Нехай потрiбно оцiнити

значення M,причомуприM = m, R = r i значеннi оцiнки d,втрати

дорiвнюють

L(m,r,d)=(m − d)

Припустимо, що апрiорний сумiсний розподiл M i R є нормальний–

гамма розподiл з α>1. Для заданого числа спостережень n знайдiть

байєсiвську вирiшальну функцiю i покажiть, що байєсiвський ризик

дорiвнює β/[(α − 1)(τ + n)].

12. Нехай X

,...,X

– повторна вибiрка з розподiлу Бернуллi з невiдо-

мим значенням параметра W . Припустимо, що апрiорний розподiл

W такий, що P (W =1/2) = p>0, а ймовiрнiсть 1 − p рiвномiрно

розподiлена на iнтервалi 0 <W <1. Знайдiть апостерiорну ймо-

вiрнiсть того, що P (W =1/2) при



i=1

= y,iпокажiть,щоця

апостерiорна ймовiрнiсть бiльша апрiорної ймовiрностi p тодiiтiль-

ки тодi, коли має мiсце нерiвнiсть







n +1

237

Роздiл VI

Динамiчне програмування

Today is the ﬁrst day of the rest of your life.

6.1. МЕТОД РЕКУРЕНТНИХ СПIВВIДНОШЕНЬ.

ПРИНЦИП ОПТИМАЛЬНОСТI

У попереднiх роздiлах розглядались методи розв’язування задач матема-

тичного програмування, реалiзацiя яких приводила до знаходження всiх

компонент оптимального плану одночасно на останньому кроцi алгоритму.

Знайдений оптимальний план вважався дiйсним для всього перiоду фун-

кцiонування реальної системи. Отже, рiшення про оптимiзацiю роботи

системи за допомогою вибору значень її керованих параметрiв приймає-

ться один раз. У цьому випадку говорять про однокроковий (одноетапний)

процес прийняття рiшення. Природно, таке рiшення не може врахувати

можливi змiни оптимального плану в часi протягом перiоду.

Динамiчне програмування дає досить ефективний метод послiдовного прийня-

ття рiшень про оптимiзацiю роботи системи за допомогою розв’язування

серiї зв’язаних мiж собою однокрокових задач. Тодi говорять про бага-

токроковий процес прийняття рiшення чи розв’язування задачi. Це дає

можливiсть у рядi випадкiв оптимiзувати динамiчнi системи, для яких

час вiдiграє iстотну роль.

Природно, метод динамiчного програмування не є унiверсальним. Для

його застосування до конкретної задачi остання повинна мати вiдповiдну

структуру.

Метод рекурентних спiввiдношень реалiзується в обчислювальних ал-

горитмах, дiю яких буде продемонстровано на прикладi задач такого типу

z =



i=1

) → max ,



i=1

≤ b,

≥ 0,i=1,...,n,

(6.1.1)

причому можна додатково вважати всi x

≥ 0,i =1,...,n цiлочисель-

ними. Припустимо, що всi x

≥ 0,i =1,...,n, b ≥ 0, b ≥ 0, прийма-

ють цiлочисельнi значення. Отже, маємо цiлочисельну нелiнiйну зада-

чу з сепарабельними функцiями i одним обмеженням. Замiною змiнних

238



= a

,i=1,...,n задачу легко звести до спрощеного вигляду

z = z



i=1

) → max ,



i=1

≤ b,

≥ 0,i=1,...,n.

(6.1.2)

Застосуємо метод рекурентних спiввiдношень до розв’язування цiєї задачi.

Припустимо, що змiнна x

зафiксована. Тодi замiсть задачi (6.1.2) можна

розв’язувати таку задачу

n−1

= z

− f

n−1



i=1

) → max ,

n−1



i=1

≤ b − x

= b

n−1

≥ 0,

≥ 0,i=1,...,n− 1.

(6.1.3)

Структура (n − 1)-вимiрної задачi (6.1.3) аналогiчна структурi початкової

задачi (6.1.2). Проте оптимальний план останньої задачi залежить вiд зна-

чення змiнної x

, яка може набувати цiлих значень, що лежать в iнтервалi

[0,b]. Розглянемо задачу

n−1

)= Λ

n−1

(b − x

)=max

n−1



i=1

)

n−1



i=1

≤ b − x

= b

n−1

≥ 0,

≥ 0,i=1,...,n− 1.

(6.1.4)

Знайшовши функцiю Λ

n−1

(b − x

), задачу (6.1.2) можна записати так:

= f

)+Λ

n−1

(b − x

) → max ,

0 ≤ x

≤ b.

(6.1.5)

Обєднавши (6.1.4), (6.1.5), дiстаємо рекурентну формулу

(b)= max

0≤x

≤b

)+Λ

n−1

(b − x

)] . (6.1.6)

Мiркуючи аналогiчно для Λ

n−1

)=Λ

n−1

(b − x

), можемо записати

n−1

(b − x

)= max

0≤x

n−1

≤b

n−1

)+Λ

n−2

n−1

− x

n−1

)] (6.1.7)

i, нарештi, для k-го кроку

)= max

0≤x

≤b

)+Λ

k−1

− x

)] , (6.1.8)

239

де

k−1

)= Λ

k−1

− x

)= max

,...,x

k−1



i=1

)

k−1



i=1

≤ b

k−1

= b

− x

= b −



i=k

≥ 0,i=1,...,k− 1.

(6.1.9)

При k =1матимемо

)= max

0≤x

≤b

)] ,

= b −



i=2

(6.1.10)

Для реалiзацiї обчислювального алгоритму слiд застосувати описанi про-

цедури у зворотному порядку: спочатку розв’язати задачу (6.1.10) для

всiх b

=0,1,2,...,b. Потiм, користуючись рекурентними спiввiдношен-

нями (6.1.9), обчислити функцiї Λ

),k =2,3,...,n для всiх можливих

значень b

. Остання з них Λ

) буде рiвною оптимальному значенню

z = z

∗

. Отже, процес обчислень насправдi полягає в табулюваннi функцiй

),k =1,2,...,n, i вiдповiдних їм значень змiнних

ˆx

=ˆx

)=ˆx

(b −



i=k+1

ˆx

). (6.1.11)

Продемонструємо дiю методу на конкрктному прикладi.

Приклад 6.1.1. Розв’яжемо задачу

z =2x

− x

+ x

→ max ,

+ x

+3x

≤ 6.

≥ 0,i =1,2,3.

Перепишемо задачу у виглядi

z =

− x

→ max ,

+ x

≤ 6.

≥ 0,i =1,2,3.

1-й крок. Обчислимо

)= max

0≤x

≤b

2-й крок. Скористаємось формулою (6.1.8) для k =2iзнайдемо

)= max

0≤x

≤b

−x

+Λ

− x

)

(

=max

0≤x

≤b

[Ω

)] .

Величини Λ

) знаходять, порiвнюючи мiж собою значення Ω

обчисленi для кожного b

=0,1,...,6 та всiх x

=0,...,b

.Наприклад,

240