Моклячук М.П., Ямненко Р.Є. Лекції з теорії вибору та прийняття рішень (на укр. языке)
Подождите немного. Документ загружается.

Для кожного значення w ∈ Ω через ризик ρ (w,δ) ми будемо позначати
ризик, що вiдповiдає вирiшуючiй функцiї
δ при W = w:
ρ (w,δ)=
S
L [w,δ (x)] f ( x|w) dµ (x). (3.6.3)
Для кожної вирiшуючої функцiї
δ ∈ ∆ функцiя ρ (·,δ),якавизначена
формулою (3.6.3), називається її функцiєю ризику. З (3.6.1) i (3.6.3)
випливає, що
ρ (p,δ)=
Ω
ρ (w,δ) p (w) dν (w). (3.6.4)
Нехай
δ
∗
∈ ∆ –такавирiшуючафункцiя,що
ρ (p,δ
∗
)= inf
δ∈ ∆
ρ (p,δ)=ρ
∗
(p) . (3.6.5)
Тодi
δ
∗
називається байєсiвською вирiшуючою функцiєю при розподiлi
ймовiрностей
p,аρ
∗
(p) як i ранiше називається байєсiвським ризиком.
Для кожного розподiлу ймовiрностей
p параметра W статистику варто
вибирати вирiшуючу функцiю
δ, що є байєсiвською вирiшуючою фун-
кцiєю при розподiлi
p.
3.7. ПОБУДОВА БАЙЄСIВСКИХ ВИРIШУЮЧИХ
ФУНКЦIЙ
Нехай для розподiлу ймовiрностей p параметра W потрiбно знайти
вирiшуючу функцiю
δ, яка мiнiмiзує значення ризику ρ (p,δ),щозада-
ється формулою (3.6.1). Ми будемо припускати, що в цьому спiввiдно-
шеннi можна змiнити порядок iнтегрування. Зокрема, ця перестановка
законна для всiх розподiлiв ймовiрностей
p iвсiхвирiшуючихфункцiй
δ, якщо функцiя втрат L невiд’ємна та обмежена. Пiсля зазначеної змiни
порядку iнтегрування ризик
ρ (p,δ) приймає вигляд
ρ (p,δ)=
S
Ω
L [w,δ (x) f ( x|w) p (w) dν (w)]
dµ (x). (3.7.1)
Вирiшуючу функцiю
δ, яка мiнiмiзує цей ризик, можна визначити з умо-
ви мiнiмiзацiї, при кожному значеннi
x ∈ S, внутрiшнього iнтеграла в
(3.7.1). Iншими словами, байєсiвську вирiшуючу функцiю
δ
∗
при роз-
подiлi ймовiрностей
p можна одержати наступним чином: для кожного
значення
x ∈ S приймаємо δ
∗
(x)=d
∗
,деd
∗
– рiшення з D, яке мiнiмiзує
iнтеграл
Ω
L (w,d) f ( x|w) p (w) dν (w). (3.7.2)
191

Цей результат допускає таку iнтерпретацiю. Для усiх x ∈ S покладемо
f
1
(x)=
Ω
f ( x|w) p (w) dν (w). (3.7.3)
Оскiльки
f
1
(x) є щiльнiстю розподiлу ймовiрностей для X,тоf
1
(x)
може дорiвнювати нулю лише на множинi точок x,щомаютьнульо-
ву ймовiрнiсть. Замiсть того щоб шукати рiшення
d
∗
,щодаємiнiмум
iнтегралу (3.7.2), статистик може визначити значення
d
∗
, яке мiнiмiзує
iнтеграл
Ω
L (w,d)
#
f ( x|w) p (w)
f
1
(x)
$
dν (w) .
(3.7.4)
Дрiб у квадратних дужках в iнтегралi (3.7.4) є умовною щiльнi-
стю розподiлу ймовiрностей випадкової величини
W при X = x,то-
му значення iнтеграла дорiвнює умовному математичному сподiванню
E
[L (W,d)|x]. Отже, рiшення d
∗
, яке мiнiмiзує iнтеграл (3.7.2), є по-
просту те, якому вiдповiдає найменший середнiй збиток при умовному
розподiлi
W , коли спостереженим значенням X виявилося x. Iншими
словами,
d
∗
– байєсiвське рiшення при умовному розподiлi W при X = x.
У статистичних задачах прийняття рiшеннь початковий розподiл
W
називається апрiорним розподiлом W , тому що вiн задає розподiл W
до проведення спостереження над X. Умовний розподiл W при вiдомо-
му значеннi
X називається апостерiорним розподiлом W ,томущовiн
задає розподiл пiсля спостереження значення величини
X.
Корисно уявляти собi байєсiвську вирiшуючу функцiю наступним чи-
ном. Якщо рiшення приймається без попереднiх спостережень, то опти-
мальним є байєсiвське рiшення при апрiорному розподiлi
W .Якщожпе-
ред прийняттям рiшення спостерiгається значення
X, то задача прийня-
ття рiшення для статистика, власне кажучи, та ж сама, як i в першому
випадку, рiзниця лише в тому, що апрiорний розподiл
W замiнився на
апостерiорний. Отже, тепер оптимальним є байєсiвське рiшення при апо-
стерiорному розподiлi
W .
З цих мiркувань ясно, що рiшення
δ
∗
(x
0
),щозадаєтьсябайєсiв-
ською вирiшуючою функцiєю
δ
∗
для певного значення x
0
,щоєрезульта-
том спостереження, можна знайти i без того, щоб обчислювати рiшення
δ
∗
(x) для всiх значень x. Байєсiвську вирiшуючу функцiю δ
∗
для роз-
подiлу ймовiрностей
p можна знаходити i без обчислення байєсiвського
ризику
ρ
∗
(p).
Приклад 3.7.1. Як iлюстрацiю отриманих результатiв розглянемо за-
дачу, в якiй
Ω={w
1
,w
2
}, D = {d
1
,d
2
},афункцiявтратL задається
таблицею 3.7.1.
Табл.3.7.1
192

d
1
d
2
w
1
0 5
w
2
10 0
Припустимо, що статистик може спостерiгати випадкову величину X з
такими умовними розподiлами:
P
(X =1|W = w
1
)=
3
4
, P ( X =0|W = w
1
)=
1
4
,
P ( X =1|W = w
2
)=
1
3
, P ( X =0|W = w
2
)=
2
3
.
(3.7.5)
Потрiбно побудувати байєсiвську вирiшуючу функцiю за умови, що апрi-
орний розподiл параметра
W такий:
P
(W = w
1
)=p, P (W = w
2
)=1− p, (3.7.6)
де
p –заданечисло,0 ≤ p ≤ 1.
Для
x ∈{0,1} нехай p (x) позначає апостерiорну ймовiрнiсть подiї
W = w
1
, якщо спостерiгалось значення x величини X ,тобто
p (x)=P (W = w
1
|X = x) . (3.7.7)
ЗформулиБайєса
p(x)=P ( W = w
1
|X = x)= (3.7.8)
=
P ( X = x|W = w
1
) P (W = w
1
)
P ( X = x|W = w
1
) P (W = w
1
)+P ( X = x|W = w
2
) P (W = w
2
)
i рiвностей (3.7.5), (3.7.6) випливає, що
p (1) =
3
4
p
3
4
p +
1
3
(1 − p)
,p(0) =
1
4
p
1
4
p +
2
3
(1 − p)
.
(3.7.9)
Пiсля спостереження значення
x величини X треба вибрати одне з рi-
шень
d
1
чи d
2
. З таблицi 3.7.1 видно, що ризик вiд прийняття рiшення d
1
дорiвнює 10(1 − p (x)), а ризик вiд прийняття d
2
дорiвнює 5p (x).Отже,
d
2
є байєсiвським рiшенням, якщо p (x) <
2
3
; d
1
є байєсiвським рiшен-
ням, якщо
p (x) >
2
3
,аувипадкуp (x)=
2
3
як d
1
так i d
2
–байєсiвськi
рiшення. Звiдси i з вигляду апостерiорних ймовiрностей (3.7.9) виплива-
ють наступнi результати.
Якщо спостерiгається значення
X =1,тодлябайєсiвськоївирiшую-
чої функцiї
δ
∗
маємо: δ
∗
(1) = d
2
за умови, що p (1) <
2
3
чи, що теж саме,
за умови, що
p<
8
17
; δ
∗
(1) = d
1
при p>
8
17
;нарештi,приp =
8
17
обидва
рiшення
d
1
i d
2
єбайєсiвськими.Отже
δ
∗
(1) =
d
2
, 0 ≤ p ≤
8
17
,
d
1
,
8
17
≤ p ≤ 1.
(3.7.10)
Якщо ж спостерiгається значення
X =0,то:δ
∗
(0) = d
2
при p (0) <
2
3
,
тобто при
p<
16
19
;далi,δ
∗
(0) = d
1
при p>
16
19
;нарештi,приp =
16
19
обидва
193
рiшення d
1
i d
2
єбайєсiвськими.Отже
δ
∗
(0) =
d
2
, 0 ≤ p ≤
16
19
,
d
1
,
16
19
≤ p ≤ 1.
(3.7.11)
Обчислимо тепер значення байєсiвського ризику
ρ
∗
(p) для довiльної
апрiорної ймовiрностi
p.
1. Якщо
0 ≤ p ≤
8
17
, то рiшення d
2
буде байєсiвським незалежно вiд
того, яке значення
X спостерiгається. Отже вiдповiдно до таблицi
3.7.1, для таких
p маємо ρ
∗
(p)=5p.
2. Якщо
8
17
<p<
16
19
,тоδ
∗
(0) = d
2
i δ
∗
(1) = d
1
. Тому з рiвностей
(3.6.5) i таблицi 3.7.1 видно, що
ρ
∗
(p)=pρ(w
1
,δ
∗
)+(1−p) ρ (w
2
,δ
∗
)=
= p
'
0 ·
3
4
+5·
1
4
(
+(1−p)
'
10 ·
1
3
+0·
2
3
(
=
=
5
4
p +
10
3
(1 − p) .
3. Якщо
16
19
≤ p ≤ 1, то рiшення d
1
буде байєсiвським незалежно вiд
того, яке значення
X спостерiгається. Вiдповiдно до таблицi 3.7.1,
уцьомувипадку
ρ
∗
(p)=10(1− p).
Отже,
ρ
∗
(p)=
5p, 0 ≤ p ≤
8
17
,
5
4
p +
10
3
(1 − p) ,
8
17
≤ p ≤
16
17
,
10 (1 − p) ,
16
17
<p≤ 1.
(3.7.12)
Графiк байєсiвського ризику
ρ
∗
(p) поданий на рис. 3.7.1.
3.8. ЦIНА СПОСТЕРЕЖЕННЯ
У багатьох статистичних задачах прийняття рiшень спостереження
випадкової величини
X пов’язано з певними витратами, якi мають вра-
ховуватися статистиком при розрахунку ризику вiд прийняття рiшень,
що використовує результати спостереження
X. Ця обставина грає осо-
бливо важливу роль у випадку, коли статистику треба вирiшити, яку
з декiлькох випадкових величин спостерiгати, або вирiшити, чи роби-
ти спостереження взагалi. Нехай
c (w,x) позначає цiну спостереження
значення
x величини X,якщоW = w.Тодi,якщоp –церозподiл
ймовiрностей випадкової величини
W , то середня цiна спостереження
дорiвнює
E
[c (W,X )] =
Ω
S
c (w,x) f ( x|w) p (w) dµ (x) dν (w).
194
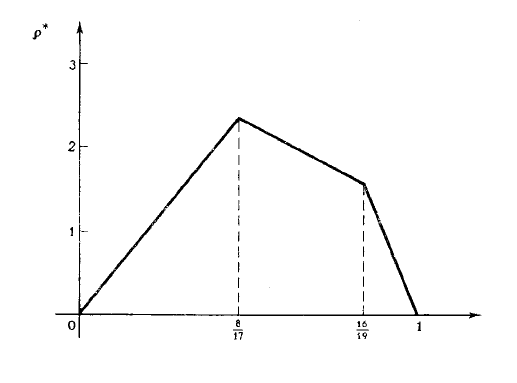
Рис. 3.7.1: Графiк байєсiвського ризику.
Ми будемо припускати, що для цiни c (W,X) є вiрним припущення
про середню кориснiсть. Iншими словами, будемо вважати, що ця цiна
виражена у вiдповiдних одиницях вiд’ємної корисностi так, що iстотним
для нас є лише середнє значення ймовiрнiсного розподiлу цiни
c (W,X ).
Загальним ризиком вiд спостереження
X i прийняття вирiшуючої
функцiї
δ називається сума ризику ρ (p,δ) i середньої цiни спостереже-
ння E
[c (W,X )]. Статистик має вибрати спостереження з деякого класу
доступних спостереженню випадкових величин i вiдповiдну байєсiвську
вирiшуючу функцiю
δ, яка мiнiмiзує загальний ризик.
Виражаючи загальний ризик у виглядi суми ризику вирiшуючої фун-
кцiї
δ i середньої цiни спостереження, ми неявно використовуємо при-
пущення про адитивнiсть корисностей статистика. Власне кажучи, всi
результати в теорiї статистичних рiшень ґрунтуються на цьому припу-
щеннi, i ми будемо використовувати його далi.
Дуже часто статистик може вибрати той чи iнший об’єм випадкової
вибiрки i цiна спостереження залежить лише вiд цього об’єму вибiрки.
Iншими словами, цiна спостереження не залежить вiд
W чи вiд значень
випадкової величини
X.
Приклад 3.8.1. Розглянемо знову приклад 3.7.1 i припустимо тепер, що
цiна спостереження випадкової величини
X дорiвнює c, c>0.Стати-
стик може прийняти рiшення, не спостерiгаючи
X,абозаплатитисуму
195
c iспостерiгатиX перед прийняттям рiшення. При заданому апрiорно-
му розподiлi
p ставиться питання, на яку суму c варто погоджуватися
статистику?
Для розв’язання цiєї задачi треба порiвняти мiнiмальне значення ри-
зику
ρ
∗
(p) без врахування цiни спостереження c,якеможнаотримати
на основi спостереження
X, з мiнiмальним ризиком ρ
0
(p),щовiдпо-
вiдає байєсiвському рiшенню при вiдсутностi спостережень. Функцiя
ρ
∗
вже знайдена. Графiк функцiї зображений на рисунку 3.7.1. Функцiя ρ
0
,
згiдно таблицi 3.7.1, має вигляд
ρ
0
(p)=
5p, 0 ≤ p ≤
2
3
,
10 (1 − p) ,
2
3
<p≤ 1.
(3.8.1)
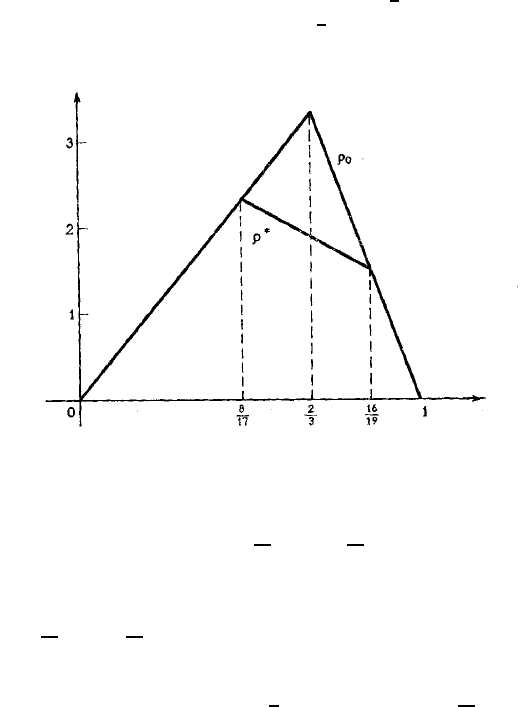
Графiки функцiй
ρ
∗
i ρ
0
зображенi на рисунку 3.8.1. З цього рисунка
Рис. 3.8.1: Графiки ризику ρ
∗
(p) та ρ
0
(p).
видно, що ρ
∗
(p)=ρ
0
(p),якщоp ≤
8
17
чи p ≥
16
19
.
Отже, при значеннi апрiорної ймовiрностi
p,щолежитьводномуз
цих iнтервалiв, статистик може досягти i без спостереження
X того ж
значення ризику, що i при спостереженнi
X.
Якщо ж
8
17
<p<
16
19
,тоρ
∗
(p) <ρ
0
(p). За можливiсть спостереження
величини
X перед прийняттям рiшення статистику варто погоджуватися
на будь-яку цiну
c таку, що c<[ρ
0
(p) − ρ
∗
(p)]. Рiзниця мiж ризиками
[ρ
0
(p) − ρ
∗
(p)] максимальна для p =
2
3
,девонадорiвнює
25
18
.
196

Приклад 3.8.2. Припустимо тепер, що в задачi прийняття рiшень з
прикладу 3.7.1 статистик може вибирати число спостережень випадкової
величини
X. Iншими словами, статистик може спостерiгати значення n
випадкових величин X
1
,...,X
n
, причому при кожному фiксованому зна-
ченнi
W = w
i
,i =1,2, величини X
1
,...,X
n
незалежнi й однаково розподi-
ленi з тим же умовним розподiлом
f ( ·|w
i
), що й одне спостереження X
з прикладу 3.7.1. Умовнi розподiли f ( ·|w
i
) задаються рiвностями (3.7.5)
i можуть бути записанi в такому виглядi (при
x =0,1)
f ( x|w
1
)=
3
x
4
,f(x|w
2
)=
2
1−x
3
.
(3.8.2)
Для будь-якої послiдовностi результатiв
x
1
,...,x
n
спостережень X
1
,...,
X
n
покладемо y =
n
i=1
x
i
. Тодi значення g ( x
1
,...,x
n
|w
i
) умовного розпо-
дiлу випадкових величин
X
1
,...,X
n
за умови W = w
i
такi:
g ( x
1
,...,x
n
|w
1
)=
3
y
4
n
,g( x
1
,...,x
n
|w
2
)=
2
n−y
3
n
. (3.8.3)
Якщо цiна кожного спостереження дорiвнює
c>0,товибiркуякого
об’єму
n варто обрати статистику?
Для будь-якої апрiорної ймовiрностi
p = P (W = w
1
) позначимо через
p (x
1
,...,x
n
) апостерiорну ймовiрнiсть того, що W = w
1
,заумови,що
зроблено вибiрку обсягу
n i X
1
= x
1
,...,X
n
= x
n
.ЗтеоремиБайєса
випливає, що
p (x
1
,...,x
n
)=
3
y
4
n
p
3
y
4
n
p +
2
n−y
3
n
(1 − p)
=
=
#
1+
1 − p
p
8
3
n
1
6
y
$
−1
. (3.8.4)
Як було показано в прикладi 3.7.1, при
p (x
1
,...,x
n
) <
2
3
рiшення d
2
є
байєсiвським, у протилежному випадку
d
1
– байєсiвське рiшення. Тому з
(3.8.4) видно, що байєсiвська вирiшуюча функцiя
δ
n
(x
1
,...,x
n
) приймає
значення
d
2
,якщо
y<
log[2(1− p) /p]+n log
8
3
log 6
(3.8.5)
У протилежному випадку
δ
n
(x
1
,...,x
n
) приймає значення d
1
.
Нехай
k
n
позначає значення правої частини нерiвностi (3.8.5). З та-
блицi 3.7.1 видно, що ризик
ρ (p,δ
n
) байєсiвськой вирiшуючої функцiї δ
n
197

задовольняє спiввiдношенню
ρ (p,δ
n
)=5p P
n
i=1
X
i
<k
n
W = w
1
+
+10 (1 − p)
P
n
i=1
X
i
≥ k
n
W = w
2
.
(3.8.6)
Умовний розподiл суми
n
i=1
X
i
при W = w
1
є бiномiальним з параметрами
n i
3
4
. Умовний розподiл суми
n
i=1
X
i
утомувипадку,колиW = w
2
та-
кож бiномiальний, але з параметрами
n i
1
3
.Отже,ризикρ (p,δ
n
) можна
обчислити для будь-якої апрiорної ймовiрностi
p iнезанадтовеликого
обсягу вибiрки
n за таблицями бiномiального розподiлу. Для великих
значень
n значення ρ (p,δ
n
) можна обчислити, використовуючи нормаль-
ну апроксимацiю бiномiального закону (теорема Муавра-Лапласа) i та-
блицi нормального розподiлу.
Для одержання загального ризику байєсiвської вирiшуючої функцiї
δ
n
(x
1
,...,x
n
) при вибiрцi обсягу n до ризику ρ (p,δ
n
) потрiбно додати
цiну вибiрки
nc. Оптимальний об’єм вибiрки при апрiорнiй ймовiрностi p
– це значення n, яке мiнiмiзує загальний ризик ρ
t
(p,δ
n
), що визначається
формулою
ρ
t
(p,δ
n
)=ρ (p,δ
n
)+nc. (3.8.7)
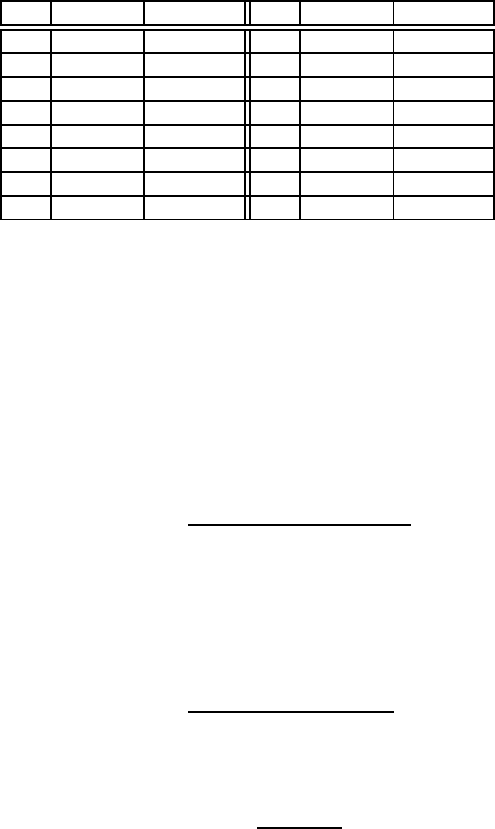
У таблицi 3.8.1 наведенi деякi значення ризику
ρ (p,δ
n
) i загального
ризику
ρ
t
(p,δ
n
) при апрiорнiй ймовiрностi p =
2
3
, i цiнi спостереження
c =0,01. Слiд зазначити, що ризик ρ (p,δ
n
) обов’язково спадає з ростом n.
Однак, через те що спостереження мають дискретний розподiл, загаль-
ний ризик
ρ
t
(p,δ
n
) як функцiя вiд n може мати незначнi коливання (на
фонi загальної картини). З таблицi 3.8.1 видно, що оптимальний обсяг
вибiрки в нашiй задачi дорiвнює 25, а мiнiмальне значення загального
ризику дорiвнює 0,3403.
Табл.3.8.1
198
n ρ (p,δ
n
) ρ
t
(p,δ
n
) n ρ (p,δ
n
) ρ
t
(p,δ
n
)
21 0.1394 0.3494 29 0.0609 0.3509
22 0.1370 0.3570 30 0.0513 0.3513
23 0.1116 0.3416 31 0.0506 0.3606
24 0.1056 0.3456 32 0.0411 0.3611
25 0.0903 0.3403 33 0.0402 0.3702
26 0.0822 0.3422 34 0.0334 0.3734
27 0.0738 0.3438 35 0.0313 0.3813
28 0.0646 0.3446
3.9. ОБЧИСЛЕННЯ АПОСТЕРIОРНОГО РОЗПОДIЛУ У
ТОМУ ВИПАДКУ, КОЛИ СПОСТЕРЕЖЕННЯ
ВIДБУВАЮТЬСЯ В КIЛЬКА ЕТАПIВ
Розглянемо тепер задачу, у якiй спостерiгаються двi випадковi вели-
чини (чи два випадкових вектори)
X та Y .Нехайf (x,y|w) є сумiсний
умовний розподiл ймовiрностей
X та Y при W = w, w ∈ Ω.Апостерiор-
ний розподiл
p (w|x,y) параметра W при X = x та Y = y обчислюється
вточцi
w за формулою
p (w|x,y)=
f ( x,y|w) p (w)
Ω
f ( x,y|w
) p (w
) dν (w
)
.
(3.9.1)
Припустимо, що
X та Y спостерiгаються не одночасно, X спостерiгає-
ться ранiше вiд
Y .Нехайg ( x|w) позначає умовний розподiл ймовiрно-
стей
X при W = w. Пiсля спостереження X = x ми можемо обчислити
апостерiорний розподiл
p (w|x) для W перед спостереженням Y за фор-
мулою
p (w|x)=
g ( x|w) p (w)
Ω
g ( x|w
) p (w
) dν (w
)
.
(3.9.2)
Далi, умовний розподiл ймовiрностей
h (y|w,x) для Y при W = w i
X = x має вигляд
h (y|w,x)=
f (x,y|w)
g (x|w)
.
(3.9.3)
Отже, на другому етапi експерименту, коли спостерiгається
Y ,розпо-
дiл ймовiрностей (3.9.2) можна розглядати як апрiорний розподiл ймо-
вiрностей для
W , i умовнi розподiли ймовiрностей (3.9.3) утворюють при
w ∈ Ω вiдповiдне сiмейство розподiлiв Y . Апостерiорний розподiл ймо-
вiрностей
ξ ( ·|x,y) параметра W при Y = y можна знайти наступним
199

чином:
p (w|x,y)=
h (y|w,x) p ( w|x)
Ω
h (y|w
,x) p ( w
|x) dν (w
)
.
(3.9.4)
Якщо розподiли ймовiрностей (3.9.2) i (3.9.3) пiдставити в (3.9.4),
то прийдемо до (3.9.1). Це означає, що якщо спостереження проводя-
ться в декiлька етапiв, то апостерiорний розподiл можна обчислювати
на кожному етапi, беручи як апрiорний розподiл для наступного етапу
апостерiорний розподiл, отриманий на попередньому етапi. З наших мiр-
кувань також випливає, що якщо апостерiорний розподiл
W при X = x
та Y = y обчислюється в два прийоми, то остаточний результат не за-
лежить вiд того, яка з випадкових величин,
X чи Y ,спостерiгалася
спочатку.
Процес прийняття рiшення може бути тепер описаний у такому спро-
щеному виглядi. В заданий момент часу статистик має розподiли ймо-
вiрностей параметра
W . З часом до статистика надходить iнформацiя
про
W , i статистик використовує цю iнформацiю для переоцiнки розпо-
дiлу
W . У тi моменти часу, коли статистику треба прийняти рiшення,
наслiдки якого пов’язанi з
W , вiн вибирає рiшення, оптимальне щодо
розподiлу
W в даний момент.
Такий процес прийняття рiшень досить реалiстичний. Дiйсно, про-
тягом життя ми переглядаємо нашi уявлення про параметри з ростом
iнформацiї про них i, приймаючи рiшення, ґрунтуємося на наших сьо-
годнiшнiх уявленнях. У деяких ситуацiях, однак, вiд вибору рiшення в
даний момент може залежати та iнформацiя, яку ми одержимо надалi, i
отже, цей вибiр може вплинути на рiшення статистика, якi вiн прийме
в майбутньому. Задачi, у яких статистик повинен брати до уваги май-
бутнє i будувати вiдповiднi плани, називаються задачами послiдовного
прийняття рiшень.
3.9.1. Задачi для самостiйної роботи
1. Розглянемо задачу прийняття рiшень, у якiй Ω={w
1
,w
2
}, D =
{d
1
,d
2
,d
3
} iфункцiявтратL(w,d) задається таблицею нижче. Пока-
жiть, що d
3
є байєсiвським рiшенням при заданому розподiлi пара-
метра W тодi i лише тодi, коли
1
3
≤ P (W = w
1
) ≤
5
9
.
2. Розглянемо задачу прийняття рiшень, у якiй параметричний простiр
Ω складається з усiх чисел w iнтервалу 0 ≤ w ≤ 1, простiр рiшень
D –цевсiдiйснiчислаR
1
iдляусiхw ∈ Ω i d ∈ D функцiя втрат
200
