Моклячук М.П., Ямненко Р.Є. Лекції з теорії вибору та прийняття рішень (на укр. языке)
Подождите немного. Документ загружается.


шкою. Вибiр другого гравця (покласти монету вверх гербом чи решкою)
залежить тепер вiд того, який вибiр зробив перший гравець. Позначи-
мо через 1 вибiр герба, а через 2 – вибiр решки. Позначимо через
(i,j)
стратегiю другого гравця, яка полягає в тому, що гравець вибирає i,ко-
ли перший гравець вибирає 1 (герб), i вибирає
j,колипершийгравець
вибирає 2 (решка).
H
H
H
H
H
H
H
H
@
@
@
@
@
@
@
@
@
@
(−1,1)(1,−1)(1,−1)(−1,1)
1
22
РГРГ
ГР
Рис. 2.10.2: Приклад 2.10.1 б)
Дерево гри зображено на рис. 2.10.2. У першого гравця iнформацiйна
множина складається з однiєї точки (початкова позицiя гри). Ця точка
обведена колом. У другого гравця двi iнформацiйних множини. Кожна
мiстить одну точку (обведенi колом).
Нормальна форма гри задається таблицею 2.10.2. Числа в таблицi вка-
зують на виграш першого гравця.
Табл.2.10.2
(1,1) (1,2) (2,1) (2,2)
1 −1 −1 1 1
2 1 −1 1 −1
Приклад 2.10.2. У грi беруть участь два гравцi. Гравець P
1
робить
перший хiд. Вiн вибирає число
x iз множини чисел {1,2}.ГравецьP
2
робить другий хiд. Вiн вибирає число y iз множини чисел {1,2}. Третiй
хiд робить гравець
P
1
.Вiнвибираєчислоz iз множини чисел {1,2}.
В кiнцi гри гравець
P
2
платить гравцю P
1
суму M(x,y,z),дефункцiя
M(x,y,z) приймає такi значення:
M(1,1,1) = −2, M (1,1,2) = −1, M (1,2,1) = 3, M (1,2,2) = −4,
161
M(2,1,1) = 5, M(2,1,2) = 2, M (2,2,1) = 2, M (2,2,2) = 6.
Iнформацiя, яку мають гравцi:
а) гравець
P
1
знає x та y;гравецьP
2
знає x;
б) гравець
P
1
знає x,аленезнаєy;гравецьP
2
знає x.
Зобразити гру у виглядi топологiчного дерева. Описати всi стратегiї грав-
цiв. Знайти нормальну форму гри.
У першому варiантi гри гравець
P
2
має чотири стратегiї. Їх стiльки,
скiльки є способiв вiдображення множини
{1,2} (кiлькостi iнформацiй-
них множин гравця) у множину
{1,2} (кiлькiсть альтернатив для кожної
iнформацiйної множини). Якщо ми позначимо через
f
ij
(x) таку функцiю,
що
f
ij
(1) = i, f
ij
(2) = j, то чотири стратегiї гравця P
2
–цефункцiїf
11
,
f
12
, f
21
, f
22
.
H
H
H
H
H
H
H
H
@
@
@
@
@
@
@
@
@
@
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
−2 − 1 3 −4 5226
21212121
1111
2121
1
2
1
2
2
Рис. 2.10.3: Приклад 2.10.2 а)
Стратегiя гравця P
1
повинна вказувати йому, який вибiр робити пiд
час першого та третього ходу. Перший хiд буде зроблений, якщо вибрати
1 або 2. Перед третiм ходом гравець повинен визначити вибiр
z для всiх
значень
x, y. Стратегiї гравця P
1
можна записати у виглядi
i
0
i
11
i
12
i
21
i
22
,
де i
0
вказує на число (1 або 2), яке гравець вибирає пiд час першого ходу,
а
i
jk
– число, яке вiн вибирає пiд час третього ходу в тому випадку, коли
число
j було вибрано пiд час першого ходу i число k було вибрано пiд
162
час другого ходу. Якщо гравець P
1
застосовує, наприклад, стратегiю
1 2121,
то це означає, що P
1
вибирає 1 пiд час першого ходу; якщо пiд час
першого ходу була вибрана 1 i пiд час другого ходу гравець
P
2
вибрав 1,
то
P
1
вибирає 2 пiд час третього ходу. Всього у гравця P
1
32 стратегiї.
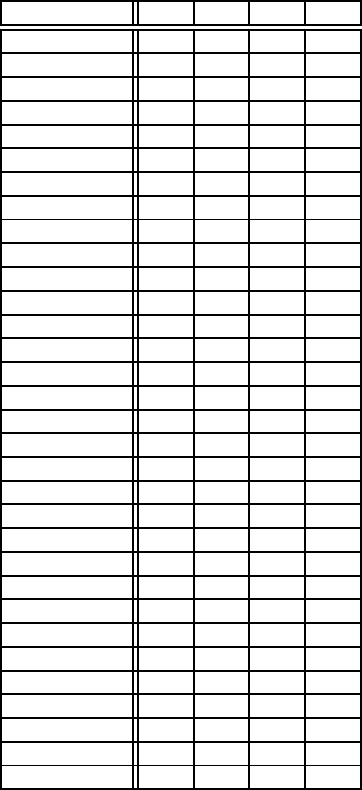
Дерево гри зображено на рис. 2.10.3. Нормальна форма гри задається
таблицею 2.10.3. Ця матриця має сiдловi точки. Цiна гри дорiвнює 5.
Табл.2.10.3
163
f
11
f
12
f
21
f
22
1 1111 −2 −2 3 3
1 1112 −2 −2 3 3
1 1121 −2 −2 3 3
1 1122 −2 −2 3 3
1 1211 −2 −2 −4 −4
1 1212 −2 −2 −4 −4
1 1221 −2 −2 −4 −4
1 1222 −2 −2 −4 −4
1 2111 −1 −1 3 3
1 2112 −1 −1 3 3
1 2121 −1 −1 3 3
1 2122 −1 −1 3 3
1 2211 −1 −1 −4 −4
1 2212 −1 −1 −4 −4
1 2221 −1 −1 −4 −4
1 2222 −1 −1 −4 −4
2 1111 5 2 5 2
2 1112 5 6 5 6
2 1121 2 2 2 2
2 1122 2 6 2 6
2 1211 5 2 5 2
2 1212 5 6 5 6
2 1221 2 2 2 2
2 1222 2 6 2 6
2 2111 5 2 5 2
2 2112 5 6 5 6
2 2121 2 2 2 2
2 2122 2 6 2 6
2 2211 5 2 5 2
2 2212 5 6 5 6
2 2221 2 2 2 2
2 2222 2 6 2 6
Будь-яка iз чотирьох стратегiй
2 1112, 2 1212,
2 2112, 2 2212
єоптимальноюдлягравцяP
1
.ДлягравцяP
2
оптимальними є стратегiї
f
11
та f
12
. По вiдношенню до початкової форми гри це означає, що один
iз оптимальних способiв гри для гравця
P
1
такий: пiд час першого ходу
164

вибирати 2, а пiд час третього ходу вибирати те число, яке гравець
P
2
вибрав пiд час другого ходу. Один iз оптимальних способiв гри для
гравця
P
2
такий: пiд час другого ходу вибирати 1 незалежно вiд того,
яке число гравець
P
1
вибрав пiд час першого ходу. Iнший оптимальний
спосiб – вибирати число вiдмiнне вiд того, яке вибрав гравець
P
1
пiд час
першого ходу.
Зауваження. Кiлькiсть стратегiй гравця
P
1
може бути зменшена до 8.
Так, наприклад, якщо
P
1
вибирає 1 пiд час першого ходу, то значення
i
21
, i
22
не враховуються. Аналогiчно, якщо P
1
вибирає 2 пiд час першого
ходу, то значення
i
11
, i
12
не враховуються. Це вiдображено в таблицi
(порiвняйте рядки).
У другому варiантi гри гравець
P
2
має тi ж чотири стратегiї. Цi чоти-
ри стратегiї гравця
P
2
описуються функцiями f
11
, f
12
, f
21
, f
22
.Стратегiї
гравця
P
1
повиннi вказувати йому, який вибiр робити пiд час першого та
третього ходу. Перший хiд буде зроблений, якщо вибрати 1 або 2. Перед
третiм ходом гравець повинен визначити вибiр
z для всiх значень x, y.
Стратегiї гравця
P
1
можна записати у виглядi 11 , 12, 21, 22,
де перша цифра вказує на число (1 або 2), яке гравець вибирає пiд час
першого ходу, а друга цифра вказує на число, яке вiн вибирає пiд час
третього ходу.
Дерево гри зображено на рис. 2.10.4. Ця матриця не має сiдлових точок.
H
H
H
H
H
H
H
H
@
@
@
@
@
@
@
@
@
@
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
−2 − 1 3 −4 522 6
21212121
1111
2121
1
2
1
2
2
Рис. 2.10.4: Приклад 2.10.2 б)
165
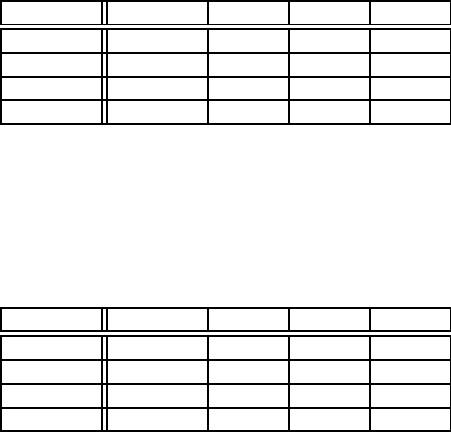
Нормальна форма гри задається таблицею 2.10.4.
Приклад 2.10.3. У грi беруть участь два гравцi. Перший хiд випадко-
вий. Випадково вибирається число
x з множини {1,2}, P {x =1} =1/2,
P {x =2} =1/2.ГравецьP
1
робить другий хiд. Вiн вибирає число y
iз множини {1,2}.ГравецьP
2
робить третiй хiд. Вiн вибирає число z iз
множини
{1,2}.ВкiнцiгригравецьP
2
платить гравцю P
1
суму M(x,y,z),
де функцiя приймає такi значення:
M(1,1,1) = −2, M(1,1,2) = 2, M(1,2,1) = −4, M (1,2,2) = 3,
M(2,1,1) = 5, M(2,1,2) = −3, M (2,2,1) = −1, M (2,2,2) = 6.
Iнформацiя, яку мають гравцi:
а) гравець
P
1
знає x;гравецьP
2
не знає x,алезнаєy;
б) гравець
P
1
знає x;гравецьP
2
знає лише x + y;
Зобразити гру у виглядi топологiчного дерева. Описати всi стратегiї грав-
цiв. Знайти нормальну форму гри.
Табл.2.10.4
f
11
f
12
f
21
f
22
11 −2 −2 3 3
12 −1 −1 −4 −4
21 5 2 5 2
22 2 6 2 6
У першому варiантi гри гравець P
1
iгравецьP
2
мають по чотири страте-
гiї. Їх стiльки, скiльки є способiв вiдображення множини
{1,2} (кiлькостi
iнформацiйних множин гравця) у множину
{1,2} (кiлькiсть альтернатив
для кожної iнформацiйної множини). Цi чотири стратегiї гравцiв є фун-
кцiї
f
11
, f
12
, f
21
, f
22
.
Табл.2.10.5
f
11
f
12
f
21
f
22
f
11
3/2 3/2 8/2 8/2
f
12
−3/2 4/2 1/2 8/2
f
21
1/2 8/2 −7/2 0
f
22
−5/2 9/2 −5/2 9/2
Гра зображена на рис. 2.10.5, де бiля початкової позицiї гри стоїть 0,
який показує, що перший хiд випадковий. Припустимо, що, наприклад,
гравець
P
1
застосовує стратегiю f
21
,агравецьP
2
застосовує стратегiю
f
12
. Тодi ми отримаємо два результати в залежностi вiд того, яким буде
результат першого випадкового ходу.
166

H
H
H
H
H
H
H
H
Q
Q
Q
Q
Q
Q
Q
Q
A
A
A
A
A
A
A
A
A
A
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
−2 2 −4 35 −3 −1 6
21212121
22
222
0
1
1/2 1
1
21/2
Рис. 2.10.5: Приклад 2.10.3 а)
Якщо цей результат {x =1} ,тостратегiяf
21
вказує гравцю P
1
,що
потрiбно вибирати
y =2,стратегiяf
12
вказує гравцю P
2
, що потрiбно
вибирати
z =2.ОскiлькиM(1,2,2) = 3,тогравецьP
2
платить гравцю
P
1
3 одиницi з ймовiрнiстю P {x =1} =1/2.
Якщо результат першого випадкового ходу
{x =2},тостратегiяf
21
вказує гравцю P
1
, що потрiбно вибирати y =1,стратегiяf
12
вказує
гравцю
P
2
, що потрiбно вибирати z =1.ОскiлькиM(2,1,1) = 5,то
гравець
P
2
платить гравцю P
1
5 одиниць з ймовiрнiстю P {x =2} =1/2.
Математичне сподiвання виграшу гравця
P
1
дорiвнює
3 ·
1
2
+5·
1
2
=
8
2
.
Природно розглядати це математичне сподiвання як виграш гравця P
1
в
тому випадку, коли вибранi стратегiя
f
21
гравця P
1
iстратегiяf
12
гравця
P
2
.
Аналогiчно обчислюємо виграшi гравця
P
1
, коли вибранi iншi пари стра-
тегiй гравцiв. Отримаємо матрицю 2.10.5. Ця матриця має сiдлову точку.
Цiна гри дорiвнює
3
2
. Оптимальною стратегiєю для гравця P
1
,якiдля
гравця
P
2
,єстратегiяf
11
.
Топологiчне дерево для випадку б) зображено на малюнку 2.10.6.
167

H
H
H
H
H
H
H
H
@
@
@
@
@
@
@
@
@
@
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
−2 2 −4 35 −3 −1 6
21212121
2222
2121
0
1
1/2 1
1
21/2
Рис. 2.10.6: Приклад 2.10.3 б)
2.10.1. Контрольнi запитання i задачi для самостiйної робо-
ти
1. Що таке позицiйна гра?
2. Як визначається нормальна форма позицiйної гри?
3. Що таке топологiчне дерево гри?
4. Що таке позицiйна гра з повною iнформацiєю?
5. Як визначається стратегiя поведiнки для гравця в позицiйнiй грi?
Задачi
1. У грi беруть участь два гравцi. Гравець P
1
робить перший хiд.
Вiн вибирає число
x iз множини {1,2}. Другий хiд випадковий.
Випадково вибирається число
y з множини {1,2}, P { y =1} =1/4,
P {y =2} =3/4.ГравецьP
2
робить третiй хiд. Вiн вибирає число z
iз множини {1,2},якщоy =1i вибирає z iз множини {1,2,3},якщо
168
y =2.ВкiнцiгригравецьP
2
платить гравцю P
1
суму M(x,y,z),де
функцiя
M(x,y,z) дорiвнює:
M(1,1,1) = 2, M(1,1,2) = −2, M (1,2,1) = 1, M(1,2,2) = 0, M (1,2,3) =
−4
, M(2,1,1) = 5, M(2,1,2) = −3, M(2,2,1) = 3, M (2,2,2) = −2,
M(2,2,3) = 0.
Iнформацiя, яку має гравець
P
2
:
а) гравець
P
2
знає x;
б) гравець
P
2
не знає x.
Зобразити гру у виглядi топологiчного дерева. Описати всi стратегiї
гравцiв. Знайти нормальну форму гри.
2. У грi беруть участь два гравцi. Гравець
P
1
робить перший хiд.
Вiн вибирає число
x з множини {1,2,3,4}.Другийхiд.ГравецьP
2
вибирає число y з множини {1,2}, знаючи чи парне x, чи нi. Третiй
хiд. Якщо
y =1, то випадково вибирається число z з множини
{1,2}, P {z =1} =1/10, P {z =2} =9/10.Якщоy =2,тогравець
P
1
вибирає число w iз множини {1,2},знаючиx, y.ГравецьP
2
платить гравцю P
1
суму M(x,y,z)=x + y − z, M(x,y,w)=xy − w.
Зобразити гру у виглядi топологiчного дерева. Описати всi стратегiї
гравцiв. Знайти нормальну форму гри.
3. Хiд перший. Гравець
P
1
вибирає число x з множини {1,2}.Другий
хiд випадковий. Випадково вибирається число
y з множини {1,2},
P {y =1} =1/5, P { y =2} =4/5. Третiй хiд. Якшо y =1,тогравець
P
2
,знаючиx та y, вибирає число z iз множини {1,2}.Якщоy =2,
то гравець
P
1
,знаючиx та y, вибирає число z iз множини {1,2}.
Функцiя виграшу задана у прикладi 2.
Зобразити гру у виглядi топологiчного дерева. Описати всi стратегiї
гравцiв. Знайти нормальну форму гри.
4. Гра двох гравцiв, у якiй гравець
P –одналюдина,агравецьQ
–командаiздвохлюдей:A, B. Всi три людини iзольованi одна
вiд одної. Спочатку суддя йде до гравця
P , який вибирає число x
з множини {1,2}.ЯкщоP вибирає число x =1,тосуддяйдедо
гравця
A, який вибирає число y з множини {1,2}.ЯкщоP вибирає
число
x =2,тосуддяйдедогравцяB iтойвибираєчислоy змно-
жини
{1,2}. Пiсля того, як вибрано число y,суддяйдедоiншого
члена команди
Q iтойвибираєчислоz з множини {1,2}.КомандаQ
платить командi P суму M(x,y,z),дефункцiяM(x,y,z) приймає та-
кi значення:
M(1,1,1) = 0, M (1,1,2) = 2, M(1,2,1) = 6, M (1,2,2) = 8,
169

M(2,1,1) = 4, M(2,1,2) = 0, M (2,2,1) = 5, M(2,2,2) = 6.Зобразити
гру у виглядi топологiчного дерева. Описати всi стратегiї гравцiв.
Знайти нормальну форму гри.
5. Хiд 1. Гравець
A вибирає число x ∈{1,2}.Хiд2.Випадкововиби-
рається
y ∈{1,2}, p
1
= p
2
=
1
2
.Хiд3.ГравецьB вибирає z ∈{1,2} .
В кiнцi гри гравець
A платить гравцю B одну одиницю, якщо
x + y + z =4,iнакшегравецьB одну одиницю платить A.Iнформа-
цiя, якою володiє гравець
B:
а) вiдомо значення
y, але не вiдомо значення x;
б) не вiдомо нi
x,нiy;
в) вiдомо i
x,iy;
г) вiдомо тiльки значення
x + y;
д) вiдомо тiльки значення
x − y.
Зобразити гру у виглядi топологiчного дерева. Описати всi стратегiї
гравцiв. Знайти нормальну форму гри.
6. Хiд 1. Гравець
A вибирає x ∈{1,2,3,4}.Хiд2.ГравецьB,знаючи
парне
x чи нi, вибирає y ∈ 1,2.Хiд3.Якщоy =1,товипадково
вибирається
z ∈{1,2}, p
1
=0,1, p
2
=0,9.Якщоy =2,тогравецьA,
знаючи
x та y, вибирає w ∈{1,2}.ВкiнцiгригравецьB платить A
суму, яка визначається значеннями функцiй M(x,y,z)=x+y−z або
M(x,y,w)=xy − w. Зобразити гру у виглядi топологiчного дерева.
Описати всi стратегiї гравцiв. Знайти нормальну форму гри.
7. Хiд 1. Гравець
A вибирає x ∈{1,2,...5}.Хiд2.ГравецьB вибирає
y ∈{1,2,...5},незнаючиx.ВкiнцiгригравецьB платить A суму
M(x,y),де
M(x,y)=
−2, |x − y| =1;
1, |x − y| > 1;
0,x= y.
Зобразити гру у виглядi топологiчного дерева. Описати всi стратегiї
гравцiв. Знайти нормальну форму гри.
8. Хiд 1. Гравець
A вибирає число x ∈{1,2}.Хiд2.Пiдкидається
монета. Якщо випав “герб” (i тiльки у цьому випадку), то гравцю
B
повiдомляється значення x.Хiд3.ГравецьB вибирає y ∈{3,4}.Хiд
4. Випадково вибирається
z ∈{1,2,3}, p
1
=0,4, p
2
=0,2, p
3
=0,4.
В кiнцi гри гравець
A платить гравцю B суму w = x + y + z,
якщо вона непарна, iнакше гравець
B цю суму A.Зобразитигруу
170
