Моклячук М.П., Ямненко Р.Є. Лекції з теорії вибору та прийняття рішень (на укр. языке)

Подождите немного. Документ загружается.

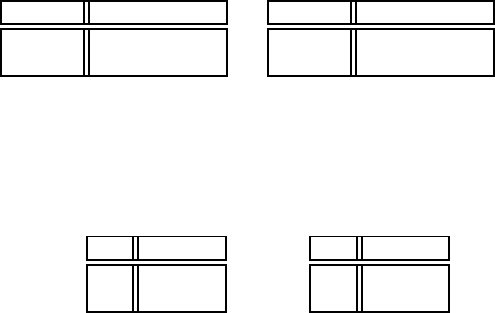
2) зважити купленi яблука на контрольних вагах i в разi виявлення

обману зажадати вiдшкодування збитку.

Назвемоцiстратегiї“повiрити”i“перевiрити”вiдповiдно,iвизначимо

виграшi продавця i покупця в кожнiй ситуацiї:

а) Продавець чесно зважив, а покупець йому повiрив. Вiдповiднi ви-

грашiобох,рiвнi0,виберемоякпочатоквiдлiку.

б) Продавець обдурив, а покупець йому повiрив. Виграш продавця

приймемо рiвним 1, оскiльки вiн одержав додатковий прибуток. Виграш

покупця рiвний

−1,оскiлькивiнодержавменшеяблук.

в) Продавець чесно зважив, а покупець його перевiрив. Виграш про-

давця рiвний 0. Нехай виграш покупця рiвний

−1/2:вiн,по-перше,да-

ремно згаяв час, а, по-друге, безглуздо себе вiдчуває.

г) Продавець обдурив, а покупець його перевiрив. Виграш продавця

приймемо рiвним

−1, оскiльки виявлення обману загрожує йому певни-

ми неприємностями (наприклад, його можуть позбавити лiцензiї на тор-

гiвлю на цьому ринку). Виграш покупця рiвний 1/2, оскiльки, по-перше,

йому вiдшкодували обважування, а, по-друге, вiн вiдчуває моральне за-

доволення вiд викриття обманщика.

Виходить наступна бiматрична гра:

Продавець

пов перев

чесн 00

обман 1 −1

Покупець

пов перев

чесн 0 −1/2

обман −11/2

Легко перевiрити, що в цiй грi немає рiвноваги Неша.

Такого типу iгри поширенi в моделях, що описують економiчнi i еко-

логiчнi взаємодiї. Розглянемо приклад гри, що має двi ситуацiї рiвнова-

ги.

Приклад 2.9.2. Гра “сiмейна суперечка”:

A =

ФТ

Ф 10

Т 02

B =

ФТ

Ф 20

Т 01

Iнтерпретацiя. Дружина (перший гравець) i чоловiк (другий гравець)

обговорюють питання, куди пiти розважитися: на футбол (стратегiя 1)

або в театр (стратегiя 2). Якщо йдуть на футбол, то дружина одержує

1 одиницю, а чоловiк одержує 2 одиницi “задоволення”. Якщо йдуть в

театр, то виграш дружини дорiвнює 2, а виграш чоловiка дорiвнює 1.

Якщо ж обоє йдуть в рiзнi мiсця, то виграшi гравцiв нульовi.

У грi iснує двi ситуацiї рiвноваги:

(1,1) та (2,2). Перша з них вигiднi-

ша другому гравцю, а друга – першому. Якщо гравцi дiятимуть незале-

141

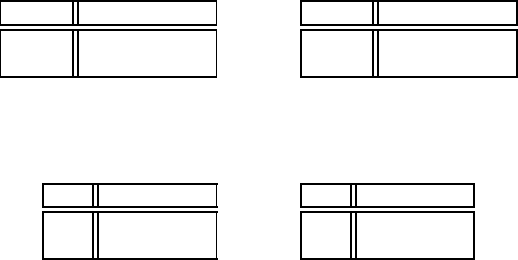
жно, то перший, напевно, вибере стратегiю 2, а другий – стратегiю 1. В

результатi обидва одержать по нулю.

Даний приклад показує, що необхiдний якийсь механiзм координацiї

при виборi стратегiї, якщо iснує декiлька рiвноваг Неша. Тому такi iгри

називають також “iграми на координацiю”.

Використання ситуацiй рiвноваги на практицi часто пов’язується з

таким сценарiєм поведiнки гравцiв. Вони спочатку повиннi домовитися

про ситуацiю рiвноваги, потiм всякi переговори забороняються i гравцi

незалежно вибирають свої стратегiї, можливо порушуючи прийняту уго-

ду. Вiдмiтимо, що одному гравцю буде невигiдно вiдхилятися вiд своєї

рiвноважної стратегiї. Якщо гравцi дотримуються в грi такого сценарiю

поведiнки, то гра

Γ називається безкоалiцiйною.

Приведемо ще один приклад “гри на координацiю”.

Приклад 2.9.3. Гравцями є два водiї, яким потрiбна проїхати через пе-

рехрестя, до якого вони пiд’їхали одночасно. Є двi стратегiї перетину

перехрестя: використовувати “правило правої руки”, згiдно якому водiй

повинен пропустити перешкоду справа (стратегiя 1), або “правило лi-

вої руки”, згiдно якому водiй повинен пропустити перешкоду лiворуч

(стратегiя 2). Якщо обидва водiї дотримуються одного правила, то вони

успiшно роз’їдуться, але якщо один з них використовує “правило правої

руки”, а iнший “правило лiвої руки”, то може виникнути аварiя. Отже,

для сприятливого результату в таких iграх у всiх гравцiв повинен бути

однаковий пiдхiд до вибору правил поведiнки.

Маємотакубiматричнугру:

A =

пр.п лiв.п

пр.п 1 −10

лiв.п −1 0

B =

пр.п лiв.п

пр.п 0 −10

лiв.п −1 1

Наведемо приклад, який показує, що рiвновага Неша може бути не-

ефективною для iнтересiв гравцiв.

Приклад 2.9.4. Гра “дилема ув’язненого”:

A =

пр нi

пр −8 0

нi −10 −1

B =

пр нi

пр −8 −10

нi 0 − 1

Iнтерпретацiя. Два бандити (гравцi 1 i 2), якi пiдозрюються в скоєннi

тяжкого злочину, перебувають iзольовано один вiд одного в попередньо-

му ув’язненнi. Зважаючи на вiдсутнiсть прямих доказiв успiх або неуспiх

звинувачення залежить вiд зiзнання (стратегiя 1) або не зiзнання (стра-

тегiя 2) самих бандитiв. Якщо обидва бандити признаються (ситуацiя

142

(1,1)), то вони будуть визнанi винними i засудженi до 8 рокiв ув’язнен-

ня. Якщо жоден з них не признається (ситуацiя

(2,2)), то вони будуть

виправданi, але обвинувачу все-таки вдасться довести їх провиннiсть в

деякому супутньому менш тяжкому злочинi, наприклад, в носiннi зброї,

внаслiдок чого вони будуть засудженi до 1 року ув’язнення. Якщо, на-

рештi, признається лише один з них (ситуацiї

(2,1) i (1,2)), то вiн буде

звiльнений (за допомогу слiдству), а iнший буде засуджений на макси-

мальний термiн – 10 рокiв.

У цiй грi наявна єдина ситуацiя рiвноваги

(1,1):обомпризнатися.

Проте є ситуацiя

(2,2), вигiднiша обом гравцям, яка не є ситуацiєю

рiвноваги. Отже, рiвноваги Неша можуть бути неефективнi в тому сенсi,

що за рахунок вiдхилення обох гравцiв вiд ситуацiї рiвноваги можна

полiпшити виграшi кожного з них.

У зв’язку з останнiм прикладом дамо визначення ситуацiї, оптималь-

ної за Парето.

Означення 2.9.4. Ситуацiя

) гри Γ називається оптимальною за

Парето,якщонеiснуєтакоїситуацiї

(x,y),щовиконанiнерiвностi

F (x,y) ≥ F (x

),G(x,y) ≥ G(x

)

i принаймнi одна нерiвнiсть строга.

В останньому прикладi в ситуацiї

(2,2) обидва гравцi отримують по

−1, що бiльше, нiж їх виграш −8 уситуацiїрiвноваги(1,1).Отже,си-

туацiя рiвноваги не є оптимальною за Парето.

Наступний приклад показує, що не завжди рiвноважнi стратегiї яв-

ляються максимiнними.

Приклад 2.9.5. Нехай

A =



205

223



,B=



221

078



Тут (1,1) – єдина ситуацiя рiвноваги, проте стратегiя 1 першого грав-

ця не є максимiнною. Дiйсно,

W (1) = min

1≤j≤3

=0,W(2) = min

1≤j≤3

=2.

Стратегiя 1 другого гравця також не є максимiнною. Якщо гравець недо-

брозичливо настроєний по вiдношенню до партнера, то вiн може поруши-

ти угоду i замiсть рiвноважної стратегiї вибрати максимiнну. В резуль-

татi вiн отримає той же виграш 2, що i в ситуацiї рiвноваги, а партнер

отримає 0.

Ми вiдзначили три недолiки поняття рiвноваги Неша:

1)рiвновагиНешавгрiможенеiснувати;

143

2)рiвновагаНешаможебутинеєдиною;

3) рiвновага Неша може бути неефективною.

Незважаючи на цi недолiки, вказане поняття грає центральну роль в

теорiї прийняття рiшень в конфлiктних ситуацiях.

Приведемо теорему iснування ситуацiї рiвноваги в грi двох осiб. Пе-

ред цим сформулюємо топологiчну теорему про нерухому точку.

Теорема 2.9.1. (Теорема Брауера про нерухому точку). Нехай

f : Z →

– неперервне вiдображення в себе опуклого компакта (замкнутої

обмеженої множини)

Z скiнченовимiрного евклiдового простору R

Тодi у нього iснує нерухома точка

: f(z

)=z

Вiдзначимо, що всi умови теореми iстотнi. Наприклад, якщо множина

Z не опукла, то твердження теореми може бути невiрним. Дiйсно, якщо

Z –коло,аf – її поворот на кут α<2π,тоf нерухомої точки не має.

Теорема 2.9.2. Нехай в грi двох осiб

Γ множини X i Y –опуклi

компакти евклiдових просторiв

i R

. Припустимо, що функцiї

F (x,y) i G(x,y) неперервнi на X × Y ,функцiяF (x,y) угнута по x при

будь-якому фiксованому

y,афункцiяG(x,y) угнута ???? при будь-

якому фiксованому

x.ТодiвгрiΓ iснує ситуацiя рiвноваги.

Доведення. Спочатку припустимо, що функцiї

F (x,y) i G(x,y) неперервнi

на

X × Y i строго угнутi за змiнними x та y вiдповiдно. Тодi для будь-

яких стратегiй

y та x множини найкращих вiдповiдей гравцiв

X(y) = arg max

x∈X

F (x,y)={x(y)},Y(x) = arg max

y∈Y

G(x,y)={y(x)}

мiстять по одному елементу x(y) та y(x).Функцiїx(y) та y(x) неперерв-

нi. Називатимемо їх функцiями найкращої вiдповiдi першого i другого

гравцiв вiдповiдно.

Покладемо

Z = X ×Y i розглянемо вiдображення f : Z → Z, f (x,y)=

(x(y),y(x))

. За попередньою теоремою вiдображення f має нерухому то-

чку

=(x

):f(z

)=z

,абоx(y

)=x

,y(x

)=y

.Отже,(x

) –

ситуацiя рiвноваги.

Тепер припустимо, що функцiї

F (x,y) i G(x,y) угнутi за змiнними x

та y, але не обов’язково строго. Покладемо

(x,y)=F (x,y) − ε



i=1

(x,y)=G(x,y) −ε



i=1

де ε>0.ФункцiїF

(x,y) i G

(x,y) неперервнi на X ×Y .функцiяF

(x,y)

строго угнута по x,афункцiяG

(x,y) строго угнута по y.Угрi

= X,Y,F

(x,y),G

(x,y)

iснує ситуацiя рiвноваги (x

).Нехай{ε

} – така послiдовнiсть чисел,

що

{ε

}→0+ i вiдповiдна послiдовнiсть ситуацiй рiвноваги {(x

)}

144

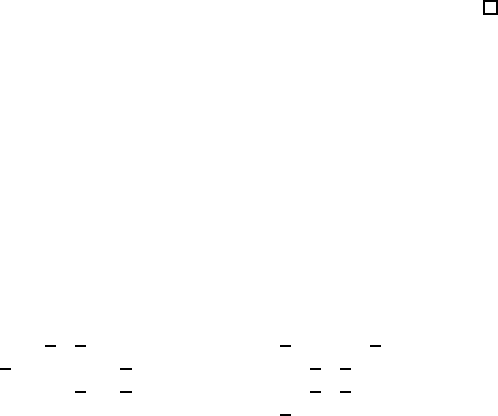
сходиться до деякої ситуацiї (x

). За визначенням {(x

)}

∀x ∈ XF

(x,y

) ≤ F

∀y ∈ YG

,y) ≤ G

Переходячи при фiксованих x та y до границi при {ε

}→0+,одержимо

∀x ∈ XF(x,y

) ≤ F (x

); ∀y ∈ YG(x

,y) ≤ G(x

Це означає, що (x

) – ситуацiя рiвноваги гри Γ.

Розглянемо метод пошуку ситуацiї рiвноваги з використанням мно-

жин найкращих вiдповiдей

X(y) = arg max

x∈X

F (x,y)={x(y)},Y(x) = arg max

y∈Y

G(x,y)={y(x)}.

Вiн полягає в розв’язуваннi системи включень

∈ X(y

),y

∈ Y (x

). (2.9.2)

У тому випадку, коли у гравцiв iснують неперервнi функцiї найкращої

вiдповiдi

x(y) i y(x) (див. першу частину доведення теореми), система

включень (2.9.2) еквiвалентна системi рiвнянь

x(y

)=x

,y(x

)=y

Приклад 2.9.6. Знайдемо всi ситуацiї рiвноваги гри Γ:

A =



5 −1

−23 4

2154

−1253



,B=



547

455 4

−36

6 2

736



УматрицiA пiдкресленi найбiльшi елементи в стовпцях, а в матри-

цi

B пiдкресленi найбiльшi елементи в рядках. Спiльний пiдкреслений

елемент вiдповiдає

(3,3) – єдинiй ситуацiї рiвноваги.

Приклад 2.9.7. Розглянемогрудвохосiб

Γ=X,Y,F(x,y),G(x,y),де

X, Y та F (x,y),G(x,y) – множина стратегiй i функцiї виграшу першого i

другого гравцiв. Нехай

X = Y =[0,1],F(x,y)=−3x

+2y

+7xy, G(x,y)=− (x + y − 1)

Функцiї F (x,y) i G(x,y) строго угнутi за змiнними x та y вiдповiдно.

Функцiї найкращої вiдповiдi

x(y)=



7y/6, 0 ≤ y ≤ 6/7,

1, 6/7 <y≤ 1,

y(x)=1− x.

Розв’язуючи систему x(y)=x,y(x)=y,знаходимоx

=7/13,y

=6/13.

Наступний приклад показує, що для пошуку рiвноваги Неша можна

використовувати необхiднi умови оптимальностi першого порядку.

145

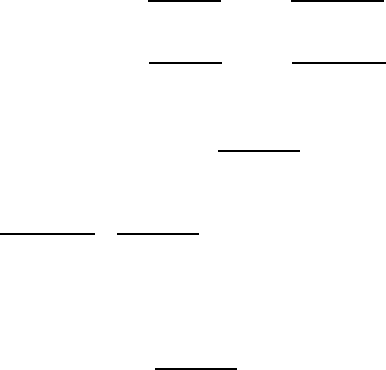
Приклад 2.9.8. Модель дуополiї. Двi фiрми випускають товар для про-

дажу на ринку. Нехай

x та y – кiлькостi товару, що випускається пер-

шою i другою фiрмами, а

0 <c

≤ c

– витрати на його виробни-

цтво, тобто собiвартостi одиницi товару для обох фiрм. Цiна товару

p(x + y) залежить вiд загального випуску x + y. Функцiї виграшу фiрм

F (x,y)=(p(x+ y)−c

)x та G(x,y)=(p(x+y)−c

)y – прибутки, отриманi

вiд реалiзацiї виробленої продукцiї.

Нехайцiнанапродукцiювизначаєтьсязаформулою

p(x+y)=K/(x+

,де1 ≥ α>0.Тодiможнавважати,щоX =[0,(K/c

)

1/α

],оскiльки

при

x>(K/c

)

1/α

перша фiрма терпить збитки при будь-якiй стратегiї

другої фiрми. Аналогiчно

Y =[0,(K/c

)

1/α

Вiдмiтимо, що для даної гри виконанi умови теореми 2.9.2 i ситуацiя

рiвноваги

) iснує. Нехай x

> 0,y

> 0. Тодi рiвноважнi стратегiї

знаходяться з системи рiвнянь



)

− c

−

αKx

)

α+1

=0,



)

− c

−

αKy

)

α+1

=0,

Додаючи рiвняння, знаходимо спочатку суму

+ y



(2 − α)K

+ c



1/α

апотiм

α(2 − α)K



(2 − α)K

+ c



(α+1)/α

+(α − 1)c

Оскiльки y

> 0,тонеобхiднощобc

+(α − 1)c

> 0.Якщовиконано

нерiвнiсть

+(α − 1)c

≤ 0, то перша фiрма є монополiстом на ринку i

рiвноважнi стратегiї мають вигляд:



(1 − α)K



1/α

=0.

Розглянемо змiшанi розширення бiматричних iгор Γ,щозадаються

матрицями

A =(a

)

m×n

,B=(b

)

m×n

Змiшанi стратегiї гравцiв у бiматричнiй грi Γ, як i в матричнiй грi, це

розподiли ймовiрностей на множинах чистих стратегiй гравцiв. Множи-

ну всiх змiшаних стратегiй першого гравця позначимо через



X =(x

,...,x

):x

≥ 0,





146

Вiдповiдно множину всiх змiшаних стратегiй другого гравця позначимо

через



Y =(y

,...,y

):y

≥ 0,





Якщо перший гравець застосував змiшану стратегiю X =(x

,...,x

), а

другий гравець застосував змiшану стратегiю

Y =(y

,...,y

),товиграш

першого гравця визначається математичним сподiванням

A(X,Y )=



i=1



j=1

а виграш другого гравця – математичним сподiванням

B(X,Y )=



i=1



j=1

В результатi одержали змiшане розширення бiматричної гри

Γ=S

,A(X,Y ),B(X,Y ).

Ситуацiї рiвноваги гри Γ називатимемо ситуацiями рiвноваги в змiшаних

стратегiях (або змiшаними рiвновагами Неша) початкової гри

Γ.

Множина змiшаних стратегiй

та S

– опуклi компакти евклiдових

просторiв

та R

,афункцiїA(X,Y ) та A(X,Y ) бiлiнiйнi. За теоремою

(2.9.2) в грi

Γ iснує ситуацiя рiвноваги в змiшаних стратегiях (X

Для неї за визначенням виконанi нерiвностi

A(X,Y

) ≤ A(X

) ∀X ∈ S

B(X

,Y ) ≤ A(X

) ∀Y ∈ S

Розглянемо властивостi ситуацiй рiвноваги в змiшаних стратегiях, ана-

логiчнi властивостям ситуацiй рiвноваги матричних iгор.

Лема 2.9.1. Для того, щоб ситуацiя

) була ситуацiєю рiвнова-

ги в змiшаних стратегiях бiматричної гри

Γ,необхiдноiдостатньо,

щоб виконувались умови

A(i,Y

) ≤ A(X

),i=1,...,m; (2.9.3)

B(X

,j) ≤ A(X

),j=1,...,n. (2.9.4)

Доведення. Необхiднiсть. Нехай

) –ситуацiярiвноваги.Тодi

A(X,Y

) ≤ A(X

) ∀X ∈ S

Звiдки для X = e

(i-та чиста стратегiя) одержимо нерiвностi (2.9.3) для

матрицi

A. Аналогично виводяться нерiвностi (2.9.4) для матрицi B.

Достатнiсть. Нехай ситуацiя

) задовольняє нерiвностi (2.9.3),

(2.9.4). Вiзьмемо будь-яку змiшану стратегiю

X =(x

,...,x

) першого

147

гравця, домножимо нерiвностi A(i,Y

) ≤ A(X

) на x

iдодамоїх.В

результатi одержимо нерiвнiсть

A(X,Y

) ≤ A(X

).Аналогiчно,для

будь-якої стратегiї

Y =(y

,...,y

) другого гравця доводиться нерiвнiсть

B(X

,Y ) ≤ A(X

Теорема 2.9.3. (Властивiсть доповнюючої нежорсткостi). Нехай (X

) – ситуацiя рiвноваги в змiшаних стратегiях бiматричної гри Γ.

Тодi

1) x

> 0 ⇒ A(i,Y

)=A(X

);

2) y

> 0 ⇒ B(X

,j)=B(X

Доведення. Доведемо твердження 1). Припустимо, що для деякого i

виконується нерiвнiсть x

> 0 i A(i,Y

) <A(X

). Кожну нерiвнiсть

A(i,Y

) ≤ A(X

) з (2.9.3) помножимо на x

i додамо їх. Оскiльки

-а нерiвнiсть строга, то одержимо A(X

) <A(X

) (протирiччя).

Твердження 2) доводиться аналогiчно.

Наслiдок. Нехай (X

) – ситуацiя рiвноваги в змiшаних стратегi-

ях бiматричної гри

Γ.Тодi

1) A(i,Y

) <A(X

) ⇒ x

=0;

2) B(X

,j)=B(X

) ⇒ y

=0.

Теорема 2.9.4. Для того, щоб ситуацiя (X

) була ситуацiєю рiв-

новаги в змiшаних стратегiях бiматричної гри

Γ,необхiдноiдоста-

тньо, щоб знайшлася множини

⊂ P , Q

⊂ Q iчислаv

, v

,для

яких виконуються умови













j∈Q

= v

,i∈ P



j∈Q

≤ v

,i/∈ P



j∈Q

=1,y

≥ 0,j∈ Q

(2.9.5)









i∈P

= v

,j∈ Q



i∈P

≤ v

,j/∈ Q



i∈P

=1,x

≥ 0,i∈ P

(2.9.6)

Доведення. Необхiднiсть. Нехай

) –ситуацiярiвноваги.Покла-

демо

= A(X

), v

= B(X

= {i ∈ P : x

> 0},Q

= {j ∈ Q: y

> 0}.

Умови (2.9.5) i (2.9.6) є наслiдком леми 2.9.1 та теореми 2.9.3.

Достатнiсть. Нехай для ситуацiї

) виконанi умови (2.9.5) i

(2.9.6). Покажемо, що тодi

A(X

)=v

. Дiйсно, з (2.9.5) випливає,

що

148



j∈Q



j=1

= v

,i∈ P

Помноживши цi рiвностi на x

,i ∈ P

,iдодавшиїх,одержимоA(X

.Аналогiчнодоводиться,щоB(X

)=v

. За лемою 2.9.1 (X

) є

ситуацiєю рiвноваги.

Опишемо алгоритм пошуку ситуацiй рiвноваги в змiшаних стратегiях.

Перебираємо квадратнi пiдматрицi

A =(a

)

i∈P

,j∈Q

, B =(b

)

i∈P

,j∈Q

та розв’язуємо системи рiвнянь з (2.9.5) i (2.9.6). Якщо розв’язки цих

систем

,i ∈ P

i y

,i ∈ Q

задовольняють нерiвностi з умов (2.9.5)

i (2.9.6), то, додаючи компоненти

=0,i /∈ P

i y

=0,i /∈ Q

,одер-

жимо ситуацiю рiвноваги

). За скiнченне число крокiв алгоритм

приводить до ситуацiї рiвноваги.

Проiлюструємо роботу алгоритму для iгор з матрицями розмiрiв

2×n:

A =



··· a



,B=



··· b



В даному випадку змiшана стратегiя першого гравця має вигляд (x,1−x),

де

0 ≤ x ≤ 1. Перебирати потрiбно 2 ×2-матрицi. Кожна з них задається

номерами двох стовпцiв

. Запишемо систему (2.9.6)

+(1−x

= v

+(1−x

= v

+(1− x

≤ v

,j= j

,0 ≤ x

≤ 1.

Якщо ця система несумiсна, то перейдемо до iншої пари j

.Якщо

розв’язок

системи (2.9.6) iснує, то розглянемо систему (2.9.5)

+(1−y

= v

+(1−y

= v

, 0 ≤ y

≤ 1.

Нехай iснує її розв’язок y

. Визначимо компоненти стратегiї другого

гравця







,j= j

1 − y

,j= j

0,j= j

Тодi ситуацiя (X

) буде змiшаною рiвновагою Неша.

Такому алгоритму можна дати геометричну iнтерпретацiю. На вiдрiз-

ку

0 ≤ x ≤ 1 будуємо прямi l

(x)=b

x + b

(1 − x),j =1,...,n.Точки

зламу злому верхньої огинаючої сiмейства прямих

(x),j =1,...,n вiд-

повiдають парам

, для яких iснує розв’язок x

системи (2.9.6).

Послiдовно перебираємо точки верхньої огинаючої сiмейства прямих i

розв’язуємо систему рiвнянь з (2.9.5) перевiряючи нерiвностi

0 ≤ y

≤ 1.

149

При n =2обидвi матрицi A та B мають розмiрнiсть 2 × 2.Вцьому

випадку прямi

(x)=b

x + b

(1 −x), l

(x)=b

x + b

(1 −x) перетина-

ються в точцi

0 ≤ x

≤ 1 тодi i тiльки тодi, коли виконується нерiвнiсть

− b

)(b

− b

) ≥ 0. (2.9.7)

Якщо стовпцi матрицi

B (i вiдповiднi прямi l

i l

)неспiвпадають,то

компоненти змiшаної стратегiї

, що задовольняють систему (2.9.6),

можна записати в явному виглядi

− b

+ b

− b

+ b

− b

. (2.9.8)

Для системи (2.9.5), з якої обчислюється змiшана стратегiя другого

гравця, всi мiркування проводяться аналогiчним чином. В результатi ми

одержимо наступну умову на матрицю першого гравця, що забезпечує

iснування розв’язку системи (2.9.5):

− a

)(a

− a

) ≥ 0. (2.9.9)

Цю умову можна виписати, виходячи з таких мiркувань: потрiбно замi-

нити другого гравця першим i врахувати, що другий гравець вибирав

свої стратегiї за стовпцями, а перший вибирає їх за рядками. Тому щоб

виписати умови iснування розв’язку, потрiбно виписати умову (2.9.7), за-

мiнивши одну матрицю на iншу, а рядки на стовпцi. Якщо рядки матрицi

A не спiвпадають, то компоненти змiшаної стратегiї Y

що задовольня-

ють систему (2.9.5), можна записати в явному виглядi

− a

+ a

− a

+ a

− a

. (2.9.10)

Приклад 2.9.9. Модель технiчного контролю за якiстю продукцiї. Завод

випускає автомобiлi партiями по 100 штук. За кожну автомашину завод

одержує вiд концерну 1.3 од. оплати, з яких 1 од. складають премiаль-

нi, а 0.3 од. призначенi для операцiй технiчного контролю (ОТК). Завод

(гравець 1) може випускати партiю автомобiлiв або з ОТК (стратегiя 1),

або без ОТК (стратегiя 2), збiльшуючи суму премiальних. При викори-

станнi першої стратегiї пiдсумкова сума премiальних, одержаних заводом

за партiю, складає 100 од., а при використаннi другої стратегiї – 130 од.

З метою зменшення виробничого браку концерн вирiшив використати

незалежну фiрму, яка здiйснює технiчний контроль за якiстю продукцiї.

Вартiсть перевiрки автомобiля для фiрми складає 0.12 од. Якщо ОТК

заводом не проводиться, то автомобiль несправний з ймовiрнiстю 4/5.

В разi виявлення несправностей завод зобов’язаний їх усунути, витра-

тивши 0.3 од., i заплатити додатково фiрмi 0.2 од. зi своїх премiальних.

Фiрма (гравець 2) може або перевiрити партiю (стратегiя 1), або вiдмо-

витися вiд її перевiрки (стратегiя 2).

Виграшем першого гравця є очiкувана сума премiальних, одержана

заводом вiд концерну за партiю автомобiлiв з врахуванням витрат на

150