Моклячук М.П., Ямненко Р.Є. Лекції з теорії вибору та прийняття рішень (на укр. языке)

Подождите немного. Документ загружается.

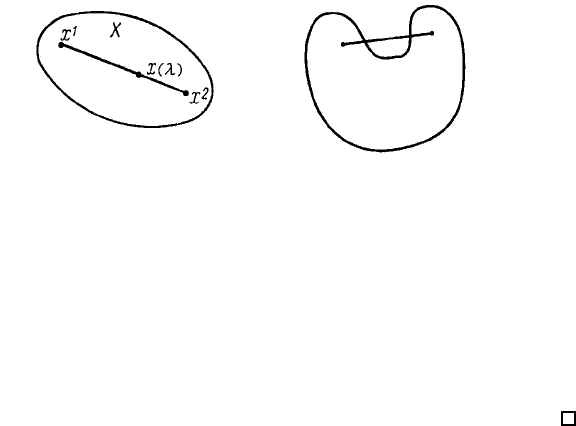
1) пряма, що проходить через точку ˆx унапрямкуh

ˆxh

= {x ∈ R

: x =ˆx + αh ,α ∈ R} ;

2) промiнь, що виходить з точки ˆx унапрямкуh

ˆxh

= {x ∈ R

: x =ˆx + αh ,α ∈ R ,α ≥ 0};

3) гiперплощина з нормаллю p ∈ R

pβ

= {x ∈ R

: p,x = β};

4) пiвпростори, що породженi цiєю гiперплощиною

pβ

= {x ∈ R

: p,x≥β};

−

pβ

= {x ∈ R

: p,x≤β}.

Рис. 1.3.1: Опукла множина. Неопукла множина.

Теорема 1.3.1. Нехай I – множина iндексiв (скiнченна чи нескiнченна),

та нехай

,i ∈ I, – опуклi множини. Перетин X =



i∈I

опуклих

множин є опуклою множиною.

Доведення. Нехай

∈ X,λ ∈ [0,1]. За означенням перетину x

∈

для всiх i ∈ I.ОскiлькиX

– опуклi множини, то x = λx

+(1−λ)x

∈

для всiх i ∈ I.Томуx ∈



i∈I

= X.Отже,множинаX =



i∈I

опукла.

Так само просто доводиться i наступна теорема.

Теорема 1.3.2. Нехай

,...,X

– опуклi множини, a

,...,a

–до-

вiльнi числа. Тодi опуклою є множина



i=1





x =



i=1

∈ X

,i=1,...,m



що називається лiнiйною комбiнацiєю множин X

,...,X

Як наслiдок, опуклими є сума i рiзниця опуклих множин

± X



x|x = x

± x

∈ X



Означення 1.3.3. Опуклою комбiнацiєю точок x

,...,x

n-вимiрного

простору

називається точка

x =



i=1

,λ

≥ 0,



i=1

=1, (1.3.1)

де

=(x

,...,x

) ∈ R

,i=1,...,m.

Теорема 1.3.3. Опукла множина мiстить всi можливi опуклi комбi-

нацiї своїх точок.

Доведення. Треба показати, що для довiльного

m =1,2,... зумов

x =



i=1

∈ X, λ

≥ 0,i=1,...,m;



i=1

=1, (1.3.2)

випливає

x ∈ X. Проведемо iндукцiю за m.Якщоm =1,товипадок

тривiальний. Якщо

m =2, то твердження теореми випливає з означення

опуклої множини. Припустимо, що твердження доведене для

m = k,i

нехай (1.3.2) виконується при

m = k +1.Якщоλ

k+1

=1,тоλ

= ... =

=0,i,вiдповiдно,x = x

k+1

∈ X.Якщожλ

k+1

< 1,томиможемо

записати

x =(1− λ

k+1

)x + λ

k+1

, x =



i=1

1 − λ

k+1

. (1.3.3)

Точка

x – це опукла комбiнацiя точок x

,...,x

. Тодi за припущенням

iндукцiї

x ∈ X. З (1.3.3) з урахуванням опуклостi X випливає, що

x ∈ X.

Означення 1.3.4. Перетин всiх опуклих множин з R

,щомiстятьдану

множину

X, називається опуклою оболонкою множини X iпозначається

conv

Для будь-якої множини

X ⊂ R

її опукла оболонка conv X непоро-

жня (оскiльки

X мiститься щонайменше в просторi R

,якийєопуклою

множиною). Якщо множина

Y опукла i мiстить X, то за означенням

conv

X ⊂ Y . Iншими словами, convX – найменша опукла множина, яка

мiстить

X. Зрозумiло, що множина X опукла тiльки в тому випадку

коли conv

X = X.

Теорема 1.3.4. Опукла оболонка довiльної множини

X спiвпадає з

множиною всiх опуклих комбiнацiй точок з

Доведення. Позначимо через

Z множину всiх можливих опуклих комбi-

нацiй точок з

X. Потрiбно показати, що conv X = Z.Перевiримо,щоZ

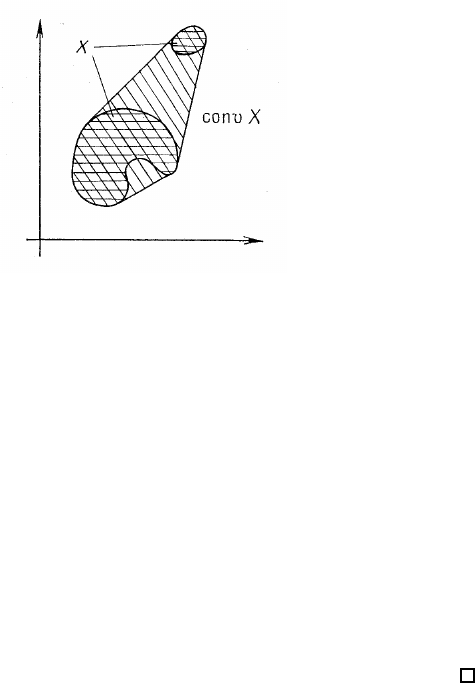
Рис. 1.3.2: Опукла оболонка.

опукла. Нехай x,y ∈ Z, λ ∈ [0,1]. За означенням Z маємо:

x =



i=1

∈ X, µ

≥ 0,i=1,...,m;



i=1

=1,

y =



k=1

∈ X, η

≥ 0,k=1,...,s;



k=1

=1.

При цьому точка z = λx +(1− λ) y є лiнiйною комбiнацiєю точок x

,...,

, ..., y

з невiд’ємними коефiцiєнтами λµ

,...,λµ

, (1 − λ) η

, ...,

(1 − λ) η

, якi в сумi дорiвнюють одиницi. Iншими словами, z –опукла

комбiнацiя вказаних точок з

X i X ⊂ Z.Втойжечасбудь-якаопукла

множина

Y , що мiстить X, мiстить i Z в силу теореми 1.3.3. Тому i

перетин всiх таких

Y ,тобтоconvX, мiстить Z. Тому conv X ⊃ Z.Отже,

conv

X = Z.

Теорема 1.3.4 стверджує, що будь-яку точку з conv X можна предста-

вити у виглядi опуклої комбiнацiї точок з

X,кiлькiстьяких,звичайно,

не дуже велика. Виявляється, що для

X ⊂ R

це число завжди можна

обмежити величиною

n +1. Це твердження, вiдоме як теорема Каратео-

дорi, є одним з найважливiших фактiв у скiнченновимiрному опуклому

аналiзi.

Теорема 1.3.5. (Теорема Каратеодорi) У просторi

будь-яку точку

зconv

X можна подати у виглядi опуклої комбiнацiї не бiльш нiж n+1

точок iз X, тобто для будь-якого x iз conv X знайдуться x

,...,x

∈

такi, що x = λ

+ ···+ λ

,λ

> 0,i =1,...,r; λ

+ ···+ λ

=1, де

r ≤ n +1.

Доведення. Зрозумiло, що центральним мiсцем у теоремi є тверджен-

ня про те, що

r ≤ n +1. Вiзьмемо точку вигляду (1.3.2) i покажемо,

що число ненульових доданкiв у сумi (1.3.2) можна зменшити, якщо

m>n+1.Припустимо,щовсiλ

> 0. Вiзьмемо (n +1)-вимiрнi вектори

,1),i =1,...,m,уякихпершin компонент збiгаються з вiдповiдними

компонентами вектора

, а остання компонента дорiвнює 1. Оскiльки

число таких векторiв

m>n+1, то вони лiнiйно залежнi. Тому знайду-

ться не всi рiвнi нулю числа

,i =1,...,m,такi,що



i=1

=0,



i=1

=0.

Серед чисел α

обов’язково є додатнi в силу останнього спiввiдношення.

Покладемо

=min



: α

> 0 ,i =1,...,m



Нехай мiнiмум досягається при деякому i = i

.Тодi

= λ

− ε

≥ 0,i=1,...,m.

Це очевидно для α

≤ 0,адляα

> 0 випливає з вибору ε

.Теперiз

спiввiдношень



i=1



i=1

− ε



i=1

= x,



i=1



i=1

− ε



i=1

випливає, що точку x можна подати у виглядi опуклої комбiнацiї меншої

кiлькостi ненульових доданкiв. Так зменшувати можна доти, доки

n +1

. Звiдси i випливає твердження теореми.

Означення 1.3.5. Многогранною множиною називається перетин скiн-

ченної кiлькостi пiвпросторiв. Обмежена многогранна множина називає-

ться многогранником.

Як наслiдок теореми 1.3.1 маємо таку теорему.

Теорема 1.3.6. Многогранна множина опукла.

1.3.2. Проекцiя точки на множину

Означення 1.3.6. Проекцiєю точки a ∈ R

на множину X ⊂ R

назива-

ється точка

(a) ∈ X така, що π

(a) − a≤x − a для всiх x ∈ X,

тобто найближча точка до

a серед усiх точок x iз X.

Якщо a ∈ X,тоπ

(a)=a.Якщоa ∈ X i множина X вiдкрита, то

проекцiї

(a) не iснує.

Рис. 1.3.3: Проекцiя точки на множину.

Теорема 1.3.7. Нехай X –замкнутаопукламножинавR

iточка

a ∈ X. Тодi iснує єдина проекцiя π

(a) точки a на X iвонамаєтакi

властивостi:

π

(a) − a,x − π

(a)≥0 для всiх x ∈ X, (1.3.4)

π

(a) − a,x − a≥π

(a) − a

> 0 для всiх x ∈ X. (1.3.5)

Геометрично це означає, що вектори

(a) − a та x − π

(a) утворю-

ють нетупий кут, а кут мiж

(a) − a та x − a гострий.

Доведення. Вiзьмемо довiльну точку

ˆx ∈ X,числоR = ˆx−a iутворимо

множину

X = {x ∈ X : x − a≤R}.

Вона непорожня, замкнута i обмежена. Неперервна функцiя f (x)=x −

a

досягає мiнiмального значення на

уточцix

∗

.Цяточкабудеточкою

мiнiмуму функцiї

f(x)=x − a i на множинi X. Отже, проекцiя x

∗

(a) точки a на множину X iснує.

Щоб довести єдинiсть проекцiї

∗

= π

(a) точки a на множину X,

припустимо, що iснують рiзнi точки

∈ X, x

= x

,щоє

проекцiями точки

a на множину X,тобтоx

− a = x

− a = δ.

Оскiльки множина

X опукла, то точка z =

+ x

) ∈ X. Проте з

теореми Пiфагора випливає, що

a − z

x

− a

x

− a

= δ

А це суперечить визначенню проекцiї точки на множину X.

Щоб довести спiввiдношення (1.3.4), помiтимо, що для всiх

x ∈ X i

λ ∈ [0,1] зопуклостiX випливає спiввiдношення

x

∗

− a

≤

λx +(1−λ)x

∗

− a

= (x

∗

− a)+λ(x − x

∗

)

= x

∗

− a

+2λx

∗

− a,x − x

∗

 + λ

x − x

∗



Тому

2x

∗

− a,x − x

∗

 + λx − x

∗



≥ 0.

Перейдемо до границi при λ → 0 i отримаємо спiввiдношення (1.3.4).

Спiввiдношення (1.3.5) отримаємо якщо додамо

±a до другого спiв-

множника скалярного добутку з спiввiдношеннi (1.3.4) i врахуємо, що

(a) = a оскiльки a ∈ X, π

(a) ∈ X.

1.3.3. Роздiляючi та опорнi гiперплощини

Означення 1.3.7. Множини X

та X

зпросторуR

1) роздiляються,якщоiснуютьp ∈ R

,p =0, та β ∈ R такi, що

p,x

≥β ≥p,x

∀x

∈ X

, ∀x

∈ X

; (1.3.6)

2) власне роздiляються, якщо iснують такi

p та β,щовиконується

(1.3.6) i, крiм того,

p,ˆx

 > p,ˆx

при деяких ˆx

∈ X

, ˆx

∈ X

; (1.3.7)

3) сильно роздiляються, якщо iснують такi

p та β,що

inf

∈X

p,x

 >β> sup

∈X

p,x

. (1.3.8)

Геометрично це означає, що множини

i X

можна помiстити в

рiзнi пiвпростори

pβ

= {x ∈ R

: p,x≥β},

−

pβ

= {x ∈ R

: p,x≤β},

якi породженi гiперплощиною

pβ

= {x ∈ R

: p,x = β},p=0.

При цьому кажуть, що гiперплощина H

pβ

роздiляє X

i X

,асамугi-

перплощину

pβ

називають роздiляючою. При власному роздiленнi ви-

ключається вироджений випадок, коли обидвi множини лежать у роздi-

ляючiй їх гiперплощинi. Сильне роздiлення означає, що множини знахо-

дяться на додатнiй вiдстанi вiд роздiляючої їх гiперплощини, а значить,

i одна вiд одної.

Теорема 1.3.8. (Теорема Мiнковського про роздiлення точки та мно-

жини.) Нехай

X ⊂ R

–замкнутаопукламножина,a –точкавR

що не належить

X. Тодi iснують такi p ∈ R

та β ∈ R,що

inf

x∈X

p,x >β>p,a. (1.3.9)

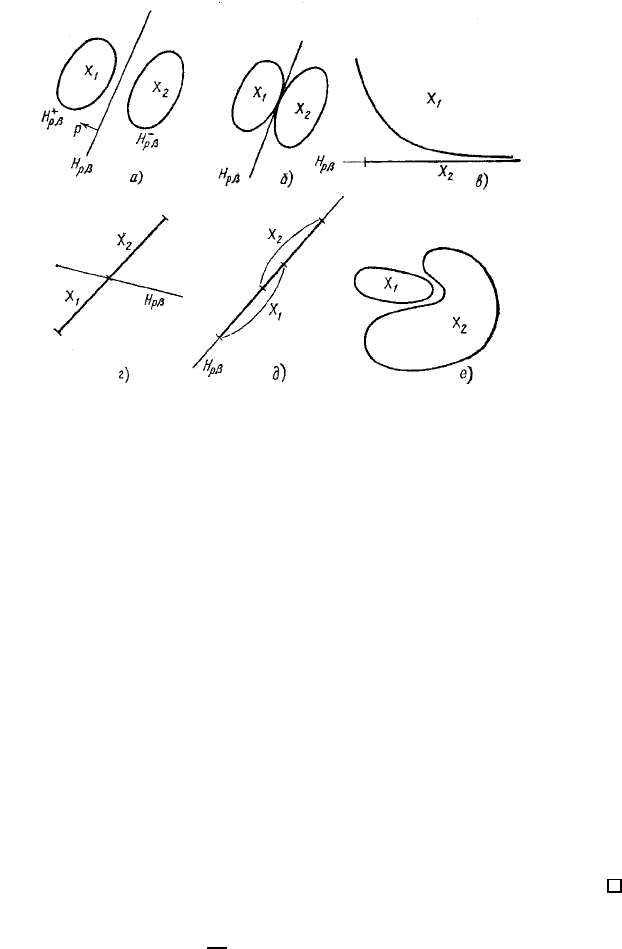
Рис. 1.3.4: Роздiлення двох множин.

Iнакше кажучи, стверджується iснування такої гiперплощини H

pβ

{x ∈ R

: p,x = β}, що множина X опиняється в одному з пiвпросторiв,

породжених

pβ

,аточкаa – всерединi iншого пiвпростору: X ⊂ H

pβ

{x ∈ R

: p,x≥β}, a ∈ int H

−

pβ

= {x ∈ R

: p,x <β}.Втойжечас

гiперплощина

pβ

= {x ∈ R

: p,x = p,a = β

}, що проходить через

точку

a, визначає пiвпростiр H

pβ

такий, що X ⊂ int H

pβ

Доведення. Нехай

(a) позначає проекцiю точки a на множину X.

Позначимо через

p = π

(a) − a.ГiперплощинаH

pβ

= {x ∈ R

: p,x =

p,a = β

} проходить через точку a i визначає пiвпростiр H

pβ

такий,

що

X ⊂ int H

pβ

. Дiйсно, iз спiввiдношення (1.3.5) отримаємо

π

(a) − a,x − a = p,x−p,a > 0 для всiх x ∈ X.

Отже,

p,x > p,a = β

для всiх x ∈ X.

Вибравши β зпромiжкуβ

= p,a <β<inf

x∈X

p,x,отримаємоспiв-

вiдношення (1.3.9).

Означення 1.3.8. Гiперплощина H

pβ

називається опорною до множини

X ⊂ R

вточцia ∈ ∂X = X \ intX,якщоX мiститься в одному з пiв-

Рис. 1.3.5: Опорнi гiперплощини.

просторiв, породжених цiєю гiперплощиною, а сама вона мiстить точку

a,тобто

p,x≥β = p,a при всiх x ∈ X. (1.3.10)

Означення 1.3.9. Гiперплощина

pβ

називається власне опорною до X

вточцia, якщо вона є опорною до X вточцia,аленемiститьповнiстю

X,тобто

p,ˆx >β при деякому ˆx ∈ X. (1.3.11)

Пiвпростiр, що породжений опорною (власне опорною) гiперплощи-

ною до

X вточцia, i такий, що мiстить X,такожназиваютьопорним

(власне опорним) до

X вточцia.

Теорема 1.3.9. Вбудь-якiйграничнiйточцi

a ∈ ∂X = X \int X опуклої

множини

X ⊂ R

iснує опорна гiперплощина.

Доведення. Умова

a ∈ ∂X = X \ int X означає, що iснує послiдовнiсть

точок

∈ R

\ X,k =1,2,...,яказбiгаєтьсядоa. Визначимо вектори

) − a

π

) − a



,k=1,2,...

Iз спiввiдношення (1.3.5) отримаємо, що

p

,x > p

 при всiх x ∈ X.

Оскiльки p

 =1,томожнавважати,щоp

→ p =0.Тодi,переходячи

до границi, отримаємо (1.3.10).

1.3.4. Крайнi точки опуклої множини

Означення 1.3.10. Точка опуклої множини X ⊂ R

називається край-

ньою (екстремальною),якщоїїнеможнаподатиувиглядi

x = λx

+(1−λ)x

, де x

∈ X, x

= x

, 0 <λ<1. (1.3.12)

Сукупнiсть усiх крайнiх точок множини

X позначимо через E(X).

Таким чином, точка

x є крайньою в X,якщоїїнеможнапомiстити

в середину вiдрiзка, кiнцi якого лежать в

X. Наприклад, у трикутника

крайнiми точками є його вершини, у променя – початок, у круга – всi

точки кола.

Наведемо лему, яка є корисним iнструментом для доведення насту-

пних основних теорем теорiї крайнiх точок. Саме формулювання леми

спирається на теорему про iснування опорної гiперплощини.

Лема 1.3.1. Нехай

X –замкнутаопукламножинавR

, H = H

pβ

–

власна опорна до

X вточцiˆx ∈ ∂X = X \int X гiперплощина, тобто

виконанi умови

p,x≥β = p,ˆx при всiх x ∈ X, (1.3.13)

p,¯x >β при деякому ¯x ∈ X. (1.3.14)

Покладемо

X = X ∩H

.Тодi:

1) будь-яка крайня точка в

єкрайньоюiвX,тобтоE(

X) ⊂ E(X);

2) dim

dim X.

Доведення. 1). Нехай

x ∈ E(

X),алеx ∈ E(X),тобтоx можна подати у

виглядi (1.3.12). Користуючись (1.3.13), отримаємо

β = p,x = λp,x

+(1− λ)p,x

≥λβ +(1− λ)β = β.

Звiдки p,x

 = p,x

 = β.Тобтоx

∈

X = X ∩H. Разом з (1.3.12) це

означає, що

x ∈ E(

X).Цясуперечнiстьдоводить,щоx ∈ E(X).Тобто

X) ⊂ E(X).

2). Покладемо

M = aﬀ X,

M =

aﬀ

.Тодi

M ⊂ M

M ⊂ H

,оскiльки

X ⊂ X

X ⊂ H

.Припустимо,що

M = M

.ТодiX ⊂ M =

M ⊂ H,тобто

β = p,x∀x ∈ X, що суперечить (1.3.14). Отже

M = M

.Паралельнi

пiдпростори

L = Lin X та

L =

Lin

пов’язанi такими самими спiввiд-

ношеннями

L ⊂ L

L = L

.ТомубазисL має принаймнi на один вектор

бiльше, нiж в

,тобтоdim

dim L. Але за означенням dim X = dim L,

dim

X =

dim

Теорема 1.3.10. (Теорема Мiнковського про опуклий компакт) Не-

хай

X – опуклий компакт (замкнута обмежена множина) в R

.Тодi

X = conv E(X),тобтоX спiвпадає з опуклою оболонкою множини

своїх крайнiх точок.

Доведення. Твердження доведемо методом математичної iндукцiї за роз-

мiрнiстю

X (розмiрнiстю простору, що мiстить X). Якщо dim X =1,то

X є вiдрiзком i теорема очевидна. Нехай твердження справедливе для

dim

X<mта dim X = m.НехайH = H

pβ

–власнаопорнадоX у деякiй

точцi

ˆx ∈ ∂X гiперплощина. Вiзьмемо

X = X ∩H

.Уданомувипадкуця

множина – опуклий компакт. При цьому dim

X<m

.Тодiзаприпущен-

ням iндукцiї

X =

conv E(

X).Маємоˆx ∈ conv E(

X).АлеE(

X) ⊂ E(X).

Тому

ˆx ∈ conv E(X).Отже,∂X ⊂ conv E(X).

Розглянемо тепер довiльну точку

ˆx ∈ IntX iвекторh ∈ Lin X.Пе-

ретин прямої

ˆxh

з X утворює вiдрiзок з кiнцями на границi X.Тобто

ˆxh

∩X = conv{x

}, x

∈ ∂X.Отжеˆx ∈ conv{x

}⊂conv (∂X) ⊂

conv (conv E(X)) = conv E(X).ТакимчиномIntX ⊂ conv E(X), X =

∂X∪

Int X ⊂ conv E(X). Обернене включення conv E(X) ⊂ X очевидне,

оскiльки

E(X) ⊂ X i X – опукла множина.

1.4. ГЕОМЕТРИЧНА IНТЕРПРЕТАЦIЯ ЗАДАЧI

ЛIНIЙНОГО ПРОГРАМУВАННЯ

Допустима множина задачi лiнiйного програмування (якщо вона не

порожня) – це многогранна множина. Отже, задача лiнiйного програму-

вання – це задача про вiдшукання мiнiмуму лiнiйної форми на много-

граннiй множинi. Покажемо, що з геометричної точки зору розв’язком

цiєї задачi є одна з вершин допустимої множини. Тим самим розв’язува-

ння зводиться до перебору скiнченної кiлькостi вершин.

Розглянемо задачу лiнiйного програмування у двовимiрному просторi.

Нехай обмеження задачi мають наступний вигляд:

+ a

≤ b

... ...

+ a

≤ b







(1.4.1)

Потрiбно знайти мiнiмум функцiї цiлi

(c,x)=c

+ c

Припустимо, що система (1.4.1) сумiсна i вiдповiдна їй многогранна мно-

жина

D обмежена, тобто є многокутником. Кожна з нерiвностей (1.4.1)

визначає пiвплощину разом iз граничною прямою

+ a

= b

,i=1,...,m,

а функцiя цiлi приймає однаковi значення C увсiхточкахпрямоїc

= C,деC – деяка константа. При змiнi (зменшеннi чи збiльшеннi

C) одержуємо сiм’ю паралельних прямих, якi називаються лiнiями рiвня