Моклячук М.П., Ямненко Р.Є. Лекції з теорії вибору та прийняття рішень (на укр. языке)
Подождите немного. Документ загружается.

(c,x)=
n
j=1
c
j
x
j
→ min . (1.5.6)
Означення 1.5.1. Допустимий розв’язок
x задачi лiнiйного програмува-
ння називається базисним (опорним), якщо система векторiв умов, що
вiдповiдає його додатнiм компонентам, лiнiйно незалежна.
Теорема 1.5.1. Допустимий розв’язок
x задачi лiнiйного програмува-
ння є вершиною допустимої областi (многогранника розв’язкiв) тодi
i тiльки тодi, коли вiн є базисним.
Доведення. 1). Достатнiсть. Нехай
x є базисним розв’язком задачi лiнiй-
ного програмування. Можна припустити, що першi компоненти розв’язку
x вiдмiннi вiд нуля, a iншi – нулi, тобто
x =(x
1
,...,x
k
,0,...,0).
За означенням
k
j=1
x
j
A
j
= b (1.5.7)
iсистемавекторiв
A
1
,...,A
k
лiнiйно незалежна. Покажемо, що x євер-
шиною многогранника розв’язкiв. Припустимо протилежне, тобто що
x
не є вершиною i може бути представлений у виглядi
x = λx
1
+(1−λ)x
2
, 0 <λ<1,
де x
1
,x
2
– двi рiзнi точки многогранника. В силу того, що 0 <λ<1,
точки
x
1
,x
2
матимуть вигляд
x
1
=(x
1
1
,...,x
1
k
,0,...,0),
x
2
=(x
2
1
,...,x
2
k
,0,...,0).
Оскiльки x
1
,x
2
– це допустимi розв’язки, то
k
j=1
x
1
j
A
j
= b,
k
j=1
x
2
j
A
j
= b. (1.5.8)
Вiднiмаючи вiд першого iз спiввiдношень друге, одержимо
k
j=1
(x
1
j
− x
2
j
)A
j
=0.
З лiнiйної незалежностi векторiв A
1
,...,A
k
випливає, що x
1
= x
2
.Це
суперечить тому, що
x
1
= x
2
.Томуx євершиною.
2) Необхiднiсть. Нехай
x =(x
1
,...,x
k
,0,...,0)
41

є вершиною допустимої областi. Покажемо, що x є базисним розв’язком.
Дляцьогодоситьцоказати,щосистемавекторiв
A
1
,..., A
k
лiнiйно
незалежна. Припустимо протилежне. Тодi iснують
α
j
,щоневсiрiвнi
нулю i такi, що
k
j=1
α
j
A
j
=0. (1.5.9)
Оскiльки
x є допустимим розв’язком, то
k
j=1
x
j
A
j
= b. (1.5.10)
Виходячи з рiвностей (1.5.9), (1.5.10), розглянемо такi вирази для до-
вiльного
ε>0:
k
j=1
(x
j
+ εα
j
)A
j
= b,
k
j=1
(x
j
− εα
j
)A
j
= b.
Можна пiдiбрати таке ε>0,щобточки
x
1
=(x
1
+ εα
1
,...,x
k
+ εα
k
,0 ...,0),
x
2
=(x
1
− εα
1
,...,x
k
− εα
k
,0 ...,0)
(1.5.11)
мали додатнi компоненти, тобто були допустимими розв’язками задачi
(1.5.4)–(1.5.6). З (1.5.11) випливає, що
x =
1
2
x
1
+ x
2
,
тобто x не є вершиною. Отримана суперечнiсть доводить теорему.
Отже, якщо додатнiм компонентам деякого допустимого розв’язку
вiдповiдають лiнiйно незалежнi вектори умов, тo цей допустимий розв’я-
зок є вершиною многогранника допустимих розв’язкiв.
Виходячи з теореми, можна було б запропонувати такий шлях розв’я-
зання задачi лiнiйного програмування: вибирається довiльна лiнiйно не-
залежна система векторiв умов, компоненти
x
j
,щоневiдповiдаютьцим
векторам, покладаються рiвними нулю; знаходиться розв’язок отриманої
при цьому системи (1.5.4). Якщо вiн задовольняє умову невiд’ємностi,
то це вершина допустимої областi. За знайденим розв’язком обчислю-
ється i запам’ятовується значення цiльової функцiї. Потiм вибирається
iнша лiнiйно незалежна система векторiв умов i т.д. Теоретично таким
шляхом можна одержати розв’язок задачi лiнiйного програмування, виб-
равши серед знайдених значень функцiї цiлi мiнiмальне. У запропонова-
42
ному пiдходi вiдсутня цiлеспрямованiсть у переборi вершин допустимої
областi i реалiзацiя його практично неможлива.
У теорiї лiнiйного програмування здiйснюється цiлеспрямований пе-
ребiр сусiднiх вершин многогранника розв’язкiв: виходять з деякої поча-
ткової вершини, переходячи у сусiднi вершини так, щоб у новiй вершинi
значення цiльової функцiї цiлi було менше.
1.6. КАНОНIЧНА ФОРМА ЗАДАЧI ЛIНIЙНОГО
ПРОГРАМУВАННЯ. ПЕРЕБIР ВЕРШИН МЕТОДОМ
ВИКЛЮЧЕННЯ ЖОРДАНА-ГАУССА
Оскiльки розв’язання задачi лiнiйного програмування зводиться до
перебору вершин, то виникають питання: як знайти початкову верши-
ну i як перейти до iншої вершини? Розглянемо канонiчну форму задачi
лiнiйного програмування i метод виключення Жордана–Гаусса.
Система рiвнянь (1.5.1) називається записаною в канонiчнiй формi,
якщо:
• 1) її правi частини невiд’ємнi;
• 2) для кожного з рiвнянь є змiнна з коефiцiєнтом 1 у цьому рiв-
няннi i коефiцiєнтом 0 у всiх iнших рiвняннях.
При цьому говорять, що вiдповiдна задача лiнiйного програмування
має канонiчну форму.
Для простоти припустимо, що система (1.5.1) записана у виглядi
x
1
+ α
1m+1
x
m+1
+ ... +α
1k
x
k
+ ... +α
1n
x
n
= β
1
,
... ... ... ... ...
x
i
+ α
im+1
x
m+1
+ ... +α
ik
x
k
+ ... +α
in
x
n
= β
i
,
... ... ... ... ...
x
l
+ α
lm+1
x
m+1
+ ... +α
lk
x
k
+ ... +α
ln
x
n
= β
l
,
... ... ... ... ...
x
m
+ α
mm+1
x
m+1
+ ... +α
mk
x
k
+ ... +α
mn
x
n
= β
m
,
(1.6.1)
де β
i
≥ 0. Змiннi x
1
,...,x
m
називаються базисними,iншi–вiльними
(позабазисними).
Канонiчна форма задачi лiнiйного програмування зручна тим, що лег-
ко знаходиться початкова вершина допустимої областi. Дiйсно, точка
(β
1
,...,β
m
,0,...,0)
є вершиною допустимої областi, тому що вектори умов, якi вiдповiдають
x
1
,...,x
m
, є лiнiйно незалежними.
43
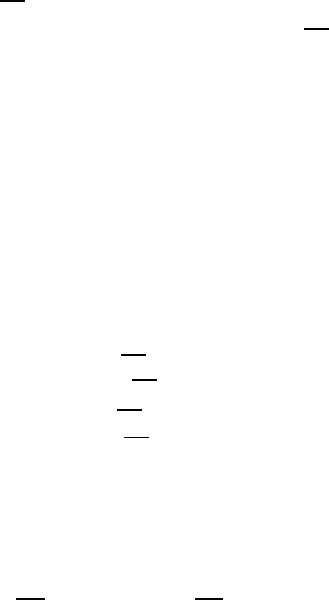
Вiд задачi в стандартнiй формi легко перейти до рiвносильної задачi
в канонiчнiй формi, вводячи штучнi змiннi. Множенням, якщо потрiбно,
на
−1 обох частин рiвнянь (1.5.1) можна домогтися того, що їх правi
частини стануть невiд’ємнми. Потiм у кожне рiвняння
i =1,...,m, вво-
диться своя змiнна
x
n+i
, а щоб в оптимальному планi цi змiннi були
рiвнi 0, одночасно з великим коефiцiєнтом
M вони вводяться у функцiю
цiлi. Цей прийом одержав назву
M-методу.
Перейдемо вiд системи в канонiчнiй формi (1.6.1) до еквiвалентної
їй системi, застосовуючи метод виключення Жордана–Гаусса. Для цьо-
го виключимо з усiх рiвнянь, крiм
l-го, змiнну x
k
шляхом множен-
ня
l-го рiвняння на
α
ik
α
lk
i вiднiмання результату вiд i-го рiвняння i =
1,...,l − 1,l +1,...,m
.Помножившиl-е рiвняння на
1
α
lk
,миодержимо
канонiчну систему, що вiдрiзняється вiд попередньої тiльки тим, що в
l-ому рiвняннi змiнною з коефiцiєнтом 1 буде x
k
,анеx
l
.Цясистема
має такий вигляд:
x
1
+ α
1l
x
l
+ α
1m+1
x
m+1
+ ... +α
1k
x
k
+ ... +α
1n
x
n
= β
1
,
... ... ... ... ...
x
i
+ α
il
x
l
+ α
im+1
x
m+1
+ ... +α
ik
x
k
+ ... +α
in
x
n
= β
i
,
... ... ... ... ...
α
ll
x
l
+ α
lm+1
x
m+1
+ ... +α
lk
x
k
+ ... +α
ln
x
n
= β
l
,
... ... ... ... ...
x
m
+ α
ml
x
l
+ α
mm+1
x
m+1
+ ... +α
mj
x
j
+ ... +α
mn
x
n
= β
m
,
(1.6.2)
де
α
ij
=
α
ij
α
lk
,i= l,
α
ij
−
α
lj
α
lk
α
ik
,i= l,
β
i
=
β
i
α
lk
,i= l,
β
i
−
β
l
α
lk
α
ik
,i= l.
(1.6.3)
Для того, щоб нова канонiчна система визначала вершину много-
гранника розв’язкiв, її правi частини повиннi бути невiд’ємними. Тому
потрiбно вибирати такi рядок i стовпець, щоб виконувалися наступнi двi
умови:
1)
β
l
α
lk
≥ 0; 2) β
i
−
β
l
α
lk
α
ik
≥ 0.
Якщо вибрати ту змiнну x
k
, для якої принаймнi одна компонента вiдпо-
вiдного їй вектора умов строго додатна
(α
lk
> 0),тотимсамимумова1)
буде виконана. Крiм цього, повинна виконуватися умова 2).
Якщо
α
ik
< 0,тоумова2)такожвиконується.
44

Якщо ж α
ik
> 0,тоl потрiбно вибрати так, щоб
β
i
α
ik
≥
β
l
α
lk
.
Отже, l повинно бути таким, щоб
β
l
α
lk
=min
i:α
ik
>0
β
i
α
ik
=: θ. (1.6.4)
Отриманий результат можна сформулювати у виглядi такого правила:
Вiд канонiчної форми рiвнянь (1.6.1), яка визначає деяку вер-
шину многогранника розв’язкiв, до канонiчної форми (1.6.2), яка
визначає наступну вершину многранника розв’язкiв, можна пере-
йти так: треба взяти небазисну змiнну
x
k
,якiйвiдповiдаєвектор
умов принаймнi з однiєю додатною компонентою; вибрати
l-е рiв-
няння з умови (1.6.4); потiм виключити змiнну
x
k
з усiх рiвнянь,
крiм
l-го; в результатi одержимо нову канонiчну систему, яка ви-
значає нову вершину допустимой областi.
Виникає природне запитанння: чи не можна вибрати таку вершину,
щоб значенння функцiї цiлi у цiй вершинi було менше, нiж у початковiй.
У початковiй вершинi
x
0
=(β
1
,...,β
m
,0,...,0) значення функцiї цiлi
дорiвнює:
(c,x
0
)=
m
i=1
c
i
β
i
.
Нова вершина має координати
x
=(β
1
− θα
1k
,...,β
l−1
− θα
l−1,k
,0,β
l+1
− θα
l+1,k
,...,
β
m
− θα
mk
,0,...,0,θ,0,...,0) =
=(β
1
− θα
1k
,...,β
l−1
− θα
l−1,k
,β
l
− θα
l,k
,β
l+1
− θα
l+1,k
,...,
β
m
− θα
mk
,0,...,0,θ,0,...,0),
тому що β
l
− θα
l,k
=0. Обчислимо значення функцiї цiлi (c,x) уновiй
вершинi
(c,x
)=
m
i=1
c
i
(β
i
− θα
ik
)+θc
k
=(c,x
0
)+θ(c
k
− z
k
), (1.6.5)
z
k
=
m
i=1
c
i
α
ik
. (1.6.6)
З (1.6.5) випливає, що якщо вибрати таке
x
k
,приякому∆
k
= c
k
−z
k
< 0,
то значення функцiї цiлi в новiй вершинi буде менше, нiж у початковiй.
45

Отже, ми розглянули всi питання, що необхiднi для описання симп-
лекс-методу – одного з основних методiв розв’язування задач лiнiйного
програмування.
1.7. СИМПЛЕКС-МЕТОД. КРИТЕРIЙ ОПТИМАЛЬНОСТI
The tremendous power of the simplex method
is a constant surprise to me.
D.Dantzig
Симплекс-метод застосовується для розв’язування задач лiнiйного
програмування тодi, коли задача лiнiйного програмування записана в
канонiчнiй формi. У цьому випадку автоматично знаходиться початко-
ва вершина допустимої областi, а потiм здiйснюється цiлеспрямований
перебiр вершин многокутника розв’язкiв. З цiєю метою для кожної з
позабазисних змiнних, користуючись (1.6.6), пiдраховуються величини
c
k
− z
k
,якiназиваютьсявiдносними оцiнками. Вибирається змiнна x
k
,
для якої
c
k
− z
k
< 0 i, крiм того, вектор умов, що вiдповiдає x
k
,має
принаймнi одну додатну компоненту. Для кожного
i обчислюємо
β
i
α
ik
i
вибираємо те рiвняння, де це вiдношення мiнiмальне. Нехай це буде
l-е
рiвняння. Потiм за методом Жордана–Гаусса, використовуючи формули
(1.6.3), виключаємо змiнну
x
k
iз усiх рiвнянь, крiм l-го. В результатi
перейдемо до задачi лiнiйного програмування в канонiчнiй формi, що
визначає нову вершину многогранника розв’язкiв. Як випливає з попе-
реднього параграфа, значення функцiї цiлi в новiй вершинi буде менше,
нiж у попереднiй. Далi виконуємо аналогiчний цикл операцiй, що нази-
вається iтерацiєю. Цей процес продовжується доти, поки вiдноснi оцiнки
позабазисних змiнних не стануть додатними. У цьому випадку перехiд
до нової вершини недоцiльний. Покажемо, що тодi задача лiнiйного про-
грамування розв’язана.
Теорема 1.7.1. (Критерiй оптимальностi.) Якщо для деякого бази-
сного розв’язку
x =(x
1
, ..., x
n
) справедливi нерiвностi
∆
k
= c
k
− z
k
≥ 0,k=1,...,n, (1.7.1)
то
x є розв’язком задачi лiнiйного програмування.
Доведення. Позначимо вектори умов початкової системи рiвнянь через
A
1
,...,A
n
,b i нехай базисному розв’язку x вiдповiдає канонiчна система
(1.6.1). Матрицi умов цих систем, тобто матрицi, складенi з векторiв
умов початкової i кiнцевої системи, що вiдповiдає
x,маютьвигляд
A =(A
1
,...,A
m
,A
m+1
,...,A
n
),α=(I,α
m+1
,...,α
n
),
46

де I – одинична матриця розмiрностi m × m,
α
j
=(α
1j
,...,α
mj
)
,j= m +1,...,n.
Позначимо через f (x) значення лiнiйної форми (c,x),щовiдповiдаєроз-
в’язку
x =(x
1
,...,x
n
).Нехайy =(y
1
,...,y
n
) – довiльний допустимий
розв’язок, тобто
n
j=1
y
j
A
j
= b. (1.7.2)
Нехай
f(y) – значення лiнiйної форми, що вiдповiдає розв’язку y =
(y
1
,...,y
n
). Покажемо, що за умови (1.7.1) f (x) ≤ f (y).Використовуючи
(1.7.1), (1.6.6) i змiнюючи порядок додавання, одержимо
f(y)=
n
j=1
c
j
y
j
≥
n
j=1
z
j
y
j
=
n
j=1
m
i=1
c
i
α
ij
y
j
= (1.7.3)
=
m
i=1
n
j=1
α
ij
y
j
c
i
. (1.7.4)
Покажемо, що
n
j=1
α
ij
y
j
= x
i
.
Позначимо через B матрицю, складену з векторiв A
1
,...,A
m
,щонази-
вається базисом, тобто
B =(A
1
,...,A
m
).Тодi
α = B
−1
A, aбo α
j
= B
−1
A
j
,j=1,...,n.
Отже, A
j
= Bα
j
.Цеможназаписатищетак:
A
j
=
m
i=1
α
ij
A
i
,j=1,...,n. (1.7.5)
Пiдставляючи це значення в рiвнiсть (1.7.2), одержуємо
b =
n
j=1
y
j
A
j
=
n
j=1
y
j
m
i=1
α
ij
A
i
=
m
i=1
n
j=1
α
ij
y
j
A
i
.
Оскiльки x задовольняє початкову систему рiвнянь, то
b =
m
i=1
x
i
A
i
,
причому система векторiв A
1
,...,A
m
лiнiйно незалежна. Тому
n
j=1
α
ij
y
j
= x
i
i з (1.7.4) одержуємо f(y) ≥ f (x), що i потрiбно довести.
47

Ознаки необмеженостi знизу цiльової функцiї на допустимiй множинi
дає наступна теорема.
Теорема 1.7.2. Якщо для деякого базисного розв’язку
x =(x
1
, ..., x
n
)
iснує принаймнi одна позабазисна змiнна x
k
,дляякої∆
k
= c
k
−z
k
< 0
i α
ik
≤ 0,i =1,...,m, то функцiя цiлi задачi лiнiйного програмування
необмежена знизу на допустимiй множинi.
Доведення. Нехай
x =(x
1
,...,x
m
,0 ...,0) – базисний розв’язок, а x
k
– позабазисна змiнна, що задовольняює умови теореми. Покажемо, що
вектор
x
=(x
1
− θα
1k
,...,x
m
− θα
mk
,0,...,0,θ,0 ...,0),
де x
k
= θ,прибудь-якомуθ>0 є допустимим. Дiйсно, компоненти
вектора
x
невiд’ємнi. Крiм того, x
є допустимим розв’язком задачi лi-
нiйного програмування, оскiльки з рiвностi (1.7.5) маємо
m
i=1
(x
i
− θα
ik
)A
i
+ θA
k
=
=
m
i=1
x
i
A
i
− θ
m
i=1
α
ik
A
i
+ θA
k
= b − θA
k
+ θA
k
= b.
Знайдемо значення функцiї цiлi, що вiдповiдає допустимому вектору x
:
(c,x
)=
m
i=1
c
i
(x
i
− θα
ik
)+θc
k
=
m
i=1
c
i
x
i
+ θ(c
k
− z
k
).
Оскiльки за умовою маємо ∆
k
= c
k
− z
k
< 0, то, взявши досить велике
додатне число
θ, значення (c,x
) можна зробити як завгодно малим, що i
доводить теорему.
Табл.1.7.1
48

Базис x
1
... x
m
x
m+1
... x
k
... x
n
x
1
1 ... 0 α
1m+1
... α
1k
... α
1n
β
1
... ... ... ... ... ... ... ... ... ...
x
l
0 ... 0 α
lm+1
... α
lk
... α
ln
β
l
... ... ... ... ... ... ... ... ... ...
x
m
0 ... 1 α
mm+1
... α
mk
... α
mn
β
m
F c
1
... c
m
c
m+1
... c
k
... c
n
c
0
Z z
1
... z
m
z
m+1
... z
k
... z
n
∆ ∆
1
... ∆
m
∆
m+1
... ∆
k
... ∆
n
Зведемо всi коефiцiєнти при вiльних змiнних з (1.6.1) та вiльнi члени
зформи
F у симплекс-таблицю (див. таблицю 1.7.1). Кожен рядок цiєї
таблицi вiдповiдає рiвнянню, яке виражає базиснi змiннi через вiльнi,
останнi три рядки вiдповiдають формi
F , обчисленим коефiцiєнтам z
i
та ∆
i
. Кожен стовпець вiдповiдає деякiй вiльнiй змiннiй, останнiй –
вiльним членам. Коефiцiєнт
α
lk
,дляякого∆
k
< 0 та виконується умова
(1.6.4), будемо називати генеральним елементом,усимплекс-таблицi
його пiдкреслено.
На практицi бiльш зручно користуватись формою
F ,яказалежить
лише вiд вiльних змiнних, тобто коефiцiєнти при базисних змiнних
c
1
= ... = c
m
=0, причому у таблицю записувати коефiцiєнти −c
i
,
i =1,...,n. При переходi до нового базису коефiцiєнти c
i
обчислюються
за правилом, аналогiчним формулам (1.6.3):
c
i
=
c
i
+
α
li
α
lk
c
k
при 1 ≤ i ≤ n;
c
0
−
β
l
α
lk
c
k
для i =0
(1.7.6)
або, що те саме,
(−c
i
)=(−c
i
) −
α
lj
α
lk
c
k
для 1 ≤ i ≤ n. (1.7.7)
Табл.1.7.2
49
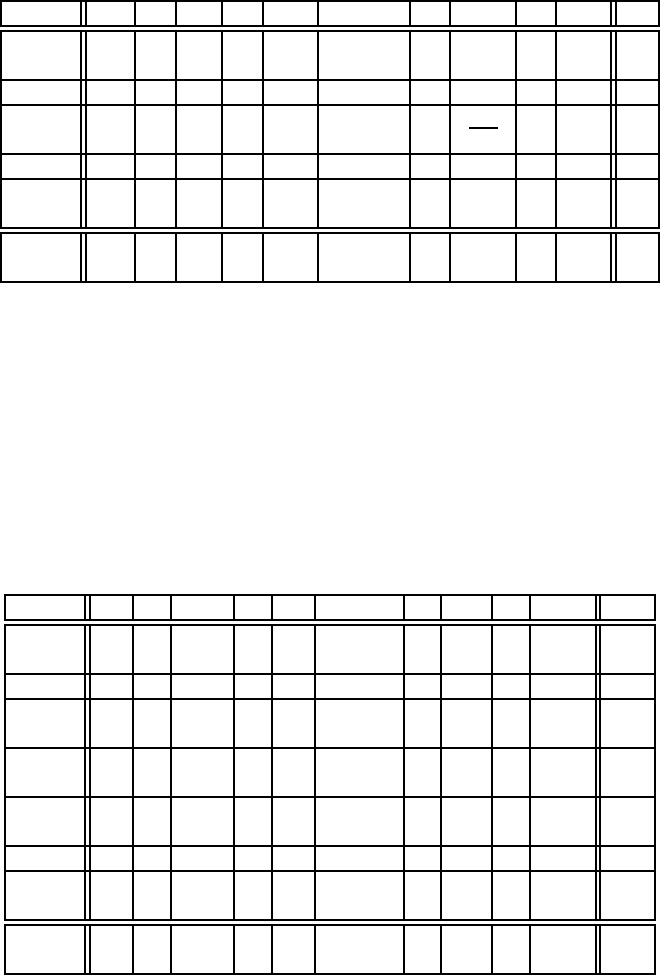
Базис x
1
... x
l
... x
m
x
m+1
... x
k
... x
n
x
1
1 ... 0 ... 0 α
1m+1
... α
1k
... α
1n
β
1
... ... ... ... ... ... ... ... ... ... ... ...
x
l
0 ... 1 ... 0 α
lm+1
... α
lk
... α
ln
β
l
... ... ... ... ... ... ... ... ... ... ... ...
x
m
0 ... 0 ... 1 α
mm+1
... α
mk
... α
mn
β
m
F 0 ... 0 ... 0 −c
m+1
... −c
k
... −c
n
c
0
Згiдно зi сказаним у параграфах § 1.6-1.7 наведемо наступний алго-
ритм роботи iз симплекс-таблицею.
1. Знаходимо в останньому рядку симплекс-таблицi 1.7.2 який-небудь
додатний елемент, наприклад, −c
k
(тобто c
k
< 0; c
0
не розглядається).
Якщо в останньому рядку немає додатних елементiв, то записаний у цiй
симплекс-таблицi базисний розв’язок є оптимальним.
2. Вибираємо генеральний елемент α
lk
> 0 за критерiєм (1.6.4).
3. Вiд таблицi 1.7.2, використовуючи формули (1.6.3) i (1.7.6), перехо-
димо до таблицi 1.7.3, що вiдповiдає новому набору вiльних змiнних.
4. Якщо необхiдно, повторити послiдовнiсть крокiв 1-3.
Табл.1.7.3
Базис x
1
... x
l
... x
m
x
m+1
... x
k
... x
n
x
1
1 ... α
1l
... 0 α
1m+1
... 0 ... α
1n
β
1
... ... ... ... ... ... ... ... ... ... ... ...
x
l−1
0 ... α
l−1l
... 0 α
l−1m+1
... 0 ... α
l−1n
β
l−1
x
k
0 ... α
ll
... 0 α
lm+1
... 1 ... α
ln
β
l
x
l+1
0 ... α
l+1l
... 0 α
l+1m+1
... 0 ... α
l+1n
β
l+1
... ... ... ... ... ... ... ... ... ... ... ...
x
m
0 ... α
ml
... 1 α
mm+1
... 0 ... α
mn
β
m
F 0 ... − c
l
... 0 −c
m+1
... 0 ... −c
n
c
0
50
