Моклячук М.П., Ямненко Р.Є. Лекції з теорії вибору та прийняття рішень (на укр. языке)
Подождите немного. Документ загружается.

функцiї c
1
x
1
+ c
2
x
2
. Нас цiкавлять тi точки многокутника D,якiнале-
жать лiнiї рiвня з найменшим значенням
C.Якщоперемiщуватипряму
c
11
+ c
2
x
2
= C унапрямкуїїнормалic =(c
1
,c
2
), то значення C буде
збiльшуватись. Значення
C буде зменшуватись, якщо перемiщувати пря-
муунапрямку
−c. Виберемо досить велике C i будемо перемiщувати
пряму
c
1
x
1
+ c
2
x
2
= C унапрямку−c. При цьому лiнiї рiвня (c,x)=C
спочатку можуть не мати спiльних точок з многокутником D,апотiм
почнуть наближатися до нього. При деякому
C пряма (c,x)=C вперше
торкнеться многокутника
D, потiм перетне його i, нарештi, наступить
момент, коли вона торкнеться многокутника востаннє. Значення функцiї
цiлi в цей момент мiнiмальне. Розв’язок задачi iснує.
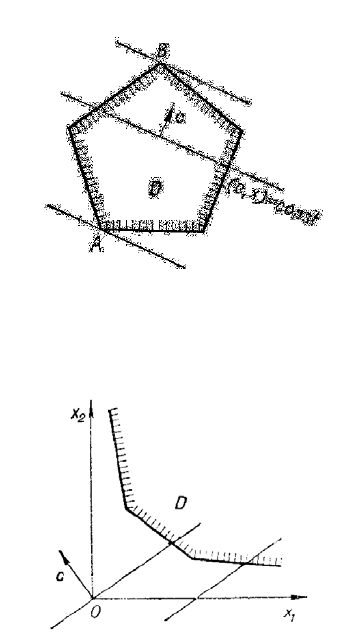
Рис. 1.4.1: Множина D обмежена. Розв’язок задачi iснує.
Рис. 1.4.2: Множина D необмежена. Розв’язок задачi не iснує.
21
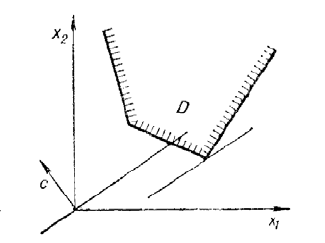
Рис. 1.4.3: Множина D необмежена. Розв’язок задачi iснує.
Якщо ж многокутник необмежений, то може бути два випадки:
• 1) пряма c
1
x
1
+ c
2
x
2
= C, перемiщаючись у напрямку −c,весьчас
перетинає многокутник
D; у цьому випадку лiнiйна форма необме-
жена на допустимiй областi i її мiнiмум дорiвнює
−∞.
• 2) в результатi перемiщення вздовж напрямку −c пряма c
1
x
1
+
c
2
x
2
= C стає опорною до многокутника D.
Геометрична iнтерпретацiя пiдказує нам, що розв’язком задачi лiнiй-
ного програмування може бути крайня точка допустимої множини. До-
ведемо строго це положення. Розглянемо типовий для практичних задач
випадок, коли допустима множина задачi лiнiйного програмування є мно-
гогранником. Крайнi точки многогранника називаються його вершинами.
Теорема 1.4.1. Нехай допустима множина
D задачi лiнiйного про-
грамування (1.2.1) – (1.2.5) є многогранником. Тодi:
• 1) функцiя цiлi досягає свого мiнiмуму у вершинi многогранника;
• 2) якщо лiнiйна форма приймає мiнiмальне значення бiльш, нiж
в однiй точцi, то вона досягає таке ж значення в будь-якiй
точцi, що є їх опуклою комбiнацiєю.
Доведення. Нехай
x
1
,x
2
,...,x
p
– вершини многогранника D iнехайx
∗
– розв’язок задачi (1.2.1) – (1.2.5), тобто (c,x
∗
) ≤ (c,x) для всiх x ∈
D
.Якщоx
∗
– вершина многогранника D,топершачастинатеореми
доведена. Якщо ж
x
∗
не вершина многогранника розв’язкiв, то x
∗
може
бути записана як опукла комбiнацiя його вершин, тобто
x
∗
=
p
i=1
λ
i
x
i
,λ
i
≥ 0,i=1,...,p,
p
i=1
λ
i
=1.
22

В силу лiнiйностi функцiї (c,x) маємо
(c,x
∗
)=
p
i=1
λ
i
(c,x
i
) ≥ (c,x
k
),
де
(c,x
k
)= min
1≤i≤p
(c,x
i
).
За припущенням x
∗
є оптимальним розв’язком. Отже (c,x
∗
)=(c,x
k
),
тобто iснує вершина
x
k
, у якiй лiнiйна форма приймає мiнiмальне зна-
чення.
Доведемо другу частину теореми. Нехай
(c,x) приймає мiнiмальне
значення в точках
x
1
,x
2
,...,x
s
,тобто
(c,x
j
)=
f, j =1,...,s.
Вiзьмемо довiльну опуклу комбiнацiю цих точок
x =
s
i=1
λ
i
x
i
,λ
i
≥ 0,i=1,...,s,
s
i=1
λ
i
=1.
Тодi
(c,x)=
c,
s
i=1
λ
i
x
i
=
s
i=1
λ
i
(c,x
i
)=
f
s
i=1
λ
i
=
f.
Отже, цiльова функцiя (c,x) досягає мiнiмального значення
f
удовiльнiй
точцi
x множини з вершинами x
1
,x
2
,...,x
s
.
Ми приходимо до висновку, що для того, щоб розв’язати задачу лiнiй-
ного програмування, досить зробити перебiр крайнiх точок многогранни-
ка розв’язкiв.
1.4.1. Задача про розподiл ресурсiв
Обмеження i форма F
1
у цiй задачi (див. §1.1, стор. 6) є такими:
x
1
≥ 0,
x
2
≥ 0,
19 − 2x
1
− 3x
2
≥ 0,
13 − 2x
1
− x
2
≥ 0,
15 − 3x
2
≥ 0,
18 − 3x
1
≥ 0,
F
1
= −7x
1
− 5x
2
.
Визначимо на площинi прямокутну декартову систему координат Ox
1
x
2
.
Вiдомо, що геометричне мiсце точок на площинi, координати яких задо-
вольняють системi лiнiйних нерiвностей, утворюють опуклий многоку-
23
тник. Цей многокутник називають многокутником розв’язкiв даної си-
стеми нерiвностей. Сторони цього многокутника розташованi на прямих,
рiвняння яких можна отримати, замiнивши у нерiвностях системи знаки
знаки нерiвностей на точнi рiвностi. Сам цей многокутник є перетином
пiвплощин, на якi дiлить площина кожна iз вказаних прямих. У нашому
випадку такими прямими є
x
1
=0, (I)
x
2
=0, (II)
19 − 2x
1
− 3x
2
=0, (III)
13 − 2x
1
− x
2
=0, (IV )
15 − 3x
2
=0, (V )
18 − 3x
1
=0. (VI)
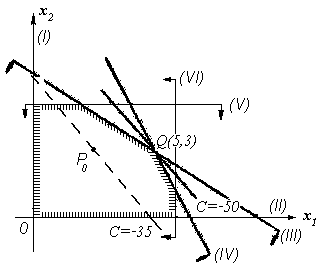
Накреслимо цi прямi (рис. 1.4.4); стрiлки вказують, якi пiвплощини
у перетинi дають многокутник розв’язкiв.
Рис. 1.4.4: Геометрична iнтерпретацiя задачi про розподiл ресурсiв.
Поряд з цим розглянемо форму F
1
= −7x
1
− 5x
2
. Очевидно, вона
є лiнiйною функцiєю координат
(x
1
,x
2
) точки на площинi. Поставимо
таке питання: як розташовуються на площинi тi точки, у яких форма
F
приймає одне i те ж значення C? Для вiдповiдi на це питання достатньо
форму
F прирiвняти до C i розглянути отримане рiвняння
−7x
1
− 5x
2
= C. (1.4.2)
Це рiвняння визначає на площинi деяку пряму. Вона i є шуканим гео-
метричним мiсцем точок, в яких
F
1
набуває дане значення C. Змiнюючи
значення
C, отримаємо рiзнi прямi, але всi вони паралельнi мiж собою,
тобто утворюють сiм’ю паралельних прямих. При переходi вiд однiєї пря-
мої до iншої значення форми
F
1
змiнюється. На рис. 1.4.5 показанi пря-
24
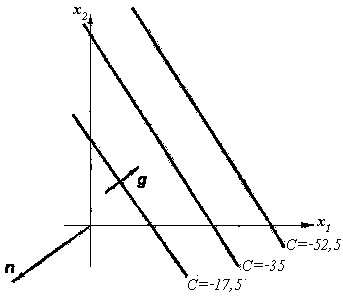
Рис. 1.4.5: Прямi форми F
1
при рiзних значеннях C.
мi, якi вiдповiдають значенням C = −17,5; C = −35; C = −52,5.Вектор
g вказує напрямок, рухаючись вздовж якого, ми переходимо вiд бiль-
ших значень форми до менших. З курсу аналiтичної геометрiї вiдомо,
що коефiцiєнти при змiнних у рiвняннi прямої є проекцiями вектора
n,
перпендикулярного до прямої. У нашому випадку
n = {−7; −5}.Можна
спостерiгати, що напрямок зменшення значень форми
F
1
протилежний
напрямку вектора
n.
Повернемось знову до рис. 1.4.4. Розглянемо довiльну точку
P
0
(x
(0)
1
,
x
(0)
2
) многокутника розв’язкiв. Через цю точку проходить пряма сiм’ї
(1.4.2). Уздовж всiєї цiєї прямої форма
F
1
набуває таке ж значення, як i
уточцi
P
0
,тобтоC
0
= −7x
(0)
1
− 5x
(0)
2
.
На рис. 1.4.4 пунктиром показана пряма, що вiдповiдає значенню
C = −35.Очевидно,щоточкаP
0
не є оптимальним розв’язком зада-
чi. Дiйсно, всерединi многокутника розв’язкiв можна знайти точки, для
яких значення форми менше, нiж
C
0
. Для цього досить перейти в на-
прямку вектора
g вiд прямої C
0
до iншої, паралельнiй їй прямiй сiм’ї
(1.4.2), яка ще перетинає многокутник розв’язкiв. Тепер має стати зро-
зумiлим, що оптимальний розв’язок визначається точкою
Q(5,3),анай-
менше значення форми
F
1
дорiвнює
F
1min
= −7 · 5 − 5 · 3=−50.
Отже, оптимальний розв’язок задачi знайдено:
x
1
=5,x
2
=3.
Якщо згадати умову цiєї задачi (§1.1, стор. 6), то ми бачимо, що для
найбiльш рацiонального плану використання сировини, що гарантувати-
25

ме пiдприємству найбiльший прибуток, потрiбно випускати 5 одиниць
продукцiї виду
P
1
i 3 одиницi виду P
2
, причому максимальний прибуток
складе
F
max
=50. Вiдмiтимо, що при цьому сировина видiв R
1
i R
2
використовується повнiстю, а R
3
i R
4
–неповнiстю.
1.4.2. Задача про перевезення
Для визначеностi надамо вiдомим за умовою задачi 1.1.1 (див. §1.1.1,
стор. 8) величинам деякi числовi значення i зведемо їх в таблицю 1.4.1.
Табл.1.4.1
B
1
B
2
B
3
Запаси
A
1
4 9 3 20
A
2
4 8 1 30
Потреби 10 30 10 50
Тодi система обмежень i форма F матимуть наступний вигляд:
x
11
+ x
21
=10,
x
12
+ x
22
=30,
x
13
+ x
23
=10,
x
11
+ x
12
+ x
13
=20,
x
21
+ x
22
+ x
23
=30,
F =4x
11
+9x
12
+3x
13
+4x
21
+8x
22
+ x
23
.
Випишемо матрицю системи:
100100
010010
001001
111000
000111
.........
x
11
x
12
x
13
x
21
x
22
x
23
(над x
ij
виписанi коефiцiєнти, з якими цi невiдомi входять у вiдповiднi
рiвняння).
Пiдрахуємо ранг
r цiєїматрицi.Дляцьогододамодопершогорядка
другий i третiй i вiднiмемо четвертий та п’ятий; отримаємо рядок з одних
нулiв. Тому
r<5. Легко перевiрити, що мiнор цiєї матрицi, отриманий
першими чотирма рядками i стовпчиками, вiдмiнний вiд нуля. Таким
чином,
r =4. Пiдрахуємо тепер ранг r
розширеної матрицi:
26
10010010
01001030
00100110
11100020
00011130
.
Якщо i в цiй матрицi до першого рядка додати другий i третiй, а потiм
вiдняти четвертий i п’ятий, то знову отримаємо рядок з одних нулiв.
Тому
r
< 5, але так як ранг розширеної матрицi не менший рангу
основної, тому
r
=4.
Зауваження. Якщо виконується умова
m
i=1
a
i
=
n
j=1
b
j
, (1.4.3)
то система (1.1.1) завжди сумiсна. Дiйсно, якщо не зважати на вар-
тiсть перевезень (тобто не домагатися мiнiмiзацiї форми
F ), то цiлком
очевидно, що iснує багато способiв органiзувати необхiднi перевезення.
Бiльш того, якщо прослiдкувати, як визначався ранг розширеної матри-
цi, то можна переконатися, що поява нуля в першому рядку i останньому
стовпцi цiєї матрицi є наслiдком умови (1.4.3):
20 + 30 = 10 + 30 + 10.
Отже, ранг системи
r =4, загальна кiлькiсть змiнних n =6,значить,
число вiльних змiнних
k = n − r =2.Виберемоx
11
та x
12
як вiльнi
змiннi. Виражаючи iншi змiннi через вiльнi, отримаємо
x
13
=20− x
11
− x
12
,
x
21
=10− x
11
,
x
22
=30− x
12
,
x
23
= −10 + x
11
+ x
12
.
(1.4.4)
Форма
F при заданiй вище матрицi вартостi перевезень дорiвнює
F =4x
11
+9x
12
+3x
13
+4x
21
+8x
22
+ x
23
= 330 − 2x
11
− x
12
.
Остаточно, додаючи вимогу невiд’ємностi усiх змiнних x
ij
,матимемо
наступну систему обмежень
20 − x
11
− x
12
≥ 0, (I)
10 − x
11
≥ 0, (II)
30 − x
12
≥ 0, (III)
−10 + x
11
+ x
12
≥ 0, (IV )
x
11
≥ 0, (V )
x
12
≥ 0, (VI)
F = 330 − 2x
11
− x
12
.
27

Рис. 1.4.6: Геометрична iнтерпретацiя задачi про перевезення.
Введемо систему координат на площинi. Осi позначимо, як x
11
i x
12
.На-
креслимо многокутник розв’язкiв i одну з лiнiй рiвня форми
F (рис. 1.4.6).
Оптимальний розв’язок дається точкою
N(10,10).Отже,x
11
=10,
x
12
=10, F
min
= 300. Iншi значення x
ij
знаходимо з рiвнянь (1.4.4):
x
13
=20− x
11
− x
12
=0,
x
21
=10− x
11
=0,
x
22
=30− x
12
=20,
x
23
= −10 + x
11
+ x
12
=10.
1.4.3. Задача про харчовий рацiон
Табл.1.4.2
Поживнi Мiнiмальна Види харчiв
речовини норма P
1
P
2
V
1
10 1 5
V
2
12 3 2
V
3
16 2 4
V
4
10 2 2
V
5
1 1 0
Вартiсть 2 3
Розв’яжемо задачу про дiєту (див. §1.1.1, стор. 8), використовуючи
наведенi в таблицi 1.4.2 значення (вони носять iлюстративний характер
i не мають реального змiсту).
28
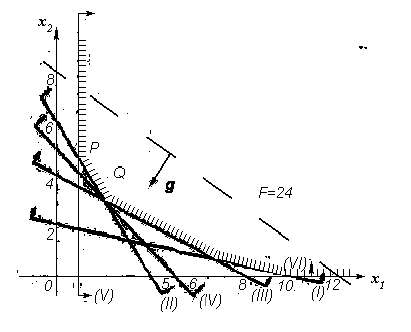
Рис. 1.4.7: Геометрична iнтерпретацiя задачi про дiєту.
Обмеження (1.1.3) i форма (1.1.2) задачi 1.1.1 при обраних вище да-
них приймають вигляд:
x
1
+5x
2
≥ 10, (I)
3x
1
+2x
2
≥ 12, (II)
2x
1
+4x
2
≥ 16, (III)
2x
1
+2x
2
≥ 10, (IV )
x
1
≥ 1, (V )
x
2
≥ 0, (VI)
F =2x
1
+3x
2
.
Накреслимо многокутник розв’язкiв i одну з лiнiй рiвня форми F
(рис. 1.4.7). Оптимальний розв’язок досягається у точцi Q(2,3);отже,
x
1
=2,x
2
=3,F =13.
Зауважимо, що у задачi, яка розглядається, “многокутник” розв’язкiв
необмежений зверху i тому на многокутнику не iснує найбiльшого зна-
чення
F . Це, очевидно, означає, що харчування можна органiзувати як
завгодно дороге.
1.4.4. Контрольнi запитання i задачi для самостiйної роботи
1. Чи може допустимий розв’язок задачi лiнiйного програмування мi-
стити вiд’ємну компоненту?
29

2. Чи може система обмежень загальної задачi лiнiйного програмува-
ння мiстити строгi нерiвностi?
3. Чим вiдрiзняється оптимальний розв’язок задачi лiнiйного програ-
мування вiд допустимого?
4. Чи може функцiя цiлi задачi лiнiйного програмування мiстити не-
лiнiйнi вирази зi змiнних?
5. Чи може задача лiнiйного програмування мати бiльше, нiж один,
оптимальних розв’язкiв?
Задачi
Сформулювати задачу лiнiйного програмування та розв’язати її гра-
фiчним методом.
1. Фiрма виготовляє два види продукцiї, використовуючи для цього
два види сировини. Витрати сировини для виготовлення одиницi
продукцiї кожного виду та її запаси подано таблицею.
Норма витрат сировини, ум. од. Запаси,
Сировина A B ум. од.
1 2 5 210
2 3 4 240
Вiддiл збуту фiрми вважає, що виробництво продукцiї B має ста-
новити не бiльш як 65 % загального обсягу реалiзацiї продукцiї
обох видiв. Цiна одиницi продукцiї
A та B дорiвнює 50 та 200 грн
вiдповiдно. Визначити оптимальний план виробництва продукцiї,
який максимiзує прибуток фiрми.
2. Банк протягом декiлькох мiсяцiв планує вкласти до $200 000 у
кредитування приватних осiб (клiєнтiв) i купiвлi автомобiлiв. Бан-
кiвськi комiсiйнi складають 14% при кредитуваннi приватних осiб
i 12% при кредитуваннi купiвлi автомобiлiв. Обидва типа креди-
тiв повертаються в кiнцi рiчного перiоду кредитування. Вiдомо, що
приблизно 3% клiєнтських i 2% автомобiльних кредитiв нiколи не
повертаються. У цьому банку об’єми кредитiв на купiвлю автомобi-
лiв звичайно бiльш нiж вдвiчi перевищують об’єми iнших кредитiв
для приватних осiб. Знайти оптимальне розмiщення коштiв по двом
описаним видам кредитування.
30
