Моклячук М.П., Ямненко Р.Є. Лекції з теорії вибору та прийняття рішень (на укр. языке)
Подождите немного. Документ загружается.


для якої перший гравець має єдину оптимальну стратегiю (
1
2
,
1
2
).Отже,
цим способом ми отримали б лише одну оптимальну стратегiю
(0,
1
2
,
1
2
)
початкової гри.
2.6. ГРАФIЧНИЙ МЕТОД РОЗВ’ЯЗУВАННЯ МАТРИЧНИХ
IГОР. IГРИ РОЗМIРНОСТI 2 ×n ТА m ×2
Нехай A =(a
ij
)
2
i=1
n
j=1
–матрицярозмiрностi2 × n.Позначимочерез
X =(x,1−x),0 ≤ x ≤ 1, змiшану стратегiю першого гравця. Якщо другий
гравець застосовує
j-у чисту стратегiю, то виграш першого гравця дорiв-
нює E
(X,j)=x×a
1j
+(1−x)×a
2j
. Залежнiсть функцiї E(X,j) вiд змiнної
x ∈ [0,1] при кожному j лiнiйна i цю залежнiсть можна зобразити на гра-
фiку у виглядi вiдрiзка прямої, що проходить через точки
(0,a
2j
),(1,a
1j
).
Якщо перший гравець вибрав значення x, то вiн може бути впевненим,
що отримає не менше, нiж
min
j
E(X,j)=α(x). Графiк цiєї функцiї при
змiнi
x ∈ [0,1] – це нижня границя всiх вiдрiзкiв прямих, якi вiдповiда-
ють стратегiям другого гравця, i є ламаною лiнiєю. Найвища точка цiєї
лiнiї має абсцису
x
∗
. У цiй точцi досягає максимуму функцiя α(x). Аб-
сциса
x
∗
точки є компонентою оптимальної стратегiї X
∗
=(x
∗
,1 − x
∗
)
першого гравця, а ордината точки дорiвнює цiнi гри.
Пояснимо цей метод на прикладах.
Приклад 2.6.1. Розглянемо гру з матрицею виграшiв
2311
75 2
.
Якщо гравець P
1
застосовує змiшану стратегiю (x,1−x),аP
2
застосовує
чисту першу стратегiю, то виграш першого гравця буде
V
1
(x)=2× x +7× (1 − x).
Якщо гравець P
2
застосовує чисту другу стратегiю, то виграш першого
гравця буде
V
2
(x)=3× x +5× (1 − x).
Якщо гравець P
2
застосовує чисту третю стратегiю, то виграш першого
гравця буде
V
3
(x)=11× x +2× (1 − x).
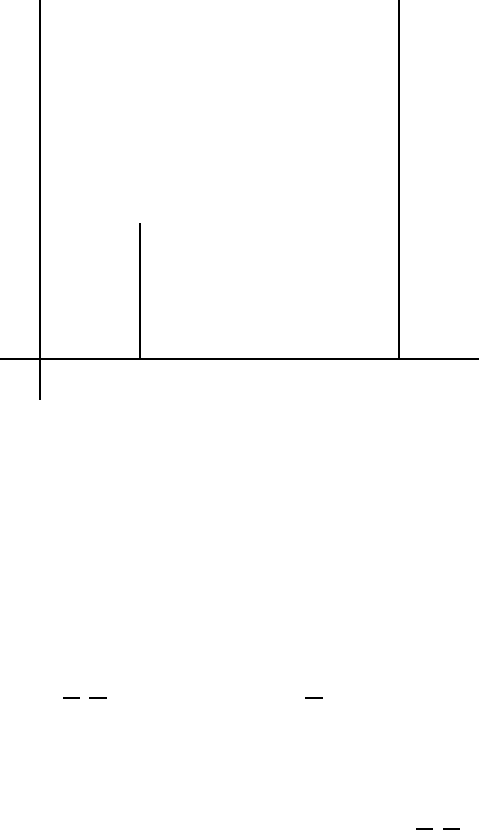
Проведемо три вiдрiзки прямих:
V
1
=7− 5x, V
2
=5− 2x, V
3
=2+9x, x ∈ [0,1].
121
6
V
1
- X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
V
1
V
2
V
3
x
∗
i
Рис. 2.6.1: Приклад 2.6.1
При кожному виборi гравцем P
1
стратегiї (x,1 − x) вiн може бути впев-
нений, що одержить принаймнi найменшу з ординат трьох прямих, що
вiдповiдають
x.Такимчином,дляP
1
вибрати оптимальне x –цезначить
вибрати таке
x, при якому найменша з трьох ординат є якнайбiльшою.
Отже, ми можемо знайти оптимальну стратегiю для
P
1
(у цiй грi є тiльки
одна оптимальна стратегiя) i цiну гри, розв’язавши рiвняння
y =5− 2x, y =2+9x.
Зробивши необхiднi обчислення, ми знаходимо, що оптимальна стратегiя
для
P
1
є (
3
11
,
8
11
) iцiнагридорiвнює
49
11
. Далi, з малюнка видно, що стра-
тегiя 1 не ввiйде в оптимальну змiшану стратегiю гравця
P
2
.Миможемо
знайти оптимальну стратегiю для
P
2
, розв’язавши гру з матрицею
311
52
.
Отже, оптимальна стратегiя для P
2
дорiвнює (0,
9
11
,
2
11
).
Зауваження. Цiна гри у наведеному вище прикладi знаходиться в такий
спосiб. Беремо максимальну ординату опуклої множини, що обмежена
зверху прямими лiнiями. Такий же метод може бути застосований для
знаходження розв’язкiв будь-якої гри з матрицею порядку
2 ×n.Длягри
зматрицеюпорядку
m × 2 графiчна побудова аналогiчна, але в цьому
122
6
V
1
- X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
V
1
V
2
V
3
x
1
i
x
2
i
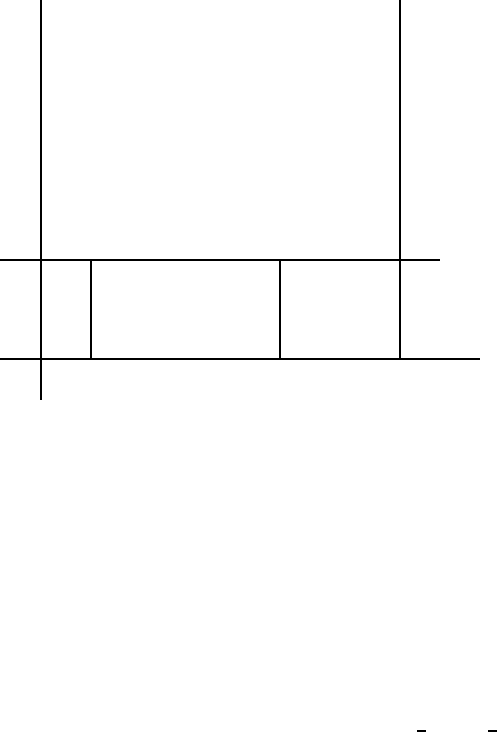
Рис. 2.6.2: Приклад 2.6.2
випадку цiна гри дорiвнює мiнiмальнiй ординатi опуклої множини, що
обмежена знизу прямими лiнiями.
Наведемо тепер приклад гри, у якiй гравець має багато оптимальних
стратегiй.
Приклад 2.6.2. Розглянемо гру з матрицею
2411
74 2
.
Аналiз рисунка показує, що оптимальною стратегiєю для першого гравця
буде будь-яка пара
(x,1−x),деx
1
≤ x ≤ x
2
, x
1
=
2
9
, x
2
=
3
5
.Оптимальною
стратегiєю другого гравця буде
(0,1,0).
2.6.1. Контрольнi запитання i задачi для самостiйної роботи
1. Як визначаються змiшанi стратегiї гравцiв?
2. Як визначаються оптимальнi змiшанi стратегiї i цiна гри?
3. Сформулюйте i доведiть основну теорему матричних iгор.
123
4. Напишiть лiнiйнi нерiвностi, яким мають задовольняти оптимальнi
змiшанi стратегiї.
5. Виведiть формули, за якими знаходиться розв’язок матричної гри
розмiрностi
2 × 2.
6. Опишiть метод розв’язування iгор розмiрностi
2 × n та m × 2.
Задачi
1. Розв’яжiть гру з матрицею A =(a
ij
)
n
i=1
m
j=1
,деa
ij
=1при i = j та
a
ij
= −1 при i = j.
2. Матриця порядку
n × n називається латинським квадратом, якщо
кожний рядок та кожний стовпчик мiстить всi цiлi числа вiд 1 до
n. Покажiть, що гра з матрицею, яка є латинським квадратом, має
цiну
(n +1)/2. Знайдiть оптимальнi стратегiї гри.
3. Розв’яжiть гру з матрицею
A =(a
ij
)
n
i=1
m
j=1
,деa
ij
=1при |i −j| =0
та |i − j| =1i a
ij
=0в iнших випадках.
4. Покажiть, що
(0,0,5/12,0,4/12,0,3/12,0,0) єоптимальноюстратегiєю
для кожного гравця у грi "three-finger Morra" (трипальцева Мор-
ра).
5. Використовуючи наведенi теореми, знайдiть формули для обчисле-
ння змiшаних стратегiй та цiни гри з матрицею розмiрностi
2 × 2.
Отриманi результати використайте, щоб розв’язати iгри з матриця-
ми:
A
1
=
34
25
,A
2
=
10
01
,A
3
=
413
234
,
A
4
=
3 −137
−1930
,A
5
=
25
43
36
54
,A
6
=
44
53
65
13
.
6. Використовуючи поняття домiнування, знайти оптимальнi стратегiї
матричних iгор:
A
1
=
340
251
650
,A
2
=
235
412
301
,A
3
=
30 2
45 1
25−1
,
124
A
4
=
0552
5022
5511
,A
5
=
00 0
0 −11
01−1
,A
6
=
24 0
08
45
.
7. Знайти оптимальнi стратегiї матричних iгор:
C
1
=
215 3
130−1
,C
2
=
223 4
431−1
,
C
3
=
5 −2370
05226
,
C
4
=
02
13
−10
21
,C
5
=
13
22
31
5 −1
,C
6
=
10
0 −1
1 −2
2 −10
,
C
7
=
−11
−28
8 −9
10 −8
,C
8
=
6 −4
5 −2
03
14
,C
9
=
3240
3424
4240
0408
,
C
10
=
000000
420211
431322
437−512
434122
433−222
.
2.7. МАТРИЧНI IГРИ ТА ЛIНIЙНЕ ПРОГРАМУВАННЯ
Нехай A =(a
ij
)
m
i=1
n
j=1
–матрицярозмiрностim ×n. До кожного еле-
менту матрицi
A можна додати сталу C так, щоб усi елементи матрицi
стали невiд’ємними. Така операцiя не змiнює оптимальнi стратегiї грав-
цiв. Вона змiнює лише цiну гри. Якщо
v – цiна гри з матрицею A,то
v + C – цiна гри з новою матрицею A
c
. За умови, що всi елементи но-
вої матрицi
A
c
стали невiд’ємними, матимемо v + C ≥ 0.Будемонадалi
вважати, що всi елементи матрицi гри невiд’ємнi i цiна гри додатна.
Серед усiх розподiлiв ймовiрностей
Y =(y
1
,...,y
n
) ∈ S
n
,щозадо-
вольняють нерiвностi
n
j=1
a
ij
y
j
≤ α, 1 ≤ i ≤ m, (2.7.1)
125

оптимальними стратегiями Y
∗
=(y
∗
1
,...,y
∗
n
) будуть вектори, що задо-
вольняють нерiвностi
n
j=1
a
ij
y
j
≤ v, 1 ≤ i ≤ m,
ацiнагриv –ценайменшеiзчиселα, якi задовольняють умови (2.7.1).
Отже, для того, щоб знайти цiну гри
v та оптимальну стратегiю Y
∗
=
(y
∗
1
,...,y
∗
n
) другого гравця, достатньо знайти найменше з чисел α,якi
задовольняють умови (2.7.1). Позначимо через
η
j
= y
∗
j
/α,1 ≤ j ≤ n.Тодi
для того, щоб знайти оптимальу стратегiю другого гравця, достатньо
розв’язати таку задачу лiнiйного програмування.
Задача 1. Знайти
max
n
j=1
η
j
=max
1
α
при обмеженнях
n
j=1
a
ij
η
j
≤ 1, 1 ≤ i ≤ m;
η
j
≥ 0, 1 ≤ j ≤ n.
Ця задача зводиться до задачi лiнiйного програмування з обмежен-
нями-рiвностями, якщо ввести додатковi змiннi.
Задача 1’. Знайти
max
n
j=1
η
j
при обмеженнях
z
i
+
n
j=1
a
ij
η
j
=1, 1 ≤ i ≤ m;
η
j
≥ 0, 1 ≤ j ≤ n, z
i
≥ 0, 1 ≤ i ≤ m.
Аналогiчно задачу про знаходження оптимальних стратегiй X
∗
=
(x
∗
1
,...,x
∗
m
) першого гравця можна звести до такої задачi лiнiйного про-
грамування.
Задача 2’. Знайти
min
m
i=1
ξ
i
,
де ξ
i
= x
i
/β, при обмеженнях
w
j
+
m
i=1
a
ij
ξ
i
=1, 1 ≤ j ≤ n;
126
ξ
i
≥ 0, 1 ≤ i ≤ m; w
j
≥ 0, 1 ≤ j ≤ n.
Задача 1’ та задача 2’ – це пара спряжених задач лiнiйного програ-
мування. Iз основної теореми матричних iгор випливає, що розв’язок
цiєї пари задач iснує. Алгоритм симплекс-методу дозволяє знайти цей
розв’язок.
Приклад 2.7.1. Розв’язати гру з матрицею
A =
01−2 −5
5075
5 −50 15
.
Додамо число 5 до всiх елементiв матрицi. Тодi всi елементи стануть
невiд’ємними. Отримаємо таку матрицю
A
c
=
563 0
1051210
10 0 5 20
.
Задача знаходження оптимальних стратегiй у грi з уазаною матрицею
зводиться до такої задачi лiнiйного програмування:
Задача. Знайти
max(0 · z
1
+0·z
2
+0· z
3
+1· η
1
+1·η
2
+1·η
3
+1· η
4
)
при умовах
1 · z
1
+0·z
2
+0· z
3
+5· η
1
+6·η
2
+3· η
3
+0· η
4
=1,
0 · z
1
+1· z
2
+0· z
3
+10·η
1
+5·η
2
+12·η
3
+10·η
4
=1,
0 · z
1
+0· z
2
+1·z
3
+10·η
1
+0·η
2
+5· η
3
+20·η
4
=1,
z
1
≥ 0,z
2
≥ 0,z
3
≥ 0,η
1
≥ 0,η
2
≥ 0,η
3
≥ 0,η
4
≥ 0.
Нехай C
1
,C
2
,...,C
7
– стовпцi матрицi, що визначає це рiвняння.
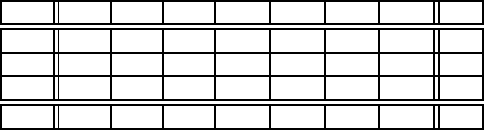
Складемо таблицю
C
1
C
2
C
3
C
4
C
5
C
6
C
7
P
C
1
1 0 0 5 6 3 0 1
C
2
0 1 0 10 5 12 10 1
C
3
0 0 1 10 0 5 20 1
0 0 0 −1 −1 −1 −1 0
В останньому рядку таблицi вказанi значення
i
a
is
q
i
− q
s
,деa
is
–
елементи матрицi,
i пробiгає iндекси базисних векторiв (у даному ви-
падку
C
1
,C
2
,C
3
), координати вектора q =(0,0,0,1,1,1,1) –цекоефiцiєн-
ти функцiї, яка дослiджується на максимум,
P =(p
1
,p
2
,p
3
)=(1,1,1).
Останнiй нуль у рядку – це значення функцiї цiлi на даному етапi
127
розв’язування. Алгоритм розв’язування розпочинається зi знаходження
базисного допустимого розв’язку. На даному етапi цей розв’язок такий:
z
1
=1,z
2
=1,z
3
=1,η
1
=0,η
2
=0,η
3
=0,η
4
=0. Наша мета полягає в
тому, щоб шляхом замiни базисного вектор-стовпця отримати базисний
допустимий розв’язок, який збiльшить значення функцiї цiлi. Цiєї мети
досягають, якщо ввести в базис вектор
C
k
та вивести з базису вектор
C
r
при умовах:
1)a
rk
> 0, 2)
i
a
ik
q
i
− q
k
< 0, 3)p
r
/a
rk
=min
i:a
ik
>0
p
i
/a
ik
.
Оскiльки кожного разу матимемо новий базис, який збiльшує значен-
ня функцiї цiлi, то за скiнченну кiлькiсть крокiв ми знайдемо оптималь-
ний розв’язок (у нижньому рядку всi елементи стануть невiд’ємними).
Для даної матрицi можна ввести в базис
C
5
(в нижньому рядку цьому
стовпчику вiдповiдає вiд’ємне число). Оскiльки
min{1/6,1/5} =1/6, то
з базису виводиться
C
1
. Щоб отримати нову таблицю, що вiдповiдає ба-
зису, зробимо перетворення старої так, щоб у стовпцi залишилась одна
одиниця, а всi iншi елементи стали нульовими. Для цього роздiлимо ря-
док, що вiдповiдає тому, який ми виводимо з базису (у даному випадку
це перший рядок), на елемент (вiн додатний), а iз iнших рядкiв вiднiме-
мо рядок, помножений на вiдповiдним чином пiдiбране число. Така сама
операцiя проводиться i з останнiм рядком. Отримаємо
i
a
is
q
i
− q
s
,де
i пробiгає iндекси базисних векторiв (у даному випадку це C
5
,C
2
,C
3
).
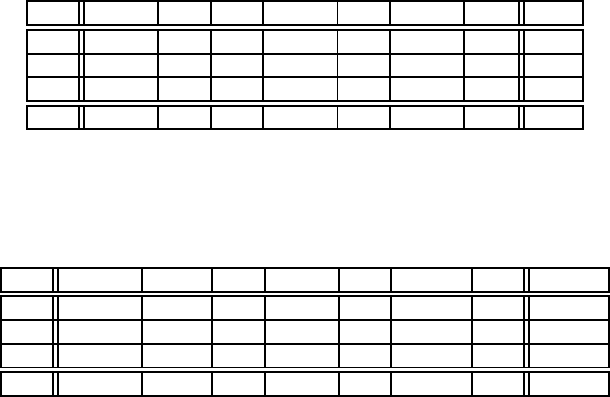
Отримаємо таку таблицю
C
1
C
2
C
3
C
4
C
5
C
6
C
7
P
C
1
1/6 0 0 5/6 1 1/2 0 1/6
C
2
−5/6 1 0 35/6 0 19/2 10 1/6
C
3
0 0 1 10 0 5 20 1
1/6 0 0 −1/6 0 − 1/2 −1 1/6
Тепер можемо ввести в базис C
7
, оскiльки вiдповiдний елемент у
нижньому рядку – вiд’ємне число. Матимемо
min{1/20,1/60} =1/60,
що вiдповiдає вектору C
2
. Отже, з базису виводиться C
2
.Новатаблиця
матиме такий вигляд.
C
1
C
2
C
3
C
4
C
5
C
6
C
7
P
C
1
1/6 0 0 5/6 1 1/2 0 1/6
C
2
−1/12 1/10 0 7/12 0 19/20 1 1/60
C
3
5/3 −2 1 −5/3 0 −14 0 2/3
1/12 1/10 0 5/12 0 9/20 0 11/60
128
Оскiльки всi елементи останнього рядка невiд’ємнi, то ми знайшли
оптимальний розв’язок задачi. З таблицi маємо, що векторам
C
3
,C
5
,C
7
вiдповiдають числа
2
3
,
1
6
,
1
60
, а значення функцiї цiлi дорiвнює
11
60
.Оскiль-
ки
1
v
=
11
60
, то цiна гри з матрицею A
c
дорiвнює
60
11
. Тодi цiна гри з матри-
цею
A дорiвнює
60
11
− 5=
5
11
. Розв’язок задачi лiнiйного програмування:
z
1
= z
2
=0,z
3
=
2
3
,η
1
=0,η
2
=
1
6
,η
3
=0,η
4
=
1
60
. Оскiльки y
∗
j
= v · η
j
,
то оптимальна стратегiя другого гравця буде такою:
Y
∗
=(0,
10
11
,0,
1
11
).
Оптимальну стратегiю першого гравця теж можна знайти з останньої
таблицi. Елементи нижнього рядка, що вiдповiдають векторам
C
1
,C
2
,C
3
такi:
1
12
,
1
10
,0.Тому
x
∗
1
= v · ξ
1
=
1
12
·
60
11
=
5
11
,x
∗
2
=
6
11
,x
∗
3
=0.
Отже, оптимальна стратегiя першого гравця буде такою: X
∗
=(
5
11
,
6
11
,0).
2.7.1. Контрольнi запитання i задачi для самостiйної роботи
1. Дайте визначення поняття домiнування стратегiй.
2. Сформулюйте i доведiть теорему про структуру розв’язку матричної
гри, в якiй є домiнування стратегiй першого гравця.
3. Сформулюйте i доведiть теорему про структуру розв’язку матричної
гри, в якiй є домiнування стратегiй другого гравця.
4. Сформулюйте i доведiть теорему про структуру розв’язку матри-
чних iгор, матрицi яких вiдрiзняються сталим множником чи до-
данком.
5. Опишiть метод зведення матричної гри до задачi лiнiйного програ-
мування.
Задачi
Користуючись симплекс-методом, знайти оптимальнi стратегiї мат-
ричних iгор:
A
1
=
2 −34
−34−5
4 −56
,A
2
=
342
160
234
,A
3
=
423
601
340
,
129
A
4
=
461
322
403
,A
5
=
01−2
−103
2 −30
,
A
6
=
3614
5242
1435
,A
7
=
01/6 −1/60
−1/601/61/3
1/6 −1/60−1/3
0 −1/31/30
,
A
8
=
00−1/5 −2/5 −3/5
001/50−1/5
1/5 −1/502/51/5
2/50−2/503/5
3/51/5 −1/5 −3/50
,
A
9
=
25−4
−12−3
3 −17
,A
10
=
135
240
034
,A
11
=
412
504
250
,
A
12
=
571
411
502
,A
13
=
13−2
−114
3 −30
,A
14
=
2715
3262
1354
,
A
15
=
1/21/6 −1/6 −1/20
001/60−1/6
1/6 −1/601/31/6
00−1/6 −1/3 −1/2
1/30−1/301/2
,
A
16
=
4 −32
−15−5
3 −57
,A
17
=
472
250
234
,A
18
=
625
404
280
,
A
19
=
5 −44
−22−5
4 −68
,A
20
=
352
360
143
,A
21
=
325
103
360
,
A
22
=
−1/401/41/3
01/4 −1/40
0 −1/31/30
1/4 −1/40−1/3
,A
23
=
2713
3262
0427
,
A
24
=
03−4
−25−3
2 −16
,A
25
=
144
130
352
,A
26
=
513
403
260
.
130
