Моклячук М.П., Ямненко Р.Є. Лекції з теорії вибору та прийняття рішень (на укр. языке)
Подождите немного. Документ загружается.

T
1
T
2
T
3
Д
1
Д
2
u
i
З
1
−1 4 2
100
M M M
0
З
2
M 6
200 −
4 5
+
M M
4
T
1
0
300
−1 1 M −3 8 M
−3
T
2
1
0
0
0 +
M 6
150
5
150 −
−2
T
3
M M 0
300 −
M 2
0 +
−5
Д
2
M M M −5 6 0
300
−7
v
j
3 2 5 8 7
Далi послiдовно покладаємо x
45
= 150, x
22
= 200, x
44
= 150, x
12
=
100
, x
42
=0, x
31
= 300, x
42
=0i викреслюємо вiдповiднi рядки i стовпцi.
Послiдовнiсть вибору клiтинок i викреслених рядкiв (стовпцiв) можна
простежити за останнiм рядком i стовпцем таблицi 1.14.2.
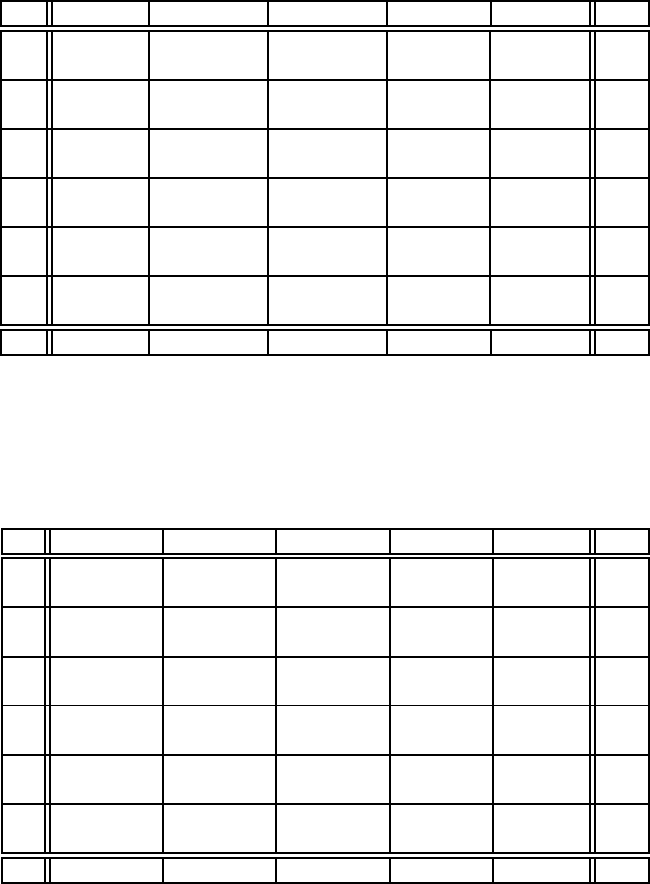
Табл.1.14.4
T
1
T
2
T
3
Д
1
Д
2
u
i
З
1
−1 4 2
100
M M M
0
З
2
M 6
50
5
150
M M
4
T
1
0
300
−1 1 M −3 8 M
−3
T
2
1
0
0
150
M 6
150
−4 5
−2
T
3
M M 0
150
M 2
150
−1
Д
2
M M M −5 6 0
300
−3
v
j
3 2 1 8 3
Застосуємо метод потенцiалiв для знаходження оптимального розв’яз-
ку. Взявши
u
1
=0, знаходимо всi iншi потенцiали. Вони занесенi в
останнiй рядок i стовпець таблицi 1.14.3. Тут же в лiвих верхнiх кутах
91

небазисних клiтинок помiщенi величини α
ij
. Оскiльки жоднiй базиснiй
клiтинцi не вiдповiдає штучна величина перевезення
M,товсiα
ij
для
таких клiтинок будуть вiд’ємними, i їх можна не розглядати.
Як бачимо, критерiй оптимальностi порушується в клiтинцi (З
2
,Т
3
).
Таким чином, вводимо у базис змiнну
x
23
за маршрутом (З
2
,Т
3
)—(З
2
,
Т
2
)—(Т
2
,Т
2
)–(Т
2
,Д
2
)–(Т
3
,Д
2
)–(Т
3
,Т
3
)–(З
2
,Т
3
). Результати об-
числень для полiпшеного плану наведенi в транспортнiй таблицi 1.14.4.
Оптимальну схему перевезення зображено на рис. 1.14.2.
З
2
Т
3
Д
2
З
1
Т
1
Д
1
Т
2
200
100
150
150
- -
>
>
Z
Z
Z
Z~
150 150
50
100
150
-
-
-
-
Рис. 1.14.2: Оптимальна схема перевезення.
1.14.1. Контрольнi запитання i задачi для самостiйної роботи
1. Чим вiдрiзняються одна вiд однiєї транспортнi задачi з правильним
i неправильним балансом?
2. Чи може транспортна задача мати 2 розв’язки? Нескiнченно багато
розв’язкiв?
3. Як покращити неоптимальний розв’язок транспортної задачi?
4. Як перевiрити на оптимальнiсть отриманий розв’язок?
5. В чому полягає метод найменших цiн отримання початкового роз-
в’язку?
6. Що таке збурена транспортна задача?
7. Чим метод Фогеля вiдрiзняється вiд методу найменших цiн?
92
8. Яким чином транспортну задачу iз промiжними пунктами переве-
зення можна перетворити на звичайну?
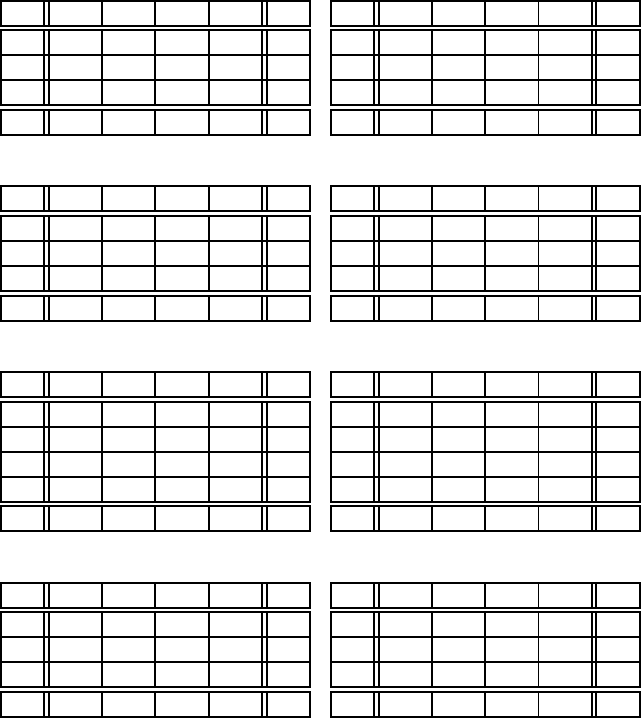
Задачi
Розв’язати транспортнi задачi, заданi в таблицях:
Таблиця 1 Таблиця 2
B
1
B
2
B
3
B
4
a
i
A
1
1 8 2 3 30
A
2
4 7 5 1 50
A
3
5 3 4 4 20
b
j
15 15 40 30
B
1
B
2
B
3
B
4
a
i
A
1
2 4 5 1 60
A
2
2 3 9 4 70
A
3
3 4 22 5 20
b
j
40 30 30 50
Таблиця 3 Таблиця 4
B
1
B
2
B
3
B
4
a
i
A
1
2 6 3 4 40
A
2
1 5 6 9 30
A
3
3 4 1 6 35
b
j
20 34 16 25
B
1
B
2
B
3
B
4
a
i
A
1
4 5 6 10 95
A
2
10 3 3 15 90
A
3
4 10 1 16 75
b
j
90 70 60 90
Таблиця 5 Таблиця 6
B
1
B
2
B
3
B
4
a
i
A
1
1 3 3 4 50
A
2
5 2 7 5 20
A
3
6 4 8 2 30
A
4
7 1 5 7 20
b
j
40 30 35 15
B
1
B
2
B
3
B
4
a
i
A
1
2 4 1 3 30
A
2
5 6 5 4 20
A
3
3 7 9 5 40
A
4
1 2 2 7 50
b
j
35 20 55 30
Таблиця 7 Таблиця 8
B
1
B
2
B
3
B
4
a
i
A
1
2 4 5 1 60
A
2
2 3 9 4 70
A
3
3 4 2 5 20
b
j
40 30 30 50
B
1
B
2
B
3
B
4
a
i
A
1
1 2 6 4 40
A
2
3 1 3 2 30
A
3
5 7 5 1 20
b
j
30 25 18 20
93
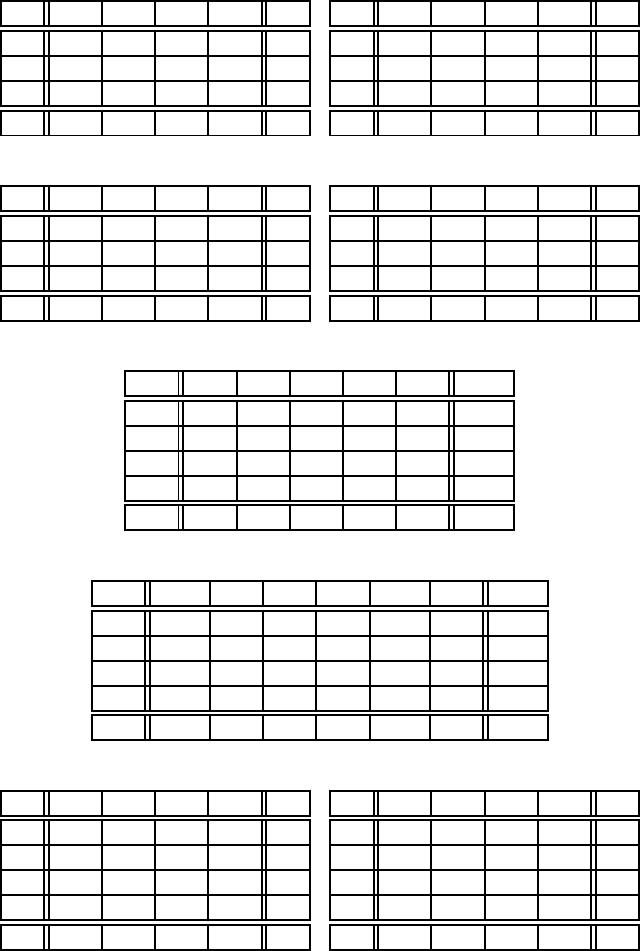
Таблиця 9 Таблиця 10
B
1
B
2
B
3
B
4
a
i
A
1
2 4 3 2 60
A
2
3 1 2 3 65
A
3
5 4 1 5 70
b
j
40 60 70 25
B
1
B
2
B
3
B
4
a
i
A
1
10 5 7 4 40
A
2
7 4 9 10 25
A
3
6 14 8 7 35
b
j
15 40 30 15
Таблиця 11 Таблиця 12
B
1
B
2
B
3
B
4
a
i
A
1
3 2 4 1 50
A
2
2 3 1 5 40
A
3
3 2 7 4 20
b
j
30 25 35 20
B
1
B
2
B
3
B
4
a
i
A
1
18 2 9 7 38
A
2
30 4 1 55 55
A
3
6 4 8 3 40
b
j
20 30 30 16
Таблиця 13
B
1
B
2
B
3
B
4
B
5
a
i
A
1
8 12 4 9 10 60
A
2
7 5 15 3 6 40
A
3
9 4 6 12 7 100
A
4
5 3 2 6 4 50
b
j
30 80 65 35 40
Таблиця 14
B
1
B
2
B
3
B
4
B
5
B
6
a
i
A
1
2 3 6 8 2 10 130
A
2
8 1 2 3 5 6 90
A
3
7 4 4 1 4 8 100
A
4
2 8 5 1 3 6 140
b
j
110 50 30 80 100 90
Таблиця 15 Таблиця 16
B
1
B
2
B
3
B
4
a
i
A
1
1 2 9 7 60
A
2
3 40 15 5 55
A
3
6 4 8 3 40
A
4
24 3 3 1 35
b
j
70 5 45 70
B
1
B
2
B
3
B
4
a
i
A
1
2 3 9 7 20
A
2
3 4 6 1 16
A
3
5 1 2 2 14
A
4
4 5 8 1 11
b
j
16 18 12 15
94
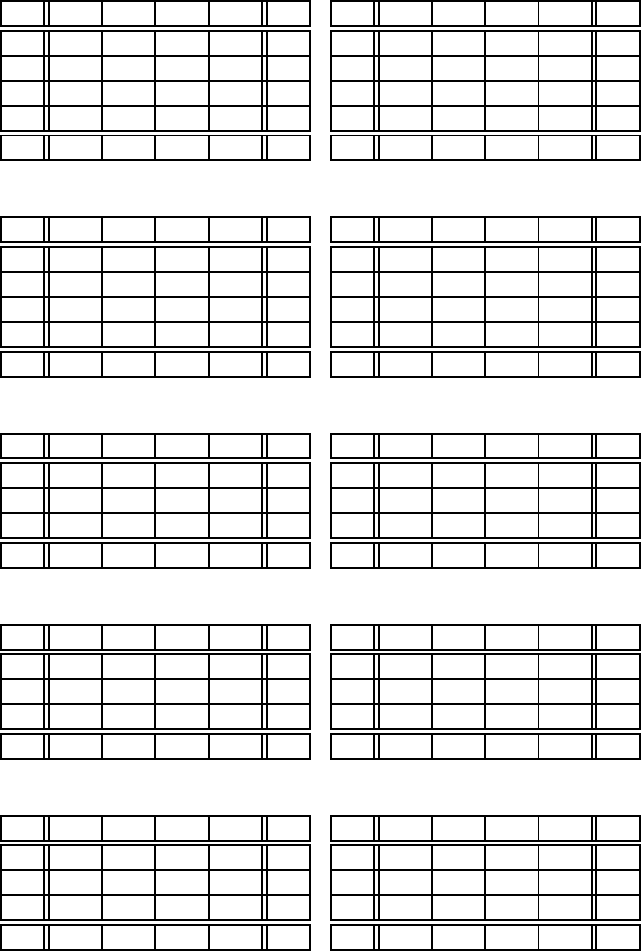
Таблиця 17 Таблиця 18
B
1
B
2
B
3
B
4
a
i
A
1
3 7 1 5 30
A
2
7 5 8 6 5
A
3
6 4 8 3 45
A
4
3 1 7 4 70
b
j
10 35 40 35
B
1
B
2
B
3
B
4
a
i
A
1
4 5 5 7 10
A
2
8 7 5 4 20
A
3
9 6 4 5 50
A
4
3 2 9 3 30
b
j
40 30 20 40
Таблиця 19 Таблиця 20
B
1
B
2
B
3
B
4
a
i
A
1
1 3 3 8 20
A
2
8 6 2 6 20
A
3
7 7 3 8 40
A
4
5 2 4 5 45
b
j
25 30 40 15
B
1
B
2
B
3
B
4
a
i
A
1
3 2 1 7 10
A
2
8 6 2 6 20
A
3
5 2 4 5 45
A
4
4 7 7 3 35
b
j
25 15 40 30
Таблиця 21 Таблиця 22
B
1
B
2
B
3
B
4
a
i
A
1
2 5 3 4 45
A
2
6 1 2 5 35
A
3
3 4 3 8 70
b
j
20 60 55 45
B
1
B
2
B
3
B
4
a
i
A
1
1 7 2 5 40
A
2
3 8 4 1 30
A
3
6 3 5 3 50
b
j
20 18 44 75
Таблиця 23 Таблиця 24
B
1
B
2
B
3
B
4
a
i
A
1
2 7 3 6 30
A
2
9 4 5 7 70
A
3
5 7 6 2 50
b
j
10 40 20 60
B
1
B
2
B
3
B
4
a
i
A
1
1 9 7 2 30
A
2
3 1 2 5 40
A
3
2 3 1 3 60
b
j
35 20 25 70
Таблиця 25 Таблиця 26
B
1
B
2
B
3
B
4
a
i
A
1
8 4 1 7 70
A
2
2 7 3 6 30
A
3
5 8 6 2 50
b
j
20 30 30 50
B
1
B
2
B
3
B
4
a
i
A
1
2 4 0 3 60
A
2
3 1 2 5 40
A
3
1 9 7 2 30
b
j
40 25 35 60
95

Таблиця 27 Таблиця 28
B
1
B
2
B
3
B
4
a
i
A
1
3 5 3 6 30
A
2
9 4 5 7 20
A
3
3 2 1 5 40
A
4
5 2 7 6 50
b
j
40 20 20 50
B
1
B
2
B
3
B
4
a
i
A
1
7 2 9 1 30
A
2
2 1 3 5 40
A
3
6 8 3 4 70
A
4
2 3 1 3 60
b
j
35 80 25 70
Таблиця 29 Таблиця 30
B
1
B
2
B
3
B
4
a
i
A
1
2 6 3 4 80
A
2
1 5 6 9 60
A
3
3 4 1 6 70
b
j
40 65 35 50
B
1
B
2
B
3
B
4
a
i
A
1
4 5 6 10 75
A
2
10 3 3 15 70
A
3
4 10 1 16 55
b
j
75 55 45 75
96

Роздiл II
Елементи теорiї iгор
2.1. МАТРИЧНI IГРИ
Гра двох гравцiв з нульовою сумою (антагонiстична гра), у якiй пер-
ший гравець має
m стратегiй (варiантiв дiї), а другий гравець має n
стратегiй (варiантiв дiї), задається матрицею A =(a
ij
)
m
i=1
n
j=1
розмiрно-
стi
m × n.РядкиматрицiA вiдповiдають стратегiям першого гравця, а
стовпчики вiдповiдають стратегiям другого гравця. Елемент
a
ij
матрицi
A – це виграш першого гравця у другого за умови, що перший гравець
застосовує
i-ту стратегiю, а другий гравець застосовує j-ту стратегiю.
При цьому виграш другого гравця дорiвнює
−a
ij
.
Наведемо приклад матричної гри. Гравець
P
1
вибирає одне число з
множини чисел
{1,2,3},агравецьP
2
вибирає число з множини чисел
{1,2,3,4}, не будучи iнформованим про те, який вибiр зробив P
1
.Пiсля
того,яквиборибулизробленi,гравець
P
2
платить гравцю P
1
суму, яка
визначається таблицею:
1234
1 2 1 10 11
2 0 −1 12
3 −3 −5 −1 1
Аналiз таблицi показує, що якщо, наприклад, гравець P
1
вибирає 1,
агравець
P
2
вибирає 3, то гравець P
2
платить гравцю P
1
десять гривень
(чи десять доларiв, чи десять будь-яких iнших грошових одиниць). Якщо
P
1
вибирає 3, а P
2
вибирає 2, то гравець P
2
платить гравцю P
1
мiнус
п’ять гривень, тобто гравець
P
1
платить гравцю P
2
п’ять гривень. Ми
будемо описувати надалi таку гру, вказуючи просто її матрицю виграшiв
гравця
P
1
угравцяP
2
:
2 1 10 11
0 −11 2
−3 −5 −11
Iнший приклад прямокутної гри – це так звана гра “two-finger Morra”
(двопальцева Морра), у яку грали в Iталiї з античних часiв. У цю гру
грають два гравцi: кожний з них показує один чи два пальцi i одноча-
сно називає число пальцiв, що, на його думку, покаже його супротивник.
Якщо один iз гравцiв угадує правильно, то вiн виграє суму, яка дорiвнює
97

сумi пальцiв, показаних ним i його супротивником, В iнших випадках
– нiчия. Якщо символ
1,2 означатиме, що гравець показує один па-
лець i припускає, що його супротивник показує два пальцi, то матриця
виграшiв для цiєї гри буде мати вигляд
1,11,22,12,2
1,1 02−3 0
1,2 − 2 003
2,1 300−4
2,2 0 −3 40
Найважливiшим питанням у випадку як матричної, так i взагалi будь-
якої гри, є питання про те, чи iснує оптимальний спосiб гри, тобто чи
можна довести, що даний спосiб гри є найбiльш рацiональним. Вияв-
ляється, що у першому прикладi на це питання дуже легко вiдповiсти.
Дiйсно, зауважимо, що кожен елемент першого рядка бiльший вiдпо-
вiдного елемента другого рядка i також бiльший вiдповiдного елемента
третього рядка. Отже, незалежно вiд того, яке число вибирає гравець
P
2
для P
1
краще вибрати першу стратегiю, нiж другу чи третю. Отже,
оптимальний спосiб гри для гравця
P
1
–цевибрати1.Точнотаксамо
кожен елемент другого стовпця менше вiдповiдного елемента кожного
з iнших стовпцiв. Тому, оскiльки
P
2
хоче грати таким чином, щоб пла-
та була якомога меншою, то оптимальний спосiб гри для
P
2
–вибрати
сратегiю 2.
Цей висновок оснований на специфiчнiй властивостi матрицi вигра-
шiв,тобтонатому,щокоженелементданогорядка(чистовпця)бiльше
вiдповiдного елемента iншого рядка (чи стовпця). Для того, щоб дати
аналiз матричних iгор, який можна було б застосувати для бiльш широ-
кого класу iгор, ми повиннi будемо ввести деякi новi поняття.
2.2. МАТРИЧНI IГРИ З СIДЛОВИМИ ТОЧКАМИ
Розглянемо матричну гру з матрицею розмiрностi m × n
A =
a
11
a
12
... a
1n
a
21
a
22
... a
2n
... ... ... ...
a
m1
a
m2
... a
mn
.
Якщо гравець P
1
у деякiй партiї цiєї гри вибирає перший варiант дiї,
тобто перший рядок, то йому буде сплачений принаймнi мiнiмальний
елемент цього рядка, тобто щонайменше
min
j
a
1j
.
98
Якщо гравець P
1
вибирає i-й рядок, то йому обов’язково буде сплачено
щонайменше величину
min
j
a
ij
.
Але оскiльки вiн може рядки вибирати, то може, зокрема, вибрати так,
щоб зробити величину виграшу
min
j
a
ij
найбiльшою. Отже, для P
1
євибiр,щогарантуєйому,щовiнодержить
принаймнi
max
i
min
j
a
ij
.
Аналогiчно, виграшi гравця P
2
–цеелементиматрицiA,взятiзi
знаком мiнус. Ми бачимо, що у гравця
P
2
євибiр,якийгарантуєйому,
що вiн одержить щонайменше
max
j
min
i
(−a
ij
) .
Нагадаємо тепер елементарнi властивостi максимумiв i мiнiмумiв:
якщо
f(x) – будь-яка дiйсна функцiя, найбiльше i найменше значення
якої iснують, тo
max
x
[−f(x)] = −min
x
[f(x)] ; min
x
[−f(x)] = −max
x
[f(x)] .
Оскiльки в даному випадку i, j мають скiнченнi областi змiни i всi
максимуми i мiнiмуми iснують, то справедливе таке спiввiдношення
max
j
min
i
(−a
ij
)=max
j
!
−max
i
(a
ij
)
"
= −min
j
max
i
(a
ij
) .
Тому P
2
може грати так, щоб одержати принаймнi
−min
j
max
i
(a
ij
) ,
i, отже, так, що P
1
одержить якнайбiльше
min
j
max
i
(a
ij
) .
Величина α = α
i
0
=max
i
α
i
=max
i
min
j
a
ij
називається нижньою
цiною гри (максимiном гри). Вiдповiдно стратегiя
i
0
називається ма-
ксимiнною. Якщо перший гравець вибирає свою максимiнну стратегiю,
то при будь-якому виборi другого гравця йому забезпечений виграш не
менше, нiж
α.
Величина
β = β
j
0
=min
j
β
j
=min
j
max
i
a
ij
називається верхньою
цiною гри (мiнiмаксом гри). Вiдповiдно стратегiя
j
0
називається мiнiма-
ксною. Якщо другий гравець вибирає свою мiнiмаксу стратегiю, то при
будь-якому виборi першого гравця вiн програє не бiльше, нiж
β.
Отже,
P
1
може гарантувати собi, що вiн одержить щонайменше
max
i
min
j
a
ij
,
99
а P
2
можеперешкодитийомуодержатибiльше,нiж
min
j
max
i
(a
ij
) .
Якщо виявляється, що
max
i
min
j
a
ij
=min
j
max
i
a
ij
= v, (2.2.1)
тo
P
1
повинен розумiти, що вiн може одержати v, а його супротивник
може перешкодити йому одержати бiльше, нiж
v.Такимчином,якщо
тiльки
P
1
не має серйозних причин думати, що P
2
буде чинити нерозва-
жливо,
P
1
може грати так, щоб одержати v.Аналогiчно,P
2
може грати
так, щоб одержати
−v.
Якби рiвнiсть (2.2.1) була справедлива для всiх матриць, то пошу-
ки оптимального способу гри в матричну гру на цьому б закiнчилися.
Але, на жаль, становище не таке просте. Дiйсно, легко вказати прикла-
ди матриць, для яких (2.2.1) не виконується. Розглянемо, наприклад,
матрицю
+1 −1
−1+1
Для такої матрицi
max
i
min
j
a
ij
=max
#
min
j
a
1j
, min
j
a
2j
$
=max[− 1, − 1] = −1,
min
j
max
i
a
ij
=min
%
max
i
a
ij
, max
i
a
ij
&
=max[+1, +1]=+1.
max
i
min
j
a
ij
=min
j
max
i
a
ij
.
Оскiльки рiвнiсть (2.2.1) надзвичайно важлива в теорiї iгр, ми, при-
родно, повиннi знайти необхiднi i достатнi умови її виконання. Оскiльки
цi умови нам знадобляться надалi в бiльш загальному виглядi, ми одер-
жимо їх для дiйсних функцiй, вивiвши для матриць лише як наслiдок.
Ми доведемо насамперед, що максимальна величина мiнiмумiв нiколи
не буває бiльшою мiнiмальної величини максимумiв.
Теорема 2.2.1. Нехай є дiйсна функцiя двох змiнних
f(x,y), x ∈ A,
y ∈ B,таiснують
max
x∈A
min
y∈B
f(x,y), min
y∈B
max
x∈A
f(x,y).
Тодi
max
x∈A
min
y∈B
f(x,y) ≤ min
y∈B
max
x∈A
f(x,y).
Доведення. Для будь-яких фiксованих x та y за визначенням мiнiмуму
min
y∈B
f(x,y) ≤ f(x,y),
100
