Моклячук М.П., Ямненко Р.Є. Лекції з теорії вибору та прийняття рішень (на укр. языке)
Подождите немного. Документ загружается.

Наслiдок. Будь-яка сукупнiсть з (m + n) клiтин матрицi утворює
цикл.
Доведення. Справдi, в сукупностi вiдповiдних векторiв умов задачi не
бiльше як
m + n − 1 лiнiйно незалежних, так що в цiлому згаданi m + n
вектори лiнiйно залежнi мiж собою. Як видно з другої частини теоре-
ми 1.12.2, вiдповiднi клiтини завжди утворюють цикл.
Звiдси випливає важливий висновок: сукупнiсть усiх базисних та
однiєї вiльної клiтини таблицi утворює цикл.
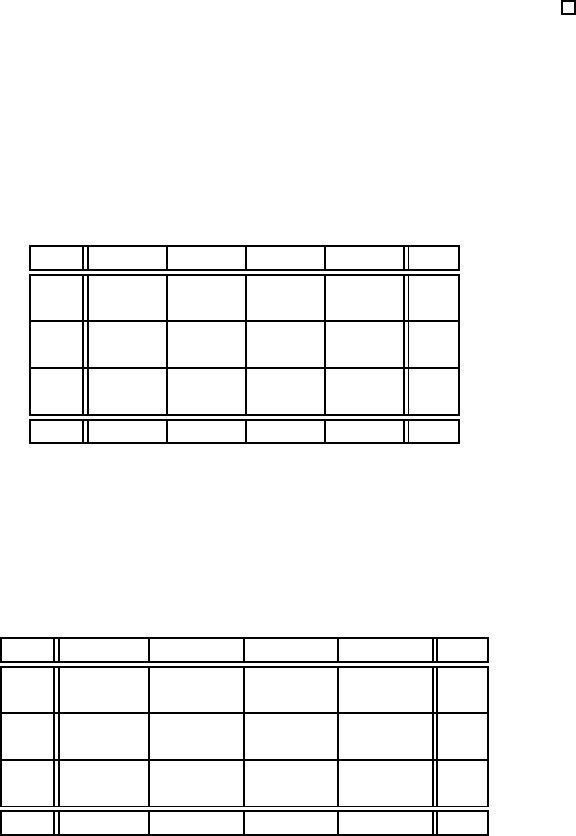
Розв’яжемо транспортну задачу, що задається транспортною табли-
цею 1.12.2. Побудуємо початковий план методом пiвнiчно-захiдного ку-
та. Результат запишемо до таблицi 1.12.3, видiливши отриманi значення
грубим шрифтом.
Табл.1.12.2
B
1
B
2
B
3
B
4
a
i
A
1
1 3 7 1
10
A
2
2 4 2 3
15
A
3
6 5 4 1
7
b
j
3 5 10 14
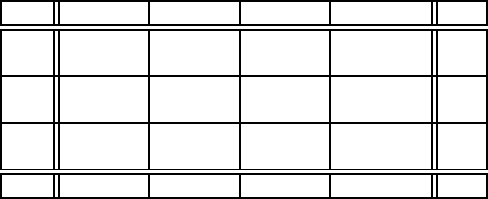
Оскiльки при побудовi початкового плану методом пiвнiчно-захiдного
кута вартiсть перевезень до уваги не бралася, то побудований таким ме-
тодом план може не бути оптимальним. Проте вiн є базисним. Щоб зна-
йти кращий план перевезень, потрiбно перейти до нової вершини областi
допустимих розв’язкiв.
Табл.1.12.3
B
1
B
2
B
3
B
4
a
i
A
1
1
3
− 3
5
+7
2
1
10
A
2
2 4 − 2
8
+3
7
15
A
3
6 +5 4 − 1
7
7
b
j
3 5 10 14
81
Перехiд вiд однiєї вершини до iншої за допомогою процедури симп-
лекс-методу вiдбувається шляхом замiни базисної та вiльних змiнних.
Для цього виберемо вiльну клiтинку, наприклад (3,2). У тому випадку,
коли план перевезень невироджений (
m + m − 1 ненульових клiтинок),
можна однозначно вибрати замкнутий маршрут (називається циклом),
який складається з вертикальних i горизонтальних вiдрiзкiв так, щоб
одна з вершин знаходилась у вибранiй клiтинцi, а iншi вершини знахо-
дились у зайнятих клiтинках. У даному випадку — це такий маршрут:
(3,2)
→ (1,2) → (1,3) → (2,3) → (2,4) → (3,4) → (3,2). Збiльшимо
кiлькiсть перевезень у вибранiй клiтинцi на число
θ. Щоб план пере-
везень залишився допустимим, потрiбно збiльшити кiлькiсть перевезень
на
θ у клiтинках, якi позначенi знаком (+) i зменшити кiлькiсть пере-
везень на
θ уклiтинках,якiпозначенiзнаком(−). Для того, щоб план
перевезень залишився базисним, потрiбно вибрану клiтинку завантажи-
ти максимально. Величина
θ при такiй замiнi визначається мiнiмальним
значенням перевезень, що стоять у клiтинках зi знаком (
−). Для даної
задачi
θ =min{5,8,7} =5.
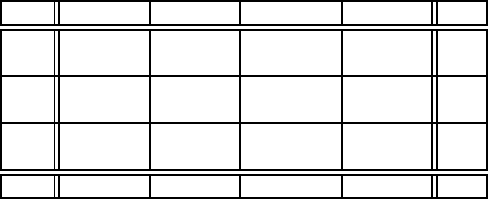
Перейшовши до нового базисного розв’язку, отримаємо транспортну та-
блицю 1.12.4.
Таким чином, в транспортнiй задачi можна легко перейти вiд одного
базисного розв’язку до iншого базисного розв’язку. Як же вибрати розв’я-
зок, що зменшує вартiсть перевезень? Для того щоб вибрати правильну
замiну, порiвняємо вартiсть перевезень. Вартiсть перевезень початкового
плану, який ми знайшли за методом пiвнiчно-захiдного кута, дорiвнює
f
0
=
3
i=1
4
j=1
c
ij
x
0
ij
,
де величини c
ij
та x
0
ij
вказанi в таблицi. При переходi до нового бази-
сного розв’язку значення вартостi перевезень змiниться на величину
f
1
− f
0
=(c
32
− c
12
+ c
13
− c
23
+ c
24
− c
34
)θ =(c
32
− z
32
)θ.
Табл.1.12.4
B
1
B
2
B
3
B
4
a
i
A
1
1
3
3 7
7
1
10
A
2
2 4 2
3
3
12
15
A
3
6 5
5
4 1
2
7
b
j
3 5 10 14
82
Отже, клiтинку (3,2) доцiльно ввести в число базисних, якщо c
32
−
z
32
< 0. У даному випадку ця умова не виконується. Вказаним вимогам
задовольняє клiтинка (1,4), для якої
c
14
− z
14
=1− 3+2− 7 < 0.
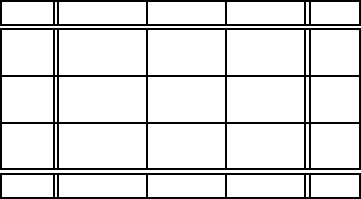
Пiсля всiх замiн отримаємо оптимальний план перевезень, що задає-
ться транспортною таблицею 1.12.5.
Отже, для того, щоб вибрати вiльну змiнну, яку доцiльно включи-
ти до складу базисного розв’язку, потрiбно для кожної вiльної змiнної
обчислити величину
c
ij
− z
ij
i вибрати ту iз змiнних, для якої
c
kl
− z
kl
=min
(i,j): c
ij
−z
ij
<0
(c
ij
− z
ij
).
Якщо для деякого плану перевезень циклiв, що задовольняють умову
c
ij
−z
ij
< 0, в таблицi не залишилось, то покращення плану неможливе,
тобто цей план перевезень оптимальний. Задача розв’язана.
Табл.1.12.5
B
1
B
2
B
3
B
4
a
i
A
1
1 3
3
7 1
7
10
A
2
2
3
4
2
2
10
3
15
A
3
6 5 4 1
7
7
b
j
3 5 10 14
Оскiльки число вершин обмежене, то за скiнченну кiлькiсть крокiв ми
одержимо розв’язок транспортної задачi лiнiйного програмування в то-
му випадку, якщо на кожнiй iтерацiї немає виродження, тобто значення
функцiї цiлi зменшується. Якщо ж на деякiй iтерацiї базисний розв’я-
зок вирождений, то при переходi до нового розв’язку значення функцiї
цiлi не зменшується i виникає небезпека зациклення, тобто повернення
до вже переглянутих вершин. Як i у випадку загальної задачi лiнiйно-
го програмування, у транспортнiй задачi зациклення можна уникнути
методом збурень. У даному випадку можна запропонувати спецiальний
метод збурень: додаємо до всiх
a
i
,i =1,2,...,m мале число ε>0,збiль-
шуючи тим самим сумарний запас вантажу на
mε > 0.Томунеобхiдно
заявку одного iз споживачiв (наприклад,
B
n
)збiльшитинаmε > 0 для
збереження (12.1) i розв’язати збурену транспортну задачу. Поклавши
ε =0, отримаємо розв’язок початкової задачi.
83
1.13. ДВОЇСТИЙ КРИТЕРIЙ ОПТИМАЛЬНОСТI ДЛЯ
ТРАНСПОРТНОЇ ЗАДАЧI
Щоб описати двоїсту до транспортної задачi (1.12.1) – (1.12.5), по-
значимо двоїстi змiннi, що вiдповiдають обмеженням-рiвностям (1.12.2)
через
−u
i
,i =1,...,m, а змiннi, що вiдповiдають обмеженням-рiвностям
(1.12.3), позначимо через
v
j
,j =1,...,n. У транспортнiй задачi величи-
ни
u
i
,v
j
називаються потенцiалами пунктiв вiдправлення A
i
та пунктiв
призначення
B
j
вiдповiдно.
Двоїста до транспортної задачi (1.12.1) – (1.12.5) задача буде та-
кою: знайти потенцiали
u
i
,i =1,...,m, v
j
,j =1,...,n, що задовольняють
обмеження
v
j
− u
i
≤ c
ij
,i=1,...,m; j =1,...,n,
та максимiзують функцiю цiлi
n
j=1
v
j
b
j
−
m
i=1
u
i
a
i
.
Тут a
i
– запас вантажу в пунктi вiдправлення A
i
,аb
j
–вимогавантажу
в пунктi призначення
B
j
.
Двоїстий критерiй оптимальностi для транспортної задачi формулює-
ться так.
Теорема 1.13.1. (Критерiй оптимальностi.) Для того, щоб допусти-
мий план перевезень
x
ij
,i =1,...,m,j =1,...,n, у транспортнiй зада-
чi (1.12.1) — (1.12.5) був оптимальним, необхiдно i достатньо, щоб
знайшлися потенцiали
u
i
,i =1,...,m, v
j
,j =1,...,n,такi,що
v
j
− u
i
= c
ij
, якщо x
ij
> 0, (1.13.1)
v
j
− u
i
≤ c
ij
, якщо x
ij
=0. (1.13.2)
На пiдставi сформульованого критерiю оптимальностi (1.13.1)–(1.13.2)
побудований метод потенцiалiв розв’язування транспортної задачi лi-
нiйного програмування. За цим методом як перше наближення до опти-
мального плану береться будь-який базисний план (побудований, напри-
клад, за методом пiвнiчно-захiдного кута). Для цього вибраного пла-
ну, у якому
m + n − 1 базисних клiток, можна визначити потенцiали
u
i
,i =1,...,m, v
j
,j =1,..., n так, щоб для кожної базисної клiтинки
виконувалася умова
v
j
− u
i
= c
ij
. (1.13.3)
Оскiльки система (1.13.2) мiстить
m + n −1 рiвнянь i m + n невiдомих,
то одну з невiдомих можна задати довiльно (наприклад, прирiвняти до
84
нуля).Пiслятогозm+ n−1 рiвнянь (1.13.3) визначаються iншi потенцi-
али i для кожної з вiльних клiток обчислюються величини
α
ij
= v
j
−u
i
.
Якщо виявилося, що
α
ij
≤ c
ij
, то план оптимальний. Якщо ж принаймнi
для однiєї вiльної клiтинки
α
ij
>c
ij
, то план не оптимальний i може
бути полiпшений шляхом описаного вище переносу по циклу, що вiдпо-
вiдає данiй вiльний клiтинцi. Процес полiпшення плану продовжується
доти, поки не будуть виконанi умови (1.13.1) – (1.13.2).
Розв’яжемо цим методом конкретну транспортну задачу, що задана
таблицею
Табл.1.13.1
B
1
B
2
B
3
a
i
A
1
10 5 4
40
A
2
6 4 5
23
A
3
7 3 6
20
b
j
20 20 43
Початковий базисний розв’язок, побудований за методом пiвнiчно-захiд-
ного кута, вироджений. Тому потрiбно розглянути “збурену” задачу. У
таблицi 1.13.2 наведена “збурена” задача i початковий базисний розв’я-
зок, що є невиродженим.
Визначимо потенцiали
u
1
,u
2
,u
3
,v
1
,v
2
,v
3
так, щоб для кожної базисної
клiтинки виконувалася умова
v
j
− u
i
= c
ij
.Уданомувипадкуматимемо
рiвняння
v
1
− u
1
=10,v
2
− u
1
=5,v
3
− u
1
=4,v
3
− u
2
=5,v
3
− u
3
=6.
Взявши u
1
=0, знаходимо всi iншi потенцiали. Вони занесенi в остан-
нiй рядок i стовпець розширеної транспортної таблицi. Тут же в лiвих
верхнiх кутах вiльних клiтинок помiщенi величини
α
ij
. Як бачимо, кри-
терiй оптимальностi порушується в усiх вiльних клiтках. У такiй ситуа-
цiї базисною може бути вибрана будь-яка вiльна клiтинка, чи клiтинка,
де досягається максимум
max(α
ij
− c
ij
).
Табл.1.13.2
85
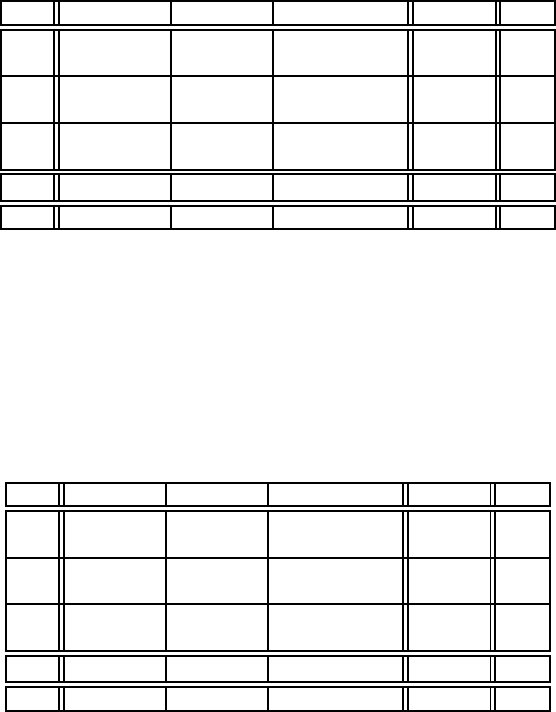
B
1
B
2
B
3
˜a
i
u
i
A
1
10
20
5
20
4
ε
40 + ε 0
A
2
11 6 6 4 5
23 + ε
23 + ε −1
A
3
12 7 7 3 6
20 + ε
20 + ε −2
˜
b
j
20 20 43 + 3ε
v
j
10 5 4
Iз цих мiркувань у базис вводимо змiнну x
21
за маршрутом (2,1)
— (1,1) — (1,3) – (2,3) – (2,1). Результати обчислень для полiпшеного
плану наведенi в наступнiй таблицi
Табл.1.13.3
B
1
B
2
B
3
˜a
i
u
i
A
1
5 10 5
20
4
20 + ε
40 + ε −4
A
2
6
20
6 4 5
3 + ε
23 + ε −5
A
3
7 7 7 3 6
20 + ε
20 + ε −6
˜
b
j
20 20 43 + 3ε
v
j
1 1 0
Тут при обчисленнi потенцiалiв ми брали v
3
=0. Можемо переконатися,
що у таблицi усе ще є вiльнi клiтки, для яких
α
ij
>c
ij
.Наприклад,клi-
тинка (2,2) та клiтинка(3,2). Перенос 20 одиниць вантажу по маршруту
(1,2) – (1,3) – (3,3) – (3,2) — (1,2) приводить до нового плану, який
представлений разом iз
v
j
,u
i
,α
ij
внаступнiйтаблицi
Табл.1.13.4
86

B
1
B
2
B
3
˜a
i
u
i
A
1
5 10 1 5 4
40 + ε
40 + ε −4
A
2
6
20
2 4 5
3 + ε
23 + ε −5
A
3
7 7 3
20
6
ε
20 + ε −6
˜
b
j
20 20 43 + 3ε
v
j
1 −3 0
Отриманий план є оптимальним планом “збуреної” задачi. Поклавши
ε =0, отримаємо оптимальний план вихiдної задачi:
x
11
=0,x
12
=0,x
13
=40,x
21
=20,x
22
=0,x
23
=3,
x
31
=0,x
32
=20,x
33
=0.
Мiнiмальна вартiсть перевезень, що вiдповiдає цьому оптимальному пла-
ну, дорiвнює 355.
Зауважимо, що загальний запас вантажу в пунктах вiдправлення мо-
же не дорiвнювати сумарнiй вимозi пунктiв споживання, тобто можливi
два випадки:
m
i=1
a
i
<
n
j=1
b
j
,
m
i=1
a
i
>
n
j=1
b
j
.
У першому випадку всiх заявок задовольнити не можна, але план пере-
везень, що вiдповiдає мiнiмуму транспортних витрат, побудувати можна.
Для цього вводиться фiктивний пункт вiдправлення
A
m+1
ззапасом
a
m+1
=
n
j=1
b
j
−
m
i=1
a
i
,
дляякоговсiвартостiперевезеньрiвнiнулю.Якщоx
m+1,j
> 0 вопти-
мальному планi такої розширеної задачi, то це означає, що вiдповiдна
величина попиту пункту
B
j
залишилася незадоволеною.
У другому випадку розширення транспортної задачi здiйснюється
шляхом введення фiктивного пункту споживання
B
n+1
, якому припи-
сується вимога
b
n+1
=
m
i=1
a
i
−
n
j=1
b
j
i вартiсть перевезення в який дорiвнює нулю. При цьому x
i,n+1
> 0 в
оптимальному планi такої розширеної задачi означає, що у пунктi вiд-
правлення
A
i
залишилися невiдправленими x
i,n+1
одиниць вантажу.
87
1.14. ТРАНСПОРТНА ЗАДАЧА З ПРОМIЖНИМИ
ПУНКТАМИ ПЕРЕВЕЗЕННЯ
Транспортна модель iз промiжними пунктами вiдповiдає реальнiй си-
туацiї, коли мiж вихiдними i кiнцевими пунктами перевезення є промi-
жнi пункти для тимчасового зберiгання вантажiв (транзитнi пункти).
Ця модель є бiльш загальною, нiж звичайна транспортна, де перевезення
вiдбувається безпосередньо мiж пунктами вiдправлення i призначення.
Трансформувати у звичайну її можна з допомогою введення буфера.
З
2
Т
3
Д
2
З
1
Т
1
Д
1
Т
2
200
100
150
150
-
-
-
-
6
?
6
>
>
Z
Z
Z
Z~
Z
Z
Z
Z~
52
48
6
6
2
6
5
1
1
-
-
-
-
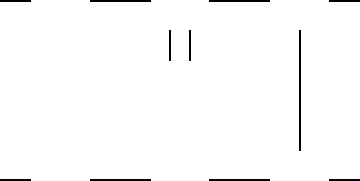
Рис. 1.14.1: Транспортна задача з трьома транзитними пунктами.
Розглянемо наступний приклад. Два автомобiльних заводи З
1
iЗ
2
зв’язанi iз двома дилерами Д
1
iД
2
, якi мають три транзитнi центри Т
1
,
Т
2
iТ
3
, як показано на рис. 1.14.1. Заводи З
1
iЗ
2
виготовляють 100 i 200
автомобiлiв. Замовлення дилерiв становлять по 150 автомобiлiв. Вартiсть
перевезення одного автомобiля (в сотнях доларiв США) показана на
рис. 1.14.1.
У данiй задачi перевезення транзитом можуть здiйснюватися через
довiльнi пункти (у вiдповiдностi до стрiлок на схемi), навiть через пункт
призначення Д
2
. Тому пункти, яким вiдповiдають як вхiднi, так i вихi-
днi стрiлки на схемi, назвемо транзитними (пункти Т
1
,Т
2
,Т
3
iД
2
).
Всi iншi будуть або iстинними пунктами вiдправлення (З
1
iЗ
2
), або
iстинними пунктами призначення (Д
1
). Цю модель можна перетворити
у звичайну транспортну модель з шiстьма пунктами вiдправлення (З
1
,
З
2
,Т
1
,Т
2
,Т
3
iД
2
) i п’ятьма пунктами призначення (Т
1
,Т
2
,Т
3
,Д
1
i
Д
2
). Об’єм попиту i пропозицiї, що вiдповiдає цим пунктам вiдправлення
i призначення, обчислюється за наступним правилом:
88
1. об’єм пропозицiї iстинного пункту вiдправлення = об’єм початкової
пропозицiї;
2. об’єм пропозицiї транзитного пункту = об’єм початкової пропозицiї
+об’ємбуфера;
3. об’єм попиту iстинного пункту вiдправлення = об’єм початкового
попиту;
4. об’єм попиту транзитного пункту = об’єм початкового попиту +
об’єм буфера.
Об’єм буфера
B має бути таким, щоб вмiстити об’єм загального по-
питу (чи пропозицiї). Тодi
B = 100 + 200 = 150 + 150 = 300.
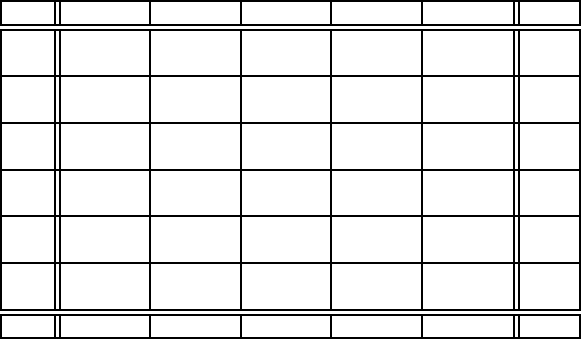
Побудована транспортна модель, еквiвалентна початковiй задачi, по-
казана в таблицi 1.14.1,
M – деяке велике число.
Табл.1.14.1
T
1
T
2
T
3
Д
1
Д
2
a
i
З
1
4 2 M M M
100
З
2
M 6 5 M M
200
T
1
0 1 M 8 M
B
T
2
1 0 M 6 5
B
T
3
M M 0 M 2
B
Д
2
M M M 6 0
B
b
j
B B B 150 150+B
Застосуємо метод Фогеля знаходження початкового розв’язку. Обчи-
слимо перший набiр штрафiв для рядкiв i стовпцiв.
Штрафи для рядкiв: З
1
: 4 − 2=2;З
2
: 6 − 5=1;Т
1
: 1 − 0=1;Т
2
:
1 − 0=1;Т
3
: 2 − 0=2;Д
2
: 6 − 0=6.
Штрафи для стовпцiв: Т
1
: 1 − 0=1;Т
2
: 1 − 0=1;Т
3
: 5 − 0=5;Д
1
:
6 − 6=0;Д
2
: 2 − 0=2.
Оскiльки рядок мiстить найбiльший штраф (6), i в цьому рядку най-
менша вартiсть перевезення знаходиться у клiтинцi (Д
2
,Д
2
), змiнну x
65
89
покладаємо рiвнiй 300 (див. таблицю 1.13.4). У цьому випадку повнiстю
виконується обмеження останнього рядка, його викреслюємо.
Обчислимо новий набiр перерахованих штрафiв.
Штрафи для рядкiв: З
1
: 4 − 2=2;З
2
: 6 − 5=1;Т
1
: 1 − 0=1;Т
2
:
1 − 0=1;Т
3
: 2 − 0=2;Д
2
: −.
Штрафи для стовпцiв: Т
1
: 1 − 0=1;Т
2
: 1 − 0=1;Т
3
: 5 − 0=5;Д
1
:
8 − 6=2;Д
2
: 5 − 2=3.
Найбiльший штраф (5) мiстить стовпець Т
3
, тому змiннiй x
53
,щоу
планi перевезень вiдповiдає клiтинцi (Т
3
,Т
3
), покладаємо значення 300.
У цьому випадку повнiстю виконуються обмеження як для рядка, так i
стовпця, але викреслюємо тiльки один з них, наприклад, стовпець Т
3
.
Пiсля чого знову перераховуємо штрафи.
Штрафи для рядкiв: З
1
: 4 − 2=2;З
2
: M − 6=M;Т
1
: 1 − 0=1;Т
2
:
1 − 0=1;Т
3
: M − 2=M −2;Д
2
: −.
Штрафи для стовпцiв: Т
1
: 1 −0=1;Т
2
: 1 −0=1;Т
3
: −;Д
1
: 8 −6=2;
Д
2
: 5 − 2=3.
Найбiльший штраф (
M − 2) вiдповiдає клiтинцi (Т
3
,Д
2
), x
55
=0.
Викреслюємо рядок Т
3
.
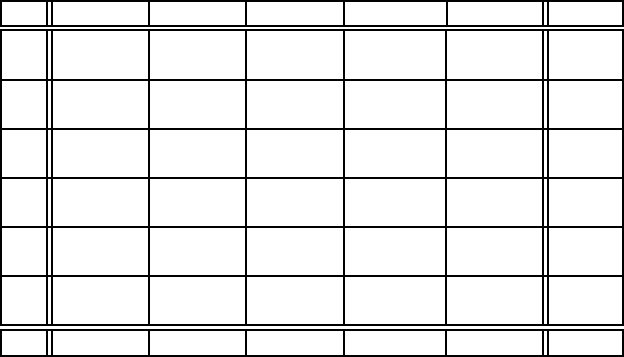
Табл.1.14.2
T
1
T
2
T
3
Д
1
Д
2
a
i
З
1
4 2
100
M M M
100
(7)
З
2
M 6
200
5 M M
200
(5)
T
1
0
300
1 M 8 M
300
(9)
T
2
1
0
0
0
M 6
150
5
150
300
(10)
T
3
M M 0
300
M 2
0
300
(3)
Д
2
M M M 6 0
300
300
(1)
b
j
300 300
(8)
300
(2)
150
(6)
450
(4)
Табл.1.14.3
90
