Моклячук М.П., Ямненко Р.Є. Лекції з теорії вибору та прийняття рішень (на укр. языке)
Подождите немного. Документ загружается.

Теорема 2.3.1. Основна теорема матричних iгор. Нехай гра визна-
чається матрицею виграшiв
A =(a
ij
)
m
i=1
n
j=1
розмiрностi m × n.Тодi
величини
max
X∈S
m
min
Y ∈S
n
E(X,Y ); min
Y ∈S
n
max
X∈S
m
E(X,Y )
iснують i рiвнi мiж собою
max
X∈S
m
min
Y ∈S
n
E(X,Y )= min
Y ∈S
n
max
X∈S
m
E(X,Y ).
Отже, кожна матрична гра має розв’язок у змiшаних стратегiях.
Кожний гравець у матричнiй грi завжди має оптимальну стратегiю.
Лема 2.3.1. Нехай задана матриця розмiрностi
m × n
A =
a
11
a
12
... a
1n
a
21
a
22
... a
2n
... ... ... ...
a
m1
a
m2
... a
mn
.
Тодi справедливе одне з двох тверджень:
1. Iснує елемент
X =(x
1
,...,x
m
) множини S
m
такий, що
a
1j
x
1
+ a
2j
x
2
+ ···+ a
mj
x
m
≥ 0,j=1,2,...,n;
2. Iснує елемент Y =(y
1
,...,y
n
) множини S
n
такий, що
a
i1
y
1
+ a
i2
y
2
+ ···+ a
in
y
n
≤ 0,i=1,2,...,m.
Доведення. Нехай
δ
(j)
=(δ
1j
,δ
2j
,...,δ
mj
),j=1,2,...,m,
де
δ
ij
=
0,i= j,
1,i= j,
−
символи Кронекера, точки простору R
m
, j-та координата яких дорiвнює
1, а всi iншi координати дорiвнюють нулю.
Нехай
a
(j)
=(a
1j
,a
2j
,...,a
mj
),j=1,2,...,n,−
точки простору R
m
, координати яких – це елементи j-го стовпчика ма-
трицi
A.ПозначимочерезC опуклу лiнiйну оболонку множини m + n
точок
δ
(1)
,...,δ
(m)
,a
(1)
,...,a
(n)
.
Нехай z =(0,...,0) – початок координат простору R
m
.Можливiдва
випадки:
z ∈ C; z ∈ C.Якщоz ∈ C,тоz є опуклою лiнiйною комбiнацiєю
точок
δ
(1)
,...,δ
(m)
,a
(1)
,...,a
(n)
.
111

Отже, iснує елемент (u
1
,...,u
m
,v
1
,...,v
n
) множини S
n+m
такий, що
u
1
δ
(1)
+ ···+ u
m
δ
(m)
+ v
1
a
(1)
+ ···+ v
n
a
(n)
= z. (2.3.1)
З рiвняння (2.3.1) випливає, що
u
1
δ
i1
+ ···+ u
m
δ
im
+ v
1
a
i1
+ ···+ v
n
a
in
=0,i=1,2,...,m,
або, з урахуванням визначення дельта-символiв,
u
i
+ v
1
a
i1
+ ···+ v
n
a
in
=0,i=1,2,...,m. (2.3.2)
Оскiльки
(u
1
,...,u
m
,v
1
,...,v
n
) ∈ S
n+m
, то u
i
невiд’ємнi i з рiвностi
(2.3.2) отримаємо
v
1
a
i1
+ ···+ v
n
a
in
≤ 0,i=1,2,...,m. (2.3.3)
Зауважимо тепер, що
v
1
+ ···+ v
n
> 0, (2.3.4)
бо в iншому випадку
v
1
= ···= v
n
=0,
i, як наслiдок рiвностi (2.3.2),
u
i
=0,i=1,2,...,m.
Ацесуперечитьтому,що(u
1
,...,u
m
,v
1
,...,v
n
) ∈ S
n+m
.
Покладемо
y
j
=
v
j
v
1
+ ···+ v
n
,j=1,2,...,n. (2.3.5)
З нерiвностей (2.3.3) i (2.3.4) ми маємо, що
y
1
a
i1
+ ···+ y
n
a
in
≤ 0,i=1,2,...,m.
З рiвностей (2.3.5) випливає, що (y
1
,...,y
n
) ∈ S
n
. Отже умова 2) леми
виконується.
Припустимо тепер, що
z ∈ C. Тодi за теоремою про опорну гiпер-
площину iснує гiперплощина, яка мiстить
z i така, що всi точки C
розташованi в одному з вiдповiдних пiвпросторiв. Нехай рiвняння цiєї
гiперплощини
b
1
t
1
+ ···+ b
m
t
m
= b
m+1
.
Оскiльки точка z лежить на гiперплощинi, то ми маємо
b
1
0+···+ b
m
0=b
m+1
.
Отже, b
m+1
=0. Таким чином, рiвняння гiперплощини має вигляд
b
1
t
1
+ ···+ b
m
t
m
=0. (2.3.6)
Ми можемо вважати, що будь-яка точка множини
C задовольняє нерiв-
нiсть
b
1
t
1
+ ···+ b
m
t
m
> 0. (2.3.7)
Нерiвнiсть (2.3.7) повинна бути справедливою, зокрема, для точок
δ
(1)
,
...,δ
(m)
множини C.Отже,
b
1
δ
1i
+ ···+ b
m
δ
mi
> 0,i=1,...,m. (2.3.8)
112

А це означає (вiдповiдно до визначення дельта-символiв), що
b
i
> 0,i=1,...,m. (2.3.9)
Нерiвнiсть (2.3.8) повинна бути справедливою, зокрема, для точок
a
(1)
,
...,a
(m)
множини C.Отже,
b
1
a
1i
+ ···+ b
m
a
mi
> 0,i=1,...,m. (2.3.10)
З нерiвностi (2.3.9) випливає, що
b
1
+···+b
m
> 0 i ми можемо визначити
x
i
=
b
i
b
1
+ ···+ b
m
,i=1,2,...,m. (2.3.11)
З виразiв (2.3.10) i (2.3.11) випливає, що
a
1j
x
1
+ a
2j
x
2
+ ···+ a
mj
x
m
> 0,j=1,2,...,n,
iтимбiльше
a
1j
x
1
+ a
2j
x
2
+ ···+ a
mj
x
m
≥ 0,j=1,2,...,n. (2.3.12)
Так як з виразiв (2.3.9) i (2.3.11) випливає, що
(x
1
,...,x
m
) ∈ S
m
,то
нерiвнiсть (2.3.12) означає, що умова 1) леми виконується.
Доведення. Доведемо основну теорему теорiї матричних iгор.
Для кожного
Y =(y
1
,...,y
n
) функцiя E(X,Y ) є неперевна лiнiйна
функцiя вiд
X =(x
1
,...,x
m
), яка визначена на замкнутiй пiдмножинi
S
m
простору R
m
.Тому
max
X∈S
m
E(X,Y )
iснує для кожного Y ∈ S
n
. Далi легко переконатися в тому, що
max
X∈S
m
E(X,Y )
є неперервною кусково-лiнiйною функцiєю вiд Y =(y
1
,...,y
n
),якави-
значена на
S
m
.ОскiлькиS
m
єзамкнутапiдмножинапросторуR
m
,то
min
Y ∈S
n
max
X∈S
m
E(X,Y )
iснує. Аналогiчно показується, що iснує
max
X∈S
m
min
Y ∈S
n
E(X,Y ).
Якщо перша умова леми 2.3.1 виконується, то iснує елемент X =
(x
1
,...,x
m
) множини S
m
такий, що
a
1j
x
1
+ a
2j
x
2
+ ···+ a
mj
x
m
≥ 0,j=1,2,...,n.
Тодi для довiльного Y ∈ S
n
E(X,Y )=
n
j=1
(a
1j
x
1
+ a
2j
x
2
+ ···+ a
mj
x
m
) y
j
≥ 0. (2.3.13)
Оскiльки спiввiдношення (2.3.13) справедливе для будь-якого
Y ∈ S
n
,
то
min
Y ∈S
n
E(X,Y ) ≥ 0.
113

Отже,
max
X∈S
m
min
Y ∈S
n
E(X,Y ) ≥ 0. (2.3.14)
Аналогiчно показуємо, що
min
Y ∈S
n
max
X∈S
m
E(X,Y ) ≤ 0, (2.3.15)
якщо виконуєтьс умова 2) леми 2.3.1.
Оскiльки виконується або умова 1), або умова 2) леми 2.3.1, то при-
наймнi одна з двох нерiвностей, (2.3.14) чи (2.3.15), повинна виконува-
тися, i, отже, нерiвнiсть
max
X∈S
m
min
Y ∈S
n
E(X,Y ) < 0 < min
Y ∈S
n
max
X∈S
m
E(X,Y ) (2.3.16)
не може бути справедливою.
Нехай
A
k
– матриця, яку отримаємо з матрицi A при вiднiманнi k вiд
кожного елемента, тобто
A
k
=
a
11
− ka
12
− k ... a
1n
− k
a
21
− ka
22
− k ... a
2n
− k
... ... ... ...
a
m1
− ka
m2
− k ... a
mn
− k
,
iнехайE
k
(X,Y ) – це математичне сподiвання виграшу у грi з матрицею
A
k
:
E
k
(X,Y )=
m
i=1
n
j=1
(a
ij
− k)x
i
y
j
= E(X,Y ) − k.
Тодi, точно так само, як ми показали, що нерiвнiсть (2.3.16) не викону-
ється для
A, ми можемо показати, що нерiвнiсть
max
X∈S
m
min
Y ∈S
n
E
k
(X,Y ) < 0 < min
Y ∈S
n
max
X∈S
m
M
k
(X,Y )
не виконується для A
k
. Отже, нерiвнiсть
max
X∈S
m
min
Y ∈S
n
M(X,Y ) <k<E(X,Y ) <k< min
Y ∈S
n
max
X∈S
m
M(X,Y )
неправильна для всiх чисел k. А тому не виконується нерiвнiсть
max
X∈S
m
min
Y ∈S
n
E(X,Y ) < min
Y ∈S
n
max
X∈S
m
E(X,Y ).
Тому справедлива нерiвнiсть
max
X∈S
m
min
Y ∈S
n
E(X,Y ) ≥ min
Y ∈S
n
max
X∈S
m
E(X,Y ).
З iншого боку за теоремою 2.2.1
max
X∈S
m
min
Y ∈S
n
E(X,Y ) ≤ min
Y ∈S
n
max
X∈S
m
E(X,Y ).
Азначить,
max
X∈S
m
min
Y ∈S
n
E(X,Y )= min
Y ∈S
n
max
X∈S
m
E(X,Y ).
Це i завершує доведення теореми.
114

2.4. ВЛАСТИВОСТI ОПТИМАЛЬНИХ СТРАТЕГIЙ ГРИ
Теорема 2.4.1. Нехай v –дiйснечислотаX
∗
, Y
∗
– елементи множин
S
n
та S
m
вiдповiдно. Для того, щоб v було цiною гри, а X
∗
, Y
∗
були оптимальними стратегiями першого та другого гравцiв гри з
матрицею
A =(a
ij
)
m
i=1
n
j=1
, необхiдно i достатньо, щоб для всiх i :1≤
i ≤ m
,тадлявсiхj :1≤ j ≤ n, виконувались нерiвностi
E
(i,Y
∗
) ≤ v ≤ E(X
∗
,j).
Тут через E(i,Y ) позначено виграш першого гравця за умови, що вiн
застосовує свою чисту
i-ту стратегiю, а другий гравець застосовує
стратегiю
Y : E(i,Y )=
n
j=1
a
ij
y
j
. Аналогiчно E(X,j)=
m
i=1
x
i
a
ij
.
Доведення. Необхiднiсть умови випливає безпосередньо з визначення
сiдлової точки. З iншого боку, якщо умова виконується, то для будь-
якого елементу
X =(x
1
,...,x
m
) множини S
m
m
i=1
E(i,Y
∗
)x
i
≤
m
i=1
vx
i
= v.
Отже,
E
(X,Y
∗
) ≤ v. (2.4.1)
Аналогiчно, для будь-якого елементу
Y =(y
1
,...,y
n
) множини S
n
v ≤ E(X
∗
,Y ). (2.4.2)
З нерiвностей (2.4.1) i (2.4.2) при замiнi
X на X
∗
та Y на Y
∗
маємо
E
(X
∗
,Y
∗
) ≤ v ≤ E(X
∗
,Y
∗
). (2.4.3)
Азначить,
E
(X
∗
,Y
∗
)=v.
З нерiвностей (2.4.1), (2.4.2), (2.4.3) матимемо для всiх X ∈ S
m
та всiх
Y ∈ S
n
E(X,Y
∗
) ≤ E(X
∗
,Y
∗
) ≤ E(X
∗
,Y ).
Отже, (X
∗
,Y
∗
) єсiдловоюточкоюфункуцiїE(X,Y ),аv єцiноюгри.
Теорема 2.4.2. Нехай (X
∗
,Y
∗
) – розв’язок гри з матрицею A розмiр-
ностi
m × n.Тодi
max
1≤i≤m
E(i,Y
∗
)= min
1≤j≤n
E(X
∗
,j)=E(X
∗
,Y
∗
).
Доведення. За попередньою теоремою для всiх 1 ≤ j ≤ n має мiсце
нерiвнiсть
v ≤ E(X
∗
,j),
115

де v –цiнагри.Тодi
v ≤ min
1≤j≤n
E(X
∗
,j).
Якщо
v< min
1≤j≤n
E(X
∗
,j),
то для всiх 1 ≤ j ≤ n
v<
E(X
∗
,j).
Тодi
v<E(X
∗
,Y
∗
).
Ацесуперечитьтому,щоv цiна гри. Отже,
v =min
1≤j≤n
E(X
∗
,j).
Аналогiчно показується, що
v =max
1≤i≤m
E(i,Y
∗
).
Наступна теорема часто виявляється дуже корисною при вiдшуканнi
розв’язкiв гри.
Теорема 2.4.3. Нехай
X
∗
=(x
∗
1
,...,x
∗
m
), Y
∗
=(y
∗
1
,...,y
∗
n
) – розв’язок
гри з матрицею
A розмiрностi m ×n i нехай цiна гри дорiвнює v.Тодi
для будь-якого
i, при якому E(i,Y
∗
) <v,маємiсцерiвнiстьx
∗
i
=0,а
для будь-якого
j, при якому E(X
∗
,j) >v,маємiсцерiвнiстьy
∗
j
=0.
Доведення. Припустимо, що для деякого
i
0
E(i
0
,Y
∗
) <v
i x
∗
i
o
=0. Тодi ми маємо, що
E
(i
0
,Y
∗
)x
∗
i
0
<vx
∗
i
0
.
Оскiльки для i = i
0
E(i,Y
∗
) ≤ v,
то
E
(i,Y
∗
)x
∗
i
≤ vx
∗
i
.
Отже, матимемо
m
i=1
E(i,Y
∗
)x
i
<
m
i=1
vx
i
i
E
(X
∗
,Y
∗
) <v,
що суперечить умовi, що v – це цiна гри. Друга частина теореми дово-
диться аналогiчно.
116
Теорема 2.4.4. Нехай E – математичне сподiвання виграшу першо-
го гравця у грi з матрицею
A розмiрностi m × n iнехайX
∗
, Y
∗
–
елементи множин
S
m
та S
n
вiдповiдно. Тодi мають мiсце наступнi
еквiвалентнi твердження:
1.
X
∗
є оптимальною стратегiєю першого гравця, а Y
∗
єопти-
мальною стратегiєю другого гравця.
2. Якщо
X – це довiльний елемент множини S
m
,аY – довiльний
елемент множини
S
n
,то
E
(X,Y
∗
) ≤ E(X
∗
,Y
∗
) ≤ E(X
∗
,Y ).
3. Якщо i та j – це будь-якi цiлi числа, такi, що 1 ≤ i ≤ m,
1 ≤ j ≤ n,то
E
(i,Y
∗
) ≤ E(X
∗
,Y
∗
) ≤ E(X
∗
,j).
2.5. СПРОЩЕННЯ МАТРИЧНИХ IГОР
Означення 2.5.1. Вектор a =(a
1
,...,a
n
) домiнує вектор b =(b
1
, ...,b
n
),
якщо
a
i
≥ b
i
для всiх 1 ≤ i ≤ n.Якщоa
i
>b
i
для всiх 1 ≤ i ≤
n
, то говорять, що вектор a =(a
1
,...,a
n
) строго домiнує вектор b =
(b
1
,...,b
n
).
Означення 2.5.2.Розширеннястратегiї
X
=(x
1
,...,x
n
) ∈ S
n
на i-ому
мiсцi – це вектор
X =(x
1
,...,x
i−1
,0,x
i
,...,x
n
) ∈ S
n+1
.
Теорема 2.5.1. Нехай
G –гразматрицеюA.Нехайi-й рядок матри-
цi
A домiнує деяка опукла лiнiйна комбiнацiя iнших рядкiв матрицi
A.НехайграG
зматрицеюA
, яка отримана iз матрицi A пiсля
виключення
i-го рядка. Тодi цiна гри G
дорiвнює цiнi гри G.Опти-
мальна стратегiя другого гравця у грi
G
єоптимальноюстратегiєю
другого гравця у грi
G.ЯкщоX
–оптимальнастратегiяпершого
гравця у грi
G
i X – це розширення X
на i-тому мiсцi, то X бу-
де оптимальною стратегiєю першого гравця у грi
G.Далi,якщоi-й
рядок матрицi
A строго домiнує деяка опукла лiнiйна комбiнацiя iн-
ших рядкiв, то будь-який розв’язок гри
G можна отримати вказаним
способом iз розв’язку гри
G
.
Доведення. Нехай задана матриця порядку
m × n
A =
a
11
a
12
... a
1n
a
21
a
22
... a
2n
... ... ... ...
a
m1
a
m2
... a
mn
.
117
Можна припустити, що останнiй рядок матрицi A перевищує опукла
лiнiйна комбiнацiя iнших рядкiв. Тому iснує елемент
z =(z
1
,...,z
m−1
)
множини S
m−1
такий, що
a
mj
≤
m−1
i=1
a
ij
z
i
,j=1,2,...,n. (2.5.1)
Нехай
v –цiнагриG
i w =(w
1
,...,w
m−1
) –оптимальнастратегiя
першого гравця у грi
G
,аy =(y
1
,...,y
n
) – оптимальна стратегiя гравця
другого гравця у грi
G
. Тодi за теоремою 2.4.1
n
j=1
a
ij
y
j
≤ v, i =1,2,...,m− 1; (2.5.2)
v ≤
m−1
i=1
a
ij
w
i
,j=1,2,...,n. (2.5.3)
Для доведення першої частини теореми досить показати, що
v єта-
кож цiна гри
G, y =(y
1
,...,y
n
) – оптимальна стратегiя гравця другого
гравця у грi
G,iw =(w
1
,...,w
m−1
,0) – оптимальна стратегiя першого
гравця у грi
G.
З попереднiх теорем випливає, що для цього потрiбно довести спра-
ведливiсть наступних нерiвностей:
n
j=1
a
ij
y
j
≤ v, i =1,2,...,m; (2.5.4)
v ≤
m−1
i=1
a
ij
w
i
+ a
mj
0,j=1,2,...,n. (2.5.5)
Нерiвнiсть (2.5.5) – це очевидний наслiдок нерiвностi (2.5.3). Тому до-
сить довести нерiвнiсть (2.5.4). Отже, користуючись нерiвнiстю (2.5.2),
досить показати, що
n
j=1
a
mj
y
j
≤ v. (2.5.6)
З нерiвностей (2.5.1), (2.5.2) маємо
n
j=1
a
mj
y
j
≤
n
j=1
m−1
i=1
a
ij
z
i
y
j
≤
m−1
i=1
n
j=1
a
ij
y
j
z
i
≤
m−1
i=1
vz
i
= v,
що i доводить справедливiсть теореми. Для доведення другої частини
теореми зауважимо, що якщо у жодному зi спiввiдношень (2.5.1) немає
118

рiвностi, то
n
j=1
a
mj
y
j
<
n
j=1
m−1
i=1
a
ij
z
i
y
j
≤ v.
Отже, за теоремою 2.4.3 кожна оптимальна стратегiя першого гравця
буде мати нульову
m-ту компоненту.
Доведення наступної теореми аналогiчне.
Теорема 2.5.2. Нехай
G –гразматрицеюA.Нехайj-й стовпчик ма-
трицi
A домiнує деяку опуклу лiнiйну комбiнацiю iнших стовпчикiв
матрицi
A.НехайG
–гразматрицеюA
, яка отримана iз матрицi
A пiсля виключення j-го стопчика. Тодi цiна гри G
дорiвнює цiнi гри
G. Оптимальна стратегiя першого гравця у грi G
єоптимальною
стратегiєю першого гравця у грi
G.ЯкщоY
–оптимальнастрате-
гiя другого гравця у грi
G
i Y – це розширення Y
на j-тому мiсцi, то
Y буде оптимальною стратегiєю другого гравця у грi G.Далi,якщо
j-й стовпчик матрицi A строго домiнує деяку опуклу лiнiйну комбi-
нацiю iнших рядкiв, то будь-який розв’язок гри
G можна отримати
вказаним способом iз розв’язку гри
G
.
Наведемо приклад застосування цих теорем.
Приклад 2.5.1. Нехай гра задана матрицею
3240
3424
4240
0408
.
Оскiльки третiй рядок матрицi домiнує перший, то, викреслюючи пер-
шийрядок,миодержуємо:
3424
4240
0408
.
У новiй матрицi перший стовпець домiнує третiй; викреслюючи перший
стовпець, ми одержуємо:
424
240
408
.
У цiй матрицi нiякий рядок (i нiякий стовпець) не домiнує iншi рядки
(i стовпцi). Але перший стовпець домiнує опуклу лiнiйну комбiнацiю
другого i третього стовпцiв, тому що
4 >
1
2
× 2+
1
2
× 2,
119
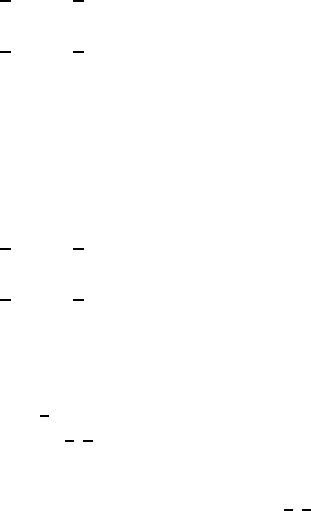
2=
1
2
× 4+
1
2
× 0,
4=
1
2
× 0+
1
2
× 8.
Тому ми виключаємо перший стовпець i одержуємо:
24
40
08
.
У свою чергу в цiй матрицi опукла лiнiйна комбiнацiя другого i третього
рядкiв домiнує перший рядок
2=
1
2
× 4+
1
2
× 0,
4=
1
2
× 0+
1
2
× 8.
Таким чином, наша матриця приведена до матрицi
40
08
.
Цiна гри з цiєю матрицею дорiвнює
8
3
, а оптимальна стратегiя для першо-
го гравця (i для другого гравця) буде
(
2
3
,
1
3
). Отже, оскiльки ми одержали
матрицю
2 × 2 зматрицi4 × 4,викреслюючипершiдварядкиiпершi
два стовпчики, то приходимо до висновку, що оптимальна стратегiя для
першого гравця (i для другого гравця) у початковiй грi є
(0,0,
2
3
,
1
3
).
Зауваження. Iз доведених теорем випливає, що коли ми викреслюємо
рядок (чи стовпець), який домiнується строго, то ми одержуємо матри-
цю, що приводить до точно такої системи розв’язкiв, яку б ми отримали,
розв’язавшипочатковугру.Однакценевiрноутомувипадку,колиспiв-
вiдношення переваги не є строгим; у цьому випадку ми можемо втратити
деякi з розв’язкiв початкової гри.
Приклад 2.5.2. Як приклад розглянемо гру з матрицею виграшiв
00 0
01−1
0 −11
.
Легко переконатися в тому, що будь-який елемент множини S
3
вигляду
(a,b,b) буде оптимальною стратегiєю для першого гравця. З iншого боку,
якщо ми викреслимо перший рядок (який домiнує, але не строго, опу-
кла лiнiйна комбiнацiя двох iнших рядкiв) i потiм викреслимо перший
стовпець,томиодержимоматрицю
1 −1
−11
,
120
