Моклячук М.П., Ямненко Р.Є. Лекції з теорії вибору та прийняття рішень (на укр. языке)
Подождите немного. Документ загружается.


d
1
d
2
d
3
w
1
0 10 4
w
2
8 0 3
L (w,d) задається формулою
L (w,d) = 100 (w − d)
2
.
Припустимо, що щiльнiсть розподiлу ймовiрностей P параметра W
визначається рiвнiстю
p (w)=2w, 0 ≤ w ≤ 1.
Покажiть, що d =2/3 є байєсiвським рiшенням при такому розподiлi
P i що байєсiвский ризик дорiвнює 50/9.
3. Розглянемо задачу прийняття рiшень з прикладу 3.2.1, але припу-
стимо тепер, що функцiя втрат L(w,d) замiнена новою функцiєю
втрат L
0
(w,d). Вона задається таблицею нижче. Покажiть, що при
будь-якому розподiлi параметра W байєсiвське рiшення для функцiї
втрат L
0
(w,d) збiгається з байєсiвським рiшенням для функцiї втрат
L(w,d).
d
1
d
2
d
3
w
1
4 6 7
w
2
0 − 1 1
w
3
0 1 −3
w
4
1 2 0
4. Нехай у задачi прийняття рiшень d
∗
є байєсiвським рiшенням для
двох рiзних розподiлiв P
1
i P
2
параметра W .Доведiть,щотодiдля
будь-якого числа α, 0 <α<1, d
∗
є байєсiвським рiшенням для
розподiлу αP
1
+(1− α) P
2
.
5. Розглянемо задачу прийняття рiшень 2. Припустимо, що статистик
A вважає, що щiльнiсть розподiлу ймовiрностей параметра W є
p (w)=2w, 0 ≤ w ≤ 1,астатистикB упевнений в тому, що щiль-
нiсть розподiлу ймовiрностей для W єфункцiяp
B
,яказадається
формулою
p
B
(w)=3w
2
, 0 ≤ w ≤ 1.
Який додатковий ризик має статистик A з точки зору статистика B
через неправильний вибiр розподiлу W ?
201
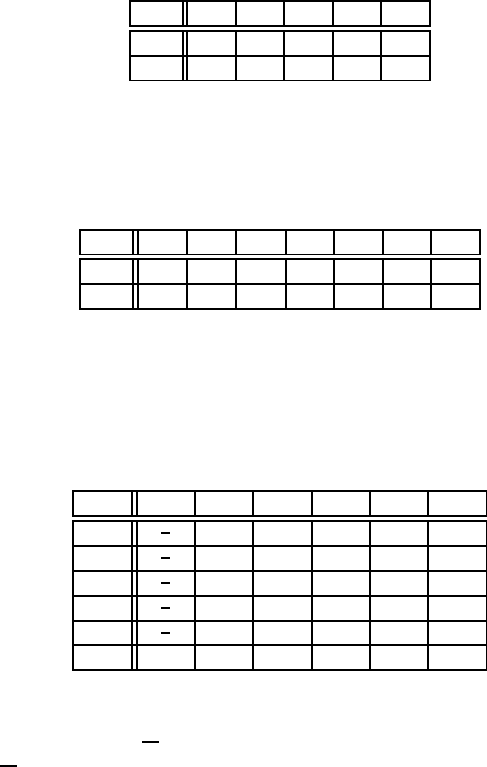
6. Розглянемо задачу прийняття рiшень, де Ω={w
1
,w
2
}, D = {d
1
,...,d
5
}
iфункцiявтратL(w,d) задана таблицею нижче. При якому розподiлi
параметра W байєсiвське рiшення не єдине?
d
1
d
2
d
3
d
4
d
5
w
1
0 4 2 1 5
w
2
4 5 0 1 0
7. Розглянемо задачу прийняття рiшень, у якiй Ω={w
1
,w
2
}, D =
{d
1
,...,d
7
} iфункцiявтратL(w,d) задається таблицею нижче. Зна-
йдiть всi байєсiвськi рiшення для кожного розподiлу P параметра
W .
d
1
d
2
d
3
d
4
d
5
d
6
d
7
w
1
1 6 0 2 7 3 4
w
2
10 1 13 8 0 5 4
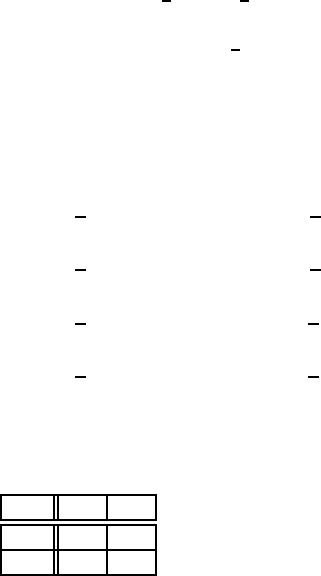
8. Розглянемо задачу прийняття рiшень, у якiй обидвi множини Ω i D
складаються iз злiченої нескiнченної кiлькостi елементiв. Нехай Ω=
{w
1
,w
2
,...}, D = {d
∗
,d
1
,d
2
,...},афункцiяL задається таблицею
нижче. Доведiть, що d
∗
є єдиним допустимим рiшенням у D,алеце
рiшення не є байєсiвським нi при якому розподiлi параметра W .
d
∗
d
1
d
2
d
3
d
4
...
w
1
1
2
0 0 0 0 ...
w
2
1
2
1 0 0 0 ...
w
3
1
2
1 1 0 0 ...
w
4
1
2
1 1 1 0 ...
w
5
1
2
1 1 1 1 ...
... ... ... ... ... ... ...
9. Припустимо, що ймовiрнiсть наявностi деякого сигналу в данiй си-
стемi дорiвнює
1
10
, а ймовiрнiсть того, що сигналу немає, дорiвнює
9
10
. Нехай вимiри над системою у випадку наявностi сигналу роз-
подiленi нормально iз середнiм 50 i мiрою точностi 1, а вимiри при
вiдсутностi сигналу також нормально розподiленi, але iз середнiм 52
i мiрою точностi 1. Нехай, далi, x є результат вимiру в деякий мо-
мент часу. Покажiть, що апостерiорна ймовiрнiсть наявностi сигналу
202
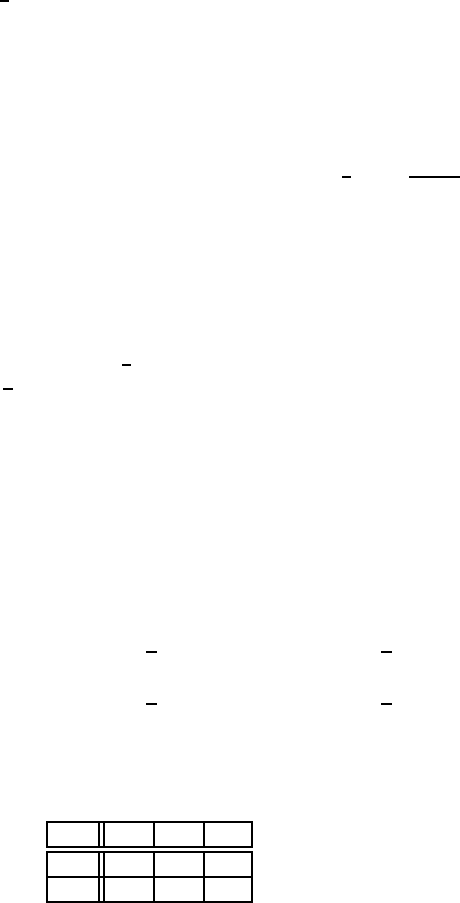
бiльше апостерiорної ймовiрностi його вiдсутностi тодi i лише тодi
коли x<51 −
1
2
log 9.
10. Розглянемо задачу прийняття рiшень, у якiй Ω={w
1
,w
2
}, D =
{d
1
,d
2
} iфункцiявтратL задається таблицею 3.7.1. Припустимо,
що статистик може спостерiгати випадкову величину Z, умовний
розподiл якої при W = w
1
нормальний iз середнiм 0 i дисперсiєю
1, а при W = w
2
– нормальний iз середнiм 1 i дисперсiєю 1. Для
будь-якої заданої апрiорної ймовiрностi p = P (W = w
1
) нехай δ –
така вирiшуюча функцiя, що δ (z)=d
1
,якщоz<
1
2
+log
p
2(1−p)
,i
δ (z)=d
2
впротилежномувипадку.
(а) Покажiть, що δ є байєсiвським рiшенням при такиму розподiлi
p.
(б) Як виглядає графiк байєсiвського ризику на iнтервалi 0 ≤ p ≤ 1?
11. Припустимо, що статистик має зробити висновок про те, чи деяка ве-
личина рiвномiрно розподiлена на iнтервалi (0,1),чивонарiвномiрно
розподiлена на iнтервалi
0,
1
2
. Ймовiрнiсть кожної з цих можливо-
стей дорiвнює
1
2
. Нехай збиток вiд прийняття правильного рiшення
дорiвнює 0, а якщо прийняте невiрне рiшення, то збиток дорiвнює
a>0. Доведiть, що якщо статистик може вибирати число спостере-
жень над випадковою величиною, причому цiна кожного спостере-
ження дорiвнює c>0, то йому варто робити n
∗
спостережень, де n
∗
– невiд’ємне цiле число, яке мiнiмiзує значення a2
−(n+1)
+ nc.
12. Розглянемо задачу прийняття рiшень, у якiй Ω={w
1
,w
2
}, D =
{d
1
,d
2
,d
3
} афункцiявтратL(w,d) задається таблицею нижче. При-
пустимо, що нам доступне спостереження випадкової величини X з
наступними умовними розподiлами:
P ( X =1|W = w
1
)=
3
4
, P (X =0|W = w
1
)=
1
4
;
P ( X =1|W = w
2
)=
1
4
, P (X =0|W = w
2
)=
3
4
.
Нехай p = P (W = w
1
). Визначте для кожного значення p (0 ≤ p ≤ 1)
байєсiвську вирiшуючу функцiю i побудуйте графiк байєсiвського
ризику ρ
∗
(ξ) як функцiї вiд p.
d
1
d
2
d
3
w
1
0 10 3
w
2
10 0 3
203

13. Припустимо, що в умовах задачi 12 статистик перед прийняттям рi-
шення може спостерiгати значення випадкових величин X
1
,...,X
n
,
якi при кожному даному значеннi W = w
i
(i =1,2) незалежнi i
однаково розподiленi з X. Для довiльного об’єму вибiрки n знайдiть
байєсiвську вирiшуючу функцiю при кожному значеннi p.
14. Нехай в умовах задач 12 i 13 p =
1
2
iцiнаc кожного спостереження
дорiвнює
1
10
. Покажiть, що оптимальний об’єм вибiрки n дорiвнює 8
i мiнiмум загального ризику дорiвнює 1.33.
15. Припустимо, що в умовах задач 12 i 13 цiна кожного спостереже-
ння залежить вiд його результату: спостереження, що дає значення
1, коштує 0.15, а кожне спостереження, що дає значення 0, коштує
0.05. Покажiть, що при p =
1
2
оптимальний об’єм вибiрки i мiнiмаль-
ний загальний ризик збiгається з вiдповiдними величинами з задачi
14.
16. Розглянемо задачу прийняття рiшень, у якiй Ω={w
1
,w
2
}, D =
{d
1
,d
2
} iфункцiявтратL(w,d) задається таблицею 16 нижче. Нехай
P (W = w
1
)=P (W = w
2
)=
1
2
i умовний розподiл спостереження
X при W = w
1
нормальний iз середнiм −1 i дисперсiєю 9, а при
W = w
2
– нормальний iз середнiм 1 i дисперсiєю 9. Припустимо,
що перед прийняттям рiшення статистик може спостерiгати значе-
ння випадкових величин X
1
,...,X
n
,якiприбудь-якомузаданому
значеннi W незалежнi i однаково розподiленi з X.Покажiть,що
якщо кожне спостереження у вибiрцi коштує 1, те оптимальний об’-
єм вибiрки n дорiвнює 42, а мiнiмальний повний ризик дорiвнює
57.4.
d
1
d
2
w
1
0 1000
w
2
1000 0
17. Розглянемо k випадкових величин X
1
,...,X
k
. Припустимо, що щiль-
нiсть розподiлу ймовiрностей однiєї з цих випадкових величин дорiв-
нює g, а щiльнiсть розподiлу ймовiрностей всiх iнших k −1 випадко-
вих величин рiвнi h, але яка саме з випадкових велич має щiльнiсть
g,невiдомо.Приi =1,...,k нехай p
i
позначає апрiорну ймовiрнiсть
того, що X
i
– випадкова величина з щiльнiстю розподiлу ймовiрно-
стей g.Тутp
i
> 0, i =1,...,k i
k
i=1
p
i
=1.
204
а) Припустимо, що спостерiгається випадкова величина X
1
,значен-
ня якої виявилося рiвним x. Знайдiть апостерiорну ймовiрнiсть того,
що щiльнiсть розподiлу ймовiрностей X
1
є g.
б) Припустимо, що спостереження випадкової величини X
3
дало
значення x. Визначите апостерiорну ймовiрнiсть того, що щiльнiсть
розподiлу ймовiрностей X
1
є g.
18. Розглянемо два ящики A i B, кожен з який мiстить червонi i зеленi
кулi. Вiдомо, що в одному з ящикiв половина всiх куль червонi, а
iншi кулi зеленi. В iншому ящику чверть усiх куль червонi, а три
чвертi куль зеленi. Нехай ящик, де половина куль червонi, позна-
чений через W , причому невiдомо, W = A чи W = B.Нехайдалi,
P (W = A)=p i P (W = B)=1− p,деp –заданечисло,0 <p<1.
Припустимо, що статистик може вибрати навмання одну кулю з ящи-
ка A чи B i пiсля цього спостереження повинний прийняти рiшення
W = A чи W = B.Покажiть,щоякщо
1
2
<p<
2
3
,тодлятогощоб
максимiзувати ймовiрнiсть правильного рiшення йому варто вийня-
ти кулю з ящика B. Покажiть, далi, що якщо
2
3
≤ p ≤ 1,тевибiр
ящика несуттєвий.
19. Розглянемо задачу прийняття рiшень, у якiй Ω={w
1
,w
2
}, D =
{d
1
,d
2
} iфункцiявтратL задана таблицею нижче. Нехай статистик
може спостерiгати або величину X, або величину Y з наступними
умовними розподiлами:
P ( X =1|W = w
1
)=
2
3
, P (X =0|W = w
1
)=
1
3
,
P ( X =1|W = w
2
)=
1
2
, P (X =0|W = w
2
)=
1
2
,
P ( Y =1|W = w
1
)=
3
4
, P (Y =0|W = w
1
)=
1
4
,
P ( Y =1|W = w
2
)=
1
2
, P (Y =0|W = w
2
)=
1
2
.
Припустимо, що цiни спостережень X i Y однаковi. Покажiть, що
для будь-якого апрiорного розподiлу W iдлявсiхзначеньзбиткiв
a
1
i a
2
статистику слiд вiддати перевагу спостереженню Y .
d
1
d
2
w
1
0 a
1
w
2
a
2
0
205

20. Нехай W – параметр, що приймає два значення w
1
i w
2
з апрiорними
ймовiрностями P (W = w
1
)=p i P (W = w
2
)=1− p.Припустимо,
що ми маємо спостереження X зумовноющiльнiстюрозподiлуймо-
вiрностей f ( ·|w
i
), i =1,2.Черезp (x) позначимо апостерiорну ймо-
вiрнiсть того, що W = w
1
,колиX = x.Покажiть,щоE [p (X)] = p,
де математичне сподiвання обчислюється за припущення, що W має
зазначений апрiорний розподiл.
21. Якщо в умовах задачi 20 припустити, що W = w
1
,тоE [p (X)] ≥ p.
Зауваження. Цю задачу можна iнтерпретувати як твердження про
те, що в середньому апостерiорний розподiл приписує правильному
значенню W бiльшу ймовiрнiсть, нiж апрiорний.
22. В умовах задачi 20 нехай апрiорний розподiл W такий, що p =1−
p =
1
2
.Припускаючи,щоW = w
1
, доведiть, що при всiх ε (0 <ε<1)
P [p (X) ≤ ε] ≤
ε
1 − ε
.
Зауваження. Цю задачу можна iнтерпретувати як твердження про
те, що апостерiорний розподiл припише iстинному значенню W малу
ймовiрнiсть лише з малою ймовiрнiстю.
23. Розглянемо множину Ω={w
1
,w
2
,w
3
}, що складається з трьох точок,
iсiмействоP усiх ймовiрнысних розподiлiв (p
1
,p
2
,p
3
) на Ω таких, що
p
i
≥ 0(i =1,2,3) i p
1
+ p
2
+ p
3
=1.НехайΨ – множина усiх то-
чок (як внутрiшнiх, так i граничних) рiвностороннього трикутника
з одиничною висотою. Нехай v
1
,v
2
,v
3
– вершини цього трикутника i
S
i
при i =1,2,3 позначає сторону трикутника, протилежну вершинi
v
i
. Як легко бачити, сума вiдстаней вiд будь-якої точки трикутника
до трьох його сторiн дорiвнює 1. Покажiть, що iснує взаємно одно-
значна вiдповiднiсть мiж множинами P i Ψ,приякомукожнiйточцi
(p
1
,p
2
,p
3
) ∈ P вiдповiдає точка x ∈ Ψ, вiдстань якої вiд сторони S
i
дорiвнює p
i
(i =1,2,3).
206
Роздiл IV
Спряженi апрiорнi розподiли
4.1. ДЕЯКI НАЙБIЛЬШ ТИПОВI РОЗПОДIЛИ
Дамо означення та вкажемо властивостi деяких найбiльш типових роз-
подiлiв, якi використовуються в наступних роздiлах.
Розподiл Бернуллi. Дискретна випадкова величина X має розподiл
Бернуллi з параметром p (0 <p<1),якщоX приймає лише два значе-
ння 1 та 0 вiдповiдно з ймовiрностями p та q =1− p. Функцiю розподiлу
ймовiрностей можна записати у виглядi
f(x|p)=
p
x
q
1−x
, коли x =0,1,
0, в iнших випадках.
(4.1.1)
Якщо випадкова величина X має розподiл Бернуллi (4.1.1), то
E(X)=p, Var (X)=pq. (4.1.2)
Якщо всi випадковi величини скiнченної або нескiнченної послiдовностi є
незалежними та мають той же самий розподiл Бернуллi, то маємо послi-
довнiсть випробувань Бернуллi.
Бiномiальний розподiл. Дискретна випадкова величина X має бiно-
мiальний розподiл з параметрами n, p (n =1,2,...;0<p<1),якщоX
приймає значення x =0,1,2,...,n зймовiрностями
f(x|n,p)=
n
x
p
x
q
1−x
, коли x =0,1,2,...,n
0, в iнших випадках.
(4.1.3)
Якщо X
1
,X
2
,...,X
n
– послiдовнiсть випробувань Бернуллi з параметром
p,тосумаX
1
+ X
2
+ ··· + X
n
випадкових величин має бiномiальний
розподiл з параметрами n, p.
Якщо випадкова величина X має бiномiальний розподiл (4.1.3) з пара-
метрами n, p,то
E(X)=np, Var (X)=npq. (4.1.4)
Якщо випадковi величини X
1
,X
2
,...,X
k
незалежнi и мають бiномiаль-
ний розподiл з параметрами n
i
, p,тосумаX
1
+ X
2
+ ···+ X
k
випадкових
величин має бiномiальний розподiл з параметрами n
1
+ n
2
+ ···+ n
k
та p.
Розподiл Пуассона. Дискретна випадкова величина X має розподiл
Пуассона з середнiм значенням λ (λ>0), якщо функцiю розподiлу ймо-
207

вiрностей можна записати у виглядi
f(x|λ)=
λ
x
x!
e
−λ
, коли x =0,1,2,...
0, в iнших випадках.
(4.1.5)
Якщо випадкова величина X має розподiл Пуассона (4.1.5), то
E(X)=λ, Var(X)=λ. (4.1.6)
Якщо випадковi величини X
1
,X
2
,...,X
n
незалежнi i мають розподiл
Пуассона з параметрами λ
i
,i =1,2,...,n,тосумаX
1
+ X
2
+ ··· + X
n
випадкових величин має розподiл Пуассона з параметром λ
1
+λ
2
+···+λ
k
.
Вiд’ємний бiномiальний розподiл. Дискретна випадкова величина X
має вiд’ємний бiномiальний розподiл з параметрами r, p (r>0; 0 <p<
1), якщо її функцiя розподiлу ймовiрностей має вигляд
f(x|r,p)=
r+x−1
x
p
r
q
1−x
, коли x =0,1,2,...
0, в iнших випадках.
(4.1.7)
Вiд’ємний бiномiальний розподiл при натуральних r можна отримати на-
ступним чином. Нехай в послiдовностi випробувань Бернуллi з параме-
тром p величина Y позначає число випробувань, якi провели до того, як
значення 1 отримати r раз. Якщо X – це число випробувань, при яких
з’явився 0, перш нiж одиниця з’явилась r раз, то X = Y − r iцяве-
личина X має вiд’ємний бiномiальний розподiл з параметрами r, p.При
r =1вiд’ємний бiномiальний розподiл часто називають геометричним
розподiлом.
Якщо випадкова величина X має вiд’ємний бiномiальний розподiл
(4.1.7) з параметрами r, p,то
E(X)=
rq
p
, Var(X)=
rq
p
2
. (4.1.8)
Якщо випадковi величини X
1
,X
2
,...,X
k
незалежнi i мають вiд’ємний
бiномiальний розподiл з параметрами r
i
, p,тосумаX
1
+ X
2
+ ···+ X
k
випадкових величин має вiд’ємний бiномiальний розподiл з параметрами
зпараметрамиr
1
+ r
2
+ ···+ r
k
, p.
Гiпергеометричний розподiл. Дискретна випадкова величина X має
гiпергеометричний розподiл з параметрами A, B, n, n ≤ A + B,якщо
її функцiя розподiлу ймовiрностей має вигляд
f(x|A,B,n)=
(
A
x
)(
B
n−x
)
(
A+B
n
)
, коли x =0,1,2,...,n,
0, в iнших випадках.
(4.1.9)
Гiпергеомертичний розподiл можна отримати наступним чином. Нехай є
A + B предметiв, причому A предметiв мають тип 1, а B предметiв мають
тип 2. Припуститмо, що вибираються n предметiв з цiєї сукупностi без
208
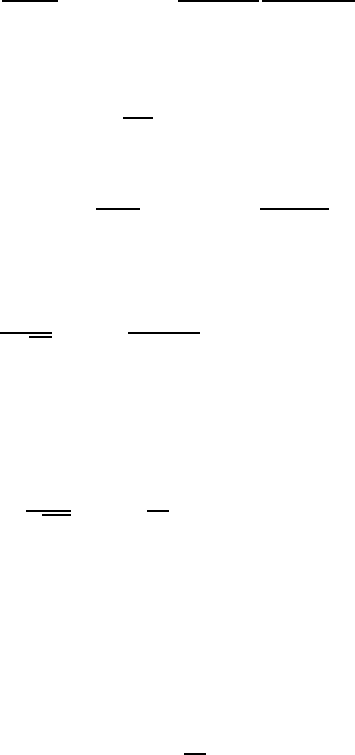
повернення. Нехай X позначає кiлькiсть предметiв типу 1 у цiй вибранiй
сукупностi предметiв. Тодi X має вказаний гiпергеомертичний розподiл.
Функцiя розподiлу ймовiрностей (4.1.9) вiдмiнна вiд нуля лише у тому
випадку, коли цiле число лежить в iнтервалi
max{0,n − B}≤x ≤ min{n,A}. (4.1.10)
Якщо випадкова величина X має гiпергеомертичний розподiл (4.1.9) з
параметрами A, B, n,то
E(X)=
nA
A + B
, Var(X)=
nAB
(A + B)
2
A + B − n
A + B − 1
. (4.1.11)
Рiвномiрний розподiл. Випадкова величина X має рiвномiрний роз-
подiл на iнтервалi (a,b),де−∞ <a<b<∞,якщовонамаєабсолютно
неперервну функцiю розподiлу зi щiльнiстю
f(x|a,b)=
1
b−a
, коли a<x<b,
0, в iнших випадках.
(4.1.12)
Якщо X має рiвномiрний розподiл iз щiльнiстю (4.1.12), то
E(X)=
a + b
2
, Var(X)=
(b − a)
2
12
. (4.1.13)
Нормальний розподiл. Випадкова величина X має нормальний роз-
подiл зсереднiмa та дисперсiєю σ
2
(−∞ <a<∞,σ>0),якщовона
має абсолютно неперервну функцiю розподiлу зi щiльнiстю
f(x|a,σ
2
)=
1
σ
√
2π
exp
−
(x − a)
2
2σ
2
, −∞<x<+∞. (4.1.14)
Якщо X має нормальний розподiл iз щiльнiстю (4.1.14), то
E(X)=a, Var (X)=σ
2
. (4.1.15)
Нормальний розподiл з середнiм a =0та дисперсiєю σ
2
=1назива-
ється стандартним нормальним розподiлом. Щiльнiсть такого розподiлу
має вигляд
f(x|0,1) =
1
√
2 π
exp
−
x
2
2
, −∞<x<+∞. (4.1.16)
Можна показати, що будь-яка лiнiйна комбiнацiя нормально розподiлених
випадкових величин має нормальний розподiл. Якщо, наприклад, випад-
ковi величини X
1
,X
2
,...,X
k
незалежнi i мають нормальний розподiл iз
середнiми a
i
та дисперсiями σ
2
i
,тосумаb
1
X
1
+ b
2
X
2
+ ···+ b
k
X
k
випадко-
вих величин має нормальний розподiл з середнiм b
1
a
1
+ b
2
a
2
+ ···+ b
k
a
k
та дисперсiєю b
1
σ
2
1
+ b
2
σ
2
2
+ ···+ b
k
σ
2
k
.
Мiра точностi τ нормального розподiлу визначається як величина,
обернена до дисперсiї, тобто
τ =
1
σ
2
. (4.1.17)
209
Якщо X має нормальний розподiл з середнiм a та мiрою точностi τ,то
щiльнiсть такого розподiлу можна записати у виглядi
g(x|a,τ)=
!
τ
2 π
"
1/2
exp
−
τ(x − a)
2
2
. (4.1.18)
Гамма-розподiл. Випадкова величина X має гамма-розподiл зпара-
метрами α та β (α>0,β>0), якщо вона має абсолютно неперервну
функцiю розподiлу iз щiльнiстю
f(x|α,β)=
β
α
Γ(α)
x
α−1
e
−βx
, коли x ≥ 0,
0, в iнших випадках.
(4.1.19)
Гамма-функцiя Γ(α), яка входить у спiввiдношення (4.1.19), визначає-
ться наступним спiввiдношенням
Γ(α)=
∞
0
u
α−1
e
−u
du, α > 0. (4.1.20)
Гамма-функцiя Γ(α) функцiя має такi властивостi:
Γ(α)=(α − 1)Γ(α − 1),α > 1, Γ(1) = 1, Γ
1
2
=
√
π. (4.1.21)
Якщо випадкова величина X має гамма-розподiл iз щiльнiстю (4.1.19),
то
E(X)=
α
β
, Var(X)=
α
β
2
. (4.1.22)
У тому випадку, коли α =1,β>0, розподiл, що визначається щiльнi-
стю (4.1.19), називається експоненцiйним (показниковим) розподiлом з
параметром β.
Якщо n натуральне число, то гамма-розподiл з параметрами α = n/2 та
β =1/2 називається χ
2
(хi-квадрат) розподiлом з n ступенями вiльностi.
Якщо випадковi величини X
1
,X
2
,...,X
n
незалежнi i мають нормаль-
ний розподiл iз середнiми 0 та дисперсiями 1 (стандартний нормальний
розподiл), то сума X
2
1
+ X
2
2
+ ···+ X
2
n
має χ
2
–розподiл з n ступенями
вiльностi.
Iнша важлива властивiсть така. Нехай випадковi величини X
1
,X
2
,...,
X
n
незалежнi i мають нормальний розподiл iз середнiми a та дисперсiями
σ
2
.Нехай
X =
1
n
n
i=1
X
i
,S
2
=
1
σ
2
n
i=1
(X
i
− X)
2
.
Величина S
2
має χ
2
-розподiл з n − 1 ступенями вiльностi. При цьому
величини S
2
та X незалежнi.
210
