Моклячук М.П., Ямненко Р.Є. Лекції з теорії вибору та прийняття рішень (на укр. языке)

Подождите немного. Документ загружается.

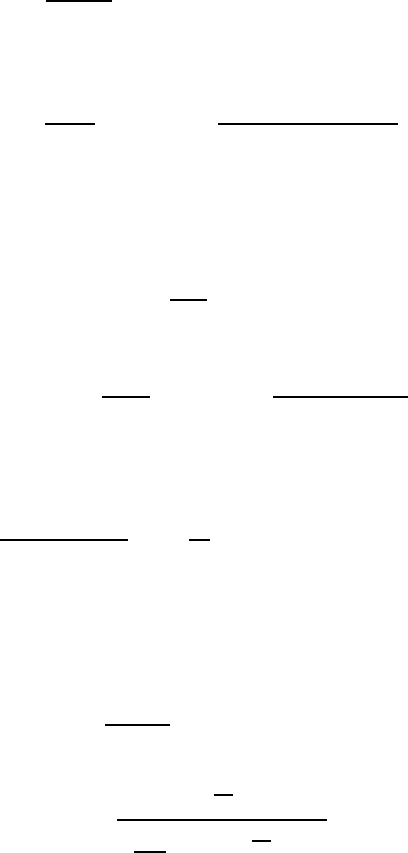
Бета-розподiл. Випадкова величина X має бета-розподiл зпараме-

трами α та β (α>0,β>0) , якщо вона має абсолютно неперервну

функцiю розподiлу iз щiльнiстю

f(x|α,β)=



Γ(α+β)

Γ(α)Γ(β)

α−1

(1 − x)

β−1

, коли 0 <x<1,

0, в iнших випадках.

(4.1.23)

де Γ(α) – це гамма-функцiя, що визначається згiдно з (4.1.20).

Якщо X має бета-розподiл iз щiльнiстю (4.1.23), то

E(X)=

α + β

, Var (X)=

αβ

(α + β)

(α + β +1)

. (4.1.24)

У тому випадку, коли α = β =1, бета-розподiл є рiвномiрним розподiлом

на iнтервалi (0,1).

Розподiл Парето. Випадкова величина X має розподiл Парето зпа-

раметрами x

та α (x

> 0,α>0), якщо вона має абсолютно неперервну

функцiю розподiлу iз щiльнiстю

f(x|x

,α)=



αx

α+1

, коли x>x

0, в iнших випадках.

(4.1.25)

Якщо X має розподiл Парето iз щiльнiстю (4.1.25), (α>2),то

E(X)=

αx

α − 1

, Var (X)=

αx

(α − 1)

(α − 2)

. (4.1.26)

Розподiл Стьюдента. Випадкова величина X має t-розподiл (розподiл

Стьюдента) з α ступенями вiльностi α>0) ,якщовонамаєабсолютно

неперервну функцiю розподiлу iз щiльнiстю

f(x|α)=

Γ((α +1)/2)

Γ(α/2)(απ)

1/2





−(α+1)/2

, −∞<x<∞. (4.1.27)

В багатьох статистичних задачах параметр α – це натуральне число.

У тому випадку, коли α =1, розподiл iз щiльнiстю (4.1.27) називають

розподiлом Кошi.

Важливiсть t-розподiлу в статистицi пояснюється такою властивiстю.

Якщо X та Y – незалежнi випадковi величини, причому X має стандар-

тний нормальний розподiл, а Y має χ

-розподiл з n ступенями вiльностi,

то випадкова величина

(Y/n)

1/2

має t-розподiл з n ступенями вiльностi. З

цiєї властивостi випливає, що для вибiрки X

,...,X

знормального

розподiлу з параметрами a, σ

випадкова величина

1/2

(X − a)



n−1



i=1

− X)



1/2

(4.1.28)

211

має t-розподiл з n − 1 ступенями вiльностi.

Якщо випадкова величина X має t-розподiл з α (α>2) ступенями

вiльностi iз щiльнiстю (4.1.27), то

E(X)=0, Var (X)=

α − 2

. (4.1.29)

Сiмейство t-розподiлiв можна розширити, якщо добавити всi щiльно-

стi, якi можна отримати зi щiльностi (4.1.27) за допомогою зсуву та пе-

ретворень масштабу. Говорять, що випадкова величина X має t-розподiл

з α ступенями вiльностi, параметром зсуву µ та мiрою точностi τ (α>

0, −∞<µ<∞,τ > 0), якщо щiльнiсть випадкової величини має вигляд

g(x|α,µ,τ)=

1/2

Γ((α +1)/2)

Γ(α/2)(απ)

α/2



τ(x − µ)



−(α+1)/2

. (4.1.30)

Зауважимо, що параметр τ , який тут названий мiрою точностi t-розподiлу,

не являється величиною, оберненою до дисперсiї розподiлу.

Мультиномiальний розподiл. Розглянемо експеримент, результати яко-

го належать одному з k, k ≥ 2,класiв.Нехайp



i=1

,позначаєймовiр-

нiсть того, що результат експерименту належить i-му класу, i =1,2 ...,k.

Припустимо, що експеримент проводиться раз i всi результати експери-

менту незалежнi. Нехай X

– це число результатiв, що належать i-му

класу. Тодi випадковий вектор X =(X

,...,X

) має мультиномiальний

розподiл з параметрами n та p =(p

,...,p

).Нехайx =(x

,...,x

) по-

значає точку з R

, кожна координата x

якої є невiд’ємним цiлим числом,

причому



i=1

= n.

Тодi в точцi x =(x

,...,x

) значення функцiї розподiлу ймовiрностей

випадкового вектора X =(X

,...,X

) дорiвнює

f(x|n,p)=

! ···x

···p

. (4.1.31)

Якщо випадковий вектор X =(X

,...,X

) має мультиномiальний розпо-

дiл з параметрами n та p =(p

,...,p

), то вектор середнiх (математичне

сподiвання) X матиме вигляд E(X)=n(p

,...,p

Var (X

)=np

(1 − p

),i=1,...,k;

Cov (X

)=−np

; i,j =1,...,k,i= j. (4.1.32)

Якщо випадковий вектор X =(X

,...,X

) має мультиномiальний розпо-

дiл з параметрами n та p =(p

,...,p

), то розподiл кожної компоненти X

є бiномiальним з параметрами n та p

212

Розподiл Дiрiхле.ВипадковийвекторX =(X

,...,X

) має розподiл

Дiрiхле з параметричним вектором α =(α

,...,α

), α

> 0, i =1,...,k,

якщо вiн має абсолютно неперервну функцiю розподiлу зi щiльнiстю

f(x|α)=







Γ(α

+···+α

Γ(α

)···Γ(α

)

−1

···x

−1

, коли x

> 0,



0, в iнших випадках.

(4.1.33)

Розподiл Дiрiхле називають ще багатовимiрним бета-розподiлом.

Якщо випадковий вектор X =(X

,...,X

) має розподiл Дiрiхле з

параметричним вектором α =(α

,...,α

),томоментиE(X

···X

),де

...,r

– невiд’ємнi цiлi числа, можна обчислити за формулою

E(X

···X





i=1



)

i=1

Γ(α

+ r

)

i=1

Γ(α

)Γ





i=1

(α

+ r

)



(4.1.34)

Зформуливипливає,що





i=1



E(X

, (4.1.35)

Var (X

(α

− α

)

(α

+1)

, (4.1.36)

Cov (X

)=−

(α

+1)

. (4.1.37)

4.2. СПРЯЖЕНI СIМЕЙСТВА РОЗПОДIЛIВ

Планування та аналiз експерименту виявляються досить нескладними,

якщо iснує стандартне сiмейство розподiлiв параметра W,щомаєтаку

властивiсть. Якщо апрiорний розподiл W належить цьому сiмейству, то

при будь-якому об’ємi вибiрки n i будь-яких значеннях спостережень у

вибiрцi апостерiорний розподiл W також належить цьому сiмейству. Сi-

мейство розподiлiв, що мають таку властивiсть, називається замкнутим

вiдносно процесу вибору. Його називають також спряженим сiмейством

розподiлiв через особливий зв’язок, який iснує мiж розподiлами параме-

тра i розподiлами спостережень.

Припустимо,наприклад,щоX

,...,X

–повторнавибiрказрозподiлу

Бернуллi з невiдомим значенням параметра W. Припустимо також, що

213

апрiорний розподiл W є бета-розподiл iз заданими значеннями параметрiв

α i β (α>0,β > 0). Тодi апрiорна щiльнiсть розподiлу ймовiрностей p

параметру W є

p (ω) ∝ ω

α−1

(1 − ω)

β−1

, 0 <ω<1. (4.2.1)

Тут ми вживаємо символ пропорцiйностi ∝, щоб вказати, що щiльнiсть

розподiлу p(ω) задається правою частиною (4.2.1) з точнiстю до множни-

ка, який не мiстить ω. Взагалi, якщо апрiорна щiльнiсть розподiлу W є

p(ω) i умовна щiльнiсть розподiлу при W = ω є f(·|ω),тоапостерiорна

щiльнiсть розподiлу ймовiрностей p (·|x) параметра W при X = x є

p (ω|x) ∝ p (ω) f (x|ω) ,ω∈ Ω. (4.2.2)

Вживання символу пропорцiйностi у спiввiдношеннi (4.2.2) законне, бо

умовна щiльнiсть розподiлу W дорiвнює правiй частини (4.2.2), подiленiй

на



Ω

f (x|ω



) p (ω



) dv (ω



куди w не входить.

Повернемося до нашого прикладу. Умовна сумiсна щiльнiсть розподiлу

(·|ω) вибiрки X

,...,X

при W = w дається рiвнiстю (??). Тому в силу

спiввiдношень (4.2.1), (4.2.2) апостерiорна щiльнiсть розподiлу ймовiрно-

стей p (·|x

,...,x

) параметра W при X

= x

,i =1,2,...,n є

p (w|x

,...x

) ∝ ω

α+y−1

(1 − ω)

β+n−y−1

. (4.2.3)

Тут y =



i=1

. Iз спiввiдношення (4.2.3) видно, що апостерiорний розподiл

W є бета-розподiл з параметрами α + y i β + n − y.Мидовелинаступну

теорему.

Теорема 4.2.1. Нехай X

,...,X

– повторна вибiрка з розподiлу Бер-

нуллi з невiдомим значенням параметра W . Припустимо, що апрiорний

розподiл W є бета-розподiл з параметрами α i β, α>0,β > 0.Тодi

апостерiорний розподiл W при X

= x

,i =1,2,...,n, є бета-розподiл з

параметрами α + y i β + n −y,деy =



i=1

. Iншими словами, сiмейство

бета-розподiлiв спряжене з сiмейством розподiлiв Бернуллi.

214

4.3. СПРЯЖЕНI СIМЕЙСТВА ДЛЯ ВИБIРОК З РIЗНИХ

СТАНДАРТНИХ РОЗПОДIЛIВ

У цьому параграфi ми вкажемо спряженi сiмейства розподiлiв для ви-

бiрок з розподiлу Пуассона, вiд’ємного бiномiального i показникового роз-

подiлiв.

Теорема 4.3.1. Нехай X

,...,X

— повторна вибiрка з розподiлу Пуас-

сона з невiдомим значенням середнього W . Припустимо, що апрiорний

розподiл W є гамма-розподiл з параметрами α i β, α>0, β>0.Тодi

апостерiорний розподiл W при X

= x

,i =1,2,...,n, є гамма-розподiл

зпараметрамиα +



i=1

, β + n.

Доведення. Нехай f

,...,x

|ω) позначає умовну щiльнiсть розподiлу

випадкових величин X

,...,X

iнехайp(ω) – апрiорна щiльнiсть розпо-

дiлу W. Якщо y =



i=1

, то з умов теореми випливає, що при w>0

,...,x

|ω) ∝ ω

−nω

, (4.3.1)

p (ω) ∝ ω

α−1

−βω

. (4.3.2)

Якщо p (ω|x

,...,x

) позначає апостерiорну щiльнiсть розподiлу W при

= x

(i =1,2,...,n),то

p (ω|x

,...,x

) ∝ f

,...,x

|ω) ξ (ω) . (4.3.3)

З (4.3.1)—(4.3.3) випливає, що

p (ω|x

,...,x

) ∝ ω

α+y−1

−(β+n)ω

. (4.3.4)

З (4.3.4) видно, що апостерiорна щiльнiсть розподiлу W єщiльнiсть

гамма-розподiлу з параметрами α + y i β + n.

Як мiра розсiювання розподiлу додатної випадкової величини часто

вживається коефiцiєнт варiацiї, який визначається спiввiдношенням

[Var(X)]

1/2

E(X)

, (4.3.5)

де

Var(X)=E{[X − E(X)]

Якщо випадкова величина X має гамма-розподiл з параметрами α i β то

E(X)=

, Var(X)=

. (4.3.6)

215

З цих спiввiдношень та теореми 4.3.1 випливає, що коефiцiєнт варiацiї

апостерiорного розподiлу W є



α +



i=1



−

. (4.3.7)

Нехай ε>0 – фiксоване число. Припустимо, що спостереження розпо-

дiлу Пуассона проводяться доти, поки коефiцiєнт варiацiї апостерiорного

розподiлу W не стане ≤ ε. Тодi вибiрку треба продовжувати до моменту

першого виконання нерiвностi

α +



i=1

≥

Наступнi теореми описують спряженi сiмейства розподiлiв для вибiрок

з вiд’ємного бiномiального та експоненцiйного (показникового) розподiлiв.

Доведення теорем аналогiчнi доведенню попередньої теореми 4.3.1.

Теорема 4.3.2. Нехай X

,...,X

– повторна вибiрка з вiд’ємного бiно-

мiального розподiлу з параметрами r i W ,деr фiксоване (r>0),а

значення W невiдоме. Нехай апрiорний розподiл W є бета-розподiл з

параметрами α, β, α>0, β>0. Тодi апостерiорний розподiл W при

= x

, i =1,2,...,n, є бета-розподiл з параметрами α+ rn i β +



i=1

Теорема 4.3.3. Нехай X

,...,X

– вибiрка з експоненцiйного розпо-

дiлу з невiдомим значенням параметра W . Нехай апрiорний розподiл

W є гамма-розподiл з параметрами α i β, α>0, β>0.Тодiапо-

стерiорний розподiл W при X

= x

, i =1,2,...,n), є гамма-розподiл з

параметрами α + n i β +



i=1

4.4. СПРЯЖЕНI СIМЕЙСТВА ДЛЯ ВИБIРОК З

НОРМАЛЬНОГО РОЗПОДIЛУ

Ми почнемо з розгляду нормальних розподiлiв з вiдомою мiрою точно-

стi, або, що те ж саме, з вiдомою дисперсiєю.

Теорема 4.4.1. Нехай X

,...,X

— повторна вибiрка з нормаль-

ного розподiлу з невiдомим значенням середнього W i заданою мiрою

точностi r (r>0). Припустимо, що апрiорний розподiл W нормальний

216

iз середнiм µ i мiрою точностi τ, −∞<µ<∞, τ>0.Тодiапостерi-

орний розподiл W при X

= x

(i =1,2,...,n) нормальний iз середнiм µ



i мiрою точностi τ + nr,де



τµ+ nr¯x

τ + nr

. (4.4.1)

Доведення. При −∞ <ω<∞ щiльнiсть розподiлу f

,...,x

|ω) ви-

падкових величин X

,...,X

задовольняє умовi

,...,x

|ω) ∝ exp

−



i=1

− ω)

. (4.4.2)

Але



i=1

− ω)

= n (ω − ¯x)



i=1

− ¯x)

. (4.4.3)

Оскiльки останнiй член рiвностi (4.4.3) не мiстить ω, то ми можемо пере-

писати спiввiдношення (4.4.2) так:

,...,x

|ω) ∝ exp

−

(ω − ¯x)

. (4.4.4)

Апрiорна щiльнiсть розподiлу p (ω) параметра W задовольняє умовi

p (ω) ∝ exp

−

(ω − µ)

. (4.4.5)

Апостерiорна щiльнiсть розподiлу p (ω|x

,...,x

) параметра W пропор-

цiйна добутку функцiй, що фiгурують у (4.4.4) i (4.4.5). Легко показати,

що

τ (ω − µ)

+ nr (ω − ¯x)

= τ + nr (ω − µ



)

τnr(¯x − µ)

τ + nr

. (4.4.6)

Оскiльки останнiй член у (4.4.6) не мiстить ω, вiн може бути включений

у нормуючий множник, i ми одержуємо спiввiдношення

p (ω|x

,...,x

) ∝ exp

−

τ + nr

(ω −µ



)

. (4.4.7)

Тут µ



задається спiввiдношенням (4.4.1). З (4.4.7) випливає, що апосте-

рiорний розподiл W нормальний iз середнiм µ



i мiрою точностi τ +nr.

Ця теорема показує, чому краще виражати нашi результати через мiру

точностi, а не через дисперсiю. Середнє µ



апостерiорного розподiлу W

можна записати у видi



τ + nr

¯x +

τ + nr

µ. (4.4.8)

Ми бачимо, що µ



–цезваженесереднє¯x i µ,де¯x – значення вибiр-

кового середнього, а µ — середнє апрiорного розподiлу W. Тому можна

217

розглядати середнє апостерiорного розподiлу, як зважене середнє оцiнки

W, побудованої по вибiрцi, i оцiнки параметра W, одержаної виходячи з

апрiорного розподiлу. Ваги оцiнок, ¯x i µ, у цьому усередненнi пропорцiйнi

nr i τ,деnr – мiра точностi умовного розподiлу вибiркового середнього

при будь-якому фiксованому значеннi W, а τ – мiра точностi апрiорного

розподiлу W. Чим бiльше обсяг вибiрки n i чим вище точнiсть r кожного

спостереження, тим бiльше вага, що дається ¯x.

Вигляд мiри точностi апостерiорного розподiлу W досить простий. То-

чнiсть зростає на r одиниць при кожному спостереженнi незалежно вiд

одержаних значень спостережень. Тому при збiльшеннi числа спостере-

жень розподiл W усе бiльш концентрується бiля його середнього, у той

час як значення середнього залежать вiд спостережень.

У наступнiй теоремi розглядаємо нормальний розподiл, для якого зна-

чення середнього задане, а значення мiри точностi невiдоме.

Теорема 4.4.2. Нехай X

,...,X

– повторна вибiрка з нормального

розподiлу з заданим значенням середнього m i невiдомим значенням

мiри точностi W , i нехай апрiорний розподiл W є гамма-розподiл з

параметрами α, β, α>0, β>0. Тодi апостерiорний розподiл W при

= x

,i =1,2,...,n, є гамма-розподiл з параметрами α +

i β



= β +



i=1

− m)

. (4.4.9)

Для гамма-розподiлу з параметрами α i β коефiцiєнт варiацiї дорiвнює

−

. З теореми випливає, що коефiцiєнт варiацiї апостерiорного розподiлу

W спадає, коли обсяг вибiрки зростає.

Розглянемо тепер вибiрку з нормального розподiлу у якого середнє i

мiра точностi невiдомi. Спряженим сiмейством у цiй задачi має бути деяке

сiмейство двовимiрних розподiлiв.

Теорема 4.4.3. Нехай X

,...,X

– повторна вибiрка з нормального

розподiлу iз невiдомим значенням середнього M та невiдомим значе-

нням мiри точностi R. Нехай апрiорний сумiсний розподiл M та R

такий: умовний розподiл M при R = r (r>0) – нормальний iз се-

реднiм µ i мiрою точностi τr, −∞ <µ<∞, τ>0, а розподiл R є

гамма-розподiл з параметрами α i β, α>0, β>0. Тодi апостерiорний

сумiсний розподiл M та R при X

= x

, i =1,2,...,n, має наступний

вигляд: умовний розподiл M при R = r – нормальний iз середнiм µ



мiрою точностi (τ + n) r,де



τµ+ n¯x

τ + n

(4.4.10)

218

а розподiл R є гамма-розподiл з параметрами α +

i β



,де



= β +



i=1

− ¯x)

τn(¯x − µ)

2(τ + n)

. (4.4.11)

Доведення. При −∞ <m<∞, i r>0 нехай щiльнiсть розподiлу

,...,x

|m,r) випадкових величин X

,...,X

iнехайp(m,r) по-

значає щiльнiсть розподiлу ймовiрностей M та R. Тодi

,...,x

|m,r) ∝ r

exp

−



i=1

− m)

(4.4.12)

p (m,r) ∝ r

exp

−

τr

(m + µ)

α−1

−rβ

. (4.4.13)

Апостерiорна щiльнiсть розподiлу p (m,r|x

,...,x

) параметрiв M та R

пропорцiйна добутку правих частин спiввiдношень (4.4.12) i (4.4.13). З

рiвностей (4.4.3) i (4.4.6) випливає, що ця щiльнiсть розподiлу може бути

задана спiввiдношенням

p (m,r|x

,...,x

) ∝

∝



exp

−

(τ + n) r

(m − µ



)

$

α+

−1

−rβ



. (4.4.14)

Тут µ



визначається рiвнiстю (4.4.10), β



– рiвнiстю (4.4.11).

Функцiя у фiгурних дужках у спiввiдношеннi (4.4.14), як функцiя вiд

m, повинна бути пропорцiйна умовнiй щiльнiсть розподiлу M при вiдомо-

му R тому що змiнна m не входить у вираз в круглих дужках праворуч.

Але для кожного фiксованого значення r функцiя у фiгурних дужках

пропорцiйна щiльнiсть нормального розподiлу середнє значення i мiра то-

чностi якого заданi в умовах теореми. Звiдси випливає, що функцiя, що

стоїть в круглих дужках, повинна бути пропорцiйною щiльностi розпо-

дiлу R. Тому розподiл R є гамма-розподiл, параметри якого зазначенi у

теоремi.

Якщо сумiсна щiльнiсть розподiлу ξ параметрiв M та R –цещiльнiсть

нормального–гама розподiлу, що задається спiввiдношенням (4.4.13), то

умовний розподiл M для будь-якого заданого значення R = r буде нор-

мальним, але розподiл M таким не буде. Щiльнiсть розподiлу p

(m)

параметра M визначається рiвнiстю

(m)=

∞



p (m,r) dr, −∞<m<∞. (4.4.15)

219

Якщо скористатись символом пропорцiйностi i пропустити всi множники,

що не мiстять m, то з (4.4.13) одержимо, що p

(m) має наступний вигляд:

(m) ∝

β +

(m − µ)

−

2α+1

, (4.4.16)

чи

(m) ∝

2α

ατ (m − µ)

−

2α+1

. (4.4.17)

Порiвнюючи функцiю, що задається спiввiдношенням (4.4.16), з щiль-

нiстю t – розподiлу, бачимо, що розподiл M є t-розподiлом з 2α ступенями

вiльностi, параметром змiщення µ i мiрою точностi

ατ

. Апостерiорний роз-

подiл M знаходимо замiною µ, τ , α, β, їхнiми апостерiорними значеннями,

якi вказанi в теоремi. Отже, число ступенiв вiльностi 2α+ n апостерiорно-

го розподiлу не залежить вiд значень x

,...,x

, проте параметр змiщення

i точнiсть апостерiорного розподiлу вiд них залежать.

4.5. ВИБIРКА З РIВНОМIРНОГО РОЗПОДIЛУ

У цьому параграфi ми опишемо спряженi сiмейства розподiлiв для ви-

бiрок з рiвномiрного розподiлу з невiдомими значеннями однiєї чи обох

крайнiх точок.

Теорема 4.5.1. Нехай X

,...,X

– повторна вибiрка з рiвномiрного

розподiлу на iнтервалi (0,W ),дезначенняW невiдомо. Припустимо,

що апрiорний розподiл W – це розподiл Парето з параметрами ω

i α,

> 0, α>0. Тодi апостерiорний розподiл W npu X

= x

, i =1,2,...,n

є розподiлом Парето з параметрами ω



i α + n,де



=max{ω

,...,x

}. (4.5.1)

Доведення. При ω>ω

апрiорна щiльнiсть розподiлу p(ω) параметра W

має вигляд

p (ω) ∝

α+1

, (4.5.2)

оскiльки щiльнiсть розподiлу Парето з параметрами ω

i α, ω

> 0, α>0,

має вигляд

p (ω|ω

,α)=



αω

α+1

, при ω>ω

0, в iнших випадках.

(4.5.3)

Щiльнiсть розподiлу f

,...,x

|ω) задається рiвнiстю (??). Звiдси ви-

пливає, що апостерiорна щiльнiсть розподiлу p (ω|x

,...,x

) параметра

220